Scuola Politecnica e delle Scienze di Base
Corso di Laurea in Ingegneria Informatica
Elaborato finale in Misure per l’automazione e la produzione Industriale
Caratterizzazione di ADC in condizioni non
stazionarie
Anno Accademico 2015/2016
Candidato:
Alessandro Schiano
matr. N46001657
“ Il timore del Signore è il principio
della scienza ...Affida al Signore
le tue opere ,e i tuoi progetti
avranno successo... il Signore
infatti dà la saggezza; dalla sua
bocca provengono la scienza e
l'intelligenza. ”
Indice
Caratterizzazione di ADC in condizioni non stazionarie ......................................................................I
Indice .............................................................................................................................................. III
Introduzione ..................................................................................................................................... 4
Capitolo 1: Convertitore A/D ........................................................................................................... 5
1.1 Conversione ........................................................................................................................... 5
1.1.1 Campionamento ............................................................................................................... 6
1.1.2 Quantizzazione ................................................................................................................. 7
Capitolo 2: Caratterizzazione ADC ............................................................................................... 10
2.1 Caratterizzazione statica ...................................................................................................... 10
2.2 Caratterizzazione dinamica .................................................................................................. 12
2.2.1 Valutazione degli errori ................................................................................................. 15
Capitolo 3: Caratterizzazione ADC in condizioni non stazionarie ................................................ 19
3.1 Test con segnale modulato in frequenza .............................................................................. 21
Conclusioni .................................................................................................................................... 23
Bibliografia .................................................................................................................................... 24
Introduzione
La rapida evoluzione tecnologica dei computer e dei microprocessori, accompagnata
parallelamente da alcuni significativi progressi teorici nel campo della teoria dei segnali
(si pensi, ad esempio, agli algoritmi Fast Fourier Transform, FFT), ha determinato già da
numerosi anni la transizione dalle tecniche analogiche di elaborazione dei segnali verso
quelle digitali o numeriche.
I sistemi di misura numerici basano il proprio funzionamento su dispositivi elettronici che
effettuano la conversione analogico-digitale del segnale di interesse, operazione che
implica una discretizzazione del segnale sia nel tempo che nell’ampiezza. I dispositivi
preposti alla conversione analogico-digitale (A/D) sono i convertitori A/D.
Al fine di valutare le prestazioni della strumentazione numerica, risulta pertanto
interessante caratterizzare il comportamento dei convertitori A/D dal punto di vista
metrologico. La Norma attualmente vigente e preposta alla definizione delle procedure di
caratterizzazione dei convertitori A/D è la Norma IEEE 1241-2000 .
In questo lavoro di tesi si cerca di definire ed analizzare analiticamente le procedure di
caratterizzazione proposte dalla suddetta norma, caratterizzando il convertitore A/D anche
in condizioni non stazionarie.
4
Capitolo 1: Convertitore A/D
In molti casi i segnali da elaborare sono per loro natura analogici (si pensi, ad esempio,
alla voce umana, al suono generato da uno strumento musicale, ad un’immagine in bianco
e nero oppure a colori). In questi casi, per poter sfruttare a pieno i vantaggi offerti dalle
tecniche di elaborazione numerica, i segnali analogici debbono essere preventivamente
convertiti in segnali digitali. Dopo aver effettuato in digitale l’elaborazione desiderata, il
segnale digitale ottenuto è riconvertito nuovamente in un segnale analogico. Il circuito di
conversione analogico digitale o ADC (Analog to Digital Converter) ha quindi il compito
di eseguire questa conversione trasformando un segnale analogico in un segnale numerico.
1.1 Conversione
Figura 1.1
Da un punto di vista concettuale, la conversione A/D si compone di due operazioni distinte
(rappresentate schematicamente in fig. 1.1):
campionamento ;
quantizzazione;
5
1.1.1 Campionamento
La fase di campionamento consiste nel convertire un segnale analogico xa(t), che si
intende elaborare, in un segnale TD x(n)=xa(nTc), ottenuto prelevando da xa(t) i suoi
campioni equispaziati nel tempo di una prefissata quantità Tc ,dove Tc è detto periodo o
passo di campionamento, e il suo reciproco fc = 1/Tc è la frequenza di campionamento.
Figura 1.2
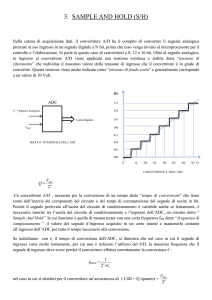
Nella realtà i convertitori oltre a campionare il segnale (fase Sample) necessitano che il
valore del campione si mantenga costante per un certo periodo di tempo (fase Hold) in
quanto essi hanno bisogno di un certo tempo per effettuare la conversione (tempo di
conversione).
Senza imporre alcun vincolo la sequenza x(n) non consente di determinare univocamente
il segnale analogico xa(t). Per convincersi di ciò, è sufficiente far riferimento alla fig. 1.3,
dove sono rappresentati due diversi segnali analogici xa,1(t) e xa,2(t), che assumono gli
stessi valori in tutti gli istanti di tempo che sono multipli interi di Tc, ossia
x(n) = xa,1(nTc) = xa,2(nTc), ∀n ∈ Z. Più in generale, assegnata una sequenza
x(n), in assenza di ulteriori vincoli, esistono infiniti segnali analogici che, campionati con
passo Tc, generano la sequenza x(n).
La perfetta ricostruzione di xa(t) a partire dalla sequenza x(n) può avvenire pertanto solo
se sono soddisfatte alcune condizioni aggiuntive.
6
Figura 1.3
Secondo il teorema di Shannon un segnale a banda rigorosamente limitata con banda
monolatera B =W è ricostruibile univocamente a partire dai suoi campioni solo se la
frequenza di campionamento fc = 1/Tc soddisfa la condizione di Nyquist:
fc ≥ 2W ;
Campionare in frequenza equivale a replicare nel tempo e viceversa campionare nel tempo
equivale a replicare in frequenza. Il segnale di partenza si ottiene quindi effettuando un’
operazione di filtraggio (mediante filtro passa-basso).
Nel caso in cui non sono soddisfatte le condizioni del teorema di Shannon si ottiene una
sovrapposizione degli spettri e quindi andando a filtrare al fine di ricostruire il segnale
analogico si va ad isolare un contenuto in frequenza che non e più appartenente al segnale
originale, ottenendo nel dominio del tempo un segnale diverso. Si verifica , cioè , il
cosiddetto fenomeno dell’ Aliasing.
1.1.2 Quantizzazione
Poichè xa(t) è un segnale ad ampiezza continua, il codominio del segnale TD x(n) ottenuto
a valle del campionamento è generalmente un sottoinsieme continuo di R, per cui x(n) non
è ancora un segnale digitale. A partire da x(n), l’operazione di quantizzazione consente di
ottenere un segnale TD xq(n) che può assumere solo un numero finito di possibili valori
(quindi un vero e proprio segnale digitale).
Il processo di trasformazione dei campioni in forma digitale implica necessariamente delle
approssimazioni legate al fatto che il numero di uscite possibili è di numero finito ed è
legato al numero di bit associati ad ogni campione. Dovendo codificare ciascun campione
7
con un numero limitato di bit, anche le possibili combinazioni binarie per la codifica sono
limitate. Questo significa in pratica, che con n bit le possibili combinazioni sono 2 che
definiscono i livelli di quantizzazione =2 .
Per quanto riguarda la dinamica di ingresso per un convertitore, indicata con
la
tensione di fondo scala, essa determina la dinamica di ingresso per il segnale, cioè la
massima ampiezza ammessa per il segnale da convertire.
I 2 livelli di quantizzazione suddividono l’intera dinamica di ingresso in altrettanti 2
intervalli più piccoli che hanno un’ampiezza pari a Q che chiamiamo quanto. Idealmente
V
l’ampiezza del quanto sarà: Q FSN . A questo punto è possibile associare a ciascun
2
livello di quantizzazione una tensione espressa in volt. Al livello N-1 associo la tensione
( −1) Volt con N livelli ed in particolare avrò che
=
.
La caratteristica più importante di un circuito di quantizzazione è la sua
transcaratteristica, che ne determina le prestazioni e le eventuali inefficienze. Essa è
definita come quella funzione che associa ad ogni livello di tensione assunto dalla tensione
analogica, in ingresso all’ADC, in un certo intervallo di tenuta , un’opportuna tensione v0
appartenente ad un insieme finito di valori. La transcaratteristica di un quantizzatore si
presenta come una curva costante a tratti (Figura 1.4).
Figura 1.4
Figura 1.5
8
La caratteristica di trasferimento non può essere invertita in modo da riottenere i valori di
tensione di ingresso per ogni valore digitale in uscita in quanto non esprime una
corrispondenza biunivoca tra ingresso e uscita. Per ottenerne tuttavia una stima
approssimata, bisogna considerare un’incertezza introdotta dal convertitore durante questa
fase. L’errore di quantizzazione è l’errore che il convertitore introduce nel processo di
digitalizzazione di un segnale di tensione in ingresso. Esso quindi è un contributo d’errore
intrinseco al processo di quantizzazione che non dipende dalla non idealità del dispositivo.
In presenza di un segnale d’ingresso costante Vin , l’errore di quantizzazione viene
definito come : Errore di quantizzazione codice Q Vin
L’andamento dell’errore di quantizzazione al variare della tensione assume la forma detta
a “Dente di sega” come in figura 1.5.
9
Capitolo 2: Caratterizzazione ADC
Caratterizzare un convertitore significa individuare la sua caratteristica di trasferimento
(caratteristica ingresso uscita). Esistono 2 modalità di caratterizzazione :
statica: viene eseguita ponendo in ingresso tensioni continue e costanti;
dinamica: viene eseguita con forme d’onda variabili ma periodiche.
2.1 Caratterizzazione statica
Essendo noto che l’andamento della caratteristica di un ADC è costituito da una gradinata
in cui l’altezza del gradino è per definizione unitaria (passaggio da un codice al
successivo), l’individuazione della caratteristica di trasferimento si riduce ad individuare i
valori della tensione di ingresso in corrispondenza dei quali si verificano le transizioni tra i
vari codici. Tali tensioni sono dette soglie di transizione. In particolare, con il simbolo Tk
si intende la tensione di ingresso che produce la transizione tra il codice k-1 e il codice k.
Per trovare sperimentalmente le soglie di transizione, la Norma suggerisce di ricorrere alla
teoria della probabilità e in tal senso definisce la soglia di transizione Tk come quel valore
di tensione per il quale il convertitore produce con la stessa probabilità il codice k e il
codice k-1. Per valutare tale probabilità si genera la tensione di prova continua, stabile e
calibrata, si fissa un valore iniziale della tensione di prova, si esegue un numero cospicuo
di conversioni, si conta il numero di occorrenza dei codici ottenuti, si ripete l’esperimento
variando la tensione di prova finché non si verifica che il 50% dei codici acquisiti è uguale
a k e il rimanente 50% è uguale a k-1. Avendo eseguito un numero cospicuo di conversioni
è possibile ritenere che la frequenza statistica di occorrenza dei codici approssima
abbastanza bene la loro probabilità di occorrenza. In realtà non si arriverà mai al 50%
10
essendo il quanto non ideale. Ad esempio se consideriamo la situazione descritta in fig 2.1
vediamo che la risoluzione è tale da non farmi prendere il giusto valore.
Figura 2.1
Figura 2.2
Per determinare la tensione di soglia si procede interpolando il punto 1 e 2 e piochè tra 2
punti passa 1 sola retta (figura 2.2) e indicato con p1 la probabilità di v1 e con p2
la probabilità di v2 possiamo considerare :
p50 p1 Tk v1
50% 43% Tk v1
v 2 v1
64% 43% v 2 v1
p 2 p1
Tk (v 2 v1) *
50 43
v1
64 43
Vantaggio: metodo semplice che permette di stimare quanto valgono i quanti reali
attraverso la relazione:
w[k]=T[k+1]-T[k];
Svantaggio: all’ aumentare del numero di bit il procedimento diventa lento ed è
richiesta una maggiore risoluzione al generatore di tensione; inoltre se ci sono
problemi di natura dinamica essi non vengono rilevati.
11
2.2 Caratterizzazione dinamica
Per la caratterizzazione dinamica, differentemente da quella statica, non è più possibile
utilizzare una tensione di prova continua e stabile per ottenere, come proposto dalla
Norma 1243-2010, la tensione di soglia per vari livelli di quantizzazione attraverso
un’analisi statistica. Almeno in linea di principio, una rampa lineare variabile dal fondo
scala negativo a quello positivo del convertitore in prova (rampa a fondo scala)
rappresenta una buona scelta come segnale di prova per la caratterizzazione dinamica.
Si va a campionare con una certa frequenza fc tale rampa e per ogni valore del segnale di
ingresso si annota il codice che si ottiene. Idealmente ci si aspetta di ottenere un numero di
occorrenze costante per ogni codice. Supponendo poi M campioni, allora ogni codice avrà
N occorrenze dove:
N
M
2n
Tuttavia, dato che i quanti non sono ideali, otterremo un distinto numero di occorrenze per
ogni codice. In particolare essi diminuiranno in relazione all’aumento della pendenza della
rampa per ogni quanto, ottenendo meno campioni per un codice.
Per ovviare a questo problema dovrei considerare un segnale “a dente di sega” in modo da
rendere periodico il segnale rampa e poter quindi prelevare un adeguato numero di
campioni. Esso però è difficile da generare a causa dell’alto contenuto spettrale. Inoltre la
rampa ideale non esiste.
Adesso il problema è la scelta di un segnale di prova che riusciamo a gestire nel miglior
modo possibile. La Norma IEEE 1241-2000 propone l’uso di una sinusoide a fondo scala,
dove eventuali problemi di deformazione saranno corretti con un opportuno filtro a spillo.
In questo caso l’istogramma delle occorrenze non sarà uniforme, ma avrà una forma a U
poiché ci saranno più occorrenze dove la pendenza è minore (Figura 2.3)
12
Figura 2.3
Consideriamo mezzo periodo di sinusoide:
Figura 2.4
Analiticamente si ha :
2t
Vi FS cos
con T [0,T/2]
T
Supponendo di prendere N campioni distanziati tra loro di
soglia all’altra impiego un tempo τ:
=
dove
è il numero di occorrenze del codice
13
.
, allora per passare da una
Il k è dato dal valore che assume la funzione nel punto , ma esso è dato dalla somma di
tutti i τ che lo precedono e quindi :
= 0
+ 1
+⋯+
−1
Ovvero è uguale alla somma delle occorrenze di tutti i codici per Tc (Istogramma
cumulativo di tutti i codici).
T
T ho preso N campioni distanziati di
allora
è uguale a
2
2
dove N è il numero totale di campioni acquisiti nell’arco [0;π] e quindi:
Sapendo inoltre che in
d1
NTc
H [k 1]
Tk FS cos
N
Questa formula quindi permette di trovare le varie soglie.
Devo assicurare un
tale da avere almeno un campione per ogni codice, quindi se riesco
a campionare il segnale passante per lo zero avrò sicuramente almeno un campione anche
per i successivi, e per farlo devo campionare per un tempo tale che il salto di tensione sia
inferiore a un quanto:
V
Q FS
cos2f x Tc
2
2
Poiché siamo per ipotesi nell’intorno dello zero, il coseno ha andamento lineare, quindi:
T
FS
cos2f x Tc FS c
2
Tx
Successivamente:
T
Q
FS
Q n Fs c
2
Tx
2
14
dove
Tc
1
Tx N pp
e quindi dobbiamo campionare in modo da avere
N pp 2 n .
Tuttavia non è detto che questi campioni debbano essere presi in un unico periodo,
perché se così fosse non farei lavorare bene il convertitore, quindi bisogna prendere
questi campioni in più periodi rispettando la seguente relazione:
=
Dove N ed M devono essere coprimi (senza fattori comuni) tra loro, altrimenti
prenderei N campioni che si ripetono a blocchi di
N
.
M
2.2.1 Valutazione degli errori
A questo punto l’ analisi sperimentale per la caratterizzazione del dispositivo è terminata e
non resta altro che valutare i vari errori . Per fare ciò si riporta su di un piano cartesiano
l’andamento delle Tk reali in funzione delle Tki ideali. Interpolando linearmente questi
punti si ottengono i parametri m ed n della retta di equazione:
Y mX n
In cui m rappresenta l’errore di guadagno ed n l’errore di offset. Per trovare gli errori di
non linearità integrale e differenziale bisognerà innanzitutto calcolare i valori delle soglie
di transizione compensate Tkc (ossia depurate dagli errori di offset e guadagno) usando la
seguente espressione:
Tkc
Tk n
m
L’ errore di non linearità integrale stima la differenza verticale tra la caratteristica reale e
quella ideale. Esso è dato da :
INL (k )
(Tkc Tki )100
VFS
15
L’errore di non linearità differenziale, ci dice se una certa pedata è maggiore o minore di
Q. Quindi ci dà delle informazioni locali, in un certo punto della caratteristica. Quindi
ci dice la larghezza di una pedata di quanto si scosta da Q.:
DNL (k )
(Tk 1 Tk ) Q
Q
dove:
Q il valore nominale del quanto (errore di quantizzazione del convertitore ideale)
Tk+1 la soglia di transizione tra il codice k e il codice k+1;
TK la soglia di transizione tra il codice k-1 e il codice k;
Tkc la soglia di transizione compensata del convertitore in prova tra il codice k e il
codice k+1;
Tki la soglia di transizione del convertitore ideale tra il codice k e il codice k+1
Le relazioni sopra definite forniscono un’informazione di dettaglio che normalmente non
viene riportata sui manuali dove, invece , vengono riportati solo i valori per il worst case:
=
( )
DNL RMS [ DNL ( K )]
Nei
passaggi
precedenti
abbiamo
ipotizzato
1
N
N
DNL
2
(k )
i 1
un
andamento
monotono
della
transcaratteristica , cioè a codici che aumentano corrispondono tensioni che aumentano
evitando, in questo modo, il possibile problema derivante dal fatto che, data l’eventuale
presenza di tratti non consecutivi della caratteristica, sarebbero potuti essere prodotti
codici uguali. Ciò significa che quando si vanno a contare le occorrenze si troverà per un
certo codice un numero di occorrenze molto più alto rispetto agli altri, quindi si deve
andare ad usare un istogramma perché valutare le occorrenze non basta più.
Quindi i ragionamenti fatti precedentemente non sono più validi dato che nella realtà il
convertitore avrà errori di non monotonicità.
Nasce, dunque, la necessità di identificare nuovi parametri di valutazione per
caratterizzare il comportamento dell’ADC.
16
Uno dei parametri principali è l’ENOB, capace di valutare il numero di bit effettivi del
convertitore permettendoci di avere informazioni riguardo il comportamento dell’ADC.
La prima cosa che occorre fare è chiederci a valle di un processo di conversione quanti bit
sono corretti.
Nel caso di convertitore ideale di risoluzione Q, l’errore di quantizzazione introduce un
rumore, detto rumore di quantizzazione che risulta essere una variabile aleatoria con valori
Q Q
tra ; .
2 2
Tuttavia nel caso dell’ADC reale si possono avere molti più errori, quindi è errato dire che
= *
, quindi per trovare i bit effettivi occorre definire un convertitore ideale
equivalente a quello in esame (reale), cioè che abbiano rumore di quantizzazione uguale.
Il rumore di quantizzazione è il valore efficace del segnale errore di quantizzazione:
RMS noise
1
Q
Q
2
Q
Q2
Q
1 V 3 2
2
(
V
)
dv
errore
Q
Q 3 Q
12
12
2
2
Per il convertitore reale dobbiamo trovare un RMSnoise appropriato.
Ipotizzando che esista un convertitore ideale che ha lo stesso RMSnoise di quello reale,
allora il numero di bit del convertitore ideale sarà uguale al numero di bit effettivi del
convertitore reale. Dunque, se fissiamo il fondo scala del convertitore ideale uguale al
fondo scala del convertitore reale, possiamo porre la seguente uguaglianza per calcolare
RMSnoise del convertitore reale con la condizione che:
RMSnoise,reale > RMSnoise,ideale →
>
Avendo lo stesso FS, il numero di bit dell’ADC reale è minore di quello ideale. Vediamo:
RMS noise,ideale
Q
12
FS
N log 2
RMS
12
noise 12
FS
2
n
con N numero di bit del convertitore.
Tuttavia il problema principale per trovare l’ENOB è proprio andare a trovare quanto vale
RMSnoise,reale. Per eseguire quest’ultima operazione, occorre conoscere il segnale di
ingresso. Noto il segnale lo si converte confrontando il segnale convertito con il segnale di
17
ingresso, ovvero si fa una differenza . Di questa differenza se ne fa il valore efficace
ricavando RMSnoise.
Come indicato nella Norma IEEE 1241-2000, si usa una sinusoide ed attraverso la
conversione del convertitore A/D avremo che:
RMS noise
1
M
M
(V
k 1
k
Vik ) 2
dove :
M è il numero di campioni di acquisizione,
Vk è l’insieme dei valori del segnale quantizzato in uscita dal convertitore reale A/D,
Vik rappresenta l’insieme dei valori dell’ingresso sinusoidale al convertitore ideale.
A questo punto si vuole sapere quanto vale
, ovvero il quanto riferito al convertitore
ideale corrispondente. Per farlo scriviamo come segue
RMS noise
FS
ENOB log 2
RMS
12
noise 12
Qeq
Il risultato ottenuto è di estrema importanza dato che, applicato ad un convertitore reale in
cui non si conosce a priori il numero di bit, si può ottenere il valore dell’ENOB.
18
Capitolo 3: Caratterizzazione ADC in condizioni non stazionarie
I metodi standard per il test dinamico dell’ADC sono il Single Tone Fit test e il Discrete
Fourier Transform Test. I tipici parametri di caratterizzazione dell’ADC sono l’ENOB, il
THD,il SNHR(Signal to Nonharmonic Ratio), SINAD (Single Noise And Distortion),
SFDR(Spurious Free Dynamic Range) e il MTD (Multitone Harmonic Distorsion).Di
seguito andiamo a identificare alcuni di questi parametri per il segnale onda
sinusoidale,ovvero il segnale previsto dalla norma per la caratterizzazione dell’ADC.
Il THD (Total Harmonic Distorsion) è la distorsione armonica totale, definita come il
rapporto tra il valore quadratico medio della somma delle prime componenti armoniche
del segnale di uscita e l’ampiezza del segnale ricostruito :
n
THD
U
i 1
2
i
U1
Il SINAD è definito come il rapporto tra il valore efficace del segnale di ingresso ed il
valore efficace totale del rumore di quantizzazione e di tutti i prodotti di distorsione dovuti
alle non idealità del dispositivo. Normalmente il SINAD diminuisce all’aumentare della
frequenza del segnale in rapporto alla frequenza di campionamento; ciò significa che, per
una fissata frequenza di campionamento, le prestazioni dell’ADC peggiorano
progressivamente all’aumentare della frequenza del segnale. La sua espressione è la
seguente:
1
SINAD
1
THD 2
2
SNHR
19
L’interdipendenza tra il SINAD e l’ENOB è data dalla seguente equazione:
SINAD=6,02ENOB+1,76(dB).
Il range dinamico dell’ADC testato può essere caratterizzato dal parametro SFDR che è
dato dalla seguente espressione:
SFDR
U1
UM
Per analizzare questi parametri sono richiesti dei test con tempi di esecuzione molto
lunghi. Per ridurre questi tempi è possibile utilizzare segnali AM, FM e QAM, che sono
frequentemente utilizzati per le comunicazioni e le comunicazioni radio ,in ingresso all’
ADC .
Le precedenti formule derivano dal caso in cui per il test viene utilizzato il segnale
sinusoidale .Per altri tipi di segnali è necessario compensare l'influenza di diversi fattori
di cresta(CF) e correggere l’ ENOB .
Quindi, tramite questa correzione otteniamo la seguente formula per il calcolo dell’ENOB:
ENOB
SINAD 1.76 20 log CF
6.02
Quindi il SINAD diventa:
SINAD=6.02ENOB+1.76-20logCF.
Dove il fattore di cresta CF si definisce come:
CF
Con
il valore di picco e
Vp
Veff
il valore efficace del segnale.
20
3.1 Test con segnale modulato in frequenza
Il principio della modulazione in frequenza consiste nella modulazione della frequenza
della portante secondo l’espressione n (t ) n 0 cos( m t ) dove Δω è la deviazione di
frequenza del segnale modulato e
m FM
è l’indice di modulazione . L’espressione
del segnale modulato in frequenza è la seguente:
u FM U n sin n t
sin m t
m
Gli indici di modulazione adatti per il testing dell’ADC sono 0.25,0.5 e 1. Quindi le
ampiezze di tutte le componenti spettrali sono minori rispetto a quella della portante.
Valutiamo il segnale nel dominio della frequenza e determiniamo il SINADFM :
U n2
SINAD FM
m
i km / 2 , k 1, 2..
U
k 1, 2..
2
km
U 2fi U n2
U
k 1, 2..
2
km
Gli altri parametri (THD, SFDR, SNHR) possono essere derivati similmente come il
SINADFM . Di seguito si riporta una tabella contenente i risultati di test sperimentali
effettuati mediante l’impiego del generatore SMIQ 03B - Rhode Schwarz
con un
segnale (sinusoidale) a frequenza 1MHz e un segnale FM con frequenza modulata 100kHz
e indici di modulazione scelti 0.25,0.5 e 1. Gli spetti sono mostrati nelle figure da 3.1 a 3.4
Figura 3.1
Figura 3.2
21
Figura 3.3
Figura 3.4
Table results with Sine Wave and Fm signals
In generale è confermato che i segnali multi-tone possono essere utilizzati per il testing
dell’ ADC in un più ampio range di frequenze con costi minori.
Poi si ha la risoluzione dei problemi riguardo al fatto che il segnale non copre
completamente il fondo scala(FS) dell’ADC test e infine lo spettro di frequenza di un
segnale FM può essere molto ampio .
Uno dei principali svantaggi di questa procedura di test è la complicata elaborazione del
segnale modulato nel dominio del tempo tramite l’uso di metodi di fitting poiché il segnale
conterrà un range di frequenze invece di un singolo tono.
22
Conclusioni
In questo lavoro di tesi è stata presentata la caratterizzazione statica e dinamica dei
convertitori analogico-digitali seguendo, in primo luogo, quanto stabilito dalla norma IEEE
1241-2010 . Tale norma uniforma le procedure per il test dei convertitori A/D, nonché le
figure di merito atte alla loro caratterizzazione metrologica mediante l’impiego di un
segnale sinusoidale.
E’ chiaro però che nella pratica occorre convertire segnali di ogni tipo e a tal scopo si
passati all’analisi di metodi non tradizionali per la caratterizzazione dei convertitori
facendo riferimento ai segnali modulati per i quali è necessaria una correzione tramite il
fattore di cresta.
23
Bibliografia
[1]
Annalisa Liccardo, Dispense del corso Misure per l’Automazione e la Produzione
Industriale, Università degli studi di Napoli Federico II
[2]
Giacinto Gelli e Francesco Verde, Segnali e sistemi, 2008, 488 pagine.
[3]
Josef Vedral, Pavel Fexa, Jakub Svatoš, FM and QAM Signals for ADC Testing ,
2007, 4 pagine.
[4]
IEEE-SA Standards Board, American National Standards Institute, IEEE Standard
for Terminology and Test Methods for Analog-to-Digital Converters, 127 pagine, 2011
24