Divido l'intero in 5 parti
Divido l'intero in 5 parti
uguali e prendo 2 parti.
uguali e prendo 2 parti. Mi
numeratore
Mi restano ancora 3 parti.
restano ancora 3 parti.
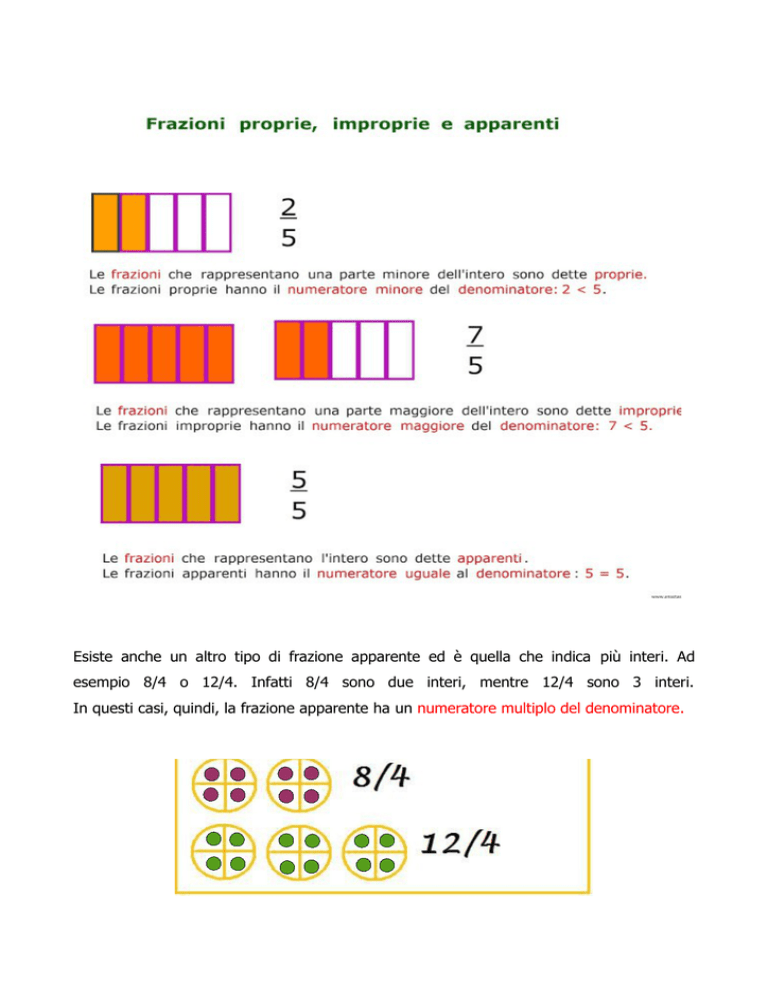
Esiste anche un altro tipo di frazione apparente ed è quella che indica più interi. Ad
esempio 8/4 o 12/4. Infatti 8/4 sono due interi, mentre 12/4 sono 3 interi.
In questi casi, quindi, la frazione apparente ha un numeratore multiplo del denominatore.
Altro esempio sulle frazioni equivalenti:
Data una frazione, come posso trovare una frazione ad essa equivalente?
Basta moltiplicare numeratore e denominatore per lo stesso numero.
Esempio:
devo trovare una frazione equivalente a
3
5
decido di moltiplicare numeratore e denominatore per 2:
3x2= 6
5x2
10
ho trovato una frazione equivalente a
3
5
avrei potuto moltiplicare numeratore e denominatore per 3, ottenendo:
3x3= 9
5x3
15
anche questa frazione è equivalente a
3
5
ADDIZIONI E SOTTRAZIONI TRA FRAZIONI CON DENOMINATORE DIVERSO
Prendiamo in considerazione la seguente addizione:
2
+
4
=
3
5
i denominatori delle frazioni sono diversi e sono numeri primi. Come opero?
1) Trovo il minimo comune multiplo tra i denominatori:
m.c.m. (5,3) = 5 x 3 = 15
(è sufficiente moltiplicare tra loro i due denominatori)
2) A destra del segno uguale traccio una linea di frazione e al posto del
denominatore scrivo 15:
2
+
4
=
15
3
5
3) Cosa scriverò al posto del numeratore? Devo svolgere le seguenti operazioni:
•
divido 15 per 5 e moltiplico il risultato della divisione per 2, ottengo 6 e lo scrivo a
numeratore;
•
ricopio il segno più;
•
divido 15 per 3 e moltiplico il risultato della divisione per 4, ottengo 20 e lo scrivo a
numeratore;
•
X
2
:
5
eseguo l'addizione e ottengo il risultato
+
4
3
=
6
+
15
20
=
26
15
Prendiamo in considerazione la seguente sottrazione:
3
4
-
=
2
7
i denominatori delle frazioni sono diversi e sono numeri primi. Come opero?
1) Trovo il minimo comune multiplo tra i denominatori:
m.c.m. (7,2) = 7 x 2 = 14
(è sufficiente moltiplicare tra loro i due denominatori)
2) A destra del segno uguale traccio una linea di frazione e al posto del
denominatore scrivo 14:
3
4
-
=
14
2
7
3) Cosa scriverò al posto del numeratore? Devo svolgere le seguenti operazioni:
•
divido 14 per 7 e moltiplico il risultato della divisione per 3, ottengo 6 e lo scrivo a
numeratore;
•
ricopio il segno meno;
•
divido 14 per 2 e moltiplico il risultato della divisione per 4, ottengo 28 e lo scrivo a
numeratore;
•
X
3
:
7
eseguo la sottrazione e ottengo il risultato
-
4
2
=
6
+
14
28
=
34
14
MOLTIPLICAZIONI E DIVISIONI TRA FRAZIONI
- Prendiamo in considerazione la seguente moltiplicazione tra frazioni:
4
x
2
=
3
5
Come opero?
•
Moltiplico i numeratori tra di loro;
•
moltiplico i denominatori tra di loro.
4
x
2
=
3
5
4x2
5x3
=
8
15
- Prendiamo in considerazione la seguente divisione tra frazioni:
5
:
4
=
9
2
Come opero?
•
Ricopio la prima frazione;
•
"trasformo" il segno della divisione in x;
•
riscrivo
la
seconda
frazione
invertendo
il
numeratore
denominatore.
5
2
x
9
=
4
adesso posso risolvere la moltiplicazione con la regola già enunciata.
con
il
Potenza di una frazione
Per elevare a potenza una frazione, dobbiamo elevare a quella potenza entrambi i
termini della frazione.
Esempi:
m.c.d. significa minimo comune
denominatore; per trovare il
m.c.d. si scompongono in fattori
primi i denominatori e si calcola
il minimo comune multiplo che
nel nostro esempio è 2 x 3 = 6;
trovato il m.c.d. si trasformano
le frazioni date in due frazioni
con lo stesso denominatore così
come indicato nell'esempio.
Tra due frazioni che hanno lo
stesso denominatore, la più
grande è quella con il
numeratore maggiore.










