Esercizi e complementi per gli insegnanti

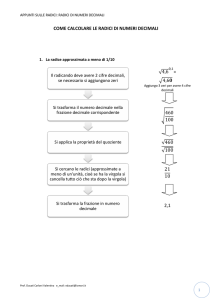
Esercizi e complementi
per gli insegnanti
II.e
Gli esercizi di questo paragrafo sono troppo difficili per essere assegnati ai bambini. Li proponiamo nella convinzione che possano
far riflettere gli adulti ed offrire spunti per attività guidate.
Lo schema nella pagina seguente è un diagramma
di Venn, in cui sono rappresentati gli insiemi dei
numeri di cui abbiamo parlato nel paragrafo I.c (i vari ambienti numerici). I numeri naturali sono all’interno, mentre le scritte numeri interi
negativi, numeri decimali limitati, numeri decimali illimitati periodici,
numeri decimali illimitati non periodici, corrispondono ai vari “anelli”.
I simboli N, Z, D, Q, R fanno riferimento agli insiemi a cui sono collegati da una freccia. Si faccia attenzione che, per questi simboli,
va preso in considerazione non un anello ma tutta la parte interna: ad
esempio, l’insieme Q dei numeri razionali contiene i naturali, gli interi
negativi, i decimali limitati e i decimali illimitati periodici. L’insieme
D rappresenta tutti i numeri decimali limitati, positivi e negativi, compresi gli interi.
Esercizio 1
46
numeri naturali
N
numeri interi negativi
Z
numeri decimali limitati (non interi)
D
numeri decimali illimitati periodici (con periodo non nullo)
Q
numeri decimali illimitati non periodici
R
Collocare nel diagramma di Venn i seguenti numeri:
0;
1,75;
4/3;
–6;
7/5;
CD
2.
Dove si trovano le frazioni decimali?
Esercizio 2
Quali delle seguenti frazioni sono equivalenti a frazioni decimali e, quindi, corrispondono a numeri
decimali limitati?
7/2;
1/3;
2/25;
21/14;
14/21;
99/60;
105/75.
a) Quali fra le seguenti scritture rappresentano lo
stesso numero?
1,8;
1,80;
1,08;
9/5;
27/15;
18/100
b) Indicare almeno quattro scritture che rappresentano uno stesso
numero decimale limitato.
Esercizio 3
Quante sono le frazioni equivalenti a 5/4? A quanti
numeri decimali limitati equivale la frazione 5/4
(escludendo scritture in cui l’ultima cifra decimale sia 0)?
Esercizio 4
47
In un contesto di misure approssimate, il simbolo
1,850 m ha un significato diverso da 1,85 m: infatti, nel primo caso si intende che il valore reale può discostarsi da
1,85 m per meno di un millimetro, mentre nel secondo caso facciamo implicitamente riferimento ad una approssimazione a meno di
un centimetro. Costruire e commentare esempi tratti dalla vita corrente.
Esercizio 5
L’insieme dei decimali limitati è denso, cioè fra due
numeri decimali ne è sempre compreso un altro.
Trovare un numero decimale compreso fra 2,9 e 3; trovare poi un numero decimale compreso fra 3 e 3,01. Quanti numeri naturali sono
compresi fra 4 e 5? e fra 4 e 14? Quanti numeri decimali limitati sono
compresi fra 4,7 e 4,8?
Esercizio 6
Consideriamo i numeri decimali con non più di
due cifre dopo la virgola (in termini di euro, si
tratta dei numeri che rappresentano somme di denaro che possiamo
formare con banconote e monete). L’insieme di questi numeri non è
denso, perché, ad esempio, non ci sono numeri con due cifre decimali compresi fra 3,75 e 3,76. In altre parole, nell’insieme dei numeri
considerati, il numero 3,76 è il più piccolo numero maggiore di
3,75. In tale insieme, qual è il più piccolo numero maggiore di 2,59?
e di 4,8? e di 7?
Nello stesso insieme, qual è il più grande numero minore di
2,01? e di 4,8? e di 7?
Esercizio 7
Nell’insieme N dei numeri naturali si può costruire una successione infinita di numeri che diventano sempre più grandi; ad esempio: 0 < 2 < 4 < 6 < … Nell’insieme N si può costruire una successione infinita di numeri che diventano sempre più piccoli? Nell’insieme Z dei numeri interi relativi
si può costruire una successione infinita di numeri che diventano
sempre più piccoli?
E nell’insieme dei numeri decimali limitati positivi, si può costruire una successione infinita di numeri che diventano sempre più
piccoli? (Ad esempio, si osservi che 1,1 > 1,01 > 1,001 > …).
Esercizio 8
48
Sia a un numero decimale con 2 cifre dopo la virgola e sia b un numero decimale con 3 cifre dopo
la virgola. Quante sono le cifre dopo la virgola di a + b e di a – b?
Più in generale, sia a un numero decimale con m cifre dopo la
virgola e sia b un numero decimale con n cifre dopo la virgola. Si verifichi che il numero delle cifre dopo la virgola di a + b e di a – b è
uguale, al massimo, al più grande fra m ed n. Si trovi poi un esempio
in cui a + b non è intero ma ha meno cifre dopo la virgola sia di a sia
di b. Se b è, invece, un numero intero, quante cifre dopo la virgola ha
a + b?
Esercizio 9
Sia a un numero decimale con m cifre dopo la virgola e sia b un numero decimale con n cifre dopo
la virgola. Si verifichi che il numero delle cifre dopo la virgola di a3b è
uguale, al massimo, alla somma fra m ed n (questa proprietà è più
chiara se si pensano a e b come frazioni decimali). Si trovino poi almeno due esempi di prodotti fra numeri decimali il cui risultato è un numero intero (ad esempio, 2,432,5 = …).
Per la divisione il discorso diviene complesso, come mostrano i
seguenti esempi:
12,5 : 4;
7 : 0,5;
6 : 2,5;
0,2 : 0,01;
10 : 3.
Considerando altri esempi ci si convince che, se il divisore è un numero intero, allora il quoziente ha almeno tante cifre decimali quante ne
ha il dividendo.
Esercizio 10
Siano a e b due numeri decimali limitati. È vero
che la loro media aritmetica (a + b)/2 è, a sua volta, un numero decimale limitato? Se a e b hanno al più due cifre decimali, quante cifre decimali ha al massimo la loro media aritmetica?
Trovare un caso in cui, pur non essendo interi né a né b, la media aritmetica è un numero naturale.
Esercizio 11
Siano a, b e c tre numeri decimali limitati. È vero
che la loro media aritmetica (a + b + c)/3 è sempre,
a sua volta, un numero decimale limitato?
Esercizio 12
49
Dopo aver calcolato il quoziente delle divisioni
5 : 0,1 = …;
5 : 0,01 = …;
5 : 0,001 = …
n
si stabilisca se il quoziente 5 : 0,1 aumenta o diminuisce al crescere di n.
Esercizio 13
Si considerino le potenze 0,51, 0,52, 0,53, 0,54, …
È vero che questi numeri diventano sempre più piccoli? Esiste un numero n tale che 0,5n sia più piccolo di un millesimo?
Esercizio 14
a) In base dieci si ha 1/4 = 0,25; pertanto, alla frazione 1/4 corrisponde un numero decimale limitato. Trovare una base B di numerazione posizionale nella quale la frazione un quarto abbia una rappresentazione con infinite cifre dopo la
virgola (cioè corrisponda a un numero illimitato periodico).
b) In base dieci si ha 1/3 = 0,333…; pertanto, alla frazione 1/3
corrisponde un numero decimale illimitato periodico. Trovare una base
B di numerazione posizionale nella quale la frazione un terzo abbia una
rappresentazione con un numero finito di cifre dopo la virgola.
c) È vero che per ogni frazione a/b esiste almeno una base B in
cui a/b ammette una rappresentazione con un numero finito di cifre
dopo la virgola?
Esercizio 15
1. 0 è un numero naturale e quindi va nella zona Risoluzioni di
centrale del diagramma; –6 va posto nell’anello alcuni dei
più interno, dove si trovano i numeri interi nega- precedenti
tivi. CD
2 va collocato nell’anello più esterno esercizi
(non si può esprimere con una frazione), mentre
4/3 nell’anello successivo procedendo verso l’interno (è un numero razionale ma non un decimale limitato). Infine 1,75 e 7/5 = 1,4 sono
numeri decimali limitati.
Le frazioni decimali corrispondono all’insieme D (numeri decimali limitati, e anche numeri naturali e numeri interi negativi).
2. Le frazioni equivalenti a frazioni decimali sono cinque: 7/2 = 35/10;
2/25 = 8/100; 21/14 = 15/10; 99/60 = 165/100; 105/75 = 14/10.
3. a) Si ha che 1,8 = 1,80 = 9/5 = 27/15.
50
4. Infinite frazioni (10/8, 15/12, ecc.); solo al numero 1,25.
6. Si può rispondere, ad esempio, 2,95 alla prima domanda e 3,005 alla seconda. Le risposte alle successive domande sono: nessuno; 9 (cioè i
numeri 5, 6, …, 13); infiniti (ad esempio 4,71; 4,711; ecc.).
7. 2,6; 4,81; 7,01; 2; 4,79; 6,99.
8. Non esiste in N una successione infinita di numeri che diventano
sempre più piccoli; invece, in Z si ha 0 > –1 > –2 > –3 > …
Esistono successioni infinite di numeri decimali limitati positivi
che diventano sempre più piccoli: oltre alla successione citata, si possono considerare ad esempio i numeri 3,5 > 3,45 > 3,445 > … In tali
successioni aumenta via via il numero delle cifre dopo la virgola.
9. Se m è maggiore di n, allora a + b ha sempre m cifre dopo la virgola:
ad esempio, 3,14 + 5,5 = 8,64. Se invece m = n, allora può capitare che
a + b abbia meno di m cifre dopo la virgola: ad esempio, se
a = 3,19 e b = 0,21, si ha a + b = 3,4. Se b è un numero intero, a + b
ha tante cifre dopo la virgola quante ne ha a.
10. Altri esempi di prodotti interi con fattori decimali sono:
7,531,2 = 9;
3,236,25 = 20.
11. La media aritmetica di due numeri decimali limitati è sempre un
numero decimale limitato; tuttavia, se a e b hanno due cifre decimali,
la loro media aritmetica ha di solito tre cifre decimali: ad esempio
(5,55 + 1,12)/2 = 3,335. In casi particolari, si ottengono meno cifre
decimali o addirittura numeri interi: ad esempio, se a = 3,8 e b = 6,2, la
loro media aritmetica è 5.
12. In generale, la media aritmetica di tre numeri decimali limitati
non è un numero decimale limitato. Ad esempio:
(3,1 + 2,2 + 1,4)/3 = 6,7/3 = 2,233…
13. Al crescere di n, il divisore 0,1n diminuisce e il quoziente 5 : 0,1n
aumenta.
51
14. Sì. Ad esempio, 0,5 10 = 0,00097… è più piccolo di un millesimo.
15. a) In base tre, la metà di 1 (un mezzo) si scrive 0,111… (con infinite cifre tutte uguali ad 1), mentre la metà della metà di 1 (un quarto)
si scrive 0,0202… (dopo la virgola, si alternano indefinitamente le cifre 0 e 2).
b) La cosa più semplice consiste nello scegliere come B proprio
tre: in tal caso, infatti, la scrittura 0,1 corrisponde ad un terzo.
c) Sì: basta, ad esempio, che la base B sia un multiplo di b.
52