AREA DEI POLIGONI 1
Area dei triangoli
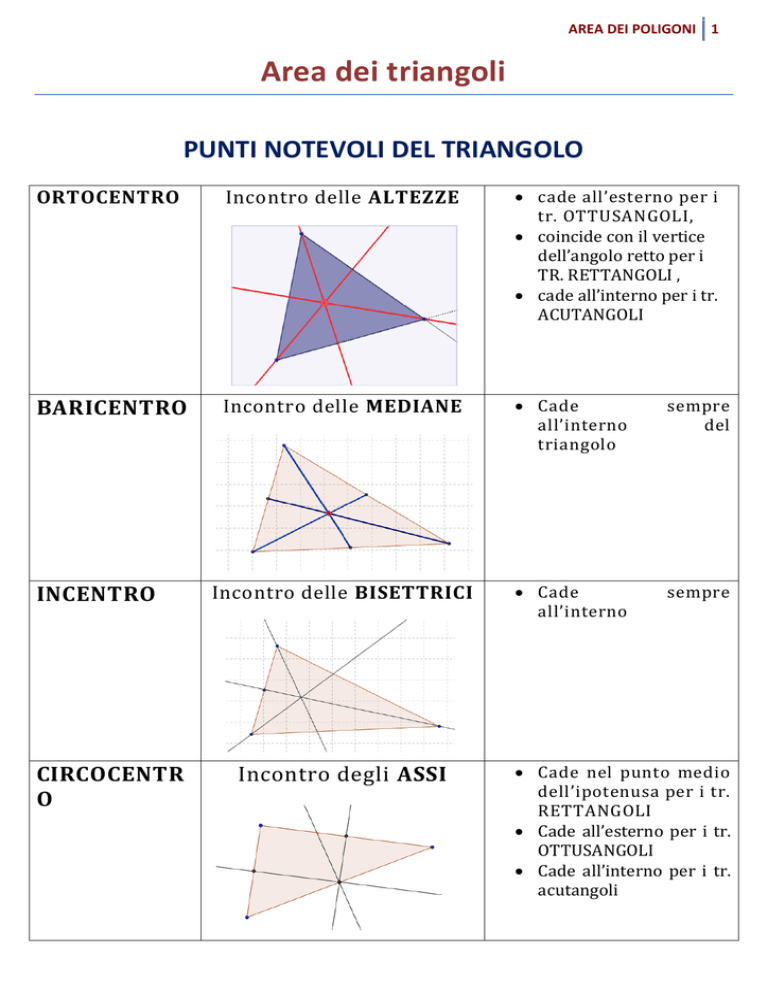
PUNTI NOTEVOLI DEL TRIANGOLO
ORTOCENTRO
Incontro delle ALTEZZE
cade all’esterno per i
tr. OTTUSANGOLI,
coincide con il vertice
dell’angolo retto per i
TR. RETTANGOLI ,
cade all’interno per i tr.
ACUTANGOLI
BARICENTRO
Incontro delle MEDIANE
Cade
all’interno
triangolo
sempre
del
Incontro delle BISETTRICI
Cade
all’interno
sempre
INCENTRO
CIRCOCENTR
O
Incontro degli ASSI
Cade nel punto medio
dell’ipotenusa per i tr.
RETTANGOLI
Cade all’esterno per i tr.
OTTUSANGOLI
Cade all’interno per i tr.
acutangoli
AREA DEI POLIGONI 2
Area del triangolo:
Un triangolo è equivalente alla metà di un parallelogrammo avente base e
altezza rispettivamente congruenti a quelle del triangolo.
L’area di un triangolo si ottiene moltiplicando la misura della base per quella
dell’altezza e dividendo per due il prodotto ottenuto:
𝑏∙ℎ
𝐴=
2
Formule inverse:
2∙𝐴
𝑏=
ℎ
2∙𝐴
ℎ=
𝑏
AREA DEI POLIGONI 3
CASO PARTICOLARE:
triangolo rettangolo
Raddopiando il triangolo rettangolo
𝐴𝐵𝐶 si ottiene un rettangolo AC’CB la cui
area misura:
𝐴𝑟𝑒𝑡𝑡𝑎𝑛𝑔𝑜𝑙𝑜 = 𝐴𝐶 ∙ 𝐵𝐶
L’area del triangolo ABC è la metà:
𝐴𝐶 ∙ 𝐵𝐶
𝐴𝐴𝐵𝐶 =
2
Dato che AC e BC sono i CATETI:
𝐴𝐴𝐵𝐶
Formule inverse:
2∙𝐴
𝑐1 =
𝑐2
𝑐1 ∙ 𝑐2
=
2
2∙𝐴
𝑐2 =
𝑐1
OSSERVAZIONE:
l’area del triangolo rettangolo può
essere calcolata come l’area di un
qualsiasi triangolo
𝐴𝐵 ∙ 𝐶𝐻
𝐴𝐴𝐵𝐶 =
2
Dalle due formule precedenti:
𝑐1 ∙𝑐2
𝑖∙ℎ
𝐴=
e 𝐴=
2
2
AREA DEI POLIGONI 4
Si ottiene la misura dell’altezza relativa all’ipotenusa:
𝑐1 ∙ 𝑐2
ℎ𝑖 =
𝑖
(cateto per cateto fratto ipotenusa)
Formula di Erone
È possibile calcolare l’area di un triangolo qualunque
conoscendo le misure dei suoi lati:
𝑝 =𝑎+𝑏+𝑐
𝑝
2
𝑝 𝑝
𝑝
𝑝
𝐴 = √ ∙ ( − 𝑎) ∙ ( − 𝑏) ∙ ( − 𝑐)
2 2
2
2
Esempio
Calcola l’area di un triangolo i cui lati misurano
rispettivamente 48 𝑐𝑚, 85 𝑐𝑚 e 91 𝑐𝑚.
Per risolverlo utilizzo la formula di Erone.
Serve il perimetro:
𝑝 = (48 + 85 + 91)𝑐𝑚 = 224 𝑐𝑚
Calcolo il semiperimetro:
𝑝
= 112 𝑐𝑚
2
AREA DEI POLIGONI 5
Applico la formula:
𝐴 = √112 ∙ (112 − 48) ∙ (112 − 85) ∙ (112 − 91)
= √112 ∙ 64 ∙ 27 ∙ 21 =
Si fa la scomposizione in fattori primi di tutti i
fattori sotto radice
= √24 ∙ 7 ∙ 26 ∙ 33 ∙ 3 ∙ 7 = applico le prop. delle potenze
= √210 ∙ 72 ∙ 34 = estrazione di radice
Divido per due tutti gli esponenti
= 25 ∙ 7 ∙ 32 = 32 ∙ 7 ∙ 9 = 2016 𝑐𝑚2












