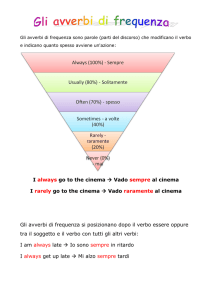
Esempio di test di ingresso per i Corsi di Laurea della classe L-31
“Scienze e tecnologie informatiche”
Il tempo a disposizione per la risoluzione dei quesiti è di 90 minuti.
Il test si ritiene superato se vengono fornite almeno 14 risposte esatte.
1. Si indichi quale delle seguenti frazioni è uguale a
3/2
4/5
(a) 12/5
(b) 15/8
(c) 2/5
(d) 6/5
2. Si dica quale delle seguenti affermazioni è falsa
(a) 3−1 · 32 = 3
(b) 33 /32 = 3
(c) 32 + 33 = 35
(d) (32 )3 = 36
3. Si mettano in ordine decrescente i seguenti numeri reali:
√ √
(a) 3; 2; 5/6; 0,1
√ √
(b) 0,1; 5/6; 2; 3
√ √
(c) 5/6; 0,1; 2; 3
√ √
(d) 0,1; 5/6; 3; 2
√
√
3; 5/6; 2; 0,1
4. Indicare quale delle seguenti affermazioni è vera:
(a) Il prodotto di un numero intero x e del suo successivo è pari oppure dispari a seconda
che x sia pari oppure dispari
(b) Il prodotto di due numeri primi è sempre dispari
(c) La somma di un numero intero x e del suo successivo è sempre dispari
(d) Le precedenti affermazioni sono false
5. Siano x, y , z tre numeri reali diversi da zero. L’espressione
(a) x12 y 2 z 2
(b) x2 y 4 z 2
(c) x6 y 2 z 6
(d) x2 y 4 z 3
(x8 y 2 )2 z 6
è equivalente a
(x2 yz 2 )2
a2
6. Se a e b sono numeri reali diversi da 0, una delle seguenti espressioni non è uguale a
.
b
Quale?
(−a)2
b
a2
(b)
−(−b)
(a)
a2
b
−(−a)2
(d)
−b
(c) −
7. Siano a e b due numeri diversi da zero. L’espressione
√
(a) a 3 b
√
(b) a b
√
(c) b 3 a
√
3 3
a b è equivalente a
(d) b
8. Siano x, y due numeri reali diversi da zero. Si dica quale delle seguenti affermazioni è
vera:
(a) (x − y)(x + y) = x2 + y 2
(b) (x − y)(x + y) = x2 − y 2
(c) (x − y)(x + y) = x2
(d) (x − y)(x − y) = y 2
9. Quale dei seguenti polinomi ha come radice x = 2?
(a) x2 − 5x + 6
(b) x2 + 2
(c) x2 − 2x + 1
(d) x2 − 3x
10. Dati i polinomi P (x) = 3x + 1 e Q(x) = 3x2 + 7x, il polinomio somma P (x) + Q(x) è
(a) 3x2 + 10x
(b) 3x2 + 10x + 1
(c) x2 − 4x
(d) 3x2 + 7x − 1
11. L’equazione x4 + x2 + 1 = 0
(a) ammette quattro radici reali
(b) non ammette radici reali
(c) ammette almeno una radice reale
(d) ammette almeno due radici reali
12. La disequazione
3(2x + 1) − 2
< 0 è verificata
x2 + 1
(a) solo per x < −1/6
(b) solo per −1/6 < x < 1
(c) solo per x < −1
(d) solo per −1 < x < 1
13. La frase “Chi guida veloce non è prudente” è equivalente a:
(a) Chi guida piano è prudente
(b) Chi non è prudente guida veloce
(c) Chi è prudente guida piano
(d) È prudente solo chi guida piano
14. La negazione della proposizione “Ogni mese qualcuno legge almeno un libro” è
(a) Ogni mese qualcuno non legge alcun libro
(b) Ogni mese nessuno legge nemmeno un libro
(c) Ci sono mesi in cui nessuno legge un libro
(d) Ci sono mesi in cui qualcuno non legge nemmeno un libro
15. Nel regolamento ospedaliero c’è scritto: “C’è sempre almeno un medico di guardia al
Pronto Soccorso”. A quale delle seguenti affermazioni equivale?
(a) Non c’è nessun medico che sia sempre di guardia al Pronto Soccorso
(b) Non c’è nessun momento in cui non ci sia almeno un medico di guardia al Pronto
Soccorso
(c) Non ci sono mai due medici di guardia al Pronto Soccorso
(d) C’è un certo medico che è sempre di guardia al Pronto Soccorso
16. Quali delle seguenti proposizioni è la negazione di “Ogni lunedı̀ studio e vado al cinema”?
(a) Ogni lunedı̀ non studio né vado al cinema
(b) In alcuni lunedı̀ né studio né vado al cinema
(c) In alcuni lunedı̀ non studio oppure non vado al cinema
(d) Ogni lunedı̀ studio oppure vado al cinema
17. Tutti gli alunni di una classe giocano a basket o a tennis o a entrambi. Se 15 praticano
entrambi gli sport, 23 il basket e 27 il tennis, quanti sono gli alunni di quella classe?
(a) 27
(b) 35
(c) 38
(d) 65
18. Se 4 operai di una camiceria riescono a confezionare 40 camicie in 20 minuti, quanti operai
occorrerebbero per riuscire a confezionare 400 camicie in 100 minuti?
(a) 40
(b) 4
(c) 8
(d) 20
19. Alla data odierna l’età di nonno Luigi supera di 12 anni il doppio della somma della età
dei due nipotini Stefano e Francesca. Indicate con L, S ed F , rispettivamente, le età
(in anni) di nonno Luigi, di Stefano e di Francesca, scegliere la uguaglianza che descrive
algebricamente la situazione:
(a) L + 12 = 2(S + F )
(b) L = 2(S + F ) + 12
(c) L = 24 + S + F
(d) L = 2(12 + S + F )
20. Scegliere il numero successivo nella sequenza 22 20 17 13 8 . . .
(a) 2
(b) 3
(c) 4
(d) 5
21. L’equazione x2 + (y − 2)2 = 4 rappresenta
(a) una retta
(b) una circonferenza
(c) una ellisse
(d) una parabola
22. L’equazione della retta passante per i punti (0, 0) e (1, 2) è
(a) y = 2x
(b) y = x
(c) y = 3x
(d) y = −x
23. In un triangolo rettangolo, un cateto misura i 4/3 dell’altro. Sapendo che l’area del
triangolo misura 24 cm 2 , la lunghezza del cateto minore è
(a) 6 cm
(b) 18 cm
(c) 8 cm
(d) 16 cm
24. Il rapporto tra l’area del triangolo equilatero di lato ` e quella del cerchio di raggio `
√
(a) è uguale a π 3/4
√
(b) è uguale a `2 3/π
√
(c) è uguale a 3/ (4π)
(d) non si può calcolare perché dipende da `
Risposte esatte
1. (b)
2. (c)
3. (a)
4. (c)
5. (a)
6. (c)
7. (a)
8. (b)
9. (a)
10. (b)
11. (b)
12. (a)
13. (d)
14. (c)
15. (b)
16. (c)
17. (b)
18. (c)
19. (b)
20. (a)
21. (b)
22. (a)
23. (a)
24. (c)