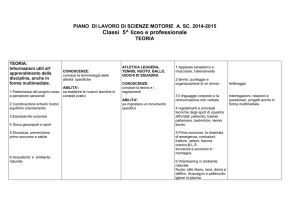
Alcune informazioni sul test di valutazione delle conoscenze di base
Scopo del test è la verifica delle abilità logiche e di ragionamento e delle abilità matematiche, relative
ad argomenti trattati nella scuola media superiore.
Il test consiste di 20 quesiti a risposta multipla; il tempo a disposizione per la risoluzione dei quesiti
è di 60 minuti.
A titolo puramente indicativo, si forniscono alcuni esempi, suddivisi per argomenti.
Abilità logiche e di ragionamento
La frase ”Chi guida veloce non è prudente” è equivalente a:
(a) Chi guida piano è prudente
(b) Chi è prudente guida piano
(c) Chi non è prudente guida veloce
(d) È prudente solo chi guida piano
La negazione della proposizione “Ogni mese qualcuno legge almeno un libro” è
(a) Ogni mese qualcuno non legge alcun libro
(b) Ogni mese nessuno legge nemmeno un libro
(c) Ci sono mesi in cui nessuno legge un libro
(d) Ci sono mesi in cui qualcuno non legge nemmeno un libro
Tutti gli alunni di una classe giocano a basket o a tennis o a entrambi. Se 15 praticano entrambi gli
sport, 23 il basket e 27 il tennis, quanti sono gli alunni di quella classe?
(a) 27
(b) 35
(c) 38
(d) 65
Geometria e geometria analitica
Il rapporto tra l’area del triangolo equilatero di lato ` e quella del cerchio di raggio `
√
(a) è uguale a π 3/4
√
(b) è uguale a `2 3/π
√
(c) è uguale a 3/ (4π)
(d) non si può calcolare perché dipende da `
Il centro della circonferenza di equazione x2 + y 2 − 4x + 2y + 2 = 0 appartiene alla retta di equazione
x + (h − 2)y − h + 2 = 0 per
(a) h = −1
(b) h = 3
(c) h = 0
(d) h = 2
Proprietà dei numeri e manipolazioni algebriche
Se x è un numero reale strettamente negativo, allora
(a) x è maggiore del suo doppio
(b) x è maggiore della sua metà
(a) x è maggiore del suo quadrato
(a) x è maggiore della sua radice quadrata
Il triplo del quadrato del reciproco di (−1/3)−1 è
(a) 1/3
(b) −1/3
(c) −3
(d) 3
Tra i
(a)
(b)
(c)
(d)
numeri 0.56, 3/8, −3/17, 5/8, 0.25, il minore ed il maggiore sono
0.56 e 5/8
0.56 e 0.25
−3/17 e 5/8
−3/17 e 3/8
L’espressione 2x+y 2x−y è uguale a
(a) 2x (2y · 2−y )
2
2
(b) 2x −y
2
2
(c) 2x − 2y
¡ 2 ¢x
(d) 2
Polinomi ed equazioni/disequazioni algebriche
Il polinomio x4 + (h + 1)x3 + 1 ha radice x = −1 per
(a)
(b)
(c)
(d)
h = −1
h=1
h = −3
nessun valore di h
L’equazione 4x4 + 2x2 + 1 = 0
(a) ha almeno una soluzione reale
(b) ha quattro soluzioni reali
(c) ha due soluzioni reali
(d) non ha alcuna soluzione reale
3(2x + 1) − 2
< 0 è verificata
x2 + 1
x < −1/6
−1/6 < x < 1
x < −1
−1 < x < 1
La disequazione
(a)
(b)
(c)
(d)
solo
solo
solo
solo
per
per
per
per