Quantità di Moto
-F
r
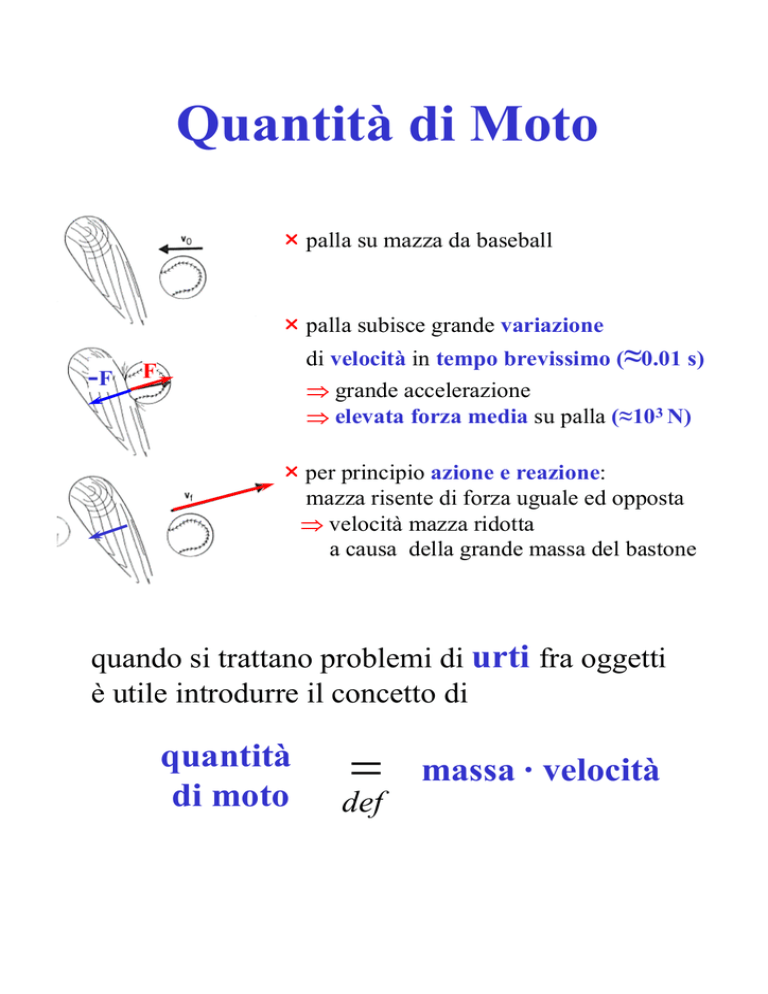
palla su mazza da baseball
r
palla subisce grande variazione
di velocità in tempo brevissimo (≈0.01 s)
⇒ grande accelerazione
⇒ elevata forza media su palla (≈103 N)
F
r
per principio azione e reazione:
mazza risente di forza uguale ed opposta
⇒ velocità mazza ridotta
a causa della grande massa del bastone
quando si trattano problemi di urti fra oggetti
è utile introdurre il concetto di
quantità
di moto
=
def
massa · velocità
r
r
r
p = mv
definizione
non relativistica
(v << c)
p x = mv x
p y = mv y
p z = mv z
r
grandezza vettoriale
r
dimensioni e unità di misura
[ L]
m
[ p] = [ M ] ⋅
⇒ kg ⋅
[T ]
s
esempio: variazione della quantità di moto
r
j
r
j
r prima r
vi
vi
r
vf = 0
dopo
r
vf
m = 0.1 kg
vi = 4.0 m / s
r
∆p = ?
m = 0.1 kg
vf = 0m / s
orsetto
v f = 4.0 m / s
palla
orsetto :
r
r
r
r
r r
r
∆p = p f − pi = 0 − ( − mvi j ) = + mvi j = (0.1kg × 4.0m / s ) j = 0.4 kgm / s j
palla :
r
r
r
r
r r
r
r
∆p = p f − pi = mvi j − ( − mvi j ) = +2mvi j = 0.8 kgm / s j = 2 × ∆porsetto
r
Attenzione: p è una grandezza vettoriale !!!
esempio: pista automobili giocattolo
m = 2.0 kg
vi = 0.50 m / s
v f = 0.40 m / s
r
∆p = ?
r
vi
r
vf
r
r
pi = (2.0 kg )(−0.50 m / s ) j
r
r
p f = (2.0 kg )(0.40 m / s )i
r r
r
∆p = p f − pi
r
r
= (2.0 kg )(0.40 m / s )i − (2.0 kg )(−0.50 m / s ) j
r
r
= (0.8 i + 1.0 j ) kg m / s
r
r
p = mv
p permette di distinguere fra
particelle pesanti e leggere
con stessa velocità
esempio:
v = 10 m/s
m palla-bowling >> m palla-tennis
⇒ ppalla-bowling >> ppalla-tennis
esempio:
un camion e una palla da ping-pong si muovono alla
stessa velocità v = 2 m/s.
Da quale dei due è preferibile essere investiti ?
p descrive la differenza
fra i due oggetti in moto !!!
esempio:
se una bambina piccola (18 kg)
vi corresse incontro,
probabilmente la prendereste in braccio:
è piccola non può far danni.
se un giocatore di football (100 kg)
facesse la stessa cosa,
probabilmente vi scansereste velocemente.
se il giocatore vi venisse incontro
camminando tranquillamente e vi urtasse,
non vi preoccupereste molto.
p descrive la differenza fra i due oggetti in moto
mbambina = 18 kg
vbambina = 3 m / s
pbambina = 54 kg m / s
a che velocità dovrebbe andare il giocatore per avere la
stessa quantità di moto?
mgiocatore = 100 kg
p giocatore = pbambina
mgiocatore v giocatore = mbambina vbambina
v giocatore =
mbambina
vbambina = 54 cm / s
mgiocatore
il giocatore dovrebbe andare MOLTO lentamente!
Seconda legge di Newton
sistemi a massa costante
sistemi a massa variabile
r
r
F
=
m
a
∑
r dpr
∑ F = dt
N.B. se m = costante ritrovo II legge di Newton
r
r dpr d (mvr )
r
dv
∑ F = dt = dt = m dt = ma
esempio di sistemi a massa variabile:
4razzo che espelle combustibile
4palla di neve che rotolando si ingrossa
4camion che si riempie d’acqua mentre viaggia con la pioggia
la quantità di moto di un sistema si conserva
se sul sistema non agiscono forze esterne
r
∑F =0
⇒
r
dp
=0
dt
⇒
r
p = costante
[ I Legge di Newton – Principio di Inerzia]
esempi: conservazione quantità di moto
un razzo a motori spenti procede nello spazio
[lontano da sorgenti gravitazionali]
imponenti petroliere possono percorrere
fino a 10 km dopo che i motori sono stati spenti
Sistema di due particelle:
conservazione quantità di moto
r
r
p1 = m1v1
r
F12 r
F21
r
r
p2 = m2 v2
r
r
F12 = − F21
r
sistema isolato
(non ci sono
forze esterne al sistema)
r
sistema di
2 particelle interagenti
[es. forza interna = gravità]
principio di azione e reazione
tra forze interne
r r
r
∑ F =F12 + F21 = 0
r r
d ( p1 + p2 )
=0
dt
⇒
r
r r
ptot = p1 + p2 = costante
r
r
r
r
p1i + p2i = p1 f + p2 f
pix = p fx
piy = p fy
piz = p fz
conservazione della quantità di moto:
r
la quantità di moto totale
di due particelle isolate interagenti si conserva
r
la quantità di moto totale di un sistema isolato è uguale
in ogni istante alla quantità di moto iniziale
esempi: conservazione quantità di moto
2 pattinatori [su ghiaccio]
r
r
pi = p f
0 = m1v f 1 + m2 v f 2
vf1 = −
m2
vf 2
m1
rinculo [su superficie senza attrito]
0 = m1v f 1 + m2 v f 2
vf1 = −
m2 v f 2
rinculo del fucile [dopo lo sparo]
r r
pi = p f
m1
mP = 20g, mF = 5.0kg
vP = 620m / s
0 = mPvP + mF vF
vF = −
=−
mPvP
mF
0.02kg × 620m / s
= −2.5m / s
5.0kg
esempi: conservazione quantità di moto
esplosione di una stella
foto da
telescopio spaziale Hubble
esplosione violenta
di Eta Carinae (1841):
produzione de lobi simmetrici
[con dimensioni pari a
nostro sistema solare!!!]
che emettono materia
in versi opposti
⇒
la quantità di moto della stella
è rimasta immutata dopo l’esplosione
decadimento di un kaone in quiete
K0 →π + +π −
K0
r
p−
r
p+
π-
π+
r
r
p f = pi = 0
r
r
r
p f = p+ + p− = 0
r
r
p+ = − p−
propulsione nel vuoto:
come fa un razzo o un astronauta a spostarsi nel vuoto ?
[cioè in assenza di attrito]
⇒ con la conservazione di p !!!!
M = massa sistema (M+M)
V = velocità sistema (V+V)
M = massa astronauta
V = velocità dell'astronauta
M = massa carburante
V = velocità dei gas espulsi
conservazione
quantità di moto
astronauta fermo
V=0
astronauta si muove
a velocità V
gas espulso
a velocità V
motori spenti
accendo i motori
MV=0
(V=0 e V=0)
seppie, polipi e meduse
usano lo stesso
sistema di propulsione !!
MV+MV=0
V≠0
⇒V≠0
propulsione di un razzo
[sistema a massa variabile]
durante il moto si conserva la massa del sistema
[massa combustibile + massa navetta]
pi = p f
pi = ( M + ∆m)v
razzo espelle ∆m in ∆t
⇒ velocità aumenta di ∆v
p f = M (v + ∆v) + ∆m(v − ve )
ve = velocità combustibile
rispetto al razzo
v-ve= velocità combustibile rispetto
a sistema di riferimento fisso
( M + ∆m)v = M (v + ∆v) + ∆m(v − ve )
M∆v = ∆m ve
se ∆t → 0
Mdv = −ve dM
vf
Mf
vi
Mi
∫ dv = −ve
∫
dM
M
∆v → dv e ∆m → dm = −dM
v f − vi = −ve ln
Mf
Mi
= ve ln
Mi
Mf
per incrementare velocità:
r elevata ve
r massa Mf piccola
esempio: spinta del razzo
spinta del razzo = forza esercitata
def dai gas si scarico
sul razzo
dv
dM
F = Ma = M
= ve
dt
dt
[Mdv = −v dM ]
e
spinta cresce se:
r aumenta
velocità di scarico ve
r aumenta tasso di consumo R = dM/dt
razzo Saturno V:
Mrazzo,i = 3.00 106 kg
R = dM/dt = 1.50 104 kg/s
ve = 2.60 103 m/s
spinta del razzo: F = ve dM/dt
= (2.60 103 m/s)(1.50 104 kg/s)
= 39.0 106 N = 39 MN
accelerazione al momento del lancio:
r r
r
r
=
+
F
F
F
∑
razzo
g = Ma
Frazzo − Fg = Ma
a=
Frazzo − Fg
M
= 3.20 m / s 2
(39.0 ×106 N ) − (3.00 ×106 kg )(9.8 m / s 2 )
=
3.00 ×106 kg
Impulso e Quantità di Moto
r d pr
F=
dt
seconda legge di Newton:
la quantità di moto varia se
sulla particella agisce una forza
r r
d p = F dt
tf
r
r r
r
∆ p = p f − pi = ∫ F dt
ti
r
I =
def
tf
r
r
F
dt
=
∆
p
∫
ti
Teorema dell’ impulso:
l’ impulso di una forza
(integrale della forza nell’intervallo di tempo)
è pari alla variazione della quantità di moto
[ I ] = [ p ] = [ M ][ L / T ]
I
F può variare nel tempo
I = area sotto la curva forza-tempo
tf
I
1 r
F =
F dt
def ∆ t ∫
ti
r
r
I = ∆p = F ∆t
forza media
stesso impulso
impresso da
forza variabile
La forza media permette di calcolare l’impulso
senza descrivere in dettaglio
la variazione della forza in funzione del tempo
esempio:
la forza tra due oggetti che urtano ha spesso
un andamento complicato e difficilmente descrivibile
Il concetto di impulso è utile quando
una delle forze agenti sulla particella agisce
4per breve tempo
4con intensità elevata
Forza
impulsiva
approssimazione impulsiva:
trascuro gli effetti delle altre forze
[piccoli durante la breve durata di azione delle forze intense]
forze impulsive
sono tipiche dei processi di urto
[di durata brevissima]
I
esempio:
palla su mazza da baseball
∆t ≈ 0.01 s
<F> ≈ 103 N
Fg =mg ≈ (100 g) (9.8m/s2) = (0.1 kg ) (9.8m/s2) ≈ 1 N
<F> >> Fg
⇒ trascuro ogni variazione di velocità legata
a forza di gravità
applicazione: air bag
∆p = F ∆t
variazione
quantità di moto
dell’auto
air-bag:
induce variazione quantità di moto
in intervallo di tempo più lungo
⇒ riduce picco di intensità della
⇒
forza
riduce traumi
applicazione: guantoni da pugile
∆p = F ∆t
i guantoni aumentano tempo
durante il quale la forza
è applicata alla testa
⇒ riduce picco di intensità della
forza
⇒ riduco accelerazione del cranio
⇒ riduco traumi
N.B. nel XIX secolo di combatteva a pugni nudi :
maggiori traumi
esempio: forza su auto durante un urto
In un test d’urto, un’auto di massa m=1500 kg urta contro un muro.
velocità iniziale è vi = -15.0 i m/s
velocità finale è vf = 2.60 i m/s.
durata urto ∆t=0.150 s
determinare impulso dovuto all’urto e forza media esercitata sull’auto
r
r
r
r
4
pi = mvi = (1500 kg )(−15.0 m / s ) i = −2.25 10 i kg m / s
r
r
r
r
4
p f = mv f = (1500 kg )(2.6 m / s ) i = 0.39 10 i kg m / s
r
r
r r
r
4
4
I = ∆p = p f − pi = (0.39 10 i kg m / s ) − (−2.25 10 i kg m / s )
r
= 2.64 10 4 i kg m / s
Forza media esercitata sull’auto:
r
r
4
r
∆p 2.64 ⋅10 i kg m / s
5
F=
=
= 1.76 10 i N
0.150 s
∆t
esercizi quantità di moto










