Soluzioni del giornalino n. 19
http://olimpiadi.ing.unipi.it
Soluzione del problema 1 Soluzioni corrette ci sono pervenute da Leone
Cimetta, Mattia Galeotti, Giuseppe Porcelluzzi
Prendendo i 4 guanti blu, Alessandra è sicura di aver preso una coppia ben
formata. Prendendo solo 3 guanti, comunque li scelga, rischia che siano tutti
quanti destri. Quindi il minimo necessario è 4.
Soluzione del problema 2 Soluzioni corrette ci sono pervenute da Leone Cimetta, Angelo De Marco, Mattia Galeotti, Giuseppe Porcelluzzi, Elia
Santi.
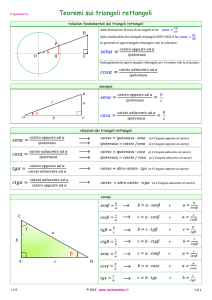
\ =
Sia H il piede dell’altezza da A su BC; per costruzione si ha AHC
◦
\
AHB = 90 e dunque H è la seconda intersezione delle due circonferenze
date e giace su BC.
Si noti che l’ipotesi che il triangolo sia rettangolo è completamente inutile.
Soluzione del problema 3 Soluzioni corrette ci sono pervenute da Leone
Cimetta, Mattia Galeotti, Denis Nardin, Giuseppe Porcelluzzi.
Applichiamo la formula detta in-and-out rule per i coefficienti binomiali:
n
n n−1
=
,
k
k k−1
che è semplice dimostrare sostituendo ai coefficienti binomiali la loro definizione.
Usando tale formula con n = 2m + 1, k = m + 1 si ha
2m + 1
2m + 1 2m
=
.
m+1
m+1 m
Poiché il lato di sinistra è intero, m + 1 deve dividere (2m + 1) 2m
m . Ma
m + 1 e 2m + 1 sono
primi tra loro (perché il resto della loro divisione è −1),
quindi m + 1 | 2m
m , come era da dimostrare.
Soluzione del problema 4 Soluzioni corrette ci sono pervenute da Leone
Cimetta, Mattia Galeotti, Giuseppe Porcelluzzi.
L’equazione di partenza può essere scritta come
(x + y)2 − (xy)2 = (x + y + xy)(x + y − xy) = 1.
1
Gli unici divisori di 1 sono però 1 e −1. Quindi, siccome i fattori trovati
sopra sono anch’essi interi,devono essere entrambi 1 o entrambi −1. Tuttavia,essendo x, y interi positivi,si ha x + y + xy ≥ 3; dunque,non esiste alcuna
coppia di interi positivi (x, y) con queste caratteristiche.
Soluzione del problema 5 Non ci sono pervenute soluzioni.
Suddividiamo il cubo in 27 cubetti di lato 1/3 tagliandolo con piani paralleli
alle facce (come in un cubo di Rubik). Per il principio dei cassetti, esiste
(almeno) uno di questi cubetti contiene (almeno) tre dei punti assegnati,
nell’interno o sul suo bordo. Intendiamo dimostrare che il triangolo formato
da questi tre punti ha area minore di 7/72. Quindi riduciamoci a considerare
solo questi punti e il cubetto di lato 1/3 che li contiene.
Notiamo che, fissati due dei punti, se spostiamo il terzo in un punto che
sia più lontano dal lato formato dai due punti fissati, l’area del triangolo
racchiuso aumenta (perché la base resta costante e l’altezza aumenta). Si
può verificare che, qualunque sia il lato fissato, il massimo della distanza
dal lato si raggiunge mettendo il terzo punto in uno dei vertici del cubetto
(segue, se vogliamo, dalla convessità della funzione distanza).
Se ripetiamo questo procedimento sugli altri due punti, possiamo fare in
modo che tutti e tre i punti vengano spostati sui vertici del cubetto. Quindi
abbiamo dimostrato che, per ogni triangolo contenuto interamente nel cubetto, ne esiste uno che ha i suoi vertici sui vertici del cubetto e ha area
maggiore. Ci basta allora verificare che tutti i triangoli che hanno i loro
vertici sui vertici del cubo hanno area minore di 7/72 otteniamo la tesi.
Tali triangoli possono essere solo di tre tipi, a meno di rotazioni e riflessioni,
e si può calcolarne esplicitamente l’area e verificare che in tutti e tre i casi
7
essa è minore di 72
.
Soluzione del problema 6 Non ci sono pervenute soluzioni.
Supponiamo che le caselle della scacchiera abbiano lato unitario, e sia S
la figura formata dall’unione di tutte le case ammalate ad un dato tempo;
vogliamo dimostrare che il perimetro dell’insieme S non può mai aumentare
lungo il tempo.
Controlliamo cosa succede intorno a una nuova casa che si ammala: almeno
due case confinanti sono già ammalate, e queste case possono essere disposte lungo due lati opposti o adiacenti. Esaminando entrambi questi casi,
possiamo notare che vengono eliminati dal contorno di S due segmenti di
lunghezza unitaria e ne vengono aggiunti due nuovi, quindi il suo perimetro resta invariato. Se invece una casa sana si ammala perché confina con
tre o quattro case ammalate, si verifica nello stesso modo che il perimetro
dell’insieme diminuisce strettamente.
Se le case ammalate inizialmente sono 7, il loro perimetro misura al più
7 · 4 = 28. Se per assurdo fosse possibile arrivare alla situazione finale in cui
tutte le case sono ammalate, il perimetro di S misurerebbe invece 32. Ma
2
abbiamo appena dimostrato che tale perimetro non può aumentare, quindi
è impossibile raggiungere tale configurazione finale.
Soluzione del problema 7 Una soluzione corretta ci è pervenuta da Mattia
Galeotti.
Una soluzione sostanzialmente corretta ci è pervenuta da Leone Cimetta.
Notiamo subito che HP JB è ciclico in quanto ha due angoli opposti retti
\=P
\
e dunque si ha HJP
BH = 60◦ − P[
BJ; similmente, poichè KP JC è
\
\
ciclico (per lo stesso motivo), si ha P
JK = P
CK = 60◦ − P[
CJ.
◦
◦
\
[
[
\
Sommando, HJK = 120 − P BJ − P CJ = BP C − 60 . Dunque la condi\ = 90◦ è verificata se e solo se lo è la condizione BP
\
zione HJK
C = 150◦ ;
quindi il luogo richiesto è l’arco di circonferenza, interno ad ABC che vede
BC sotto un angolo di 150◦ .
Soluzione del problema 8 Non ci sono pervenute soluzioni corrette.
Sia p(n) il numero delle permutazioni di 1, 2, . . . , n tali che l’1 resta fisso e
ogni numero differisca dai suoi vicini al più di 2.
Il primo numero deve essere l’1, quindi il secondo deve essere 2 o 3. Se il
secondo numero è 2 allora il numero di permutazioni di 2, 3, . . . , n in cui il 2
è fissato e ogni numero differisce dai suoi vicini di al più 2 è p(n − 1). Se il
secondo numero è 3, allora il terzo numero è 2, 4 o 5. Se è 2, allora il quarto
deve essere 4. In questo caso il numero di permutazioni di 4, 5, . . . , n in cui
il 4 è fissato e ogni numero differisce dai suoi vicini di al più 2 è p(n − 3).
Supponiamo allora che il terzo numero non sia 2.
Allora il 2 non sta vicino né all’1 né al 3; poiche gli unici numeri che
differiscono di al più 2 dal 2 sono 1,3,4, il 2 dovrà essere collocato in
ultima posizione, preceduto dal 4. Quindi il 3 sarà seguito dal 5, e il
4 sarà preceduto dal 6 ecc. Si ottiene quindi la seguente permutazione:
1, 3, 5, 7, . . . , 2003, 2005, 2004, 2002, . . . , 6, 4, 2. Quindi si ha p(n) = p(n −
1) + p(n − 3) + 1. Inoltre si ha p(1) = 1, p(2) = 1, p(3) = 2.
Quindi si calcolano i successivi valori di p(n) modulo 3 (in quanto è richiesto
solo il valore di p(2005) modulo 3), finché non si trova un periodo (cioè finché
non si trova k tale che p(k) = p(1) mod 3, e p(k + 2) = p(3) mod 3). Si
hanno (modulo 3) i seguenti valori:
1
1
2
1
3
2
4
1
5
0
6
0
7
2
8
0
9
1
10
1
11
2
12
1
Come si vede dalla tabella si trova k = 9. Quindi il periodo dei valori di
p(n) modulo 3 ha lunghezza 9 − 1 = 8. Dato che 2005 = 5 mod 8, si ha
p(2005) = p(5) = 0 mod 3. Quindi 3 divide p(2005).
Soluzione del problema 9 Non ci sono pervenute soluzioni.
3
Siano d1 e d2 le diagonali di Q. Consideriamo la famiglia delle rette perpendicolari a d1 che intersecano Q; ciascuna di queste rette deve incontrare
(almeno) un li e quindi l’unione delle proiezioni dei segmenti sulla diagonale
la ricopre completamente. Indicata
con π√
1 (li ) la lunghezza della proiezione
P
di
l
su
d
,
abbiamo
allora
π
(l
)
≥
2. Nello stesso modo si ottiene
1 √
i 1 i
P i
2.
i π2 (li ) ≥
Di conseguenza
√
√
X
X
2X
2 √ √
2
2 1/2
li =
(π1 (li ) +π2 (li ) ) ≥
(π1 (li )+π2 (li )) =
( 2+ 2) = 2.
2
2
i
i
i
Soluzione del problema 10 Non ci è pervenuta alcuna soluzione.
Suddividiamo ogni esagono in 6 triangoli equilateri congruenti. Cosı̀ facendo
si ottiene una tassellatura del piano in triangoli equilateri tutti a due a due
congruenti. Dimostreremo più in generale che non è possibile costruire un
quadrato che abbia tutti i vertici coincidenti con i vertici dei triangoli (In
pratica abbiamo ammesso l’ulteriore possibilità che il quadrato abbia un
vertice nel centro di un esagono). Supponiamo inoltre che i triangoli abbiano
lato unitario.
Procediamo per assurdo: supponiamo esista un quadrato ABCD che abbia
come vertici i vertici dei triangoli. Sia s la lunghezza di AB.
Lemma 1. Esiste un triangolo AXB esterno al quadrato ABCD, dove AX
e XB sono unioni di lati di triangoli della tasselatura.
Dimostrazione. Prendiamo due coppie di rette parallele, non coincidenti,
della tasselatura, due passanti per A, due passanti per B; queste linee
determinano un parallelogramma AQBX, dove X si prende esterno ad
ABCD.
Esistono analogamente i triangoli BY C, CZD e DW A ognuno esterno ad
ABCD.
Lemma 2. Il quadrato ABCD ha area intera.
Dimostrazione. Siano k la lunghezza di AX, e m la lunghezza di XB; k ed
m sono interi per il lemma precedente. Dal momento che AX̂B è un angolo
di 60 o di 120 gradi, si ottiene facilmente che s2 = k 2 + m2 − km oppure
che s2 = k 2 + m2 + km. In ciascuno dei due casi s2 , che è l’area di ABCD,
risulta essere un intero.
√
Si può facilmente calcolare l’area di AXB, che vale km
3
4 . √
L’area della regione R = AXBY CZW A vale quindi s2 + n 43 , dove n è la
somma dei contributi dei quattro triangoli esterni al quadrato, e s2 è l’area
4
del quadrato. Si noti che n è intero in quanto somma di quattro termini del
tipo km, con k e m interi. Tuttavia la regione R contiene al suo interno un
numero
intero N di triangoli della tasselatura, perciò la sua area deve essere
√
N 43 . Eguagliando le due espressioni dell’area di R si ottiene:
√
3
2
s = (N − n)
4
Se fosse N = n si avrebbe s = 0 assurdo, quindi N 6= n.√
Quindi abbiamo che s2 , che è intero, è uguale a (N − n) 43 , che è irrazionale.
Assurdo.
Soluzione del problema 11 Non ci sono pervenute soluzioni corrette.
Disegniamo sul piano una griglia di lato 1/2 in modo che il vertice in basso
a sinistra di R sia sulla griglia e che i lati di R siano paralleli alle rette
della griglia, e coloriamone le caselle alternativamente di bianco e nero come
in una scacchiera. È facile vedere che se un rettangolo con i lati paralleli
alle rette della griglia è disprezzabile, allora la porzione della sua superficie
colorata di bianco è uguale a quella colorata di nero (e diciamo che è equicolorato). Infatti supponiamo per esempio che sia la base ad avere lunghezza
intera: se il lato sinistro e quello destro del rettangolo sono sulla griglia (il
rettangolo è “centrato”) l’asserzione è evidente (il rettangolo si suddivide in
colonne di base 1 ciascuna delle quali è equicolorata); se invece il rettangolo
è sfasato rispetto alla griglia, si può trasformarlo in un rettangolo disprezzabile centrato aggiungendo e togliendo ai lati due colonnine uguali. Abbiamo
dunque dimostrato che disprezzabile ⇒ equicolorato.
Ora anche R, che è piastrellato con rettangoli equicolorati, sarà equicolorato:
vogliamo mostrare che è disprezzabile. Supponiamo per assurdo che né la
sua base né la sua altezza siano numeri interi. A meno di sottrarre da R dei
rettangoli disprezzabili (cosa che non ne cambia la disprezzabilità), possiamo
supporre che la sua base e la sua altezza siano dei numeri x e y strettamente
compresi fra 0 e 1. Semplici calcoli mostrano che ciò è in contraddizione
con l’ipotesi che R sia equicolorato: supponiamo per esempio che il primo
rettangolino 1/2 × 1/2 in basso a sinistra sia bianco, e analizziamo i quattro
casi:
• x ≤ 1/2, y ≤ 1/2: allora R è tutto bianco;
• x ≤ 1/2, y > 1/2: la parte bianca ha area x/2, la parte nera ha area
x
y− 21
2
, che è minore di x/2;
• x > 1/2, y ≤ 1/2: analogo a sopra;
• x > 1/2, y > 1/2: la parte bianca ha area 41 + (x − 12 )(y − 12 ), la parte
nera ha area 12 (x − 12 ) + 12 (y − 12 ): provare che la prima è maggiore
della seconda si riduce a verificare che (x − 1)(y − 1) > 0.
5
Soluzione del problema 12 Una soluzione corretta (mancante della Bonus
Question) ci è pervenuta da Sisifo.
Risolviamo direttamente il quesito nel caso più generale della Bonus Question.
Utilizziamo la notazione vettoriale e poniamo l’origine in D; chiamiamo
~a, ~b, ~c i vettori che individuano i punti A, B, C. Allora possiamo scrivere il
punto D0 come p~a + q~b + r~c con p + q + r = 1 e p, q, r > 0.
Quindi, un punto della parallela a DD0 per A è della forma ~a +s(p~a +q~b+r~c);
q
r
se poi imponiamo s = −1/p, il punto − ~b − ~c sta nel piano DBC e dunque
p
p
è A0 .
r
p
q
p
Similmente B0 è dato da − ~a − ~c e C0 è − ~a − ~b.
q
q
r
r
Ricordiamo che un tetraedro che ha come vertici i punti individuati dai
vettori ~x, ~y , ~z e l’origine, ha volume V = 16 |(~x ∧ ~y ) · ~z|: dunque, il volume di
ABCD è V = 16 |(~a ∧ ~b) · ~c| e il volume di A0 B0 C0 D0 è
1 q ~
r
p
r
~
V0 = p~a + q +
b+ r+
~c ∧
p+
~a + q b + r +
~c ·
6
p
p
q
q
p
q ~
· p+
~a + q +
b + r~c r
r
Ora basta sviluppare l’espressione qui sopra ricordando le seguenti proprietà
del prodotto vettoriale, che valgono per tutti i vettori ~u, ~v , w:
~
1. ~u ∧ ~u = 0
2. (~u ∧ ~v ) · w
~ = (~v ∧ w)
~ · ~u = (w
~ ∧ ~u) · ~v
3. (~u ∧ ~v ) · ~u = (~u ∧ ~v ) · ~v = 0
Si ottiene dopo un po’ di lavoro V0 = (2 + p + q + r) (~a ∧ ~b) · ~c e dunque il
rapporto tra i volumi è V /V0 = 3 per ogni punti D0 all’interno del triangolo
ABC.
6