Nicola GigliettoA.A. 2013/14
Parte I
Cap 4.1- Lavoro ed energia
Cap 4.1- Lavoro ed energia
Abbiamo visto come applicare le leggi della dinamica in varie situazioni.
Spesso però l’analisi del moto spesso risulta complicata o in altri casi si
verifica che la forza agente è variabile nel tempo (e quindi anche l’accelerazione). Esiste un approccio alternivo all’analisi del moto che si realizza
introducendo i concetti di lavoro ed energia.
4.1 - Lavoro di una forza costante
4.1 - Lavoro di una forza costante
4.1 - Lavoro di una forza costante
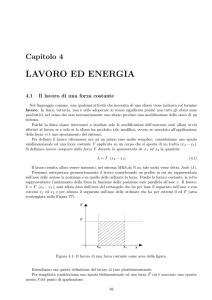
Il lavoro svolto da una forza F è definito dal seguente prodotto scala~ · ∆s
~ = F∆scosθ = (Fcosθ)∆s = Fs ∆s ovvero il lavore: L = (W) = F
ro è pari al prodotto della componente della forza nella direzione dello
spostamento, moltiplicato per lo spostamento stesso.
Dalla definizione se una forza è perpendicolare allo spostamento il lavoF
θ
Fs
s
ro risulta nullo.
Tale definizione comporta che il
lavoro ha un segno: se l’angolo θ tra la forza e lo spostamento è θ ≤ 90◦ il
lavoro è positivo altrimenti sarà negativo; in quest’ultimo caso la componente della forza nella direzione dello spostamento è di conseguenza opposto
allo spostamento stesso. Unità di misura: per il lavoro si usa il Joule e 1
Joule = 1 Newton · 1m ed è la stessa unità di misura dell’energia.
Parte II
4.4 Lavoro compiuto da forze variabili
Lavoro ed energia
1
Nicola GigliettoA.A. 2013/14
4.4 Lavoro compiuto da forze variabili
Lavoro compiuto da forze variabili
Lavoro compiuto da forze variabili (lungo il percorso)
Estendiamo la definizione
R xf usando gli integrali Se lo spostamento è diretto lungo x si ha: L = xi Fx dx è il lavoro compiuto in uno spostamento
sull’asse x.
In generale per una forza ed uno spostamento
R B con qualunque direzione si
~ per cui scomponen~ · ds
ottiene che se la forza è un integrale di linea A F
~ = Fx î + Fy ĵ + Fz k̂ per calcolare il lavoro dobbiamo prima consido si ha F
~ = dx î + dy ĵ + dz k̂ di conseguenza
derare lo spostamento infinitesimo ds
~ = Fx dx + Fy dy + Fz dz. Possiamo ri~ · ds
il lavoro infinitesimo è dL = F
Rr
Rx
Ry
Rz
condurre il caso generico ad una somma di 3 integrali: L = rif dL = xif Fx dx + yif Fy dy + zif Fz dz
(~
ri = xi î + yi ĵ + zi k̂ e r~f = xf î + yf ĵ + zf k̂ sono i vettori posizione iniziale e
finale) Il lavoro è additivo, ovvero il lavoro è pari alla somma dei
lavori delle singole forze agenti. Vediamo alcune applicazioni:
(4.2) Lavoro della forza peso
(4.2) Lavoro della forza peso
Calcoliamo il lavoro per uno spostamento generico:
L=
Z
B
A
~ =
~ · ds
F
Z
−mg
Z
B
A
yB
yA
Z
~ =
(−mg)ĵ · ds
dy = mg(yA − yB )
Il lavoro della forza peso dipende solo dal dislivello (non dipende
dal percorso)
(4.3) Lavoro svolto da una molla
(4.3) Lavoro svolto da una molla
Le molle seguono la legge di Hooke F=-kx che descrive ad esempio il caso di
una molla che si può muovere lungo l’asse x. Il lavoro necessario a spostare
Lavoro ed energia
2
Nicola GigliettoA.A. 2013/14
una molla dalla sua posizione di riposo (che assumiamo essere x=0) è
L=
Z
B
~ =
(Fel )ûx ds
A
Z
xf
(−kx)dx =
xi
1
1
− kx2 |xxfi = − k(x2f − x2i )
2
2
Parte III
4.1 - Teorema del lavoro e dell’energia cinetica
4.1 - Teorema del lavoro e dell’energia cinetica
Definiamo come Energia Cinetica la forma di energia connessa allo stato di moto di un corpo e si definisce come K = (Ek ) = 21 mv2 e si misura
anch’essa in Joule. Il teorema stabilisce che L = ∆Ek = Ek,f − Ek,i ovvero
che il lavoro compiuto da una forza comporta una variazione di energia cinetica. Questa espressione permette di definire anche l’energia (in generale)
come la capacità di un corpo a compiere un lavoro. La definizione
generaleRdel lavoro (per comodità considero
R xf solo uno spostamento lungo x)
xf
è : L = xi Fx (x)dx e Fx = max ⇒ L = xi max dx esplicitiamo la funzione
integranda:
dvx
dvx dx
dx = m
dx =
dt
dx dt
dvx
dx = mvx dvx
= mvx
dx
max dx = m
avendo usato
delle funzioni composte. Quindi si otR x le regole di Rderivazione
v
vx,f
tiene L = xif Fx (x)dx = vx,i
mvx dvx = [ 12 mvx2 ]vx,f
x,i Se teniamo conto anche
delle altre componenti risulterà quindi L = 12 mvf2 − 12 mvi2 = ∆Ek = ∆K
Di conseguenza il teorema si può applicare in qualunque situazione (ad
esempio quando F ed a sono variabili). Pertanto abbiamo dimostrato il teorema, che stabilisce che l’energia cinetica aumenta se il lavoro è positivo o
diminuisce se il lavoro è negativo. In altre parole possiamo anche dire che
l’energia cinetica è pari al lavoro necessario a portare alla velocità
v un corpo inizialmente fermo o il lavoro cambiato di segno per
fermare un corpo di massa m in moto con velocità v.
Lavoro svolto da una generica forza in 3d
Lavoro ed energia
3
Nicola GigliettoA.A. 2013/14
1
ESERCIZIO
Lavoro svolto da una generica forza in 3d
Concludiamo questa parte di teoria verificando la validità del teorema anche
nel caso di forza qualunque con direzione generica: il lavoro infinitesimo
~ = Fx dx + Fy dy + Fz dz per
~ · ds
scritto in termini delle componenti: dL = F
R r~f
R xf
R yf
R zf
~ =
~ · ds
cui il lavoro totale è L = r~i F
xi Fx dx + yi Fy dy + zi Fz dz e
per ognuna delle componenti valgono i teoremi dimostrati prima.
Potenza
Potenza
Definiamo come Potenza la rapidità con la quale viene sviluppato un lavoro nel tempo ovvero in termini matematici: P̄ =< P >= ∆L
∆t (Potenza
istantanea)
La
potenza
si
misura
in Watt
media) P = dL
(Potenza
dt
(W): 1W=1J/1s Dalla stessa definizione è possibile dare una unità di misura alternativa per l’energia: L =< P > ∆t ⇒ Watt x secondi = Joule
(energia) ad esempio: 1 wattora (1 watt · 1 hr) = 1 W · 3600 s= 3600 J
e analogamente per i multipli.
Legame Potenza-Forza
d ~ ~
~
P = dL
dt = dt (F · ds) = F ·
d~
s
dt
~ ·~
=F
v (per F costante)
Verifiche
Quale affermazione delle seguenti è l’unica corretta?
~ e~
[¡+-—alert@+¿]Il lavoro è dato dal prodotto vettoriale di F
s Il lavoro è Fs, con F forza e s spostamento Un lavoro positivo fa aumentare
l’energia cinetica Il lavoro non è mai negativo La 3) è quella giusta
1
Esercizio
Esercizio
Una cassa di M=15 Kg è trascinata in salita su una piano rampa liscia a
velocità costante, per una distanza d= 5.7 m e fino ad una altezza h=2.5 m
rispetto al punto di partenza, ed infine si arresta. Calcolare:
1.
4.
3.
2. il lavoro svolto dalla forza peso;
2. il lavoro della tensione T della fune usata.
Lavoro ed energia
4
Nicola GigliettoA.A. 2013/14
3
PROBLEMA 7.17
Soluzione: 1) la forza peso è costante quindi il lavoro è dato da L =
~ · d~ = mgcos(90◦ +θ)d = −mgsinθd e θ è l’inclinazione della rampa rispetto
P
all’orizzonte data anche da sinθ = hd quindi L = −mgd hd = −15Kg9.8m/s2 ·
2.5m = −368J 2) La tensione della fune T non è nota quindi non possiamo
sapere se è una forza costante a meno che non risolviamo la dinamica del
sistema (quindi fare il bilancio delle forze ecc.) Tuttavia possiamo usare il
teorema del lavoro e dell’energia nella forma generica e applicata a tutte le
forze agenti:
R L = ∆Ek = 0 perchè il corpo parte da fermo e si ferma alla
~ = LP + LN + LT Il primo termine è già noto,
~ +T
~ +N
~ ) · ds
fine. L = (P
N è la reazione normale del piano che essendo normale è perpendicolare
allo spostamento che è parallelo al piano. Quindi LN = 0 ed in definitiva
LP + LT = 0 ⇒ LT = −LP = +368J
2
Problema 7.8
Problema 7.8
Un blocco di massa M=0.4 Kg scivola, con velocità costante v=0.5 m/s, su
un piano orizzontale privo di attrito. Il blocco si arresta comprimendo una
molla collocata sul suo percorso. Se la costante elastica è k=750 N/m di
quanto viene compressa la molla?
Rx
Rx
Il lavoro per comprimere una molla è L = xif F (x)dx = xif (−kx)dx =
− 21 k(x2f − x2i ) e nel nostro caso xi = 0 è la posizione a riposo della molla e
xf è la posizione finale ignota. Applichiamo il teorema L = ∆K = − 12 kx2f
e per l’en. cinetica ∆Ek = 21 (M vf2 − M vi2 ). La velocità finale eec vf = 0
q
M v2
quindi − 21 kx2f = − 12 M vi2 da cui x2f = k i ⇒ xf = M
k vi = 1.2cm.
3
Problema 7.17
Problema 7.17
Un elicottero recupera un uomo di massa M=72 Kg, sollevandolo di 15 m,
con una accelerazione pari a 0.1g. Calcolare il lavoro fatto sull’uomo:
a) dall’elicottero;
b) dalla forza peso;
c) la velocità e l’energia cinetica dell’uomo un attimo prima di entrare
nell’elicottero.
Lavoro ed energia
5
Nicola GigliettoA.A. 2013/14
4
ESERCIZIO
Durante la salita si ha T − Mg = Ma il lavoro fatto
R h dall’elicottero è
il lavoro fatto dalla tensione della fune W = L = 0 T dxricavando T
dall’eq. della dinamica T = M (g + a) = 72(1 + 0.1)g = 79.2 · g N ⇒
4
Lel = T · h = 79.2 · 9.8 · 15 J = 1.2 · 104 J LP = −M gh = −1.1
q · 10 J
Ltot = Lel + LP = ∆Ek = 21 Mvf2 ⇒ Ltot = 0.1 · 104 J e vf =
5.4 m/s
4
2Ltot
M
=
Esercizio
Un blocco di massa M è tirato da fermo da una forza F. Considerando che M=6Kg e F=12N, calcolare la velocità del blocco dopo
aver percorso un tratto di s=3m, sia nel caso del piano liscio che il
caso del piano scabro, con µd = 0.15. Nel caso il piano sia liscio e senza
attrito possiamo utilizzare il teor. lavoro-en.cinetica dal momento che si vuole sapere solo la velocità finale (cambiava totalmente la risoluzione se si vole~ +N
~ +P
~ )·~
va conoscere il tempo impiegato): il lavoro complessivo è L = (F
s
~
~
ma N e P sono ⊥ a ~
s quindi risulterà L = F s = ∆Ek e poichè vi = 0 als
2·12·3 2 2
lora si ha F s = 21 M vf2 da cui ricaviamo vf2 = 2F
M =
6 m /s per cui
√
vf = 12m/s = 3.5m/s Nel secondo caso agisce anche la forza di attrito
che risulta essere costante e pari a Fa = µd N = µd M g ed il lavoro totale è
L = (F − Fa )s = F s − µd N s = F s − µd M gs con il segno meno che nasce dal
fatto che la forza di attrito ha verso opposto allo spostamento. In realtà tutte le forze di attrito producono lavori negativi in quanto oppongono resistenza al moto e tendono a ridurre l’energia cinetica. Facciamo i conti:
Fa = 0.15·6·9.8N = 8.82N quindi L = (F −Fa )s = (12−8.82)·3J = ∆Ek ⇒
a )s
= 3.18m2 /s2 ⇒ vf = 1.8m/s
vf2 = 2(F −F
M
Esercizio 22P
Esercizio 22P
Un blocco di 250 Kg è lasciato cadere su una molla verticale avente
costante elastica k=2.5N/cm. Il blocco rimane poggiato sulla molla
che si comprime di 12 cm prima di fermarsi. Durante la compressione quale lavoro viene svolto (a) dalla molla, (b) dalla forza di gravità
(c) qual’era la velocità del blocco al momento dell’urto con la molla?
(d) raddoppiando la velocità quanto diventa la compressione della molla? k = 2.5 N/cm = 250 N/m a) Lavoro molla: L = − 21 k(x2f − x2i ) =
Lavoro ed energia
6
Nicola GigliettoA.A. 2013/14
4
ESERCIZIO
− 12 kx2 = −125 · (0.12)2 J b) Lavoro gravita’ L = mgh > 0 non sapendo h
possiamo usare il teorema lav-en. cinetica: L = Lp + Lm = 0
Esercizio 7.31 (ed.VI)
Esercizio 7.31 (ed.VI)
La cabina di un montacarichi a pieno carico ha una massa complessiva di
1200 kg e deve salire di 54 m in 3 min. Il contrappeso ha una massa di
950 kg. Supponendo il movimento a velocità costante trovare la potenza
richiesta al motore quando il cavo solleva la cabina. Complessivamente
se la cabina sale (lavoro negativo), il contrappeso scende (lavoro positivo) e
si ha che LM − Mg · 54 + mg · 54 = 0 (non varia l’en. cintetica) per cui il
lavoro del motore è LM = (1200 − 950) · 9, 8 · 54 = 132.3 kJ la potenza è
132300
L
∆t = 180 = 735 W
Esercizio 7.46 (ed VI)
Una cassa di massa 230 kg è sospesa tramite una
fune lunga 12,0 m. Spingendo orizzontalmente sulla cassa con una forza
F variabile, la spostiamo di 4 m sul piano orizzontale.
1. a) Qual’eec l’intensità della forza nella posizione finale?
2. b) Qual’è il lavoro totale fatto sulla cassa?
3. c) Qual’è il lavoro fatto dalla sola peso e dalla fune?
Per i punti b) e c) tenere conto che all’inizio e alla fine la cassa è ferma.
Nella posizione finale abbiamo una situazione di equilibrio il diagramma
delle forze ci suggerisce le seguenti equazioni: x: F − T sin θ = 0 e y:
Mg
d
+T cos θ−Mg = 0 pertanto T = cos
θ e F = T sin θ = Mg tan θ e tan θ = L
4
per cui F = 230 · 9, 8 12 = 751, 3 N b) Il teorema del lavoro-en.cinetica ci
dice che L = LF + LP + LT = ∆Ek = 0 pertanto il lavoro totale è nullo
inoltre LP = M~g · d~ = 0 (perchè . . . ) e LF = F~ · d~ = F · d =
Lavoro ed energia
7