CLASSE : VA E.T.A. 2008-2009
ALUNNO: Bovino Silvano
ANALISI E DESCRIZIONE DI UN OSCILLATORE A PONTE DI WIEN
Si definiscono oscillatori sinusoidali, quei circuiti che restituiscono in uscita un segnale sinusoidale persistente. Un
oscillatore tradizionale è composto in primo luogo da elementi attivi quali i BJT, i FET e gli amplificatori
operazionali(A.O.) che richiedono un alimentazione, mentre in secondo luogo vi è una reazione di tipo positiva che
permette l’autoeccitazione del circuito. Per autoeccitazione si intende la possibilità di riportare in entrata parte della
potenza ottenuta in uscita, in modo tale che il circuito non richieda segnali esterni per poter svolgere la sua funzione.
Un esempio eloquente di come l’autoeccitazione produca un suo effetto è quello dell’altoparlante rivolto
direttamente verso il microfono. Nel momento in cui il segnale captato dal microfono è amplificato e riportato in
uscita dall’altoparlante, cioè l’attuatore, questi è nuovamente riportato in ingresso dal microfono. L’autoeccitazione
provoca in questo caso un segnale fastidioso all’orecchio umano perché simile ad un fischio ma che evidenzia il
fenomeno dell’autoeccitazione. Se il circuito fosse ideale, il guadagno ottenuto sul segnale sarebbe infinito poiché
esso verrebbe amplificato ogni volta che viene riportato in ingresso. Nei circuiti reali ciò non avviene per la presenza
delle perdite caratteristiche di ogni circuito e rete elettrica usati nella pratica.
La teoria degli oscillatori basa le sue radici sui criteri di stabilità dei sistemi retro azionati di Nyquist. Da tali criteri si
ottiene in particolare la relazione fondamentale che, nel momento in cui viene verificata, consente di definire il
relativo circuito, un oscillatore. Questa relazione, derivata dal criterio di Barkhausen, si ottiene nel momento in cui è
presente un segnale di frequenza f0 tale da permettere che la funzione guadagno di anello rispetti la seguente
equazione:
=1
Tale relazione si ottiene immaginando di isolare tra loro i 2 blocchi che costituiscono il sistema(il nostro circuito) nel
punto A, che si trova all’uscita della maglia di reazione. Si osservi a proposito la figura seguente:
Fig.1 Schema a blocchi di un oscillatore
Esaminando il sistema si ottiene la seguente relazione di uscita:
=
∙
∙
Chiamato Vr il segnale in uscita al blocco H si ottiene che:
=
∙
I rapporti al secondo membro rappresentano rispettivamente i blocchi G(jω) e H(jω) del sistema. Si ottiene che il
rapporto Vo/VA definisce la funzione guadagno di anello GH.
Affinché sia rispettata la condizione di Barkhaussen si ottiene che:
=1
=
Se viene rispettata tale condizione, il circuito sarà in grado di generare un segnale sinusoidale di ampiezza costante.
In caso diverso se GH<1 il segnale di uscita tenderebbe a diminuire fino a raggiungere uno stato di stabilità del
sistema. Nel caso GH>1, il segnale di uscita tenderebbe ad aumentare all’infinito ma in realtà l’ampiezza non
raggiungerà mai il livello della tensione di alimentazione del circuito.
Un altro aspetto fondamentale riguarda il fatto che il circuito non richiede un segnale di ingresso o di avvio per
l’eccitazione, in quanto a questo scopo intervengono i segnali di offset o di rumore e i segnali spuri che si generano
inevitabilmente all’accensione del circuito. Quasi sicuramente lo spettro di tali segnali contiene la frequenza f0
necessaria affinché la funzione guadagno di anello sia pari ad 1 e lo sfasamento sia 0. Tale frequenza si definisce:
=
2
Durante la progettazione è dunque indispensabile provvedere alla verifica del criterio di Barkhausen facendo in
modo che la funzione guadagno di anello sia almeno GH>1. In tal modo sarà possibile in seguito riottenere
l’equazione fondamentale degli oscillatori implementando dei circuiti di tipo CAG per il controllo automatico del
guadagno.
Uno degli oscillatori maggiormente conosciuti è l’Oscillatore a ponte di Wien. Questi fu elaborato nel 1891 da Max
Vien a livello teorico. La sua idea fu portata a termine da William Hewlett che perfezionò l’idea originale potendo
utilizzare gli elementi attivi di cui Vien non disponeva all’epoca della sua idea. Il progetto di Hewlett fu mostrato
all’università di Stanford ed è divenuto anche uno dei componenti fondamentali dei primi oscillatori della famosa
ditta di Computer HP.
Il circuito di Hewlett era caratterizzato da una reazione positiva che prelevava su una reazione negativa. La reazione
positiva consentiva l’autoeccitazione del circuito attraverso il criterio di Barkhausen, mente la reazione negativa
consentiva di introdurre un attenuazione nel guadagno in modo tale da evitare le condizioni di saturazione che
provocano l’appiattimento dei vertici delle onde sinusoidali. L’idea di Hewlett per ovviare comprendeva l’utilizzo di
elementi elettrici in grado di attenuare il guadagno. Il circuito quindi è congegnato in modo che un aumento della
resistenza prodotto da un aumento del livello del segnale, comporti una riduzione del guadagno.
Attualmente a questo scopo sono utilizzati transistor FET o fotocellule, ottenendo distorsioni inferiori allo 0,0008%
(8 parti per milione) con piccole variazioni rispetto al circuito originale.
Nell’esercitazione che segue si esaminerà un circuito oscillatore simile e si verificheranno sperimentalmente e
teoricamente i valori della frequenza di oscillazione e della condizione di oscillazione.
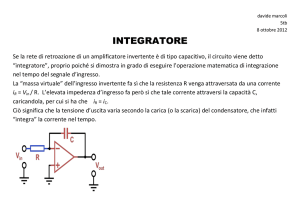
Schema elettrico:
Descrizione e svolgimento pratico:
Il circuito in figura rappresenta un oscillatore a ponte di wien. Tale circuito è definibile oscillatore poiché non vi è
applicato alcun segnale di ingresso ed inoltre vi è una reazione positiva che prevale su quella negativa.
L’amplificatore operazionale è a doppia alimentazione e svolge la funzione di amplificatore non invertente. La sua
funzione di uscita sarà dunque:
=
[1 +
2
]
1
Non essendovi segnale di ingresso applicati, è chiaro che la tensione applicata all’ingresso non invertente
dell’operazionale sia la Vp. La Vp è ottenuta dal partitore di tensione formato dai rami C-R e quindi dalle 2
impedenze. Se isoliamo i blocchi A e B del circuito come spiegato inizialmente si ottiene che:
=
∙
2
1+ 2
Dove Z1 è composto dalla serie C-R mentre Z2 è composto dal parallelo C-R.
Risolvendo il circuito si ottengono le seguenti relazioni che definiscono rispettivamente l’ampiezza del segnale di
uscita, la frequenza di oscillazione e la condizione di oscillazione:
=
+2
=
2
1
1+ 2
2
2≥2 1
Il nostro obbiettivo è quello di confrontare i valori ottenuti dai calcoli teorici, con quelli verificati sperimentalmente
attraverso l’analisi della curva di risposta del circuito.
R1
R2
R
Rx
C
Vd
Vz
TABELLA DATI
Ry+Rx
47k
47k
18k
1nF
0.6V
6.7V
Come si osserva dalla tabella, il valore della R1, essenziale per stabilire la condizione di oscillazione, è definito dalla
somma del valore di Rx e del valore di resistenza del potenziometro. Affinché sia rispettata la condizione di
oscillazione dunque, è necessario che 2R1=47k. Si ottiene che affinché tale relazione sia rispettata, il valore di Ry
deve essere pari almeno a:
"=
2
− $ = 5.5' ℎ)
2
Se Ry è troppo bassa, il circuito non sarà in grado di oscillare in quanto i componenti attivi dell’operazionale
sarebbero in una condizione di saturazione.
A livello sperimentale si ottiene che il minimo valore di Ry affinché si ottenga un segnale sinusoidale è:
" = 6.1' ℎ)
Tale valore è accettabile in quanto rispetta la condizione di oscillazione teorica e, tenendo conto dei vari disturbi ed
errori di cui è necessario tener conto, possiamo anche considerarlo una conferma del valore teorico di Ry. Un
ulteriore conferma ci viene data avviando la simulazione del circuito in ambiente software Pspice. Difatti
introducendo un valore parametrico di Ry si ha che aumentando il valore di Ry nel tempo, si ottiene la seguente
curva di risposta:
E’ possibile notare che, inizialmente, quando il valore di Ry è troppo basso e non in grado di rispettare la condizione
di oscillazione, in uscita non si ottiene alcun segnale. All’aumentare di Ry si ottiene un segnale di tipo oscillatorio e
man mano che la condizione di oscillazione viene confermata, il segnale tende a somigliare sempre più ad una
perfetta sinusoide.
Per quanto riguarda la Vo, si ottiene dalla formula teorica:
+,
= 10 = 20 . .
Questo valore è ottenuto nella condizione in cui si pone Ry=5.5Kohm cioè nel caso limite che verifica la condizione di
oscillazione. Il valore ottenuto sperimentalmente con Ry=6.1Kohm si avvicina molto a tale valore per cui la relazione
è verificata.
Stesso discorso vale per la frequenza di oscillazione. Difatti teoricamente si ottiene:
=
2
1
= 3.386'
I valori sperimentali ci dicono che il periodo del segnale sinusoidale di uscita vale circa:
1 = 0.3)2
Essendo T=1/f, si ottiene che sperimentalmente la frequenza del segnale di uscita è:
=
1
103 = 3.3'
0.3
Questo valore introduce un errore di soli 86Hz dal valore teorico per cui anche in questo caso possiamo confermare
che il valore teorico è confermato dalla verifica pratica.
Conclusioni:
Attraverso questa esercitazione è stato possibile verificare come in effetti, affinché un circuito oscillatore generi in
uscita dei segnali sinusoidali persistenti devono essere verificate le condizioni di oscillazione derivate dal principio
generale di Barkhausen. Nel nostro caso, si è potuto osservare che solo in corrispondenza di un determinato valore
di Ry, il circuito restituiva in uscita un segnale sinusoidale. Ciò avveniva in corrispondenza di un valore di Ry tale che
R1=Rx+Ry rispettasse la condizione di oscillazione:
2≥2 1
Nei circuiti pratici come abbiamo visto è necessario introdurre delle reti elettriche in grado di mantenere
costantemente il prodotto GH uguale all’unità. Per far questo si utilizzando termistori NTC o PTC in modo tale che
sostituendoli al posto di R2 o R1 si possa controllare e stabilizzare il guadagno in uscita. Se si utilizzasse un PTC al
posto di R1, all’aumentare dell’ampiezza del segnale di uscita, aumenterebbe la corrente che percorre il termistore.
Di conseguenza questi aumenterebbe la sua resistenza e di conseguenza il guadagno in uscita sarebbe attenuato.
Viceversa una diminuzione dell’ampiezza provocherebbe la diminuzione del valore di resistenza del PTC e dunque il
guadagno aumenterebbe . In questo modo l’ampiezza del segnale di uscita è mantenuta costante e stabile nel
tempo.