Teoremi di geometria piana dimostrati con notazione semplificata per fini didattici
di Luciano Porta
Tradizionalmente nella scuola secondaria di primo grado sono dimostrati solo il teorema di Pitagora, quelli
di Euclide sul triangolo rettangolo e, talvolta quello di Talete. Penso che anche altri teoremi sui triangoli, sui
quadrilateri e sul cerchio possano essere affrontati, purché si usino notazioni semplificate, anche se non
convenzionali e formalmente non del tutto corrette, per non distogliere l’attenzione dal ragionamento.
Inoltre penso che si possano già utilizzare alcuni teoremi per dimostrarne “a catena” altri fornendo così agli
studenti un esempio significativo di come lavori un matematico. Non nego ovviamente l’importanza di
scoprire in modo induttivo le proprietà delle figure geometriche, misurando lati, angoli e diagonali,
ritagliando o piegando figure di carta e utilizzando un software di geometria dinamica: queste attività
laboratoriali devono precedere la dimostrazione e il docente non deve fornire la spiegazione “già pronta”,
ma deve guidare gli studenti. Gli argomenti proposti non devono essere affrontati consecutivamente.
Uguaglianza degli angoli opposti al vertice (attribuito a Talete)
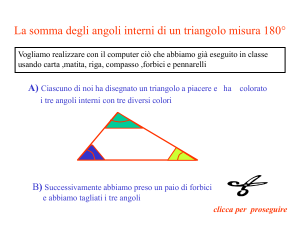
La somma degli angoli interni di un triangolo è un angolo piatto (attribuito alla scuola pitagorica)
In un triangolo isoscele gli angoli adiacenti alla base sono uguali
1
In un parallelogrammo i lati opposti sono uguali e gli angoli opposti sono uguali
In un parallelogrammo le diagonali si dividono reciprocamente a metà
In un rettangolo le diagonali sono uguali
In un trapezio isoscele gli angoli adiacenti alla base maggiore (o minore) sono uguali
2
In un trapezio isoscele le diagonali sono uguali
In un rombo le diagonali sono perpendicolari
Il diametro è la corda maggiore
I segmenti di tangente condotti da un punto esterno ad una circonferenza sono uguali
3
L’angolo al centro è il doppio di quello alla circonferenza che insiste sullo stesso arco
Possono presentarsi quattro situazioni: ciascuna deve essere dimostrata separatamente, anche se la
dimostrazione della seconda deve essere applicata per dimostrare il terzo e il quarto caso.
Situazione 1 (è una situazione molto particolare)
Situazione 2 (è la situazione base)
Situazione 3
4
Situazione 4
Gli angoli alla circonferenza che insistono sullo stesso arco sono uguali
In un quadrilatero inscritto la somma degli angoli opposti è di un angolo piatto
5
In un quadrilatero circoscritto la somma dei lati opposti è uguale
www.webalice.it/lucianoporta i Pitagorici DIDATTICA E DIVULGAZIONE DELLA MATEMATICA E DELLE SCIENZE LEZIONI TRE
6