Nessun titolo diapositiva

STRUTTURA INTERNA DELLA TERRA
MAPPA SISMICA MONDIALE
MAPPA SISMICA EUROPEA
EFFETTI PRINCIPALI DEL TERREMOTO
- Scuotimento del terreno
- Apertura di faglie e fratture in superficie
- Cedimenti del terreno (liquefazione)
- Maremoti / Tsunami
SCUOTIMENTO DEL TERRENO - Accelerogramma
0.45
0.4
0.35
0.3
0.25
A cceleration [g]
0.2
0.15
0.1
0.05
0
- 0.05
- 0.1
- 0.15
- 0.2
- 0.25
- 0.3
0
1
2
3
4
5
6
7
8
9
10
11
Time [s ec]
12
13
14
15
16
17
18
19
20
SCUOTIMENTO DEL TERRENO – Onde Sismiche
SCUOTIMENTO DEL TERRENO – Onde Sismiche
Onde di profondità
Onde di superficie
Onde di Rayleigh
Onde P
Onde S
Onde di Love
LE FAGLIE
LE FAGLIE
LE FAGLIE – La Faglia di S.Andrea
IL FENOMENO DELLA LIQUEFAZIONE
Prende il nome di liquefazione un cedimento del suolo dovuto allo scuotimento di sedimenti sabbiosi
saturi in acqua che assumono comportamento da liquido.
Perché avvenga liquefazione è necessario che i singoli granuli di sabbia perdano il contatto reciproco:
essendo il continuo della sostanza ora liquido, il sedimento si metterà a fluire come un liquido viscoso.
Lo scuotimento indotto da un terremoto può provocare la liquefazione di sedimenti sabbiosi saturi in
acqua, allorquando questi siano confinati da strati meno permeabili.
CATEGORIA DEL SUOLO
Per sottosuoli appartenenti alle ulteriori categorie S1 ed S2 di seguito indicate, è necessario predisporre
specifiche analisi per la definizione delle azioni sismiche, particolarmente nei casi in cui la presenza di
terreni suscettibili di liquefazione e/o di argille d’elevata sensitività possa comportare fenomeni di collasso
del terreno.
Categoria del
suolo
Descrizione
S1
Depositi di terreni caratterizzati da valori di VS,30 inferiori a 100 m/s (ovvero
10 < Cu,30 < 20 kPa), che includono uno strato di almeno 8 m di terreni a
grana fina di bassa consistenza, oppure che includono almeno 3 m di torba
o di argille altamente organiche.
S2
Depositi di terreni suscettibili di liquefazione, di argille sensitive o qualsiasi
altra categoria di sottosuolo non classificabile nei tipi precedenti.
IL FENOMENO DELLA LIQUEFAZIONE
Per liquefazione di un terreno s'intende il quasi totale annullamento della sua resistenza al taglio con
l'assunzione del comportamento meccanico caratteristico dei liquidi. I fenomeni di liquefazione che
interessano i depositi sabbiosi saturi dipendono da:
• proprietà geotecniche dei terreni
• caratteristiche delle vibrazioni sismiche e loro durata
• genesi e storia geologica dei terreni
• fattori ambientali
Particelle di terreno saturo
Particelle di terreno
liquefatto
IL FENOMENO DELLA LIQUEFAZIONE
Durante una sollecitazione sismica vengono indotte nel terreno delle sollecitazioni cicliche di taglio,
mentre la pressione litostatica, dovuta al peso dei sedimenti sovrastanti, resta costante.
Nel terreno si possono generare fenomeni di liquefazione se la scossa sismica produce un numero di
cicli tale da far si che la pressione interstiziale uguagli la pressione di confinamento. Nei depositi
la pressione di confinamento aumenta con la profondità, mentre l'ampiezza dello sforzo di taglio indotto
dal sisma diminuisce. La resistenza alla liquefazione quindi è maggiore con la profondità.
Quindi, maggiore è la durata di un terremoto più alta è la possibilità che si arrivi (maggior numero di
cicli) alla liquefazione. Inoltre, maggiore è l'ampiezza della vibrazione e della deformazione indotta e
minore è il numero di cicli necessari per giungere a tale condizione.
La probabilità che un deposito raggiunga le condizioni per la liquefazione dipende anche dallo stato di
addensamento, dalla composizione granulometrica, dalle condizioni di drenaggio, dalla storia delle
sollecitazioni sismiche e dall'età del deposito stesso. Tanto minore è il grado di addensamento del
materiale (elevato indice dei vuoti e bassa densità relativa) tanto maggiore è la probabilità che, a parità
di altre condizioni, un deposito raggiunga lo stato di liquefazione.
Per quanto riguarda la storia delle sollecitazioni sismiche su un deposito si può affermare che
precedenti deformazioni moderate influiscano positivamente sulla resistenza del deposito, mentre
una storia caratterizzata da alti livelli di deformazione (deposito già soggetto a liquefazione) ha effetti
negativi sul potenziale di riliquefazione. I depositi sabbiosi con più alto potenziale di liquefazione sono i
più recenti. A parità di composizione e di altre condizioni lo stesso deposito, se più antico, avrà
sviluppato legami intergranulari e cementazioni sempre più forti con il tempo. Inoltre la struttura di un
deposito antico sarà resa più stabile e omogenea per gli effetti delle vibrazioni indotte da precedenti
terremoti di piccola entità.
IL FENOMENO DELLA
LIQUEFAZIONE
Mappa del Rischio
IL FENOMENO DELLA LIQUEFAZIONE
Effetti della Liquefazione
IL FENOMENO DELLA LIQUEFAZIONE
Espansione laterale (lateral spread)
IL FENOMENO DELLA LIQUEFAZIONE
Espansione laterale (lateral spread)
IL FENOMENO DELLA LIQUEFAZIONE
Perdita di portanza (loss of bearing strength)
IL FENOMENO DELLA LIQUEFAZIONE
Perdita di portanza (loss of bearing strength)
TSUNAMI
TSUNAMI
TSUNAMI
L'energia di uno tsunami è costante, in funzione della sua altezza e velocità. Quindi, quando l'onda si
avvicina alla terra, la sua altezza aumenta mentre diminuisce la sua velocità. Le onde viaggiano a velocità
elevate, più o meno senza essere notabili quando attraversano le acque profonde, ma la loro altezza può
crescere fino a 30 metri e più quando raggiungono la linea costiera.
TSUNAMI
La velocità del maremoto può essere semplicemente espressa dalla formula:
dove g è l'accelerazione di gravità e vale 9,8 m/s2, e h è la profondità del mare espressa in
metri.
TSUNAMI
TSUNAMI
RISCHIO SISMICO
S. Giuliano di Puglia (CB), 31 ottobre 2002
RISCHIO SISMICO
Epicentro del 31 ottobre 2002
Terremoti storici nell’area interessata
RISCHIO SISMICO
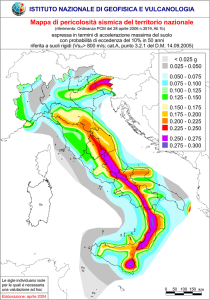
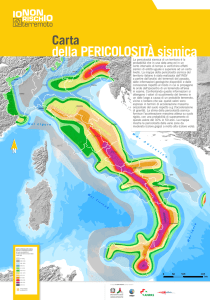
Mappa sismica precedente
Mappa sismica nuova
MAPPA SISMICA
1984
1a Categoria
2a Categoria
3a Categoria
Non sismica
MAPPA SISMICA
2003
MACRO ZONAZIONE E MICRO ZONAZIONE SISMICA
MACRO ZONAZIONE SISMICA
MICRO ZONAZIONE SISMICA
La Microzonazione sismica rappresenta l’attività svolta ai fini di una più dettagliata suddivisione del territorio in aree in cui i
valori di pericolosità sismica rispecchiano più rigorosamente le condizioni locali. L’analisi della risposta di un suolo alle
sollecitazioni sismiche (Risposta Sismica Locale), costituisce la parte fondamentale delle attività di Microzonazione Sismica.
MAPPE SISMICHE
Mappa Sismica 2008 – Reticolo di riferimento
NORME TECNICHE PER LE COSTRUZIONI
Mappa Sismica 2008 – Reticolo di riferimento
NORME TECNICHE PER LE COSTRUZIONI
Mappa Sismica 2008 – Reticolo di riferimento
MODELLI DI CALCOLO STRUTTURALE
IMPALCATI RIGIDI O DEFORMABILI
MODELLI DI CALCOLO STRUTTURALE
IMPALCATI RIGIDI O DEFORMABILI
Modello strutturale ad impalcato rigido
MODELLI DI CALCOLO STRUTTURALE
IMPALCATI RIGIDI O DEFORMABILI
Modello strutturale ad impalcato deformabile
IMPALCATI RIGIDI O DEFORMABILI
Schema telaio
IMPALCATI RIGIDI O DEFORMABILI
Deformata del telaio: Quota 3 = Piano Rigido
IMPALCATI RIGIDI O DEFORMABILI
Diagramma del Momento Flettente del telaio: Quota 3 = Piano Rigido
IMPALCATI RIGIDI O DEFORMABILI
Diagramma del Taglio del telaio:
Quota 3 = Piano Rigido
IMPALCATI RIGIDI O DEFORMABILI
Deformata del telaio: Quota 3 = Piano Deformabile
IMPALCATI RIGIDI O DEFORMABILI
Diagramma del Momento Flettente del telaio:
Quota 3 = Piano Deformabile
IMPALCATI RIGIDI O DEFORMABILI
Diagramma del Taglio del telaio:
Quota 3 = Piano Deformabile
IMPALCATI RIGIDI O DEFORMABILI
Deformata
Piano Rigido
Piano Deformabile
IMPALCATI RIGIDI O DEFORMABILI
Diagramma del Momento Flettente
Piano Rigido
Piano Deformabile
IMPALCATI RIGIDI O DEFORMABILI
Diagramma del Taglio
Piano Rigido
Piano Deformabile
CRITERI GENERALI DI PROGETTAZIONE (D.M. 2008)
In ragione della necessità che la costruzione sia dotata di sistemi strutturali capaci, con costi
accettabili, di soddisfare i requisiti di sicurezza nei confronti sia dei carichi verticali che dell’azione
sismica, in siti a sismicità significativa i criteri di progettazione nei confronti delle azioni sismiche devono
essere considerati già nell’impostazione della progettazione strutturale.
La costruzione deve essere dunque dotata di sistemi resistenti lungo almeno due direzioni e capaci di
garantire un’adeguata resistenza e rigidezza nei confronti sia dei moti traslazionari, sia dei moti
torsionali dovuti all’eccentricità tra il centro di massa ed il centro di rigidezza dell’intera struttura o anche
solo di una sua porzione.
Tali moti torsionali tendono a sollecitare i diversi elementi strutturali in maniera non uniforme. A tal fine,
sono da preferirsi configurazioni strutturali in cui i principali elementi resistenti all’azione sismica
sono distribuiti nelle zone periferiche della costruzione e al contempo limitano l’eccentricità tra
centro di massa e centro di rigidezza a ciascun livello della costruzione. Per massimizzare la rigidezza
torsionale conseguita nel modo suddetto è necessario che gli orizzontamenti funzionino da diaframma
rigido ai fini della ripartizioni delle forze sugli elementi verticali che li sostengono, nei modi specificati al
Cap. 7.2.6 delle Norme Tecniche per le Costruzioni.
MODELLAZIONE STRUTTURALE
Schema ERRATO – Plinti non collegati
MODELLAZIONE STRUTTURALE
Schema CORRETTO – Plinti collegati
MODELLAZIONE STRUTTURALE
Schema ERRATO – Pilastri orientati secondo il lato della struttura più
resistente
MODELLAZIONE STRUTTURALE
Schema CORRETTO – Pilastri orientati secondo il lato della struttura meno
resistente
MODELLAZIONE STRUTTURALE
Schema ERRATO – Modello strutturale a telai non collegati
MODELLAZIONE STRUTTURALE
Schema CORRETTO – Modello strutturale a telai collegati
MODELLAZIONE STRUTTURALE
Schema SCONSIGLIATO – Distribuzione irregolare delle pareti
MODELLAZIONE STRUTTURALE
Schema CONSIGLIATO – Distribuzione regolare delle pareti
ANALISI SISMICA DELLE STRUTTURE
Baricentro delle Masse e delle Rigidezze
ANALISI SISMICA DELLE STRUTTURE
Baricentro delle Masse e delle Rigidezze
Struttura 1
Struttura 2
ANALISI SISMICA DELLE STRUTTURE
Baricentro delle Masse e delle Rigidezze
Struttura 1
Struttura 2
ANALISI SISMICA DELLE STRUTTURE
Posizione del Baricentro delle Rigidezze
s  u 0    yi , xi 
Spostamento globale del singolo
elemento
ui  u0 x    yi
vi  u0 y    xi
Traslazione e rotazione dell’impalcato rigido
Componenti dello spostamento globale
ANALISI SISMICA DELLE STRUTTURE
Posizione del Baricentro delle Rigidezze
K ix 
12  E  I x
h3
K iy 
12  E  I y
h3
Rigidezza del singolo elemento
Fxi  Ki u0 x    yi   Kix  u0 x    K xi  yi
Fyi  Ki u0 y    xi   Kiy  u0 y    K yi  yi
Aliquota della forza tagliante di piano che sopporta il singolo elemento
FxT   Kix  u0 x     Kix  yi
FyT   Kiy  u0 y     Kiy  xi
Forza tagliante di piano totale
ANALISI SISMICA DELLE STRUTTURE
Posizione del Baricentro delle Rigidezze
YR
K y


K
xi
i
xi
XR
K x


K
yi
i
yi
Coordinate del baricentro delle rigidezze dell’impalcato
ANALISI SISMICA DELLE STRUTTURE
Posizione del Baricentro delle Rigidezze
ANALISI SISMICA DELLE STRUTTURE
Posizione del Baricentro delle Rigidezze
ANALISI SISMICA DELLE STRUTTURE
Posizione del Baricentro delle Rigidezze
ANALISI SISMICA DELLE STRUTTURE
Posizione del Baricentro delle Rigidezze
CORREZIONE TORSIONALE
VECCHIA NORMA - D.M. ‘96
A/B > 2.5
Analisi Sismica Statica
CORREZIONE TORSIONALE
Metodo dell’incremento dell’eccentricità (5% di “d”)
.
CORREZIONE TORSIONALE
Metodo del coefficiente
d
d  1  0.6  x / Lc
Per edifici aventi massa e rigidezza distribuite in modo simmetrico in pianta.
MODELLAZIONE STRUTTURALE
1 – Sbalzi
2 – Pilastri in falso
3 – Luci elevate
4 – Travi a spessore
Modellazioni sconsigliate
ANALISI SISMICA DELLE STRUTTURE
- Analisi sismica Lineare
- Analisi sismica Non Lineare
- Analisi sismica Statica classica
- Analisi sismica Dinamica classica
- Analisi sismica Statica nodale
- Analisi sismica Dinamica nodale
ANALISI SISMICA DELLE STRUTTURE
Analisi Sismica Classica
Analisi Sismica Nodale
L’EFFETTO DEL SISMA SULLE STRUTTURE
le azioni dinamiche agenti nella struttura dovute all’accelerazione delle masse
F (t )  m  a(t )  var iabile
vengono sostituite da azioni statiche equivalenti
F  cos t
Ipotesi Fondamentali:
- Nella pratica professionale non è necessario conoscere l’andamento nel tempo delle
caratteristiche di sollecitazione in ogni sezione dell’elemento strutturale, ma è sufficiente
conoscerne il valore massimo.
- Nelle strutture tipiche dell’ingegneria civile (ad esempio edifici per civile abitazione) le masse
strutturali sono concentrate in massima parte in corrispondenza degli impalcati (solai).
- In alcuni casi (edifici in c.a.) gli impalcati possono essere considerati elementi indeformabili
nel proprio piano, e quindi in grado di connettere rigidamente tutti i nodi strutturali giacenti su
di essi.
L’EFFETTO DEL SISMA SULLE STRUTTURE
Se si impone alla testa del piedritto uno spostamento
orizzontale u0 (rispetto la posizione di riposo verticale) e
successivamente lo si lascia libero, sul sistema si instaurerà
un regime di oscillazioni libere caratterizzate da una
andamento sinusoidale nel tempo con un periodo di
oscillazione T0, questo è il tempo che intercorre per
permettere al traverso di compiere un’oscillazione completa e
ritornare nella posizione iniziale. Tale periodo, detto anche
periodo proprio dell’oscillatore è legato alle due grandezze m
e k (massa e rigidezza) dalla seguente relazione:
T0  2   
m
k
L’EFFETTO DEL SISMA SULLE STRUTTURE
Oscillazione ideale
(smorzamento nullo)
Oscillazione reale
(smorzamento non nullo)
L’EFFETTO DEL SISMA SULLE STRUTTURE
L’effetto del sisma sulla struttura può essere considerato come l’applicazione al sistema di una
forza di tipo sinusoidale
 2  
F (t )  F  sin  t   F  sin
t 
T


L’applicazione di questa forza instaurerà sul sistema un regime di oscillazioni forzate il quale,
dopo una prima fase iniziale in cui saranno presenti anche le oscillazioni libere smorzate,
assumerà un forma analoga a quella delle oscillazioni libere ma con un periodo che adesso
sarà quello della forzante, con uno sfasamento rispetto ad essa ed un’ampiezza delle
oscillazioni che dipende dal rapporto F/k (F = valore massimo della forza, k = rigidezza del
sistema) e dal rapporto dei due periodi a = T0/T (T0 = periodo di vibrazione del sistema; T =
periodo di oscillazione della forza). Tale dipendenza è espressa dalla relazione seguente:
u (t ) 
1
(1  a 2 ) 2  4   2  a 2

F
F
 sin  t    A   sin  t  
K
K
L’EFFETTO DEL SISMA SULLE STRUTTURE
.
Caso 1
( = 0 ; a = 1)
Smorzamento nullo e periodo della forzante uguale al
periodo proprio della struttura, condizione detta di
“risonanza” (condizione teorica).
Caso 2
( piccolo ; a = 1)
Smorzamento piccolo e periodo della forzante
uguale al periodo proprio della struttura.
L’amplificazione è grande, ma ha valore finito.
Caso 3
(a = 0)
Periodo della forzante molto più grande del periodo
proprio della struttura. La massa segue la forza
come se si trattasse di tante condizioni statiche in
sequenza.
Caso 4
(a grande)
Periodo della forzante molto più piccolo del periodo
proprio della struttura. Il sistema oscillante, poiché la
variazione della forzante e molto rapida, non risente
dell’effetto, comportandosi come se questa non
fosse presente.
L’EFFETTO DEL SISMA SULLE STRUTTURE
L’EFFETTO DEL SISMA SULLE STRUTTURE
.
mut  cu  ku  0
m  ug  u  cu  ku  0
mu  cu  ku  mug  Peq
TIPI DI ANALISI SISMICA
Analisi Sismica Statica - D.M. ‘96
Fi  Wi  C    RT    I   i
Wi = massa del piano i-esimo dell’edificio
C = coefficiente di intensità sismica
 = coefficiente di struttura
R (T) = coefficiente di risposta
 = coefficiente di fondazione
I = coefficiente di protezione sismica
n
i = coefficiente di distribuzione
 i  hi 
W
j 1
n
W
j 1
j
j
 hj
TIPI DI ANALISI SISMICA
Analisi Sismica Statica – Norme Tecniche 2008
Fi  Fh
Fh 
S d (T1 ) W  
g
zi Wi
 z j W j
zi , zj = altezze dei piani i-esimo e j-esimo dalla fondazione
Wi, Wj = pesi delle masse ai piani i-esimo e j-esimo
Sd(T1) = ordinata dello spettro di progetto in corrispondenza del valore T1 del periodo
T1  C1  H 3 / 4
H = altezza dell’edificio, espressa in metri, a partire dal piano di fondazione
Cl = coefficiente funzione della tipologia strutturale
W = peso complessivo della struttura
TIPI DI ANALISI SISMICA
Analisi Sismica Statica - Distribuzione delle
forze sismiche equivalenti sulla struttura
.
TIPI DI ANALISI SISMICA
Analisi Sismica Dinamica
1) Determinazione dei modi di vibrare della costruzione (analisi
modale).
Modo n.1
2) Calcolo degli effetti dell’azione sismica, rappresentata dallo
spettro di risposta di progetto, per ciascuno dei modi di vibrare
individuati.
3) Combinazione degli effetti relativi a ciascun modo di vibrare.
Modo n.3
Schema Strutturale
Modo n.7
TIPI DI ANALISI SISMICA
Analisi Sismica Dinamica
L’utilizzo dello spettro di risposta consente di calcolare gli effetti massimi del terremoto sulla costruzione associati a
ciascun modo di vibrare. Poiché durante il terremoto, tuttavia, gli effetti massimi associati ad un modo di vibrare non si
verificano generalmente nello stesso istante in cui sono massimi quelli associati ad un altro modo di vibrare, tali effetti non
possono essere combinati tra di loro mediante una semplice somma ma con specifiche regole di combinazione, di natura
probabilistica, che tengono conto di questo sfasamento temporale.
STot  S12  S22  ...  Sn2
n
n
n
S   S  
2
i 1
2
i
i 1
Si  S j
2
j 1 1   ij
Radice della somma dei quadrati (SRSS)
Combinazione Quadratica Completa (CQC)
TIPI DI ANALISI SISMICA
Analisi Sismica Dinamica
m partec.mod o  5%
m
i  eff
mtot
 0.85
TIPI DI ANALISI SISMICA
Analisi Sismica Dinamica - Distribuzione delle
forze sismiche equivalenti sulla struttura
.
CRITERI DI SCELTA DEL TIPO DI ANALISI
SISMICA
Requisito primario di applicabilità dell’analisi sismica statica è la regolarità
della struttura.
regolarità geometrica in pianta: intendendo con essa sia la regolarità geometrica
della pianta i cui elementi strutturali devono essere posti a distanze regolari, e sia la
regolarità della distribuzione delle rigidezze (ossia delle inerzie) degli stessi
elementi.
regolarità in elevazione: intesa come la proprietà da parte di tutti gli elementi
verticali che abbiano resistenza significativa all’azione sismica di estendersi senza
interruzione dalle fondazioni fino alla sommità dell’edificio, mantenendosi il rapporto
tra masse e rigidezze degli impalcati pressoché costante per tutta l’altezza.
distribuzione regolare dei pesi e dei carichi: assenza quindi di pannelli di
tamponamento, o di carichi sia permanenti che accidentali distribuiti sugli impalcati
in maniera asimmetrica.
CRITERI DI SCELTA DEL TIPO DI ANALISI
SISMICA
REQUISITO DI APPLICABILITA’ DELL’ANALISI
SISMICA STATICA (D.M. ‘96)
T1  0.1
H
 1.4 sec
B
H = massima altezza dell’edificio a partire dal piano di fondazione
B = massima dimensione in pianta dell’edificio
CRITERI DI SCELTA DEL TIPO DI ANALISI
SISMICA
REQUISITO DI APPLICABILITA’ DELL’ANALISI
SISMICA STATICA (Norme Tecniche 2005)
T1  C1  H 3 / 4  2.5  TC
H = massima altezza dell’edificio a partire dal piano di fondazione
Cl = coefficiente moltiplicativo funzione della tipologia strutturale, il
cui valore è riportato nel prospetto seguente:
C1 = 0.085
per edifici con struttura a telaio in acciaio
C1 = 0.075
per edifici con struttura a telaio in calcestruzzo
C1 = 0.050
per edifici con qualsiasi altro tipo di struttura
SPETTRO DI RISPOSTA ELASTICO
.
2 
4  2
S a (To ,  ) 
 Sv (To ,  )  2  S De (To ,  )
To
T0
T02
Feq  k  S De (To ,  )  k 
 S a (To ,  )
4  2
T0  2   
m
k
Feq  m  Sa (To ,  )
SPETTRO DI RISPOSTA ELASTICO
Si può diagrammare il valore della
massima accelerazione ottenendo
lo spettro di risposta
dell’accelerogramma
a/g
1
0.5
0
0
1
2
T
Si può quindi definire una curva che inviluppa tutti gli spettri di risposta, o che viene superata solo
occasionalmente
3s
SPETTRO DI RISPOSTA ELASTICO
CATEGORIA DEL SUOLO
.
SPETTRO DI PROGETTO
CONFINAMENTO DELLE SEZIONI IN C.A.
In genere per la progettazione delle sezione in c.a. si assume un valore di deformazione ultima del
calcestruzzo cu = 0.35 % pari a quello del calcestruzzo non confinato. Nel caso del calcolo delle
curvature ultime ai fini della valutazione della capacità rotazionale da usare nelle analisi non lineari
questa ipotesi risulta troppo lontana dalla realtà fisica ed è necessario valutare in maniera più raffinata
la reale capacità deformativa del calcestruzzo in funzione del grado di confinamento.
CONFINAMENTO DELLE SEZIONI IN C.A.
Comportamento di elementi confinati e non confinati.
CONFINAMENTO DELLE SEZIONI IN C.A.
Distacco del copriferro dovuto a staffatura insufficiente.
CONFINAMENTO DELLE SEZIONI IN C.A.
Corretta staffatura di un pilastro in c.a..
CONFINAMENTO DELLE SEZIONI IN C.A.
Rottura diagonale per taglio di un nodo trave-pilastro non confinato.
CONFINAMENTO DELLE SEZIONI IN C.A.
Rottura diagonale per taglio di un nodo trave-pilastro non confinato.
CONFINAMENTO DELLE SEZIONI IN C.A.
Espulsione del copriferro e deformazione delle armature longitudinali di
un nodo trave-pilastro non confinato.
CONFINAMENTO DELLE SEZIONI IN C.A.
Espulsione del copriferro e deformazione delle armature longitudinali di
un nodo trave-pilastro non confinato.
CONFINAMENTO DELLE SEZIONI IN C.A.
Espulsione del copriferro e deformazione delle armature longitudinali di
un nodo trave-pilastro non confinato.