ESERCITAZIONE DI LABORATORIO
SULLA DETERMINAZIONE DELLA RISPOSTA IN FREQUENZA
DI UN FILTRO PASSIVO PASSA-BASSO
COSTITUITO DA UNO STADIO RC
Premessa
Un filtro è un quadripolo capace di operare una selezione, tra i segnali applicati in ingresso, in funzione della
& ( f ) il rapporto tra il fasore rappresentativo della tensione
frequenza; per un filtro possiamo definire Attenuazione A
in uscita ed il fasore rappresentativo della tensione in ingresso.
V& ( f )
A& ( f ) = o
V&i ( f )
FILTRO
fig. 1
Le misure principali che si eseguono su di un filtro sono:
•
& ( f ) del segnale in uscita, rispetto a quello in ingresso, in
rilievo del modulo della attenuazione A = A
funzione della frequenza, il modulo viene espresso in dB:
A& ( f )
•
dB
= 20 ⋅ log(Vo Vi ) ;
& ( f ) del segnale in uscita, rispetto a quello in ingresso, in funzione della
rilievo dello sfasamento ∠A
frequenza.
I filtri passivi si distinguono, in funzione della loro risposta in frequenza in:
Filtri passa-basso;
Filtri passa-banda;
Filtri passa-alto;
Filtri escludi banda.
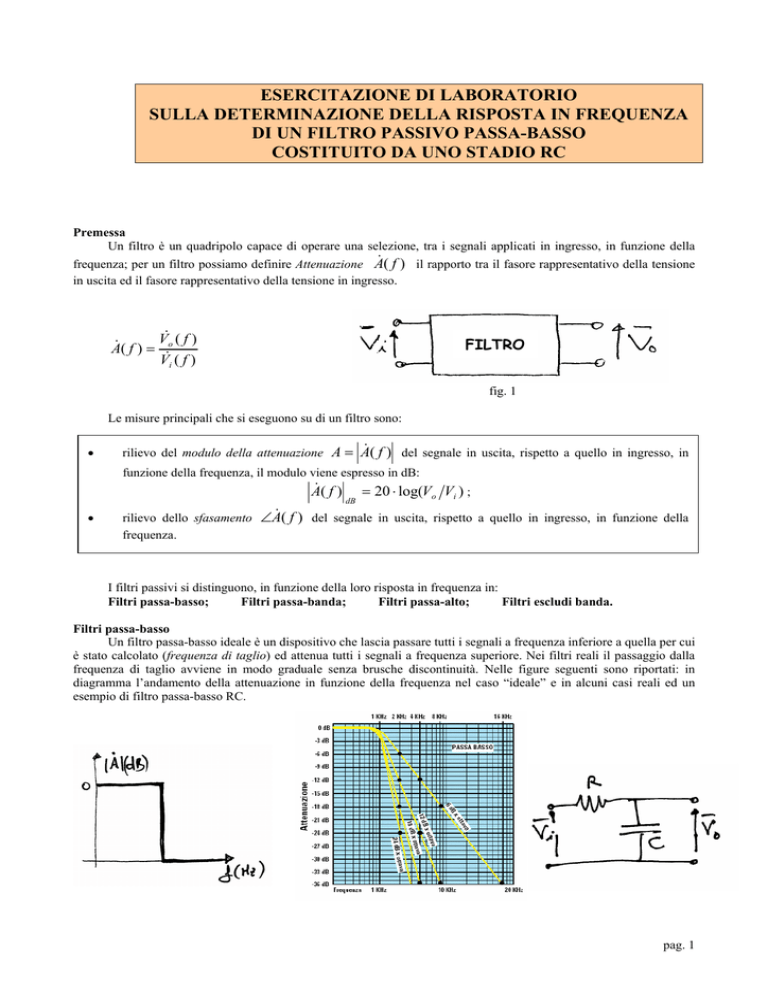
Filtri passa-basso
Un filtro passa-basso ideale è un dispositivo che lascia passare tutti i segnali a frequenza inferiore a quella per cui
è stato calcolato (frequenza di taglio) ed attenua tutti i segnali a frequenza superiore. Nei filtri reali il passaggio dalla
frequenza di taglio avviene in modo graduale senza brusche discontinuità. Nelle figure seguenti sono riportati: in
diagramma l’andamento della attenuazione in funzione della frequenza nel caso “ideale” e in alcuni casi reali ed un
esempio di filtro passa-basso RC.
pag. 1
Filtri passa-alto
Un filtro passa-alto ideale è un dispositivo che lascia passare tutti i segnali a frequenza superiore a quella per cui
è stato calcolato (frequenza di taglio) ed attenua tutti i segnali a frequenza inferiore. Nei filtri reali il passaggio dalla
frequenza di taglio avviene in modo graduale senza brusche discontinuità. Nelle figure seguenti sono riportati: in
diagramma l’andamento della attenuazione in funzione della frequenza nel caso “ideale” e in alcuni casi reali ed un
esempio di filtro passa-alto RC.
Filtri passa-banda
Un filtro passa-basso ideale è un dispositivo che lascia passare tutti i segnali compresi in un intervallo di
frequenze delimitato da una frequenza di taglio inferiore ed una frequenza di taglio superiore a quella per cui è stato
calcolato (frequenza di taglio) ed attenua tutti i segnali a frequenza superiore. Nei filtri reali il passaggio dalle frequenze
di taglio avviene in modo graduale senza brusche discontinuità. Nelle figure seguenti sono riportati: in diagramma
l’andamento della attenuazione in funzione della frequenza nel caso “ideale” e in un caso reale.
Filtri escludi-banda
Un filtro escludi-banda ideale è un dispositivo che lascia passare tutti i segnali non compresi in un intervallo di
frequenze delimitato da una frequenza di taglio inferiore ed una frequenza di taglio superiore per cui è stato calcolato
ed attenua tutti i segnali compresi nell’intervallo di frequenza. Nei filtri reali il passaggio dalle frequenze di taglio
avviene in modo graduale senza brusche discontinuità. Nelle figure seguenti sono riportati: in diagramma l’andamento
della attenuazione in funzione della frequenza nel caso “ideale” e in un caso reale.
pag. 2
Analisi del filtro passivo passa-basso costituito da uno stadio RC
Il circuito oggetto della prova è di seguito riportato, dall’analisi del circuito risulta:
V&i
1
⋅
⇒
jωC1 ( R + 1 )
1
jωC1
V&
1
da cui
A& = o =
&
V 1 + jωR C
V&o =
1
i
1
fig. 2
A = A& =
1
1 + (ωR1C1 )
2
∆ϕ = ∠A& ( f ) = − arctg (ωR1C1 )
La frequenza di taglio ft del filtro è quella in corrispondenza della quale la potenza trasmessa si dimezza e quindi
il modulo della attenuazione assume valore:
V
1
A& = o =
= 0,707
Vi
2
nel caso in esame, essendo R1 = 10 kΩ e C1 = 47 nF
⇒
⇒
ft =
1
2πR1C1
ft ≅ 340 Hz
& ( f ) , espresso in dB A& ( f )
Il modulo della attenuazione A = A
dB
= 20 ⋅ log(Vo Vi ) , è di seguito
rappresentato in funzione della frequenza; si osserva che in corrispondenza della frequenza di taglio (ft ≅ 340 Hz)
l’attenuazione assume il valore –3 dB .
& ( f ) = − arctg (ωR C ) del segnale in uscita, rispetto a quello in ingresso, è di
Lo sfasamento ∆ϕ = ∠A
1 1
seguito rappresentato in funzione della frequenza; si osserva che in corrispondenza della frequenza di taglio (ft ≅ 340
Hz) lo sfasamento assume il valore ∆ϕ = – 45° (π/4).
fig. 3
fig. 4
Progetto del circuito di misura e scelta degli strumenti
Il circuito oggetto della prova è realizzato con:
•
un resistore in pasta di valore nominale R1 = 10 kΩ, potenza massima 0,25 W, tolleranza: ± 5%: è quindi
applicabile al massimo una d.d.p. pari a:
V = P ⋅ R = 0,25 ⋅ 10 ⋅ 10 3 = 50V ;
pag. 3
un condensatore in poliestere di capacità C1 = 47 nF, tolleranza: ± 5%, tensione massima 200 V.
Il circuito di misura prevede un generatore di forme d’onda per produrre la tensione sinusoidale in ingresso Vi,
un frequenzimetro per la misura della frequenza ed un’oscilloscopio digitale per la misura dei livelli di tensione in
ingresso ed in uscita e per la misura del ritardo ∆t del segnale in uscita rispetto al segnale in ingresso; quest’ultima
misura, nota la frequenza f, consente la determinazione dello sfasamento ∆ϕ = ω ⋅ ∆t = 2πf ⋅ ∆t , dove ∆t è il ritardo
temporale tra tensione in ingresso e tensione in uscita (come indicato in fig. 6). Allo scopo di facilitare la misura di ∆t e
contemporaneamente ridurre le incertezze di misura, è opportuno “dilatare” la scala dei tempi solo per la misura di ∆t.
Lo schema del circuito di misura è di seguito riportato:
•
Generatore di funzioni
Hz
Frequenzimetro
Hz
Oscilloscopio
fig. 5
fig. 6
Dall’analisi del circuito di fig. 5 risulta che per bassi valori di frequenza del segnale di stimolo Vi il condensatore
presenta una elevata reattanza, di conseguenza la tensione in ingresso Vi la ritroviamo in uscita ai capi del condensatore;
per elevati valori di frequenza il condensatore tende a presentare una bassa reattanza e quindi la tensione Vi si ripartisce
in percentuale maggiore sulla resistenza, quindi, supponendo di non variare la tensione in ingresso durante la prova, la
massima tensione applicabile al circuito non deve superare 50 V.
Per quanto riguarda la frequenza del segnale in ingresso, dall’analisi dei diagrammi teorici di fig. 3 e di fig.4, ci
si accorge che è senz’altro opportuno eseguire le misure sia all’interno della decade che contiene la frequenza di taglio
(100 Hz, 1 kHz) sia nelle decadi attigue (10 Hz, 100 Hz) e (1 kHz, 10 kHz); tale scelta garantisce la possibilità di
tracciare una caratteristica sperimentale sufficientemente ampia ed indicativa delle proprietà del filtro. Le frequenze di
misura vanno poi opportunamente determinate considerando che, se la scala delle frequenze è logaritmica, per poter
costruire correttamente le curve di risposta, le frequenze di misura devono essere scelte in modo tale da essere
geometricamente equispaziate sulla scala delle ascisse.
Così, ad esempio, se nella decade (1 Hz, 10 Hz) si vogliono 5 punti di misura geometricamente equispaziati,
considerato che log(1) = 0 e log(10) = 1 , è necessario scegliere le frequenze in modo che:
log(f1) = 0
⇒
f1 =
1,000 Hz ;
⇒
f2 =
1,778 Hz ;
log(f2) = 0,25
⇒
f3 =
3,162 Hz ;
log(f3) = 0,50
log(f4) = 0,75
⇒
f4 =
5,623 Hz ;
⇒
f5 = 10,000 Hz ;
Analogamente per le altre decadi.
log(f5) = 1
pag. 4
Si sceglie quindi, per il segnale sinusoidale in ingresso, un generatore di funzioni che renda disponibile una
tensione inferiore a 50 V nonché sia in grado di regolare la frequenza almeno nell’intervallo (0 Hz 10 kHz). La scelta
cade, anche per disponibilità del laboratorio, sul generatore di forme d’onda arbitrarie Agilent 33120 A. Detto
generatore svolge anche la funzione di frequenzimetro, in appendice A sono riportate le specifiche tecniche del
generatore, in particolare alla seconda pagina della appendice sono evidenziate le caratteristiche di precisione del
frequenzimetro.
Per la misura dei valori efficaci della tensione in ingresso e della tensione in uscita nonché del ritardo ∆t del
segnale in uscita rispetto al segnale in ingresso si sceglie un oscilloscopio digitale. La scelta cade, anche per
disponibilità del laboratorio, sull’oscilloscopio digitale Agilent 54600 B (o sul modello Agilent 54603 B) completi di
sonde di tensione 10:1 Agilent 10071 A. In appendice B sono riportate alcune specifiche tecniche, in particolare sono
evidenziate le caratteristiche di precisione sia del sistema verticale (misura della tensione) sia del sistema orizzontale
(misura del tempo). Sono da scegliere le indicazioni di incertezza relative alle misure con doppio cursore perché la
tensione efficace, anche se misurata in modo automatico, prevede l’uso di due cursori.
Si osservi che effettuando misure con il doppio cursore sia di tempo che di tensione, al fine di determinare
l’incertezza di misura è necessario conoscere il “full scale” dello strumento dato dal prodotto tra il guadagno verticale
(espresso in V/div o in s/div, è indispensabile annotarlo durante la prova!) ed il numero massimo di divisioni (10
orizzontali ed 8 verticali).
I dati rilevati sperimentalmente vanno riportati in tabella (si prenda come riferimento la tabella riportata in
appendice C) e successivamente in diagramma opportunamente interpolati.
Incertezza di misura
Per quanto riguarda l’incertezza di misura, resta da determinare quella relativa alle grandezze determinate in
modo indiretto ovvero lo sfasamento ∆ϕ e l’attenuazione A espressa sia in valore assoluto che in dB.
Per quanto riguarda lo sfasamento, essendo determinabile tramite l’espressione: ∆ϕ = ω ⋅ ∆t = 2πf ⋅ ∆t ,
calcoliamo subito l’incertezza relativa di caso peggiore:
(
)
u ∆ϕ = u f + u ∆t , da cui si ottiene l’incertezza assoluta di caso peggiore: U ∆ϕ = ∆ϕ ⋅ u f + u ∆t .
Dalle caratteristiche tecniche allegate risulta che u f è data direttamente (20 ppm), mentre per quanto riguarda
l’incertezza sulla misura del ∆t, questa è data (in valore assoluto) mediante la relazione (Horizontal System – Cursor
Accuracy): U ∆t = 0,01% ∆t + 0,2% FSO + 200 ps, pertanto possiamo scrivere (con il full scale FSO ed il ∆t
espressi in secondi):
−12
u∆t = 0,0001 + 0,002
FSO 200 ⋅ 10
+
∆t
∆t
Va però precisato che, essendo f e ∆t non correlate (le misure sono eseguite con strumenti distinti), gli errori
sulla frequenza e sul ∆t sono chiaramente indipendenti, pertanto è possibile applicare la formula del caso più
pag. 5
probabile (con una significativa riduzione dell’incertezza), determinando quindi l’incertezza standard:
⎛ ∂ (∆ϕ ) ⎞
⎛ ∂ (∆ϕ ) ⎞
⎟⎟ ⋅ U ∆2t , std =
⎟⎟ ⋅ U 2f , std + ⎜⎜
U ∆ϕ , std = ⎜⎜
f
(
t
)
∂
∆
∂
⎠
⎝
⎠
⎝
2
2
dividendo ambi i membri per ∆ϕ si avrà:
(2π∆t )2 ⋅ U 2f , std + (2πf )2 ⋅ U ∆2t , std
u ∆ϕ , std = u 2f , std + u ∆2 t , std
Per quanto detto prima, la distribuzione degli errori sulla misura dello sfasamento sarà approssimativamente
gaussiana, per il Teorema del Limite Centrale, essendo relativa ad una variabile aleatoria funzione di più variabili
aleatorie (almeno quattro), ciascuna con una propria distribuzione (che qui assumeremo uniforme, in mancanza di
informazioni precise del costruttore degli strumenti). Pertanto l’incertezza assoluta standard prima calcolata definisce
con buona approssimazione un intervallo di confidenza con grado di fiducia 68 %, mentre altri intervalli di confidenza
possono essere determinati con le consuete regole.
Per quanto riguarda l’attenuazione, sia in valore assoluto che in dB, considerando che le grandezze da cui
dipende sono misurate dallo stesso strumento e quindi correlate e di conseguenza i corrispondenti errori sono non
indipendenti, si deve in ogni caso determinare l’incertezza di caso peggiore:
A=
Vo
Vi
⇒
A dB = 20 ⋅ log(
u A = uVo + uVi
Vo
)
Vi
⇒
⎛U
U ⎞
U A = A ⋅ (uVo + uVi ) = A ⋅ ⎜⎜ Vo + Vi ⎟⎟
Vi ⎠
⎝ Vo
A dB = 20 ⋅ log(Vo ) − 20 ⋅ log(Vi )
Pertanto l’incertezza assoluta su A (espresso in dB) vale:
UA =
20 UVo
20 UVi
20 ⎛ UVo UVi ⎞
20
∂A
∂A
⎟⎟ =
UVo +
UVi =
⋅ (uVo + uVi ) (dB)
⋅
+
⋅
=
⋅ ⎜⎜
+
ln(10) Vo
ln(10) Vi
ln(10) ⎝ Vo
Vi ⎠ ln(10)
∂Vo
∂Vi
Considerato che l’attenuazione (espressa in dB) assume valori prossimi allo 0 non è opportuno esprimere la sua
incertezza in termini relativi.
In appendice C è riportata la tabella su cui riportare le incertezze di misura.
Approfondimenti
Ritorniamo all’incertezza di caso peggiore sull’attenuazione, calcolata nel caso particolare in cui, oltre ad usare
lo stesso strumento (oscilloscopio) per misurare le due tensioni Vo e Vi, lo adoperiamo anche sulla stessa portata. In
questo caso, con buona approssimazione, possiamo ritenere identici gli errori di guadagno nella misura delle due
tensioni, conseguendo quindi una riduzione sensibile dell’incertezza di caso peggiore nella misura del rapporto A. A tal
fine, riportiamo la dichiarazione d’incertezza per le misure d’ampiezza dell’oscilloscopio (Vertical System – Dual
cursor Accuracy):
UV = 1,9% V + 0,4% FSO = uGV % V + U PV
in cui possiamo ritenere l’1,9% come un’incertezza di guadagno, maggiorante del modulo dell’errore di guadagno sulla
retta di riferimento, per ipotesi indipendente dalla lettura effettuata. Pertanto, come già visto dalla teoria, se effettuiamo
una misura di rapporto, il contributo dell’errore di guadagno si elimina e rimane solo il contributo degli altri tipi
d’errore:
⎛ 1
1 ⎞
U A = A ⋅ U PV ⎜⎜
+
⎟⎟
⎝ Vo Vi ⎠
Ovviamente, quanto detto si estende anche al caso dell’espressione di A in dB:
UA =
⎛ 1
20
20
1 ⎞
⋅ (uVo + uVi ) =
⋅U PV ⎜⎜
+
⎟⎟
ln(10)
ln(10)
⎝ Vo Vi ⎠
( dB )
pag. 6
Appendice A
pag. 7
pag. 8
Appendice B
pag. 9
pag. 10
pag. 11
Appendice C
Dati rilevati
n.
f (Hz)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Vi (V)
Kt
KVo
A
A
KVi
∆ϕ
∆t (s)
VO (V)
(V/div.)
(s/div.)
(V/div.) (p.u.) (dB) (rad)
1
2
3
6
10
18
32
56
100
180
320
560
1 000
1 800
3 200
5 600
10 000
Incertezze di misura
n.
uf (%)
uVi (%)
uVo (%)
u∆t (%)
uA (%) UA (p.u.) UA (dB) U∆ϕ (rad) U∆ϕ,std (rad)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
pag. 12












