ESERCITAZIONE N°13
CATENE DI MARKOV
Processo stocastico
I processi stocastici rappresentano l’ampliamento dello studio del calcolo delle probabilità, in quanto,
per la prima volta, è introdotto il concetto di variabile aleatoria collegata al tempo. La definizione di
processo stocastico è la seguente:
"Un processo stocastico è una famiglia di variabili casuali che dipendono da un parametro t".
Un processo stocastico è indicato con la notazione:
dove t è un parametro e T è l’insieme dei possibili valori di t. Di solito con t s'indica il tempo, quindi un
processo stocastico è una famiglia di variabili casuali dipendenti dal tempo. Il campo di variabilità di t,
cioè l’insieme T, può essere un insieme di numeri reali, coincidente, eventualmente, con l’intero asse
dei tempi; può essere anche un insieme discreto di valori. Le variabili casuali Xt sono definite
sull’insieme X, detto spazio degli stati, che può essere un insieme continuo, e in tale caso si parla di
processo stocastico continuo, oppure un insieme discreto, e in tale caso si parla di processo stocastico
discreto. Gli elementi xi X , ossia i valori che possono assumere le variabili casuali Xt, sono detti
stati del sistema e rappresentano i possibili risultati di un esperimento. Le variabili Xt di uno stesso
fenomeno sono legate tra loro da relazioni di dipendenza. Una variabile aleatoria è nota se sono noti
non solo i valori che può assumere, ma anche la distribuzione di probabilità, così per conoscere un
processo stocastico occorre non solo conoscere i valori che possono assumere le Xt, ma anche le
distribuzioni di probabilità delle variabili e le distribuzioni congiunte tra esse. Si possono considerare
anche processi stocastici più semplici in cui il campo di variabilità di t è un insieme discreto di valori
del tempo. Esistono nella realtà numerosi fenomeni che sono studiati mediante la teoria dei processi
stocastici.
Catene di Markov
Un tipo particolare di processi stocastici è costituito dai processi di Markov (che prendono il nome da
A.A. Markov, matematico russo, 1856-1922), definiti come processi nei quali: "il futuro, dato il
presente, è indipendente dal passato". Un processo di Markov è uno studio generalizzato del problema
delle prove ripetute che utilizza il calcolo matriciale, e nel quale il tempo assume un’importanza
fondamentale. Riprendiamo il concetto generale di processo stocastico, come una famiglia di variabili
casuali:
definita sullo spazio X comprendente tutti i possibili valori che le variabili casuali possono assumere.
Come si è detto, lo spazio X è definito spazio degli stati del processo e i suoi elementi xi X , chiamati
stati del sistema, rappresentano i possibili risultati di un esperimento. Un processo stocastico è detto
markoviano se le probabilità di transizione (ossia le probabilità che regolano il passaggio da uno stato
ad un altro stato) dipendono unicamente dallo stato assunto dal sistema nell’istante precedente a quello
considerato. In altre parole, lo stato presente del sistema permette di conoscere il suo comportamento
futuro e la storia precedente non ha influenza; per questo motivo i processi markoviani sono detti
"senza memoria". Tra i vari tipi di processi markoviani, emergono le catene di Markov finite, che sono
processi nei quali il parametro tempo t è discreto e lo spazio degli stati è discreto e finito:
ossia le variabili Xt possono assumere queste n determinazioni.
In altre parole, la probabilità di passare dallo stato xi al tempo k, allo stato xj al tempo k+1, non
dipende dalla storia precedente del sistema, ma è determinata solo dallo stato presente xi. Le probabilità
di transizione, indicate con pij, sono le probabilità condizionate che il sistema passi dallo stato xi al
tempo k, allo stato xj al tempo k+1:
Se le probabilità sono stazionarie (o costanti) nel senso che dipendono dagli stati xi e xj e non
dall’istante k in cui avviene la transizione, la catena di Markov è detta omogenea nel tempo.
Matrice di transizione e vettore iniziale
Se si conoscono le probabilità pij per ogni valore di i e di j, il processo è completamente definito se si
conosce anche la distribuzione di probabilità iniziale, rappresentata da un vettore chiamato vettore
iniziale:
in cui gli elementi q1,0 q2,0 … qn,0 sono le probabilità che il sistema si trovi al tempo zero, negli stati
x1,x2,…xn:
Le probabilità di transizione pij possono essere rappresentate in una matrice P, detta matrice di
transizione:
La matrice P è definita anche matrice stocastica e gode di alcune proprietà:
1a: È quadrata.
2a: Ogni valore di pij è compreso fra zero e uno
3a: La somma degli elementi di ogni riga è uguale a uno. Se anche la somma degli elementi di ogni
colonna è uguale a uno, allora la matrice è detta doppiamente stocastica.
La i-esima riga della matrice di transizione P:
è detta vettore di probabilità e rappresenta la probabilità di tutte le possibili transizioni dello stato xi in
un altro stato in un generico istante.
Evoluzione del vettore di stato iniziale: Vettore di punto fisso
Nota la distribuzione di probabilità iniziale, rappresentata dal vettore V0 e nota la matrice di transizione
P, si può studiare l’evoluzione del vettore di stato moltiplicando, secondo le regole del calcolo
matriciale, il vettore iniziale per la matrice di transizione. Praticamente si riesce a stabilire la
distribuzione di probabilità del vettore quando il sistema compie un passo,. Dati:
sarà:
Nel caso semplificato dei processi di Markov omogenei, nei quali la dipendenza dal tempo sparisce,
l’evoluzione del sistema dopo due passi, dopo tre passi, e in generale dopo n passi è data da:
Un generico elemento pij della matrice di transizione P rappresenta la probabilità che il sistema passi
dallo stato xi allo stato xj in un solo passo. È interessante considerare anche le probabilità in n passi,
indicate con:
che rappresentano le probabilità di transizione dallo stato xi allo stato xj in n passi, con n maggiore di
uno.
Considerando l’evoluzione del vettore di stato, possiamo osservare che:
Pn rappresenta l’ennesima potenza della matrice di transizione P e i suoi elementi sono le probabilità di
transizione pij(n). Se vogliamo determinare la matrice di transizione dopo due passi:
occorre moltiplicare la matrice per se stessa secondo le regole del calcolo matriciale effettuando il
prodotto riga per colonna. Come esempio consideriamo un sistema a tre stati, definito dalla matrice di
transizione a un passo:
Per determinare la matrice a due passi effettueremo il prodotto:
in cui, ad esempio, p112=p11p11 + p12p21 + p13p31
Una catena di Markov si definisce ergodica se e solo se per ogni istante iniziale t0 e per ogni
condizione iniziale di probabilità Vo esiste ed è indipendente da t0 e da Vo, il limite della probabilità
per tempi infiniti :
lim Vo P n T
n
Nella quale T è definito vettore di punto fisso. Le componenti di tale vettore sono le probabilità che il
sistema si trovi nel generico stato all’infinito. T risulta essere un’autovettore per la matrice di
transizione P, infatti:
T P T
ESEMPIO A
Essendo nota la seguente matrice di transizione relativa ad una catena di Markov a stati discreti e finiti:
P
0,30
0,70
0,00
0,60
0,40
0,00
0,20
0,80
0,00
Il cui diagramma di stato associato è il seguente:
Si intende determinare il vettore T di punto fisso tale che:
T P T
Inizialmente fissiamo il vettore iniziale di probabilità Vo, supponendo che all’istante iniziale il sistema
si trovi nello stato 3 (probabilità pari al 100%) :
Vo 0 , 0 , 1
Nota la distribuzione di probabilità iniziale, rappresentata dal vettore V0 e nota la matrice di transizione
P, si può studiare l’evoluzione del vettore di stato moltiplicando, secondo le regole del calcolo
matriciale, il vettore iniziale per la matrice di transizione. In accordo con la seguente relazione:
lim Vo P n T
n
Per ricavare il vettore di punto fisso è necessario eseguire tale prodotto all’infinito, in realtà il processo
in questo caso si arresta velocemente, per cui il vettore di punto fisso è facilmente individuabile.
ITERAZIONI
V
0
0,00 0,00 1,00
1
0,20 0,80 0,00
2
0,54 0,46 0,00
3
0,44 0,56 0,00
4
0,47 0,53 0,00
5
0,46 0,54 0,00
6
0,46 0,54 0,00
7
0,46 0,54 0,00
8
0,46 0,54 0,00
9
0,46 0,54 0,00
10
0,46 0,54 0,00
Il vettore di punto fisso risulta essere:
T 0,46 ; 0,54 ; 0
Per avere conferma della correttezza del vettore di punto fisso appena calcolato, ripetiamo il calcolo
partendo, da un vettore iniziale differente, supponendo, questa volta, che all’istante iniziale il sistema si
trovi nello stato 1 (probabilità pari al 100%) :
Vo 1 , 0 , 0
Procedendo nuovamente con il prodotto matriciale tra il vettore Vo e la matrice di transizione P, si
ottengono i seguenti risultati:
ITERAZIONI
V
0
1,00 0,00 0,00
1
0,30 0,70 0,00
2
0,51 0,49 0,00
3
0,45 0,55 0,00
4
0,47 0,53 0,00
5
0,46 0,54 0,00
6
0,46 0,54 0,00
7
0,46 0,54 0,00
8
0,46 0,54 0,00
9
0,46 0,54 0,00
10
0,46 0,54 0,00
A riprova della correttezza dei calcoli eseguiti durante, si ottiene il medesimo vettore di punto fisso
ricavato in precedenza:
T 0,46 ; 0,54 ; 0
ESEMPIO B
Un guidatore ha le seguenti abitudini. Se prende la strada A il giorno successivo ha probabilità pari a
0,2 di cambiare strada. Se invece prende la strada B ha probabilità pari a 0,7 di cambiare strada il
giorno successivo. A lungo andare quale è la probabilità di prendere una delle due strade?
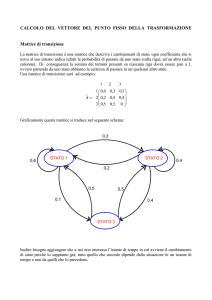
Come prima operazione ricaviamo la matrice di transizione P relativa al sistema in esame:
P
0,80
0,2
0,7
0,3
Il cui diagramma di stato associato è il seguente:
Si intende determinare il vettore T di punto fisso tale che:
T P T
Inizialmente fissiamo il vettore iniziale di probabilità Vo, supponendo che all’istante iniziale il sistema
si trovi nello stato 1, ossia che il guidatore si trovi a percorrere la strada A (probabilità pari al 100%) :
Vo 1 , 0
Nota la distribuzione di probabilità iniziale, rappresentata dal vettore V0 e nota la matrice di transizione
P, si può studiare l’evoluzione del vettore di stato moltiplicando, secondo le regole del calcolo
matriciale, il vettore iniziale per la matrice di transizione. In accordo con la seguente relazione:
lim Vo P n T
n
Per ricavare il vettore di punto fisso è necessario eseguire tale prodotto all’infinito, in realtà il processo
in questo caso si arresta velocemente, per cui il vettore di punto fisso è facilmente individuabile.
ITERAZIONI
0
1
2
3
4
5
6
7
8
9
10
Il vettore di punto fisso risulta essere:
T 0,78 ; 0,22
V
1
0,8
0,78
0,778
0,7778
0,77778
0,777778
0,777778
0,777778
0,777778
0,777778
0
0,2
0,22
0,222
0,2222
0,22222
0,222222
0,222222
0,222222
0,222222
0,222222
Per avere conferma della correttezza del vettore di punto fisso appena calcolato, ripetiamo il calcolo
partendo, da un vettore iniziale differente:
Vo 0,3 ; 0,7
Procedendo nuovamente con il prodotto matriciale tra il vettore Vo e la matrice di transizione P, si
ottengono i seguenti risultati:
ITERAZIONI
0
1
2
3
4
5
6
7
8
9
10
V
0,3
0,73
0,773
0,7773
0,77773
0,777773
0,777777
0,777778
0,777778
0,777778
0,777778
0,7
0,27
0,227
0,2227
0,22227
0,222227
0,222223
0,222222
0,222222
0,222222
0,222222
A riprova della correttezza dei calcoli eseguiti durante, si ottiene il medesimo vettore di punto fisso
ricavato in precedenza:
T 0,78 ; 0,22