CALCOLO DEL VETTORE DEL PUNTO FISSO DELLA TRASFORMAZIONE
Matrice di transizione
La matrice di transizione è una matrice che descrive i cambiamenti di stato; ogni coefficiente che si
trova al suo interno indica infatti la probabilità di passare da uno stato (sulla riga), ad un altro (sulla
colonna). Di conseguenza la somma dei termini presenti su ciascuna riga dovrà essere pari a 1,
ovvero partendo da uno stato abbiamo la certezza di passare in un qualsiasi altro stato.
Una matrice di transizione sarà ad esempio:
1
2
3
1 0,6 0,3 0,1
A 2 0,2 0,4 0,4
3 0,5 0,5 0
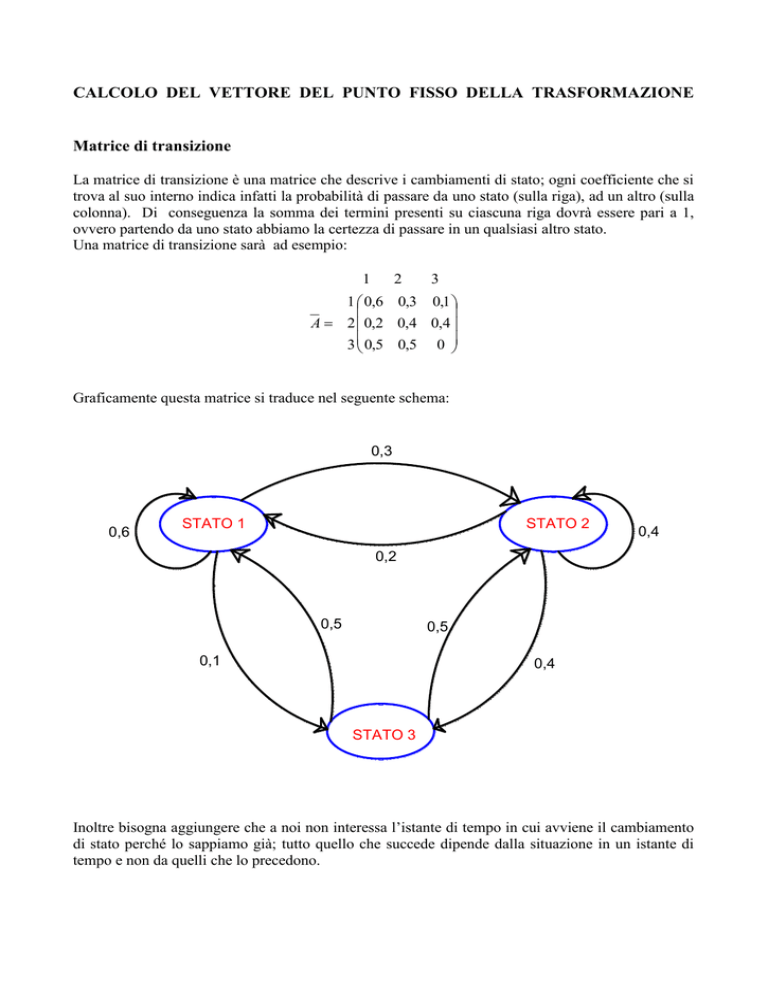
Graficamente questa matrice si traduce nel seguente schema:
0,3
0,6
STATO 1
STATO 2
0,4
0,2
0,5
0,5
0,1
0,4
STATO 3
Inoltre bisogna aggiungere che a noi non interessa l’istante di tempo in cui avviene il cambiamento
di stato perché lo sappiamo già; tutto quello che succede dipende dalla situazione in un istante di
tempo e non da quelli che lo precedono.
Vettore del punto fisso della trasformazione
Possiamo scrivere dei vettori riga ti che assumono la seguente forma:
t i (a11
a12
a13 )
In questo caso abbiamo tre coefficienti perché abbiamo esaminato 3 stati; a11 rappresenta la
probabilità di trovarsi nello stato 1, a12 rappresenta la probabilità di trovarsi nello stato 2 e a13
rappresenta la probabilità di trovarsi nello stato 3.
Così ad esempio il vettore:
t i (1 0 0)
rappresenta la certezza di trovarsi nello stato 1, mentre il vettore:
t i (0,5 0,5 0)
rappresenta la probabilità del 50% di trovarsi nello stato 1 e del 50% di trovarsi nello stato 2.
Se ora partiamo con un vettore qualsiasi che mi descrive la situazione all’istante zero come ad
esempio:
t 0 (1 0 0)
e lo moltiplichiamo per la matrice di transizione A, otteniamo un vettore t1 che mi descrive le
probabilità di trovarsi nei vari stati all’istante 1:
t 0 A t1
0,6 0,3 0,1
1 0 0 0,2 0,4 0,4 0,6 0,3 0,1
0,5 0,5 0
Quindi se vogliamo conoscere la situazione all’istante 2, basterà moltiplicare il vettore che descrive
l’istante 1 per la matrice di transizione:
t 2 t1 A t 0 A A
Risulta così logico, generalizzando, che se vogliamo conoscere la situazione all’istante n-esimo,
basterà moltiplicare il vettore iniziale che descrive l’istante 0 per la matrice di transizione elevata a n:
tn t0 A
n
Se ora faccio il limite per n tendente all’infinito del prodotto tra il vettore che descrive l’istante 0
per la matrice di transizione elevata a n ottengo un vettore T chiamato vettore del punto fisso della
trasformazione:
lim
t 0 A n T
n
Quindi se le trasformazioni vanno all’infinito, o comunque dopo un determinato numero, le
probabilità di trovarsi nello stato 1, 2 o 3 sono rappresentate dalle componenti del vettore T .
Logicamente sarà utile utilizzare un foglio di calcolo di tipo Excel per effettuare questi prodotti, in
modo da osservare quando le componenti del vettore risultante si stabilizzano e quindi si ripetono
nonostante la matrice di transizione venga ulteriormente moltiplicata con il vettore rappresentante
l’istante precedente; solo allora potremo dire che quel vettore rappresenta il vettore del punto fisso
della trasformazione.
Non sempre esiste il vettore del punto fisso della trasformazione; quando esiste la matrice di
transizione si dice regolare.












