DIREZIONE DIDATTICA “ALBERT SABIN ”
C.so Vercelli 157 – 10155 Torino
PROGRAMMAZIONE DI ISTITUTO QUARTA
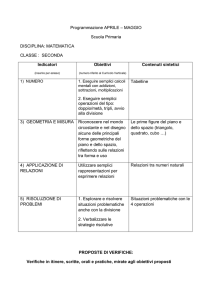
DISCIPLINA: MATEMATICA
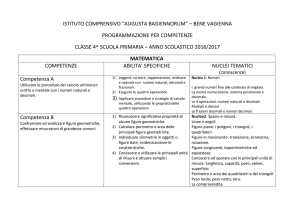
COMPETENZE
LOGICA classi 4^ e 5^
INTRODUZIONE AL
PENSIERO
RAZIONALE:
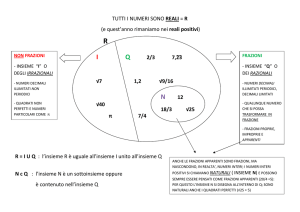
* INSIEMI
* RELAZIONI
1. LINGUAGGIO
1. Classificare oggetti, figure,
numeri in base a due o più
attributi e viceversa, dati due o
più attributi spiegare la
classificazione data
CONTENUTI
METODOLOGIE
1.a) attività di classificazione, sia
in ambito matematico sia nelle
altre discipline
1.b) approfondimento e
consolidamento di concetti di
insieme, elemento, appartenenza,
non appartenenza,complementare,
insiemi disgiunti, congiunti,
sottoinsiemi e inclusione
1.c) relazioni tra elementi dello
stesso insieme e di insiemi diversi
ed individuare le proprietà
(riflessiva,simmetrica, transitiva)
1.d) realizzazioni adeguate di
rappresentazioni delle
classificazioni mediante
diagrammi di Venn, di Carrol, ad
albero, con tabelle
1.e) lettura,comprensione ed
interpretazione di
rappresentazioni date
Il nostro percorso per
apprendere/insegnare matematica non si
basa su un’unica metodologia scelta
perché più efficace o moderna di altre, ma
tiene conto degli stimoli, delle indicazioni,
degli aspetti positivi che possiamo
cogliere in diversi approcci metodologici
conosciuti in questi anni e sperimentati nel
nostro lavoro con le classi.
Proviamo ad elencare le metodologie che
fanno da sfondo al nostro lavoro o che
sono comuni a più insegnati della scuola:
-insiemistica: utile perché usa e rafforza la
logica, perché parte delle esperienze
concrete/pratiche, offre un modello di
rappresentazioni iconiche che progredisce
con le scoperte e conoscenza fino alla
simbolizzazione e all’estrazione.
- metodo sperimentale o di ricerca:
comune a tutte le scienze e quindi anche
alla matematica , consente di partire da
situazioni reali o simulate, permette ai
bambini di fare osservazioni, ipotizzare
cambiamenti e nuove esperienze da
verificare insieme per scoprire nuovi
concetti e nuove tecniche.
- metodologia attiva: ha come centro il
bambino che fa esperienze, opera in
situazioni pratico operative per scoprire il
suo “sapere” attraverso il suo “saper fare”.
MEZZI
STRUMENTI
VERIFICHE
VALUTAZIONI
Entrambi i plessi della scuola hanno un
laboratorio di matematica abbastanza
fornito di materiali e strumenti utili
nell’attività nell’area matematica.
Alcuni strumenti sono richiesti come
materiali individuale fornito dalle famiglie
in quanto si prestano ad un uso e consumo
individuale.
In tutte le classi si usano libri di testo ed
esercitazioni specifici per la matematica,
sono richiesti fogli o quaderni a quadretti
0,5 cm., quadblock con quadretti da 1 cm.
Si inizia a lavorare in 1° con materiale non
strutturato ed infine a strumenti veri e
propri sempre più specifici.
Elenchiamo alcuni materiali e strumenti,
più usati nelle classi, suddivisi per settori
dell’area matematica:
Logica: blocchi logici, tappeti logici,
schemi come diagrammi, istogrammi e
tabelle.
Numeri operazioni: materiale non
strutturato, mani, numeri in colore, abaci,
materiale multibase con diverse basi e a
base 10, bilance aritmetiche e confezioni
di 0 + 1 o pascaline.
Geometria: blocchi logici, confezioni di
figure geometriche piane e solide,
geopiani, compassi.
Misura: righelli e righe, metri, metro a
ruota, squadre ( 90°, 45° 45° e 90°, 60° e
30° )
Riteniamo che qualsiasi verifica proposta
ai nostri allievi per valutare ciò che sanno
“gli esiti” serva anche e soprattutto come
elemento importante del processo di
autovalutazione perché ci aiuta a capire
dove c’è qualcosa di sbagliato da
modificare; gli errori dei bambini possono
diventare una risorsa se diventano
qualcosa sul quale lavoriamo per capire
percorsi e strategie, per modificare
linguaggi e metodologie, per
riprogrammare il nostro lavoro e quello
delle classi e renderlo più efficace.
Tale premessa per dire che la
programmazione non è lineare, ma
circolare, dopo le verifiche e le valutazioni
si ricomincia mettendo in atto opportune
scelte su obiettivi, contenuti, metodologie
e strumenti.
L’autovalutazione è più significativa
quando diventa un processo condiviso da
tutti gli insegnanti di classe, d’interclasse
e di scuola.
A tale proposito è già da alcuni anni, che
nella nostra scuola facciamo verifiche
comuni d’ingresso, al 1° q., al 2° q.
suddivisi per ambiti disciplinari.
Oltre a tali verifiche ufficiali in tutte le
classi si fanno verifiche in itinere alla fine
di ogni unità, a volte alcune esercitazioni
possono assumere importanza per la
valutazione perché ci fanno cogliere un
ostacolo di apprendimento o la conferma
di un’acquisizione raggiunta da tutti.
COMPETENZE
CONTENUTI
METODOLOGIE
1.f) analisi e confronto elle varie
-cooperative learning: il bambino è
inserito in un contesto sociale di pari
indispensabile per lo sviluppo delle
relazioni sociali, ma anche per lo sviluppo
del suo apprendimento che viene facilitato
e stimolato dallo scambio e dal lavoro in
coppia e in gruppo.
L’insegnamento in tale metodologia
assume ruoli interessanti come
organizzatore, facilitatore, supervisore.
metodo basato sull’errore come risorsa:
soprattutto in matematica considerata dai
bambini come scienza esatta, nella quale o
si fa giusto o si sbaglia è necessario come
insegnanti impostare con la classe un
lavoro che aiuti a capire le strategie
utilizzate, quali portano all’errore e
perché; attraverso la “discussione
matematica” guidata a confronto
esecuzioni diverse per scoprire dove,
perché, in che modo sbaglia, ma
soprattutto innescare strategie di
autocontrollo dei risultati.
Anche le modalità organizzative delle
lezioni di matematica sono diversificate:
- ci sono momenti di introduzione ai
concetti ed argomenti nuovi, hanno
carattere collettivo, usano spesso il
“braimstorming” per raccogliere le
informazioni che i bambini possiedono.
- ci sono proposte di attività collettive
concrete con o senza materiale.
- ci sono spiegazioni collettive condotte
dall’insegnante anche utilizzando il libro
di testo.
- ci sono esercitazioni di classe, a gruppo
ed individuale
- ci sono correzioni collettive e/o
individuali delle esercitazioni fatte a
scuola e di compiti scritti assegnati a casa
- ci sono specifiche esercitazioni ed
esecuzioni individuali per le verifiche in
itinere e valutazione.
rappresentazioni evidenziandone
l’equivalenza percettiva e le
diverse caratteristiche
1.g) utilizzo della
rappresentazione più
adeguata e funzionale ad una data
situazione
2. Usare correttamente il
linguaggio degli insiemi nelle
operazioni di unione e
intersezione,anche in relazione
alle classificazioni aritmetiche,
geometriche,scientifiche,
grammaticali
2.a) esecuzione e verbalizzazione
correttamente le operazioni di
Unione, intersezione,
complementazione
2.b) acquisizione di proprietà di
linguaggio e correttezza d’uso dei
connettivi logici e della negazione
nelle operazioni insiemistiche e
nelle classificazioni
2.c) consolidamento della
comprensione e l’uso dei
quantificatori:esercizi di ricerca
del valore di verità
MEZZI
STRUMENTI
Goniometro, bilance per i pesi e
contenitori.
VERIFICHE
VALUTAZIONI
Un ultimo aspetto della valutazione ci
trova concordi: le verifiche ci dicono ciò
che i bambini sanno fare in modo
autonomo ed anche ciò che i bambini
capiscono in modo autonomo della
consegna, ogni verifica è un elemento che
ci dice del bambino in quel momento, in
quel esercizio specifico, la valutazione che
diamo sulla scheda per esprimere il livello
che ogni bambino ha rispetto alla
disciplina è più complessa e non può
quindi dipendere dalle singole prove.
Le prove di verifica concordate a livello di
interclasse coprono tutti i settori della
matematica e sono diversi anche come
modalità di presentazione.
Negli anni abbiamo raccolto tali prove in
un dossier di scuola che può essere
consultato ed utilizzato nei momenti delle
scelte.
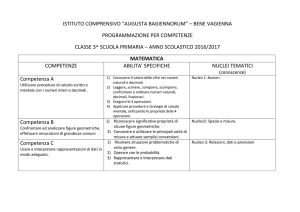
COMPETENZE
PROBABILITA’
STATISTICA
INFORMATICA
1. Compiere osservazioni,
semplici rilevamenti
statistici e tracciare diagrammi
“a barre”,istogrammi
e aerogrammi; leggere
diagrammi dati
2. Calcolare medie aritmetiche e
percentuali e
viceversa, interpretare
rappresentazioni e calcoli
3. Rappresentare, elencare e
numerare tutti i possibili
casi in semplici situazioni
combinatorie; dedurre
alcune elementari valutazioni
di probabilità
CONTENUTI
1.a) raccolta, organizzazione e
rappresentazione dei dati desunti
da una determinata situazione
che si sta analizzando
2.a) ricerca su libri e giornali dati
e rappresentazioni statistiche ed
interpretazione
2.b) calcoloed interpretazione
della media aritmetica di
determinati rilevamenti statistici
3.a) analisi e rappresentazione del
gioco dei dadi, del pari e dispari,
il lancio di monete,l’estrazione di
gettoni, di carte da un mazzo
3.b) individuazione di quanti e
quali numeri si possono formare
con un abaco a tre posizioni,
quante e quali parole si possono
formare con 2 – 3 - …lettere
METODOLOGIE
MEZZI
STRUMENTI
VERIFICHE
VALUTAZIONI
COMPETENZE
4. Confrontare, in situazioni di
gioco, le probabilità
dei vari eventi
5. Tracciare ed interpretare
diagrammi di flusso per la
Rappresentazione di
convenienti processi (percorsi,
azioni, racconti, problemi)
CONTENUTI
4.a) consolidamento delle attività
ed i concetti di possibileimpossibile, certo-incerto, non so,
forse…
4.b) ipotesi di probabilità facendo
ricorso all’esperienza personale e
successivamente, confrontare le
proprie convinzioni con la
probabilità sperimentale e
matematica
5.a utilizzo di diagrammi di
flusso per rappresentare “catene”
di operazioni e la risoluzione di
un problema
5.b) costruzione di codici con cui
rappresentare percorsi mediante
diagrammi di flusso
METODOLOGIE
MEZZI
STRUMENTI
VERIFICHE
VALUTAZIONI
COMPETENZE
ARITMETICA
I NUMERI INTERI
1) Operare nella successione dei
numeri interi entro
Ed oltre il 100.000
CONTENUTI
1.a)riconoscimento, lettura e
scrivere i numeri entro e oltre il
100.000
1.b) numerazione in successione
progressiva e regressiva con i
numeri interi
1.c) relazioni di maggioranza,
minoranza e uguaglianza tra
numeri interi
1.d) individuazione delle regole
in una successione numerica
1.e) ripetizione di tabelline in
sequenze ordinate e non
LE FRAZIONI
2. Approfondire il concetto di
frazione
3. Classificare le frazioni
2.a) rappresentazione di diversi
tipi di frazione
2.b) calcolo della frazione di un
numero
2.c) la frazione complementare
con i regoli e le figure
geometriche
3.a) differenze tra la frazione
propria, impropria, apparente
3.b) conoscenza di altri tipi di
frazione ( decimali, equivalenti)
3.c) confronto e ordine di frazioni
riferendosi a figure
3.d) collocazione delle diverse
frazioni sulla linea dei numeri
METODOLOGIE
MEZZI
STRUMENTI
VERIFICHE
VALUTAZIONI
COMPETENZE
NUMERI DECIMALI
CONTENUTI
4.a) individuazione e
4. Acquisire il concetto di numero registrazione delle frazioni
decimali
decimale
4.b) passaggio dalle frazioni
decimali ai numeri decimali
4.c) conoscenza del valore
posizionale delle cifre in numeri
interi e decimali
4.d) lettura, scrittura,
composizione e scomposizione
dei numeri decimali
4.e ) relazioni di maggioranza,
minoranza e uguaglianza fra
numeri decimali e non
4.f esecuzione, con i numeri
decimali e non numerazioni
progressive e regressive
4.g) collocazione dei numeri
decimali sulla linea dei numeri.
LE OPERAZIONI
5. Padroneggiare abilità di calcolo
orale e scritto con
5.a) addizioni in colonna con
numeri interi
numeri interi
5.b) sottrazioni in colonna con
numeri interi
5.c) moltiplicazioni in colonna
con numeri interi
5.d) divisioni in colonna con
numeri interi con 2 e
3 cifre divisore
5.e) verifica dell’esattezza delle
singole operazioni
5.f) moltiplicazioni e divisioni 10
– 100 – 1000
METODOLOGIE
MEZZI
STRUMENTI
VERIFICHE
VALUTAZIONI
COMPETENZE
CONTENUTI
5.g) calcoli orali
5.h)applicazione delle proprietà
delle 4 operazioni
5.i) conosce i multipli
5.j) conosce i divisori
6. Padroneggia abilità di calcolo
scritto con numeri
decimali
6.a) addizioni in colonna con
numeri decimali
6.b) sottrazioni in colonna con
numeri decimali
6.c) moltiplicazioni in colonna
con numeri decimali
7.a) addizioni, sottrazioni,
7. Padroneggiare abilità di calcolo moltiplicazioni e divisioni con
con numeri misti
numeri interi e decimali
PROBLEMI
SITUAZIONI
PROBLEMATICHE
1. Riconoscere una situazione
problematica, individuare le
informazioni e le richieste
1.a) comprensione del problema
1.b) individua i dati eccedenti
1.c) sa individua dati mancanti
1.d) individua la richiesta del
problema
1.e) quantità numeriche nel testo
di un problema già risolto
1.f) argomenta il ragionamento
scelto o fatto nella risoluzione del
problema.
METODOLOGIE
MEZZI
STRUMENTI
VERIFICHE
VALUTAZIONI
COMPETENZE
2. Risolvere situazioni
problematiche con diverso
Grado di complessità
CONTENUTI
2.a) problemi con due domande e
due operazioni
2.b problemi con una domanda e
due operazioni
2.c) problemi con costo unitario e
costo totale
2.d) sa risolvere problemi con
peso netto, peso lordo, tara
2.e) problemi con le frazioni
2.g) problemi contenenti anche
un’equivalenza
2.h) problemi con due domande e
più operazioni
2.i) rappresenta, tramite
diagrammi, un percorso risolutivo
2.j) formula il testo di un
problema a partire da una
rappresentazione
2.k)formula il testo di un
problema partendo dalla risposta
2.l) approccio ai problemi di
geometria
METODOLOGIE
MEZZI
STRUMENTI
VERIFICHE
VALUTAZIONI
COMPETENZE
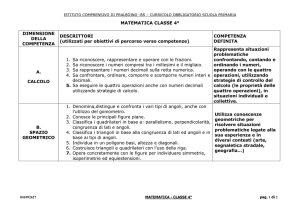
GEOMETRIA
OPERARE CON
FIGURE,
GRANDEZZE E
MISURE
1. Riconoscere gli elementi
fondamentali della
geometria piana
2. Operare trasformazioni di
figure geometriche
piane
3. Classificare poligoni
4. Acquisire il concetto di
perimetro
CONTENUTI
1.a) riconosce l’angolo come
parte di piano e come rotazione
1.b) classificazioni e misurazioni
dei vari tipi di angolo
1.c) classificazioni di poligoni in
base al numero dei vertici e al
numero e al tipo di lati e angoli
2.a) consolidamento i concetti di
simmetria ed equivalenza tra
figure
2.b) relazioni spaziali di
congruenza
3.a) diversi tipi di quadrilateri
3.b) classifica i triangoli
3.c) vari tipi di poligoni regolari
e non
4.a) calcolo del perimetro di
triangoli e quadrilateri
4.b) formula diretta per calcolare
rapidamente il perimetro
4.c)uso le formule inverse
5. Acquisire concetto di area
5.a) confronto le figure
5.b) le figure complesse
5.c) calcolo dell’area di triangoli
e quadrilateri
METODOLOGIE
MEZZI
STRUMENTI
VERIFICHE
VALUTAZIONI
COMPETENZE
CONTENUTI
5.d) calcolo la dimensione
incognita di triangoli e
quadrilateri
5.e) utilizzo delle formule
inverse
6. Avviare all’attività di misura
attraverso stime ed
uso di campioni in situazioni
operative e pratiche.
6.a) misura lunghezze con unità
arbitrarie
6.b) acquisizione dell’idea di
misura come numero
6.c) sceglie il campione più adatto
6.d) riconoscimento l’equivalenza
tra una lunghezza espressa con un
certo campione e la stessa
espressa con un altro campione
6.e) valutazione di capacità con
un confronto diretto
6.f) utilizzo campioni di misura
arbitrari
6.g) ordine di recipienti secondo
la capacità
6.h) confronto tra oggetti con
l’uso della bilancia
6.i) ordine degli oggetti secondo
il loro peso
7. Passare dall’uso di campioni 7.a) primo approccio alle unità di
arbitrari a quello delle misure
convenzionali
lunghezza ,peso e capacità
convenzionali
7.b) primo approccio al concetto
di equivalenza utilizzando
le misure di lunghezza
METODOLOGIE
MEZZI
STRUMENTI
VERIFICHE
VALUTAZIONI