MISURE MECCANICHE E TERMICHE
A.A. 2012-2013
Lezione n.7 (25.10 2012)
PROPRIETÀ METROLOGICHE DEGLI STRUMENTI
PRECISIONE - METODO A POSTERIORI
Il metodo a posteriori (o a scatola chiusa) prescinde dal funzionamento dello strumento; consiste
nell’esecuzione di un numero opportuno n di misure (x1, x2,….. xi,…… xn), e nella elaborazione
statistica delle misure stesse. Le misure devono essere eseguite sempre con lo stesso strumento,
nelle stesse condizioni e sulla stessa grandezza.
Il metodo serve prevalentemente all’utilizzatore che deve sapere da che errore è affetta la misura
della grandezza rilevata.
In questo caso, nella:
x xo x ,
per il valore più probabile xo, viene assunto il valor medio delle n misure:
xo = x xi / n ,
mentre per il calcolo dell’errore εx = Δx, occorrono considerazioni più complesse.
Si osservi che il valor medio è una “stima” del valor vero x* che non potrà mai essere determinato
esattamente in quanto ottenuto mediante una misurazione che è un procedimento sperimentale.
Si ricorda anzitutto che si definisce probabilità di un evento il rapporto (calcolabile a priori) fra casi
favorevoli e casi possibili, mentre si definisce frequenza di un evento il rapporto (calcolabile a
posteriori) fra numero di volte in cui un evento si presenta e numero totale di eventi.
E’ un fatto sperimentale che, all’aumentare del numero di prove, la frequenza di un evento tende
alla sua probabilità (legge empirica del caso).
Si consideri ora lo scarto della singola misura:
i xi x ,
e si consideri il numero n i di scarti che cadono in un intervallo di ampiezza , o la loro frequenza
i ni / n ; dovrà naturalmente risultare
=1.
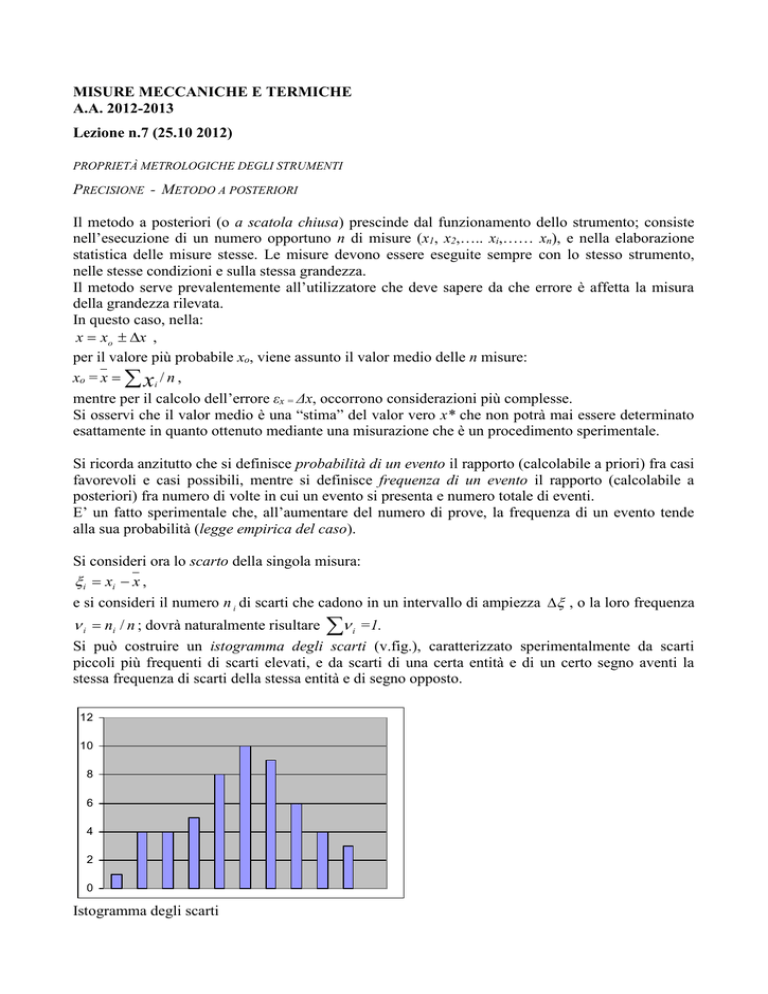
Si può costruire un istogramma degli scarti (v.fig.), caratterizzato sperimentalmente da scarti
piccoli più frequenti di scarti elevati, e da scarti di una certa entità e di un certo segno aventi la
stessa frequenza di scarti della stessa entità e di segno opposto.
12
10
8
6
4
2
0
Istogramma degli scarti
i
Se il numero di misure è molto elevato ( n ), l’ampiezza diventa infinitesima ( d );
in tal caso si può sostituire l’istogramma delle frequenze degli scarti con la curva di distribuzione
delle frequenze degli scarti.
Tale curva deve avere il massimo nell’origine, tendere a zero per , e deve essere una curva
pari.
Si può quindi far riferimento a una curva di Gauss (o curva a campana), del tipo:
2
f ( ) e ;
in tal caso però non si tiene conto del fatto che ha le dimensioni della grandezza da misurare e che
l’area sottesa alla curva è 1. Si introduce pertanto un parametro h, detto modulo di precisione e si
scrive:
2 2
he h
;
f ( )
il modulo di precisione ha le dimensioni dell’inverso dello scarto (e quindi della grandezza
misurata); la frequenza degli scarti in un intervallo generico [1,2] è allora data da:
2 2
2
2
he h
= f ( )d =
d .
1
1
Si supponga ora di eseguire la n+1esima misura; con riferimento alla legge empirica del caso tale è
anche la probabilità (calcolata quindi a priori) di trovare uno scarto nello stesso intervallo.
In altre parole:
2 2
2
he h
P1,2 =
d .
1
Allo stesso modo, la probabilità che la n +1 esima misura cada nell’intervallo x1 , x2 è data da:
P x1 , x2 =
x2
x1
he h
2
( x x)
2
dx
Sono stati fin qui considerati gli scarti delle misure, che sono noti in quanto dati dalla differenza fra
singola misura e valor medio delle n misure effettuate:
i xi x .
Si considerino ora gli errori, che sono dati dalla differenza fra singola misura e valor vero x*
incognito (e comunque, come detto, non determinabile in modo esatto); l’errore della singola
misura:
i xi x * ,
risulta pertanto incognito; si osservi però che, anche se tale errore è incognito, la differenza tra
errore e scarto di una misura è una quantità costante:
i i x x* ;
: errore della media.
Segue che la curva di distribuzione degli errori può considerarsi traslata di rispetto a quella di
distribuzione degli scarti; la curva di distribuzione degli errori, è pertanto “centrata” attorno al valor
vero così come quella di distribuzione degli scarti è centrata attorno al valor medio; la probabilità
che un errore cada in un intervallo [1, 2], è data da:
2 2
2
2
he h
P = f ( )d =
d .
1
1
Per determinare il modulo di precisione h, si faccia ora riferimento all’errore quadratico medio detto
anche scarto tipo o, più generalmente, deviazione standard:
2
i
/n .
Non conosciamo i singoli errori i, ma possiamo ricordare i i ; gli scarti delle singole
misure sono noti; ponendo allora per l’errore della media:
/ n (v. oltre: Propagazione degli errori),
si dimostra facilmente che:
i2 /( n 1) =
( xi x) 2
.
n 1
Pertanto la deviazione standard può essere calcolata a partire dagli scarti ed è quindi una quantità
nota. Poiché, per definizione, in base alla curva di distribuzione degli errori,
2 2
2
1
2 he h
2
2
,
i / n = f ( )d =
d =
1
h 2
1
si trova per h (integrando per parti), il valore:
1
.
h
2
E’ quindi noto il modulo di precisione, ed è quindi nota la curva di distribuzione degli errori e, di
conseguenza, è nota la probabilità che un errore cada in un certo intervallo [1, 2].
Come già accennato, la media x è una stima del valor vero x. In figura sono riportate alcune
curve di distribuzione delle misure, in cui la media x è indicata con :
x 2
2 .
e
f(x) =
2
2
1
Si osservi che all’aumentare di la curva si appiattisce; infatti elevato significa modulo di
precisione h non elevato (e viceversa).
Si può dimostrare che la curva di distribuzione degli errori ha due punti di flesso per:
,
ovvero che la curva di distribuzione delle misure ha due punti di flesso per:
x – x = x - x* = .
Calcolando le aree sottese a intervalli di errore diversi, si dimostra che la probabilità di avere un
errore nell’intervallo:
è pari a 0,68 ;
1,96 è pari a 0,95 ;
è pari a 0,997.
3
Tali sono anche le probabilità che una misura x differisca da , stima di x* di una quantità compresa
negli stessi intervalli.
Si osservi che finora si è fatto riferimento alla distribuzione delle singole misure e alla distribuzione
dei relativi errori. Per quanto riguarda la media x , valore più probabile della grandezza misurata, si
può ragionare come segue:
si supponga di eseguire più serie di misure, p, e di calcolare le medie:
x1 , x 2 , ...... x j , ...... x p .
E’ ragionevole ipotizzare che la media delle medie:
x xj / p
tenda a x*, e che le medie siano distribuite secondo una curva di Gauss (distribuzione normale)
attorno a x .
Occorrerebbe ripetere per le medie x j il procedimento adottato per le singole misure xi e calcolare
l’errore quadratico medio delle medie o deviazione standard delle medie x .
Si può però dimostrare che x si può trovare a partire da una sola di misure (vedi ancora: Principio
di propagazione degli errori), e, più precisamente che :
x= / n= .
Ripetendo il ragionamento precedente, si dimostra allora che la probabilità che una media x
(quindi, in particolare la media delle n misure assunta come valore più probabile della grandezza),
differisca dalla media delle medie x della popolazione (assunta come valor vero x*), di una
quantità compresa nell’intervallo:
è pari a 0,68 ;
x
1,96 x è pari a 0,95 ;
è pari a 0,997.
3x
In altre parole la probabilità che il valor vero x* incognito di una grandezza cada fuori
dall’intervallo:
è pari a 0,32 ;
x x
x 1,96 x è pari a 0,05 ;
x 3 x è pari a 0,003.
Per tale ragione l’intervallo 3 x può essere assunto come indice della precisione della misura
adottata, vista la probabilità estremamente piccola che x* cada fuori da tale intervallo.
N.B.
La posizione fatta per l’errore della media , ovvero per la deviazione standard delle medie :
x = / n = ,
potrebbe far pensare che con un numero molto elevato di misure l’errore della media potrebbe
annullarsi; in realtà n può essere elevato ma non elevatissimo, perché non è possibile rilevare
indefinitamente la stessa grandezza con lo stesso strumento sempre nelle stesse condizioni.
ESEMPIO DI APPLICAZIONE DEL METODO A POSTERIORI
Si supponga di aver eseguito 36 misurazioni del diametro di un tondo e di aver trovato,
un diametro medio pari a :
D 40mm ,
E una deviazione standard pari a :
D 0,6mm .
In tal caso, la probabilità che eseguendo la trentasettesima misura si trovi un valore compreso tra
39,4 e 40,6 mm ( D ) è del 68 %, mentre la probabilità di trovare un valore inferiore a 38,8 mm
( 2 D ) è pari a 2,5 %.
Se si vuole invece calcolare la probabilità che il diametro vero (incognito !),, sia compreso in un
certo intervallo, si deve fare riferimento alla deviazione standard della media:
D = D / 36 = 0,1mm ;
pertanto la probabilità che D* sia compreso nell’intervallo 39,8 mm – 40, 2 mm ( 2 D ) è del 95
%, mentre la probabilità che sia D* superiore a 40,1 mm è del 16%.
Infine l’errore da attribuire a D 40mm è pari a + 0,3 mm ( 3 D ).