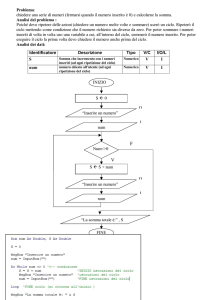
POLITECNICO DI MILANO
Facoltà di Ingegneria Industriale
Corso di Laurea specialistica in
Ingegneria Meccanica
Modello previsionale per la precipitazione di microalliganti
in acciai al niobio e alluminio
Relatore:
Prof. Carlo MAPELLI
Co-relatore:
Ing. Andrea GRUTTADAURIA
Tesi di Laurea di:
Stefano CARDELLINI Matr. 764484
Anno Accademico 2011 - 2012
2
Indice
Indice figure ..........................................................................................................5
Indice tabelle .........................................................................................................9
Sommario ............................................................................................................11
Abstract ...............................................................................................................12
CAPITOLO 1 ......................................................................................................13
Modello sulla precipitazione in acciai HSLA (Particle-Size-Grouping Model) .13
1.1 Introduzione ..............................................................................................13
Heat Transfer Model ...................................................................................19
Equilibrium Precipitation Model.................................................................19
Kinetic Model.............................................................................................20
Esperimento.................................................................................................21
Risultati esperimento ...................................................................................24
1.2 Heat Transfer Model .................................................................................30
Formulazione del modello...........................................................................32
Conduzione del calore nella matrice di acciaio...........................................33
Trasferimento del calore nel gap tra matrice e lingottiera ..........................33
Bilancio di massa e quantità di moto sugli strati di scorie ..........................37
Conduzione del calore nella lingottiera.......................................................39
Convezione dell’acqua di raffreddamento ..................................................41
Zona di raffreddamento secondario (zona ugelli) .......................................43
Soluzione metodologica ..............................................................................45
1.3 Equilibrium Precipitation Model...............................................................48
Prodotti di Solubilità ...................................................................................48
Bilancio di massa ........................................................................................53
Soluzione numerica .....................................................................................55
1.4 Kinetic Model............................................................................................59
Il Modello PSG per “collisione” .................................................................62
Il Modello PSG per “diffusione”.................................................................64
Indice
CAPITOLO 2...................................................................................................... 71
Modello numerico sulla precipitazione di microalliganti in acciai al niobio ..... 71
2.1 Determinazione della temperatura critica di precipitazione ..................... 72
2.2 Variazione delle concentrazioni e coefficiente di diffusione ................... 76
2.3 Fase di nucleazione ................................................................................... 79
2.4 Fase di accrescimento ............................................................................... 83
2.5 Valutazione della densità numerica dei precipitati nel tempo .................. 87
CAPITOLO 3...................................................................................................... 95
Analisi sperimentale e confronto con il modello di simulazione ....................... 95
Analisi dei precipitati mediante FEG-SEM ................................................ 99
CAPITOLO 4.................................................................................................... 131
Risultati e confronti .......................................................................................... 131
4.1 Variazione dell’energia di interfaccia precipitati/matrice ...................... 132
4.2 Variazione percentuale del calore latente di fusione .............................. 133
4.3 Variazione della percentuale nominale di niobio ................................... 134
4.4 Variazione della percentuale nominale di carbonio................................ 137
4.5 Analisi di casi particolari ........................................................................ 139
4.6 Confronto tra diversi precipitati.............................................................. 140
CONCLUSIONI ............................................................................................... 145
APPENDICE .................................................................................................... 149
Bibliografia ....................................................................................................... 167
Ringraziamenti .................................................................................................. 169
4
Indice figure
Figura 1.1. Un esempio di processo di saldatura. ...............................................14
Figura 1.2. L'incendio di un grattacielo ad Astana, Kazakhistan. .......................15
Figura 1.3. Un esempio di serbatoio sotterraneo per lo stoccaggio di gas naturale
liquefatto. ............................................................................................................16
Figura 1.4. Treno per l'alta velocità. ...................................................................17
Figura 1.5. Sezione della regione di solidificazione all'interno della bramma. ..22
Figura 1.6. Identificazione delle tre zone caratteristiche all'interno della sezione
della bramma. ......................................................................................................23
Figura 1.7. Evoluzione delle fasi con la temperatura. .........................................24
Figura 1.8. Evoluzione della temperatura nella regione della colata. .................25
Figura 1.9. Evoluzione della temperatura nella regione del forno di
riscaldamento. .....................................................................................................25
Figura 1.10. Risultati del calcolo della temperatura all'equilibrio. .....................26
Figura 1.11. Risultati del calcolo delle frazioni molari all'equilibrio. ................27
Figura 1.12. Distribuzione di taglia delle particelle calcolate e misurate. ..........28
Figura 1.13. Schema di un processo di colata continua con strati di scorie in
evidenza...............................................................................................................30
Figura 1.14. Modello della matrice di acciaio in solidificazione con linee
isoterme e condizioni di flusso del calore. ..........................................................32
Figura 1.15. Schema resistenze termiche. ...........................................................34
Figura 1.16 Profili di temperatura e velocità all'interno del gap. ........................35
Figura 1.17 Schema delle oscillazioni superficiali. ............................................36
Figura 1.18. Sezione della lingottiera nella direzione di colata. .........................40
Figura 1.19. Sezione orizzontale lingottiera. ......................................................41
Figura 1.20. Schema della regione degli ugelli. ..................................................43
Figura 1.21. Flow chart con modello di solidificazione 1-D e modello di
conduzione del calore nella lingottiera 2-D. .......................................................46
Figura 1.22. Formule di precipitazione. ..............................................................58
Figura 1.23. Schema della distribuzione di particelle nel modello PSG. ............60
Figura 1.24. Formula per il modello PSG per collisione. ...................................62
Figura 2.1. Andamento attività NbC in funzione della temperatura e
Temperatura critica. ............................................................................................75
Figura 2.2. Andamento della concentrazione di niobio con la temperatura. .......78
Figura 2.3. Energia libera di Gibbs in funzione del raggio di nucleazione. ........82
Figura 2.4. Raggio critico in funzione della temperatura per il NbC. .................83
Figura 2.5. Diagramma di flusso dell’accrescimento..........................................85
Figura 2.6. Nucleazione ed accrescimento da 900K a 895K nel caso del NbC. .86
Figura 2.7. Ottaedro troncato e suo sviluppo nel piano. .....................................88
Figura 2.8. Alveare di ottaedri troncati. ..............................................................88
Indice figure
Figura 2.9. Esempio semplificativo del numero siti nella superficie totale di
nucleazione. ........................................................................................................ 90
Figura 2.10. Andamento Nn in funzione dei raggi di nucleazione per NbC. ...... 92
Figura 2.11. Andamento Nn in funzione della temperatura per il NbN. ............. 93
Figura 2.12. Andamento frazioni superficie totali in funzione della temperatura
per il NbC. .......................................................................................................... 94
Figura 3.1. Ciclo termico imposto alla parte centrale del provino durante la
simulazione del secondary cooling con contatto dei rulli. A) riscaldamento
iniziale; B) mantenimento di omogeneizzazione; C) simulazione di secondary
cooling con contatto dei rulli;D) brusco raffreddamento. .................................. 97
Figura 3.2. Immagine al FEG-SEM con ingrandimento a 20.000x per la
superficie di frattura del provino 1. .................................................................. 100
Figura 3.3. Immagine al FEG-SEM con ingrandimento a 20.000x per la
superficie di frattura del provino 2. .................................................................. 101
Figura 3.4. Immagine al FEG-SEM con ingrandimento a 80.000x per la
superficie di frattura del provino 3. .................................................................. 102
Figura 3.5. Immagine al FEG-SEM con ingrandimento a 10.000x per la
superficie di frattura del provino 4. .................................................................. 103
Figura 3.6. Immagine al FEG-SEM con ingrandimento a 200.000x per la
superficie di frattura del provino 5. .................................................................. 104
Figura 3.7. Immagine al FEG-SEM con ingrandimento a 50.000x per la
superficie di frattura del provino 6. .................................................................. 106
Figura 3.8. Immagine al FEG-SEM con ingrandimento a 30.000x per la
superficie di frattura del provino. ..................................................................... 107
Figura 3.9. Immagine al FEG-SEM con ingrandimento a 120.000x per la
superficie di frattura del provino 8. .................................................................. 108
Figura 3.10. Immagine al FEG-SEM con ingrandimento a 200.000x per la
superficie di frattura del provino 9. .................................................................. 109
Figura 3.11. Immagine al FEG-SEM con ingrandimento a 50.000x per la
superficie di frattura del provino 10. ................................................................ 110
Figura 3.12. Immagine al FEG-SEM con ingrandimento a 100.000x per la
superficie di frattura del provino 11. ................................................................ 111
Figura 3.13. Immagine al FEG-SEM con ingrandimento a 10.000x per la
superficie di frattura del provino 12. ................................................................ 112
Figura 3.14. Immagine al FEG-SEM con ingrandimento a 150.000x per la
superficie di frattura del provino 13. ................................................................ 113
Figura 3.15. Distanze tra precipitati calcolate con il modello previsionale...... 114
Figura 3.16. Numerosità Nn precipitati nel provino 1 (voestalpine-0,75 m/min-9
contatti) in funzione della temperatura. ............................................................ 116
Figura 3.17. Numerosità Nn precipitati nel provino 4 (voestalpine-0,3 m/min-9
contatti) in funzione della temperatura. ............................................................ 117
Figura 3.18. Numerosità Nn precipitati nel provino 1 (voestalpine-0,75 m/min-9
contatti) in funzione dei raggi di nucleazione................................................... 118
6
Indice figure
Figura 3.19. Numerosità Nn precipitati nel provino 4 (voestalpine-0,3 m/min-9
contatti) in funzione dei raggi di nucleazione. ..................................................119
Figura 3.20. Numerosità Nn precipitati nel provino 10 (dillinger-0,75 m/min-3
contatti) in funzione della temperatura. ............................................................120
Figura 3.21. Numerosità Nn precipitati nel provino 11 (dillinger-0,5 m/min-3
contatti) in funzione della temperatura. ............................................................121
Figura 3.22. Numerosità Nn precipitati nel provino 11 (dillinger-0,5 m/min-3
contatti) in funzione dei raggi di nucleazione. ..................................................122
Figura 3.23. Frazione di superficie provini voestalpine (provini 1-2-3-4-8) in
funzione dei raggi di nucleazione. ....................................................................123
Figura 3.24. Frazione di superficie provini voestalpine (provini 1-2-3-4-8) in
funzione della temperatura. ...............................................................................125
Figura 3.25. Fraz. Sup. provini dillinger (provini 9-10-11) in funzione dei raggi.
...........................................................................................................................126
Figura 3.26. Fraz. Sup. provini dillinger (provini 9-10.11) in funzione della
temperatura. .......................................................................................................126
Figura3.27. Confronto tra risultati sperimentali e analitici del modello
previsionale, in termini di numerosità di precipitati al m2, per un range di
temperatura di [1129K-1116K] per i provini Voestalpine. ...............................127
Figura3.28. Confronto tra risultati sperimentali e analitici del modello
previsionale, in termini di numerosità di precipitati al m2, per un range di
temperatura di [1125K-1112K] per i provini Dillinger.....................................128
Figura3.29. Risultati sperimentali e analitici del modello previsionale, in termini
di frazione di superficie, per un range di temperatura di [1129K-1116K], provini
Voestalpine. .......................................................................................................129
Figura3.30. Risultati sperimentali e analitici del modello previsionale, in termini
di frazione di superficie, per un range di temperatura di [1125K-1112K],provini
Dillinger. ...........................................................................................................129
Figura3.31. Risultati sperimentali e analitici del modello previsionale, in termini
di distanza [m] tra precipitati, per un range di temperatura di [1128K-1116K],
provini Voestalpine. ..........................................................................................130
Figura3.32. Risultati sperimentali e analitici del modello previsionale, in termini
di distanza [m] tra precipitati, per un range di temperatura di [1125K-1112K],
provini Dillinger. ...............................................................................................130
Figura 4.1. Frazione di superficie percentuale al variare dell’energia di
interfaccia j, in funzione della temperatura per un provino Dillinger. ..............132
Figura 4.2. Numerosità precipitati/m2 al variare del calore latente di fusione del
carburo di niobio, in funzione della temperatura, per un provino Dillingen. ....134
Figura 4.3. Frazione di superficie percentuale, al variare della % di niobio,
tenendo fissata la % di C (0.1%), in funzione della temperatura. .....................136
Figura 4.4. Numerosità precipitati/m2 ,al variare della % di niobio, tenendo
fissata la % di C (0.1%), in funzione della temperatura....................................136
7
Indice figure
Figura 4.5. Frazione di superficie percentuale, al variare della % di carbonio,
tenendo fissa la % di Nb (0.035%), in funzione della temperatura. ................. 138
Figura 4.6. Numerosità precipitati/m2, al variare della % di carbonio, tenendo
fissata la % di Nb (0.035%), in funzione della temperatura. ............................ 138
Figura 4.7. Frazione di superficie percentuale nei casi estremi di % di C e Nb, in
funzione della temperatura. .............................................................................. 140
Figura 4.8. Raggi di nucleazione per NbC, NbN e AlN, in funzione della
temperatura. ...................................................................................................... 141
Figura 4.9. Numerosità precipitati/m2, per il NbC, NbN e AlN, in funzione della
temperatura, per un provino Dillinger. ............................................................. 142
Figura 4.10. Frazione di superficie percentuale, per il NbC, NbN e AlN, in
funzione della temperatura, per un provino Dillinger. ..................................... 143
Figura 5.1. Confronto tra risultati sperimentali e analitici del modello
previsionale, in termini di numerosità di precipitati al m2, per un range di
temperatura di [1129K-1116K] per i provini Voestalpine. .............................. 146
Figura 5.2. Confronto tra risultati sperimentali e analitici del modello
previsionale, in termini di numerosità di precipitati al m2, per un range di
temperatura di [1125K-1112K] per i provini Dillinger. ................................... 146
Figura A.1. Simulazione del dominio della matrice. ........................................ 149
Figura D.1. Coefficienti conduttività termica. .................................................. 153
Figura D.2. Calore specifico. ............................................................................ 153
Figura D.3. Coefficienti di densità. .................................................................. 154
8
Indice tabelle
Tabella 1.1. Composizione in % dell'acciaio HSLA utilizzato nell'esperimento.
.............................................................................................................................21
Tabella 1.2. Prodotti di solubilità. .......................................................................49
Tabella 1.3. Coefficienti di interazione di Wagner. ............................................51
Tabella 1.4. Gruppi di precipitati mutualmente solubili. ....................................52
Tabella 1.5. Precipitati per ogni elemento di lega. ..............................................54
Tabella 2.1. Temperature critiche di precipitazione nel caso di NbC, NbN, AlN.
.............................................................................................................................76
Tabella 2.2. Massa atomica e concentrazioni nominali di Nb, C, Al, N. ............77
Tabella 2.3. Calore latente di NbC, NbN, AlN. ..................................................80
Tabella 2.4. Volume molare di NbC, NbN, AlN. ...............................................81
Tabella 3.1. Composizione chimica (in % in peso) dei provini forniti
dall'acciaieria Dillinger. ......................................................................................96
Tabella 3.2. Composizione chimica (in % in peso) dei provini forniti
dall'acciaieria Voestalpine. Boro e azoto sono dati in ppm. ...............................96
Tabella 3.3. Piano delle prove sperimentali. .......................................................97
Tabella 3.4. Temperature e tempi adottati durante la simulazione delle modalità
di colata. ..............................................................................................................98
Tabella 3.5. Distanze tra precipitati provino 1. ................................................100
Tabella 3.6. Media, σ, σ2 provino 1.Valori in micrometri. ...............................101
Tabella 3.7. Distanze tra precipitati provino 2. .................................................102
Tabella 3.8. Media, σ, σ2 provino 2.Valori in micrometri. ...............................102
Tabella 3.9. Distanze tra precipitati provino 3. .................................................103
Tabella 3.10. Media, σ, σ2 provino 3.Valori in micrometri. .............................103
Tabella 3.11. Distanze tra precipitati provino 4. ...............................................104
Tabella 3.12. Media, σ, σ2 provino 4.Valori in micrometri. .............................104
Tabella 3.13. Distanze tra precipitati provino 5. ...............................................105
Tabella 3.14. Media, σ, σ2 provino 5.Valori in micrometri. .............................105
Tabella 3.15. Distanze tra precipitati provino 6. ..............................................106
Tabella 3.16. Media, σ, σ2 provino 6.Valori in micrometri. .............................107
Tabella 3.17. Distanze tra precipitati provino 7. ..............................................107
Tabella 3.18. Media, σ, σ2 provino 7. Valori in micrometri. ...........................108
Tabella 3.19. Distanze tra precipitati provino 8. ..............................................108
Tabella 3.20. Media, σ, σ2 provino 8.Valori in micrometri. ............................109
Tabella 3.21. Distanze tra precipitati provino 9. ...............................................109
Tabella 3.22. Media, σ, σ2 provino 9.Valori in micrometri. .............................110
Tabella 3.23. Distanze tra precipitati provino 10. .............................................110
Tabella 3.24. Media, σ, σ2 provino 10.Valori in micrometri. ...........................111
Tabella 3.25. Distanze tra precipitati provino 11. .............................................111
Indice tabelle
Tabella 3.26. Media, σ, σ2 provino 11.Valori in micrometri. .......................... 112
Tabella 3.27. Distanze tra precipitati provino 12. ........................................... 112
Tabella 3.28. Media, σ, σ2 provino 12.Valori in micrometri. ........................... 113
Tabella 3.29. Distanze tra precipitati provino 13. ........................................... 113
Tabella 3.30. Media, σ, σ2 provino 13.Valori in micrometri. .......................... 114
Tabella 3.31. Valori sperimentali di frazione di superficie e numerosità su tutti i
provini utilizzati. ............................................................................................... 115
Tabella 3.32. Frazioni di superficie per provini 1-2-3-4-8. .............................. 124
Tabella 4.1. Temperature critiche di precipitazione del NbC, in funzione della
% di niobio, tenendo fisso il valore di carbonio (0.1%). .................................. 135
Tabella 4.2. Temperature critiche di precipitazione del NbC, in funzione della %
di carbonio, tenendo fisso il valore di niobio (0.035%). .................................. 137
Tabella 4.3. Temperature critiche di precipitazione del NbC, in funzione della %
di carbonio e niobio. ......................................................................................... 139
Tabella C.1. Dati per il modello. ...................................................................... 152
10
Sommario
Gli acciai microlegati sono una categoria di materiali altamente richiesta sul
mercato e trovano largo impiego in diversi campi ingegneristici.
La caratteristica fondamentale di tali acciai è la bassa percentuale di elementi di
lega che sono presenti al loro interno (inferiori allo 0,1%), ma nonostante ciò
questi elementi condizionano fortemente il comportamento dell’acciaio in
quanto permettono la formazione di precipitati stabili che modificano la matrice
metallica nella quale sono contenuti.
Obiettivo della presente tesi è quello di realizzare un modello previsionale per la
precipitazione di alcuni precipitati di interesse, in funzione del percorso termico
che subisce l’acciaio, di conseguenza, in funzione della temperatura.
Partendo dalla conoscenza e spiegazione di metodi già esistenti in letteratura, si
è costruito un modello in grado di valutare l’andamento della numerosità e
dimensione dei precipitati, nonché di stimare la distanza che intercorre tra essi.
I risultati del modello sono stati poi confrontati con quelli di una campagna
sperimentale, in cui due tipologie di provini, con diversa composizione chimica,
hanno subito un determinato percorso termico, tipico del processo di colata
continua: tramite osservazioni delle superfici di frattura al microscopio
elettronico FEG-SEM, si sono misurati valori di numerosità e frazione di
superficie percentuale, nonché di distanza tra i precipitati che sono stati
confrontati con i valori ricavati dal modello previsionale, per la validazione
dello stesso.
Parole chiave
Colata continua, precipitati, carburi di niobio, modello termico, nucleazione,
accrescimento.
Sommario
Abstract
Microalloyed steels are a class of steels highly demand in the market and are
widely used in various engineering fields.
The key feature of these steels is the low percentage of alloying elements that
are present in them (less than 0.1%), but nevertheless these elements strongly
influence the behavior of steel as they allow the formation of stable precipitates
change matrix metal in which they are contained.
The objective of this thesis is to provide a predictive model for the precipitation
of some precipitates of interest, as a function of the thermal path which
undergoes the steel, therefore, a function of temperature.
Starting from the knowledge and explanation of methods existing in the
literature, has built a model able to evaluate the trend of the number and size of
the precipitates, as well as to estimate the distance between them.
The results of the model were then compared with those of an experimental
campaign, in which two types of specimens, with different chemical
composition, have undergone a certain thermal path, typical of the process of
continuous casting, through observations of the surfaces of fracture electron
microscopy FEG-SEM, have measured values of size and percentage fraction of
the surface, as well as the distance between the precipitates were compared with
the values obtained by the forecasting model, for the validation of the same.
Keywords
Continuous casting, precipitates, carbides of niobium, thermal model,
nucleation, growth.
12
CAPITOLO 1
Modello sulla precipitazione in acciai HSLA
(Particle-Size-Grouping Model)
1.1 Introduzione
Gli acciai micro legati ad elevata resistenza, HSLA (high-strenght low-alloy),
grazie alla loro ottima resistenza, tenacità e saldabilità trovano svariate
applicazioni in varie tipologie di costruzioni oltre che nell’industria dei trasporti
e degli autoveicoli [3].
Questi acciai HSLA contengono tipicamente meno dello 0,2% (in peso) di
carbonio, più del 2% di manganese e modeste quantità di niobio, vanadio e
titanio (solitamente inferiori allo 0,1%). I precipitati che si vengono a formare,
quali carburi e nitruri, ritardano la crescita del grano austenitico e la
ricristallizzazione, favorendo inoltre un affinamento del grano stesso,
aumentando le proprietà meccaniche dei suddetti acciai.
La precipitazione di carburi e nitruri di niobio può però anche portare alla
formazione di cricche durante alcuni processi, come in quello della colata
continua: se infatti si vengono ad accumulare elevate quantità di precipitati fini
lungo i bordi di grano ad elevate temperature, queste potrebbero causare “vuoti
locali” che concentrerebbero gli sforzi ai bordi di grano diminuendo la duttilità e
provocando rotture.
Proprio per questi motivi diventa fondamentale conoscere la forma, la
distribuzione e la frazione di volume che occupano questi precipitati (carburi e
nitruri) di niobio per determinare il comportamento degli acciai HSLA; i carbonitruri di niobio sono inoltre mutualmente solubili con quelli di titanio e vanadio
così come tutti quei precipitati che hanno una struttura cristallina cubica a facce
centrate (c.f.c.).
Tipicamente la formazione di precipitati nell’austenite indeformata, in questi
acciai, è molto lenta e occorrono dai 15-30 minuti per l’inizio e addirittura un
giorno intero per la fine completa della precipitazione.
Capitolo 1
Questo fenomeno può però essere accelerato anche di 10-1000 volte con degli
sforzi di deformazione che avvengono durante il passaggio della bramma di
acciaio attraverso i rulli nel processo di colata continua, e ciò permette di
incrementare di molto la densità delle dislocazioni, che fungono da siti di
nucleazione per i precipitati. Altro fattore che influenza la velocità di
formazione dei precipitati è il passaggio dalla fase alla fase che incrementa il
tasso di diffusione e diminuisce la solubilità di questi precipitati nella ferrite .
Di seguito, brevemente, vengono riportati i principali e caratteristici impieghi
degli acciai micro legati al niobio.
Nel campo delle saldature vengono utilizzati gli acciai HSLA poiché la presenza
di piccole quantità di niobio permette di affinare la struttura cristallina
dell’acciaio stesso e di ottenere valori di carbonio equivalente inferiori rispetto
ad un normale acciaio avente resistenza meccanica analoga [1], inoltre acciai
micro legati con niobio presentano una tenacità ed una saldabilità superiori
rispetto ai normali acciai dolci, anche per profili di saldatura molto spessi,
mantenendo buone/ottime caratteristiche in termini di resistenza meccanica.
Figura 1.1. Un esempio di processo di saldatura.
La capacità del niobio di unirsi con l'azoto a formare carbonitruri è molto
vantaggioso per quegli acciai che presentano in soluzione grandi quantità di
quest'ultimo. Diminuendo drasticamente la percentuale dell'azoto in soluzione in
tali acciai si ottiene infatti l'aumento della tenacità degli stessi e quindi della loro
saldabilità.
14
Modello sulla precipitazione in acciai HSLA (Particle-Size-Grouping Model)
Altro vantaggio che presentano questi acciai nelle saldature è che, nel momento
in cui, si desidera saldare due profili di un acciaio al manganese, occorre
preriscaldarli affinché, a saldatura avvenuta, non si producano delle cricche a
freddo in prossimità del cordone. Invece impiegando acciai microlegati al
niobio, vista la maggior tenacità, è possibile in molti casi saldare senza
preriscaldamento, con conseguenti risparmi in termini di tempo e di energia.
Per quanto concerne i valori di carico di snervamento, tipicamente per gli acciai
microlegati con niobio utilizzati nel campo delle saldature l'ottimo economico si
ha in un range di 355-460 MPa.
Altro impiego degli acciai HSLA è quello per applicazioni strutturali ad alta
resistenza dove, oltre ad elevate caratteristiche meccaniche, sono richieste anche
buone tenacità [2]. In passato il loro sviluppo in questo campo è stato promosso
come risposta nel campo degli acciai a materiali come il calcestruzzo.
A tal proposito in questi anni si stanno facendo molte ricerche per sviluppare
acciai in grado di mantenere elevate resistenze meccaniche anche ad elevate
temperature [2]. L'obiettivo è quello di realizzare acciai microlegati (tipicamente
con niobio e molibdeno) in grado di mantenere, quando portati alla temperatura
di 600°C, almeno due terzi del proprio carico di snervamento a temperatura
ambiente.
Figura 1.2. L'incendio di un grattacielo ad Astana, Kazakhistan.
15
Capitolo 1
Attualmente gli acciai strutturali, per resistere all'azione del fuoco, vengono
rivestiti con uno strato superficiale più resistente e ciò comporta un aumento dei
costi e degli ingombri. Eliminare queste protezioni comporterebbe un risparmio
di almeno il 10% sui costi costruttivi, in grado di compensare ampiamente
l'incremento di costo legato all'utilizzo di acciai microlegati resistenti all'azione
del fuoco.
Collegandomi con l’utilizzo degli HSLA negli edifici, si può affermare come
studi ed impieghi specifici di questi acciai sono rivolti a ridurre l’impatto di
uragani, terremoti e cicloni. Attualmente l'ingegneria civile richiede ai produttori
di barre di rinforzo per cemento armato di sviluppare e commercializzare acciai
in grado di sopportare allungamenti percentuali dell'ordine del 25-30%.
Alcuni acciai microlegati con niobio aventi rapporti tra il carico di rottura ed il
carico di snervamento nel range 1,28-1,30 offrono la possibilità di sostenere
efficacemente sforzi di quasi 600 MPa in corrispondenza dei livelli di
allungamento percentuale suddetti [2].
Per ottenere proprietà così notevoli, oltre al controllo della composizione
chimica è importante anche quello sul processo di tempra effettuato durante la
lavorazione degli acciai.
Un'altro impiego degli acciai microlegati con niobio si ha nelle applicazioni a
basse temperature come barre di rinforzo per cemento armato [2] in:
strutture a basse temperature di servizio (fino a -40°C nelle regioni
artiche di Canada e Russia);
muri di contenimento per serbatoi sotterranei di gas naturale liquefatto,
operanti a temperature tra i -125°C e i -100°C.
Figura 1.3. Un esempio di serbatoio sotterraneo per lo stoccaggio di gas naturale liquefatto.
16
Modello sulla precipitazione in acciai HSLA (Particle-Size-Grouping Model)
Altro utilizzo è quello nel campo ferroviario: come risultato dell'incremento dei
carichi assiali e delle velocità di esercizio dei treni, l'applicazione degli acciai
HSLA nella realizzazione di binari ferroviari è andata aumentando nel tempo.
Tali acciai si utilizzano per costruire binari aventi un'elevata resistenza alla
fatica da contatto, una notevole tenacità, una buona duttilità e saldabilità,
un’ottima resistenza a frattura, un'eccezionale resistenza all'abrasione [2].
Il niobio, grazie alla sua capacità di affinamento dei grani austenitici, crea un
rilevante rinforzo intergranulare in questi acciai, aumentando la resistenza a
frattura. Questi acciai vengono realizzati in modo da ottenere una precipitazione
uniforme in tutta la struttura dei carbonitruri di niobio, permettendo così di
intrappolare l'idrogeno presente nell'acciaio al fine di ridurne l'effetto
infragilente [2].
Figura 1.4. Treno per l'alta velocità.
Una volta compresi gli impieghi di tali acciai e quindi anche l’importanza che
riveste il fenomeno della precipitazione di carburi/nitruri al loro interno, si passa
ora a trattare dei possibili modelli previsionali che si possono utilizzare e che
permettono di simulare il fenomeno della precipitazione. Di seguito viene
proposto un modello [3] che viene utilizzato per indagare la precipitazione di
carburi/nitruri di niobio in bramme di acciai micro legati durante un processo di
colata continua, successivo riscaldamento in un forno a tunnel e quenching
(raffreddamento) finale con acqua.
Questo modello è stato sviluppato presso l’Università dell’Illinois e applicato
con una serie di esperimenti presso la Colorado School of Mines.
17
Capitolo 1
Il primo passo consiste nell’utilizzo di un modello di “trasferimento del calore”
(“heat transfer model”) per prevedere la temperatura e l’alternanza delle fasi
dell’acciaio durante il processo, per le condizioni sperimentate su i campioni
delle bramme.
Successivamente si applica un modello di precipitazione all’equilibrio
(“equilibrium precipitation model”) per prevedere le massime quantità e le
composizioni dei precipitati valutati ad ogni temperatura del processo; infine si
utilizza un modello cinetico (“kinetic model”) per valutare l’evoluzione delle
quantità di precipitati e la loro distribuzione in base alle dimensioni raggiunte.
Di seguito saranno descritti brevemente questi tre modelli, che saranno poi
approfonditi nei paragrafi successivi.
18
Modello sulla precipitazione in acciai HSLA (Particle-Size-Grouping Model)
Heat Transfer Model
La valutazione della temperatura e l’evoluzione delle fasi dell’acciaio durante la
solidificazione, colata e processo di riscaldamento è la prima parte cruciale del
modello per prevedere le microstrutture.
Nel lavoro condotto presso la Colorado School of Mines, l’equazione di
trasferimento del calore per conduzione è risolta, nelle varie zone del processo,
utilizzando il programma CON1D, in grado di calcolare il trasferimento del
calore monodimensionale all’interno della matrice di acciaio in solidificazione,
accoppiato con il trasferimento di calore in stato stazionario bidimensionale
nella lingottiera con un’attenta cura dello spazio presente tra la matrice e la
lingottiera stessa.
Al termine della lingottiera, il modello include i coefficienti di trasferimento del
calore per ogni ugello spray presente, dipendenti dalla temperatura e dalla loro
posizione nello spazio.
Dopo questa zona, il successivo riscaldamento e/o quenching può essere
aggiunto facendo ripartire la simulazione usando un profilo iniziale di
temperatura, precedentemente calcolato.
Equilibrium Precipitation Model
Un’analisi termodinamica è essenziale per prevedere la formazione dei
precipitati. Un modello è stato sviluppato per prevedere la precipitazione di 18
diversi tipi di ossidi, solfuri, nitruri e carburi che tipicamente si trovano negli
acciai micro legati.
Questo modello calcola le quantità di precipitati e le loro composizioni, per ogni
classe di acciaio e temperatura: in particolare risolve un sistema di 35 equazioni
di prodotti di solubilità grazie all’iterazione di Newton-Raphson per le quantità e
le composizioni dei precipitati di SiO2 , TiS, Ti4C2S2, AlN, BN, Cr2N e/o gruppi
di precipitati mutualmente solubili come TiNbV(CN), AlTi(O), MnMg(O) e
MnMg(S).
19
Capitolo 1
La convergenza del metodo si ottiene risolvendo sistematicamente il sistema ad
ogni temperatura, iniziando dalla temperatura più alta quando tutti i precipitati
sono disciolti e usando ogni soluzione come condizione iniziale per il passo
successivo.
Kinetic Model
I precipitati si formano in diversi momenti e posizioni durante i processi che
subisce l’acciaio: nell’acciaio liquido, per via della rapida diffusione e per le
collisioni che avvengono fra le particelle, così come nello stato solido, a causa
della lenta diffusione all’interno dei grani e quella più rapida ai bordi di grano.
Per queste motivazioni le particelle che si formano mostrano una varietà di
composizione, morfologia e distribuzione in base alle dimensioni. Così, un
modello cinetico, che descriva il tasso di precipitazione e che quantifichi
l’evoluzione delle dimensioni delle particelle con il tempo, è essenziale per
effettuare delle previsioni realistiche, specialmente per i carbonitruri.
Alcuni modelli dividono il fenomeno della precipitazione in differenti “stadi”: la
nucleazione, la crescita e l’ingrossamento con differenti equazioni associate ai
diversi stadi con molte assunzioni, semplificazioni e parametri empirici.
La nucleazione comprende un periodo di induzione per formare nuclei stabili,
seguito da una nucleazione in stato stazionario al termine della quale le
particelle subiscono un processo di crescita a causa dell’alta saturazione.
Al termine di nucleazione e crescita, le particelle di diverse dimensioni sono
disperse nella matrice e una volta che la saturazione decresce verso l’equilibrio
avviene l’ingrossamento delle stesse particelle.
L’ingrossamento è favorito dalla differenza in concentrazione dei gradienti
vicino ai precipitati di diverse dimensioni: le particelle più grandi sono
circondate da una bassa concentrazione e crescono per diffusione circondando le
particelle più piccole che sono meno stabili e si restringono.
20
Modello sulla precipitazione in acciai HSLA (Particle-Size-Grouping Model)
Un nuovo modello numerico PSG (particle-size-grouping) è stato sviluppato
per simulare la formazione dei precipitati durante i processi a cui si
sottopongono gli acciai micro legati con tempi computazionali ragionevoli.
Questo modello può prevedere l’evoluzione delle quantità di precipitati, le
dimensioni e le composizioni per una data storia temporale e include gli stadi di
nucleazione, crescita ed ingrossamento in un unico modello; quest’ultimo
simula la crescita per diffusione e dissociazione, includendo l’influenza della
minimizzazione dell’energia superficiale inclusa nel modello all’equilibrio.
Modelli pratici possono simulare particelle di dimensioni comprese tra 0,1nm e
100m. Con il modello PSG si divide l’intero range di particelle di diversa
dimensione in un piccolo numero di gruppi dimensionali, con una grandezza
caratteristica per ogni gruppo.
Inoltre, invece che calcolare le interazioni fra le particelle di ogni dimensione, il
metodo PSG considera le interazioni solo tra gruppi dimensionali, calcolando la
densità numerica per ognuno di essi.
Recentemente, un nuovo modello PSG con un’accuratezza migliore è stato
sviluppato monitorando anche i valori delle dimensioni delle particelle nelle
zone limitrofe ai “bordi del gruppo dimensionale”.
Per valutare la bontà di questo metodo viene di seguito proposta la descrizione
di un esperimento effettuato su una bramma di acciaio HSLA.
Esperimento
L’esperimento in questione riguarda una sottile bramma di acciaio HSLA,
1200mm x 50mm, durante il processo di colata continua alla velocità di colata di
5 m/min. La composizione (% in peso) dell’acciaio è quella di seguito riportata
in tabella 1.1.
Tabella 1.1. Composizione in % dell'acciaio HSLA utilizzato nell'esperimento.
C
0,031
Ni
0,031
Si
0,194
V
0,001
Mn
1,039
S
0,003
Cr
0,032
P
0,012
Mo
0,01
Nb
0,046
Ti
0,003
N
0,006
Al
0,031
21
Capitolo 1
La lingottiera ha una lunghezza di lavoro di 850mm e la zona di raffreddamento
secondaria, dove sono presenti gli ugelli spray dell’acqua, si estende dal termine
della lingottiera fino a 6 metri sotto il menisco.
La tipica temperatura registrata della superficie della bramma all’uscita
dell’ultima coppia di rulli della “spray zone” è di 800°C.
La bramma poi prosegue alcuni metri per poi venire nuovamente riscaldata
raggiungendo una temperatura sulla superficie di 980°C in un forno dalla
temperatura interna di 1080°C.
Figura 1.5. Sezione della regione di solidificazione all'interno della bramma.
Dalla bramma vengono poi prelevati dei campioni di 700mm di lunghezza, i
quali vengono sottoposti al fenomeno rapido del quenching (raffreddamento in
acqua agitata alla temperatura ambiente) e infine tagliati in pezzi di piccole
dimensioni, 300mm x 125mm x 50mm.
I campioni vengono poi disciolti in due stadi successivi per separare e misurare i
precipitati di Nb dal Nb rimasto in soluzione.
A questo punto, i precipitati vengono contati in sezioni particolari e si valuta le
composizioni per determinare la distribuzione degli stessi in base anche alle
dimensioni.
22
Modello sulla precipitazione in acciai HSLA (Particle-Size-Grouping Model)
Come mostrato in fig.1.6 si identificano tre differenti “porzioni” di volume
all’interno della bramma: una zona vicina alla superficie (chill zone, S), una
zona colonnare a media profondità (columnar zone, M) e una zona equiassica
vicina al centro della bramma (central equiaxed zone, C).
Figura 1.6. Identificazione delle tre zone caratteristiche all'interno della sezione della
bramma.
Tre differenti prove sono state effettuate con rispettivamente una bassa, media,
alta aggiunta di niobio. Ogni campione di acciaio è stato disciolto in soluzione
acquosa al 5% di acido cloridrico e al 3% di acido tartarico e filtrato per
separare la matrice di acciaio disciolta dai precipitati in lega.
Gli esperimenti hanno mostrato come l’estensione dei precipitati aumenta con
l’aumentare delle aggiunte di Nb.
23
Capitolo 1
La precipitazione maggiore avviene sulla superficie della bramma, in cui lo
scioglimento si verifica in seguito al riscaldamento nel forno. La regione
colonnare comprende la maggior parte del volume della bramma e presenta la
più bassa quantità di precipitati di Nb.
Sulla superficie i precipitati presentano una forma cuboidale e cuboidale
irregolare con dimensioni relativamente piccole (10-30nm), mentre nella regione
colonnare e al centro si presentano di dimensioni maggiori.
Risultati esperimento
Il modello di trasferimento del calore, CON1D, è usato per prevedere la
temperatura e la storia delle fasi. La temperatura dell’acciaio liquido è assunta
pari a 1553°C. I tassi di trasferimento del calore dell’acqua spray sono regolati
in modo che corrispondano le temperature di uscita dalla colata (800°C) e di
ingresso del forno di riscaldamento (980°C).
Il coefficiente di convezione per l’aria è assunto pari a 8,7 W*m-2*K-1 e il
coefficiente per il trasferimento di calore per l’acqua agitata è 2000 W*m-2*K-1.
Le seguenti fig.1.7,1.8,1.9 mostrano l’evoluzione delle fasi al variare della
temperatura e l’andamento della temperatura all’interno della bramma.
Figura 1.7. Evoluzione delle fasi con la temperatura.
24
Modello sulla precipitazione in acciai HSLA (Particle-Size-Grouping Model)
Figura 1.8. Evoluzione della temperatura nella regione della colata.
Figura 1.9. Evoluzione della temperatura nella regione del forno di riscaldamento.
Sulla superficie della bramma la temperatura diminuisce rapidamente nelle zone
della lingottiera e del raffreddamento dell’acqua spray, mentre aumenta
25
Capitolo 1
all’uscita della zona di raffreddamento secondario a causa del calore presente
ancora all’intero della bramma, che tende ad equilibrare la distribuzione di
temperatura. La temperatura diminuisce poi ancora a causa del raffreddamento
con l’aria prima di risalire con l’entrata nel forno di riscaldamento, dove, dopo
un iniziale incremento, si attesta ad un valore costante per poi decrescere
rapidamente a contato con l’acqua durante il quenching.
La temperatura all’interno della bramma invece decresce in modo molto più
lento nella lingottiera e nella zona degli ugelli, continuando poi a diminuire a
contatto con l’aria. Come per quella della superficie, anche la temperatura
interna aumenta ad un valore costante nel forno per poi diminuire nuovamente
con il quenching.
Il modello sulla precipitazione all’equilibrio è usato invece per prevedere le fasi
all’equilibrio come funzione della temperatura, basandosi sulla composizione
dell’acciaio e sulle fasi della matrice, derivanti dal modello di trasferimento del
calore.
Figura 1.10. Risultati del calcolo della temperatura all'equilibrio.
Per questo acciaio, il solfuro di Mn inizia a precipitare a 1508°C in fase , si
scioglie parzialmente durante il passaggio in austenite perché il limite di
solubilità di questo solfuro è maggiore nell’austenite che nella faseCon il
diminuire della temperatura, i carburi e nitruri di Ti, Nb e V precipitano da
26
Modello sulla precipitazione in acciai HSLA (Particle-Size-Grouping Model)
1289°C mentre il nitruro di Al da 1039°C in austenite; la precipitazione proprio
di AlN è ritardata dalla formazione degli altri nitruri/carburi per il fatto che essi
richiedono un certo consumo di azoto.
Figura 1.11. Risultati del calcolo delle frazioni molari all'equilibrio.
Il grafico di fig.1.11 mostra l’andamento delle frazioni molari al variare della
temperatura: alle alte temperature, TiN è il composto più stabile. Con il
diminuire della temperatura, si formano più carburi ed è presente più carbonio
che azoto nell’acciaio. Interessante notare come la frazione di NbN aumenti per
poi diminuire con la temperatura raggiungendo un massimo a 1050°C.
Infine il modello cinetico viene utilizzato per prevedere l’evoluzione della
distribuzione dimensionale dei precipitati nei campioni misurati. Il diametro
limite dei precipitati utilizzato per definire la distribuzione è stato troncato a
4nm.
Sulla superficie della bramma, i carburi/nitruri di Nb iniziano a precipitare
durante la colata continua raggiungendo un massimo alla fine della zona di
raffreddamento secondario. Successivamente, almeno principalmente, si
sciolgono a causa del calore proveniente dall’interno della bramma. All’interno
della regione colonnare, non sono previste precipitazioni rilevanti di
carburi/nitruri di Nb fin dopo il riscaldamento e il quenching. Siccome il centro
27
Capitolo 1
della bramma si raffredda invece più lentamente della regione colonnare i
precipitati di Nb si concentrano principalmente in questa zona.
Nella seguente fig.1.12 sono confrontate le distribuzioni di particelle misurate e
calcolate in base alle dimensioni.
Figura 1.12. Distribuzione di taglia delle particelle calcolate e misurate.
Le dimensioni calcolate sono molto più piccole di quelle misurate e la
previsione si avvicina di più alla realtà sulla superficie della bramma, dove la
dimensione media prevista di 11nm può essere comparata con quella misurata di
24nm e anche la forma della distribuzione è simile.
Le misurazioni mostrano che le dimensioni aumentano con la distanza dalla
superficie verso le regioni centrali e il calcolo con il modello non riesce a
mostrare questo comportamento.
28
Modello sulla precipitazione in acciai HSLA (Particle-Size-Grouping Model)
Queste particelle di dimensioni maggiori possono formarsi per differenti ragioni:
temperatura leggermente inferiore a quella prevista, durante il
riscaldamento, che potrebbe aumentare il tasso di precipitazione di
alcuni ordini di grandezza
la diffusione è più veloce lungo i bordi di grano rispetto all’interno della
matrice metallica
l’energia di interfaccia tra particelle e matrice varia con la temperatura
durante la precipitazione
questo modello non tiene in considerazione le precipitazioni di TiN, che
sono molto stabili e promuovono la precipitazione nel forno di
riscaldamento
Ricapitolando questo modello globalmente risulta quindi costituito da un HEAT
TRANSFER MODEL, per la previsione della temperatura e delle fasi durante i
processi, un EQUILIBRIUM PRECIPITATION MODEL, per la previsione
delle quantità, della stabilità e della composizione dei precipitati all’equilibrio e
un KINETIC MODEL, per la previsione delle distribuzioni delle particelle in
base alle dimensioni includendo la transizione tra nucleazione, crescita ed
ingrossamento: alla luce delle analisi effettuate questo modello è in accordo
qualitativamente con i risultati sperimentali, pur sottostimando le dimensioni
misurate con valori medi di 24nm, 72nm, 91nm rispettivamente sulla superficie,
nella regione colonnare e nella regione centrale.
Nei prossimi paragrafi si andranno ad analizzare singolarmente nel dettaglio i tre
modelli:
-
Heat Transfer Model
Equilibrium Precipitation Model
Kinetic Model
29
Capitolo 1
1.2 Heat Transfer Model
Nel seguente paragrafo l’obiettivo è quello di entrare nel dettaglio di come si
applica il modello di trasferimento del calore in un processo di colata continua
di bramme.
Il modello [4] riesce a prevedere lo spessore della matrice metallica, la
distribuzione di temperatura nella lingottiera, oltre che nella matrice ed altri
fenomeni correlati con essi.
Il trasferimento di calore nel processo di colata continua ed in particolare nella
zona della lingottiera, è governato da molti fenomeni complessi ed alcuni di
questi sono rappresentati schematicamente nella fig.1.13.
Figura 1.13. Schema di un processo di colata continua con strati di scorie in evidenza.
30
Modello sulla precipitazione in acciai HSLA (Particle-Size-Grouping Model)
Il flusso di acciaio liquido all’interno della cavità della lingottiera attraverso lo
scaricatore è funzione della geometria dello stesso. L’acciaio liquido solidifica a
contatto con le quattro pareti della lingottiera di rame raffreddata con acqua,
mentre tende a scendere verso il basso con una determinata velocità di colata.
La polvere, aggiunta sulla superficie libera dell’acciaio liquido, si scioglie e
scorre tra l’acciaio stesso e la parete della lingottiera per agire come lubrificante;
questa polvere, quando solidifica (e prende il nome di scoria), si raffredda
adiacente alla parete della lingottiera e aumenta in viscosità. Questa è più spessa
vicino e appena sopra il menisco dove è chiamata “anello di scoria” (in inglese
“slag rim”).
La scoria si raffredda rapidamente contro la parete della lingottiera, formando
un sottile strato solido vetroso, che può devetrificare per formare uno
strato cristallino se il tempo di permanenza nella lingottiera è particolarmente
lungo. Questo strato, spesso, rimane incollato alla lingottiera anche se a volte
viene trascinato ad intermittenza verso il basso ad una velocità media inferiore a
quella di colata. Gli strati di scorie conferiscono una grande resistenza alla
rimozione del calore, anche se forniscono uniformità rispetto all'alternativa di
avere un gap intermittente di vapore.
La conduzione di calore attraverso la scoria dipende dallo spessore e dalla
conducibilità degli strati, che, a loro volta, dipendono dal profilo di
velocità, temperatura
di
cristallizzazione, dalla
viscosità
e
stato
(vetroso, cristallino, o liquido) della scoria.
Lo stato può essere ricavato dai diagrammi di trasformazioni TTT per la scoria,
conoscendo il tasso di raffreddamento locale. La conduttività invece dipende
anche dal grado di cristallizzazione e dall’evoluzione interna dei gas disciolti per
formare le bolle (bubbles).
Il restringimento della matrice di acciaio lontano dalle pareti della lingottiera
può generare resistenze di contatto o gap di aria, che fungono da ulteriore
resistenza al flusso di calore; in particolare dopo che la scoria è completamente
solida ed in grado di fluire negli interstizi.
Le ondulazioni superficiali presenti sulla bramma, dipendono dalla tendenza
della matrice di "incresparsi" durante la solidificazione in corrispondenza del
menisco per formare una superficie irregolare con segni di profonde
“oscillazioni”.
Infine, il flusso di acqua di raffreddamento attraverso le fessure verticali della
lingottiera di rame diminuisce il calore e controlla la temperatura delle pareti.
31
Capitolo 1
All'uscita della lingottiera, la matrice di acciaio si muove tra serie successive
di rulli di supporto alternati ad ugelli che spruzzano acqua sulla superficie della
bramma in solidificazione. L'estrazione del calore che segue provoca
variazioni di temperatura in superficie mentre la matrice continua a solidificare.
Formulazione del modello
Il modello calcola il flusso di calore in transitorio monodimensionale attraverso
la matrice in solidificazione, accoppiato con la conduzione del calore in stato
stazionario bidimensionale all’interno delle pareti della lingottiera. Il
surriscaldamento dell’acciaio liquido si modella come una fonte di calore per
l’interfaccia solido/liquido dell’acciaio e il modello simula il comportamento
assiale (z) sotto una posizione scelta sul perimetro della lingottiera.
Figura 1.14. Modello della matrice di acciaio in solidificazione con linee isoterme e
condizioni di flusso del calore.
32
Modello sulla precipitazione in acciai HSLA (Particle-Size-Grouping Model)
Conduzione del calore nella matrice di acciaio
La temperatura nella matrice è governata da un’equazione della conduzione del
calore in transitorio monodimensionale che diventa la seguente nel momento in
cui la conduttività ksteel dipende dalla temperatura stessa:
(1.1)
Le proprietà dipendenti dalla temperatura sono riportate in APPENDICE, così
come la soluzione esplicita dell’eq.(1.1), comprese le condizioni al contorno.
L’eq.(1.1) assume che la conduzione di calore in direzione assiale (z) è
trascurabile nell’acciaio.
Il dominio di questa porzione del modello è una sezione che comprende
l'acciaio liquido e la matrice solida, che si muovono verso il basso alla velocità
di colata, come illustrato nella fig.1.14, insieme con le condizioni tipiche di
interfaccia.
Trasferimento del calore nel gap tra matrice e lingottiera
Il trasferimento di calore attraverso il gap governa il flusso di calore che lascia
l’acciaio, qint, per entrare nella lingottiera. Per calcolare questo flusso in ogni
posizione lungo la lingottiera, il modello valuta un effettivo coefficiente (hgap),
tra la temperatura della superficie della matrice d’acciaio (Ts) e quella della
parete della lingottiera (Tmold):
(1.2)
33
Capitolo 1
(1.3)
Dove rcontact è la resistenza al contatto scoria/lingottiera (m2K/W). La
conduzione di calore dipende dalle resistenze termiche dei quattro diversi
strati di materiali contenuti nel gap: le oscillazioni superficiali della matrice,
scorie liquide, scorie solide e un possibile gap di aria.
Le resistenze termiche dipendono dai profili medi di spessore nel tempo lungo la
lingottiera dei differenti strati e dalle loro conducibilità termiche, come illustrato
nelle fig.1.15 e fig.1.16.
Figura 1.15. Schema resistenze termiche.
34
Modello sulla precipitazione in acciai HSLA (Particle-Size-Grouping Model)
Figura 1.16 Profili di temperatura e velocità all'interno del gap.
Le resistenze più importanti sono quelle relative agli strati di scorie ed il calcolo
del loro spessore sarà descritto in seguito.
Il gap d’aria (dgap) viene assunto come dato. Tutte le “ondulazioni” nella
superficie della matrice sono incorporate nel modello attraverso la profondità
(dmark) e larghezza (Lmark) di oscillazione, come illustrato nella seguente fig.1.17.
35
Capitolo 1
Figura 1.17 Schema delle oscillazioni superficiali.
Assumendo queste oscillazioni, poco profonde e a forma di triangolo , si calcola
dosc , che è la profondità di tali oscillazioni basato sui volumi medi:
(1.4)
Dove Lpitch (m) è la distanza tra due oscillazioni successive.
Queste
“increspature”
influenzano
il
trasferimento
di
calore in due modi diversi: in primo luogo, consumano la scoria e il suo
spessore, in secondo luogo, esse riducono efficacemente la conduzione di calore
da fornire ad uno spazio aggiuntivo. Questo spazio supplementare è
caratterizzato da deff:
(1.5)
36
Modello sulla precipitazione in acciai HSLA (Particle-Size-Grouping Model)
(1.6)
Questi “segni” di oscillazione si suppone essere riempiti di scorie, aria o una
miscela, a seconda della temperatura della superficie della matrice. Così viene
regolato il valore di kmark.
Per quanto riguarda il coefficiente dovuto alla radiazione, hrad, la seguente
eq.(1.7) mostra come viene calcolato:
Dove m è l’indice di rifrazione della scoria, TsK è la temperatura dalla parte del
lato “caldo” dello strato di scoria liquida misurata in Kelvin, TfsolK è la
temperatura di solidificazione della scoria lato lingottiera misurata anch’essa in
Kelvin, é il coefficiente di assorbimento medio della scoria, assumendo la
radiazione di un corpo grigio (slag = 0,9). Nel caso in cui la scoria liquida si
esaurisse così che Ts < Tfsol, allora hrad = 0. In caso contrario nell’eq.(1.7) si
utilizzano Tmold e mold al posto di Tfsol e slag.
Bilancio di massa e quantità di moto sugli strati di scorie
La scoria si assume scenda lungo il gap come due strati distinti: scoria solida e
scoria liquida. Si assume che lo stato solido si muova ad una velocità media
(Vsolid), che è sempre compresa tra zero e la velocità di colata, in accordo con la
misura empirica dei loro rapporti (fv).
37
Capitolo 1
(1.8)
La viscosità della scoria fusa (T), si presume che vari esponenzialmente con
la temperatura:
(1.9)
Dove i parametri Tfsol e
sono scelti empiricamente per contenere i dati
misurati e è la viscosità misurata ad una temperatura di riferimento, T0, di
solito scelta a 1300°C.
Utilizzando le ultime due eq.(1.8) e (1.9) si ricava una velocità media per lo
strato di scoria liquida:
(1.10)
Dove s è la viscosità della scoria all’interfaccia scoria liquida/matrice
metallica.
Un bilancio di massa viene imposto in modo che corrisponda il valore
misurato di consumo di polvere, Qslag (kg/m2), con il tasso totale di flusso della
scoria fusa passato in ogni posizione lungo il gap. Tale consumo è espresso
nella seguente eq.(1.11) dove compare il consumo per massa di prodotto
(Mslag (kg / ton)).
(1.11)
Dove W è la larghezza della bramma e N è lo spessore della bramma.
38
Modello sulla precipitazione in acciai HSLA (Particle-Size-Grouping Model)
La scoria può essere trasportata verso il basso dallo strato solido, lo strato
liquido e dalle ondulazioni sulla matrice:
(1.12)
Gli spessori degli strati solidi e liquidi sono quindi ottenuti risolvendo
un’equazione polinomiale di quarto ordine, ottenuta combinando le eq.(1.3) e
eq.(1.12).
Conduzione del calore nella lingottiera
Per la conduzione di calore nella lingottiera, in 2 dimensioni, la temperatura di
regime all'interno di una sezione rettangolare verticale attraverso la porzione
superiore della lingottiera viene calcolata assumendo conducibilità costante:
(1.13)
L’eq.(1.13) si risolve applicando come soluzione una serie di prodotti di Fourier,
applicando un fissato flusso di calore :
qint = - kmold* (T/x)
(1.14)
e convezione, hwater, e la Twater come condizione al contorno, come mostrato in
fig.1.18.
39
Capitolo 1
Figura 1.18. Sezione della lingottiera nella direzione di colata.
Questo dominio è generalmente scelto per estendersi dalla parte superiore della
lingottiera fino a 100 mm al di sotto del menisco. Sotto questa zona del
menisco, il flusso di calore è monodimensionale attraverso lo spessore. La
temperatura in corrispondenza della faccia calda di rame (Thotc) è allora:
(1.15)
Dove dmold è lo spessore della lingottiera calcolato nell’APPENDICE.
Per questo calcolo si rendono necessari anche Twater, la temperatura iniziale
dell’acqua, e il coefficiente di trasferimento del calore effettivo dell’acqua,
hwater, discussi in seguito.
40
Modello sulla precipitazione in acciai HSLA (Particle-Size-Grouping Model)
Convezione dell’acqua di raffreddamento
Il coefficiente di scambio termico tra l'acqua di raffreddamento e la faccia
fredda ("lato acqua") della lingottiera è calcolato per includere una possibile
resistenza dovuta ai depositi calcarei sulla superficie dei canali di
raffreddamento dell’acqua con hfin calcolato con l’ eq.(1.17):
(1.16)
(1.17)
Dove i parametri geometrici Lch, wch e dch sono mostrati nella fig.1.19.
Figura 1.19. Sezione orizzontale lingottiera.
41
Capitolo 1
Il coefficiente di trasferimento del calore tra l’acqua e i lati dei canali
dell’acqua (hw), è calcolato assumendo flusso turbolento attraverso un diametro
equivalente usando la correlazione empirica di Sleicher e Reusse:
(1.18)
Dove il diametro equivalente del canale di acqua è dato dal’eq.(1.19):
(1.19)
E dove c1 e c2 sono costanti empiriche:
(1.20)
(1.21)
42
Modello sulla precipitazione in acciai HSLA (Particle-Size-Grouping Model)
Zona di raffreddamento secondario (zona ugelli)
Sotto la lingottiera, il flusso di calore dalla superficie varia notevolmente tra
ciascuna coppia di rulli di supporto, secondo il raffreddamento degli ugelli
spray, basato sul flusso d'acqua (hspray); radiazioni (hrad-spray); convezione
naturale (hconv) e la conduzione di calore ai rulli (hroll), come mostrato
nella seguente fig1.20.
Figura 1.20. Schema della regione degli ugelli.
Tenendo conto di questi fenomeni, il modello permette di simulare il
trasferimento di calore durante l'intero processo di colata continua. L'estrazione
del calore a causa degli ugelli d'acqua è una funzione del flusso di acqua nella
seguente forma:
(1.22)
43
Capitolo 1
Dove Qwater (L/m2*s) è il flusso d’acqua nelle zone degli ugelli e Tspray è la
temperatura dell’acqua spruzzata sulla bramma. Nella correlazione empirica di
Nozaki, A=0,3925; c=0,55; b=0,0075 che sono stati utilizzati con successo
anche da altri modellatori.
La radiazione viene così calcolata:
(1.23)
Dove Tamb è la temperatura ambiente e TsK e TambK sono la temperatura di
superficie e quella ambiente espresse in gradi Kelvin, è la costante di Stephan
Boltzman, è l’emissività.
La convezione naturale è trattata come una costante per ogni zona spray e per il
solo raffreddamento ad acqua è pari a 8,7 W/m2K.
L’estrazione del calore nella zona dei rulli è calcolata basandosi sulla frazione di
calore estratto dai rulli (froll), che è calibrato per ogni zona:
Un tipico valore di froll di 0,05 produce una caduta di temperatura sotto i rulli di
circa 100°C.
44
Modello sulla precipitazione in acciai HSLA (Particle-Size-Grouping Model)
Soluzione metodologica
Il modello richiede la risoluzione simultanea di tre diversi sistemi di equazioni:
la conduzione del calore in transitorio monodimensionale della matrice
d’acciaio, la conduzione del calore nella lingottiera in stato stazionario
bidimensionale e le equazioni di bilancio di massa, calore e quantità di moto nel
gap tra matrice e lingottiera.
La simulazione inizia impostando le temperature iniziali dell’acciaio e della
lingottiera rispettivamente alle temperature di liquidus e di ingresso dell’acqua
di raffreddamento.
Allora, ad ogni istante di tempo, si comincia riordinando e risolvendo le eq.(1.3)
e eq.(1.12) simultaneamente per trovare dliquid e dsolid, basandosi sul bilancio di
calore e massa al tempo precedente. Il flusso di calore qint è quindi calcolato in
accordo con le eq.(1.2) e eq.(1.3), che rappresentano la condizione al contorno
sia per il dominio dell’acciaio sia per la lingottiera.
Il coefficiente hwater è calcolato attraverso le eq.(1.16), eq.(1.17), eq.(1.18) ed è
usato per ottenere le temperature della lingottiera. Il modello usa un algoritmo
per risolvere l’eq.(1.1) per la temperatura della matrice ad ogni istante di tempo
(APPENDICE). Questo limita il massimo passo di tempo (dt).
I risultati sono usati come condizione iniziale per il calcolo relativo alla
lingottiera bidimensionale, che risolve l’eq.(1.13) analiticamente.
Successivamente, l'intero modello 1-D di solidificazione della matrice è
ricalcolato nella regione della lingottiera in 2-D, utilizzando le nuove
temperature della lingottiera 2-D come condizione al contorno. Questa
procedura si alterna finché le temperature della lingottiera 1-D convergono ai
risultati del 2-D entro 3°C. Questo produce una previsione che è stabile per
tutte le simulazioni esaminate e converge di solito in tre o quattro iterazioni.
La seguente figura riporta un diagramma di flusso dell'intera procedura.
45
Capitolo 1
Figura 1.21. Flow chart con modello di solidificazione 1-D e modello di conduzione del
calore nella lingottiera 2-D.
46
Modello sulla precipitazione in acciai HSLA (Particle-Size-Grouping Model)
Il modello è stato incorporato in un programma FORTRAN, CON1D.
Il programma comprende diverse scelte per le proprietà
compresi dei semplici input costanti imponibili dall'utilizzatore.
dell'acciaio,
Per default, la temperatura di liquidus, temperatura di solidus, la frazione di
fase, conduttività termica, calore specifico e di dilatazione termica lineare sono
tutte calcolate come funzioni di composizione e temperatura.
La densità di acciaio (steel), calore
superficie dell’acciaio sono costanti.
latente (Lf)
e
l’emissività
della
Per esempio per acciaio al carbonio, steel = 7400kg/m3, Lf= 271 kJ /kg
steel=0.8.
e
Informazioni dettagliate sul calcolo dei precedentemente citati parametri sono
riportate nelle varie sezioni dell’APPENDICE.
47
Capitolo 1
1.3 Equilibrium Precipitation Model
Questo modello [5] prevede la composizione e la quantità di precipitati stabili
per acciai microlegati nelle fasi liquida, ferritica e austenistica ad ogni
temperatura, sulla base dei prodotti di solubilità raccolti in un database di
possibili reazioni. Il database comprende 18 differenti precipitati e 13 elementi
chimici.
Prodotti di Solubilità
Ogni reazione di elementi M ed X dà un precipitato solido MxXy:
(1.25)
Il prodotto di solubilità all’equilibrio, dipendente dalla temperatura, K è definito
nel seguente modo espresso dall’eq.(1.26):
(1.26)
dove aM, aX, e aMxXy sono le attività di M, X e MxXy, rispettivamente.
Alcuni prodotti di solubilità sono presenti nella seguente tabella 1.2.
48
Modello sulla precipitazione in acciai HSLA (Particle-Size-Grouping Model)
Tabella 1.2. Prodotti di solubilità.
49
Capitolo 1
Per il basso contenuto di soluto negli acciai, l’attività ai per ogni elemento i
(percentuale in peso) è definita utilizzando la legge di Henry:
(1.27)
Dove
si ricava dall’utilizzo della seguente eq.(1.28):
(1.28)
i è il coefficiente di attività, eij è il coefficiente di interazione di Wagner
dell’elemento i influenzato dall’elemento di lega j e [pct i] è la concentrazione
della massa disciolta dell’elemento i.
La sommatoria “copre” le interazioni tra tutti gli elementi di lega.
In soluzioni molto diluite i coefficienti di interazione sono indipendenti dalla
fase e sono riassunti nella tabella 1.3.
50
Modello sulla precipitazione in acciai HSLA (Particle-Size-Grouping Model)
Tabella 1.3. Coefficienti di interazione di Wagner.
Durante le trasformazioni di fase, il prodotto di solubilità è definito attraverso un
peso medio basato sulla frazione di fase:
Dove fl,f, fe f sono le frazioni di fase del liquido, della ferrite , dell’austenite
e della ferrite .
51
Capitolo 1
Sebbene molti precipitati non siano solubili con altri, alcuni gruppi sono
mutualmente solubili tra loro. Le attività dei precipitati che non sono solubili
con altri rimangono unitarie, mentre quelli solubili hanno valori inferiori
all’unità perché appaiono sempre insieme con altri precipitati. Le loro attività
sono rappresentate dalle loro rispettive frazioni molari nel mix di precipitati,
così che la somma di tutte le attività appartenenti ad un “gruppo” mutualmente
solubile, raggiunga l’unità. I precipitati con la stessa struttura cristallina e
parametri di reticolo simili sono assunti come mutualmente solubili: i 18
precipitati scelti in questo lavoro sono divisi in 10 gruppi: (Ti,Nb,V)(C,N),
(Al,Ti)O, (Mn,Mg)O, (Mn,Mg)S, SiO2, TiS, Ti4C2S2, AlN, BN, Cr2N.
I gruppi di precipitati mutualmente solubili sono presenti nella tabella 1.4.
Tabella 1.4. Gruppi di precipitati mutualmente solubili.
I 18 limiti di solubilità seguono la seguente eq.(1.30):
(1.30)
dove l’attività del precipitato è determinata differentemente per i precipitati
solubili e non: il suo valore è 1 per i sei precipitati non solubili, mentre per i
quattro solubili le attività devono soddisfare le seguenti relazioni:
(1.31)
(1.32)
52
Modello sulla precipitazione in acciai HSLA (Particle-Size-Grouping Model)
(1.33)
(1.34)
Bilancio di massa
Il totale delle frazioni molari di ogni gruppo di precipitati nell’acciaio è dato
dall’eq.(1.35):
(1.35)
Le eq.(1.36/37) devono essere soddisfatte per ognuno dei 13 elementi di lega, su
tutti i 18 tipi di precipitati come riassunto nella tabella 1.5.
(1.36)
(1.37)
Dove
M0 = Asteel*M0/(100*AM)
(1.38)
[M] = Asteel*[M]/(100*AM)
(1.39)
53
Capitolo 1
sono le frazioni molari della concentrazione totale di massa, M0 (in peso),
dell’elemento dato nella composizione dell’acciaio e [M] per la concentrazione
disciolta. Asteel e AM sono le masse atomiche della matrice d’acciaio.
Relazioni analoghe valgono per l’eq.(1.40) dove la frazione molare MxXy è il
prodotto tra l’attività di questo precipitato e la frazione molare del suo gruppo
corrispondente:
(1.40)
Tabella 1.5. Precipitati per ogni elemento di lega.
Generalmente, ci sono P equazioni per i limiti di solubilità di P precipitati, M
equazioni per il bilancio di massa di M elementi di lega, e Q extra-equazioni per
i Q gruppi di precipitati mutualmente solubili: il numero totale di equazioni è
P+M+Q.
Allora, il numero totale di incognite è M+Q+P. Il seguente studio comprende
P=18 precipitati, M=13 elementi di lega e Q=4 gruppi di mutua solubilità, dando
35 equazioni in 35 incognite.
54
Modello sulla precipitazione in acciai HSLA (Particle-Size-Grouping Model)
Soluzione numerica
Partendo dalla temperatura più alta nell’acciaio liquido, la temperatura è
abbassata ad ogni istante di tempo, usando i risultati del passo precedente come
condizione iniziale per il successivo.
La concentrazione molare del precipitato può essere trasformata nella
concentrazione di massa o frazione di volume nell’acciaio: per il precipitato
MxXy, la sua concentrazione di massa wMxXy (in peso) e la sua frazione di
volume vMxXy sono calcolate a partire dalla sua frazione molare MxXy.
(1.41)
(1.42)
dove Asteel e AMxXy sono le masse atomiche e steel e MxXy sono le densità
rispettivamente della matrice di acciaio e del precipitato.
Per i semplici sistemi di precipitati singoli, come il NbN, l’interazione di
Wagner può essere trascurata e le attività degli elementi sono uguali alla loro
concentrazione.
Usando come esempio per l’appunto il NbN, il primo precipitato si forma
quando il prodotto delle concentrazioni iniziali, Nb0 e N0, supera KNbN. Dopo
che si è formato NbN, il limite di solubilità richiede:
(1.43)
55
Capitolo 1
La condizione stechiometrica per questa reazione chimica è espressa
dall’eq.(1.44):
(1.44)
e la soluzione analitica può essere sintetizzata come segue:
(a) Ad alte temperature, quando Nb0 * N0 < KNbN, non ci sono precipitati.
(b) A temperature più basse, quando Nb0 * N0 > KNbN,
(1.45)
(1.46)
(1.47)
Per precipitati non mutualmente solubili (con y/x=1), se questi non contengono
alcun elemento di lega, la soluzione analitica è semplicemente data da due set di
equazioni come quelle per il NbN. In alternativa se possiedono un’altro
elemento di lega, come nel sistema Nb – Al – N con NbN e AlN, tutte le
possibili condizioni sono testate per trovare quale precipitato si formi per primo.
Dopo che se ne è formato uno, la concentrazione di azoto iniziale è sostituita dal
suo valore disciolto in soluzione per valutare se si formino altri precipitati.
56
Modello sulla precipitazione in acciai HSLA (Particle-Size-Grouping Model)
Se entrambi i precipitati si formano le condizioni diventano le seguenti:
(1.48)
(1.49)
(1.50)
e la soluzione può essere riassunta come segue:
(a) Ad alte temperature, quando Nb0 * N0 < KNbN e Al0 * N0 < KAlN, non ci
sono precipitati.
(b) A temperature più basse, quando Nb0 * N0 > KNbN o Al0 * N0 > KAlN sono
soddisfatte:
(i)
Se Nb0 * N0 > KNbN la soluzione è data come un caso di singolo
NbN.
(ii)
Se Al0 * N0 > KAlN la soluzione è simile all’eq.(1.46), ma tutti i
valori di Nb sono rimpiazzati da i corrispondenti valori di Al.
(c) Se la temperatura diminuisce ancora al punto che Nb0 * N0 > KNbN e
Al0*N0 > KAlN sono entrambe soddisfatte, Nb0*N0 / KNbN e Al0*N0/ KAlN
sono calcolate e comparate:
(i)
Se Nb0 * N0 / KNbN è maggiore, la seguente condizione è
verificata
(1.51)
(ii)
Se vera, entrambi i precipitati si formano, in caso contrario solo il
NbN.
Se Al0 * N0/ KAlN è maggiore la prossima condizione è verificata
(1.52)
Se vera, allora si formano entrambi i precipitati, in caso contrario
solo il AlN.
57
Capitolo 1
(iii)
Se entrambi si formano,le formule sono quelle espresse in
fig.1.22.
Figura 1.22. Formule di precipitazione.
58
Modello sulla precipitazione in acciai HSLA (Particle-Size-Grouping Model)
1.4 Kinetic Model
Nel seguente paragrafo si spiegherà con maggior dettaglio come si applica il
modello cinetico [6] per la formazione di precipitati in acciai microlegati.
Il modello utilizzato per la valutazione della distribuzione delle particelle di
precipitati in funzione delle dimensioni è il PSG MODEL (Particle Size
Grouping).
L’idea principale di questa tecnica è suddividere l’intero range possibile di
particelle in gruppi, ognuno caratterizzato da una dimensione media: verrà
quindi descritto il “PSG Model”, prima quello basato sulla “collisione” delle
particelle tra loro e, successivamente, il modello creato per il fenomeno di
“diffusione”.
Nella seguente trattazione con la lettera j si indica il numero del “gruppo”, con
Vj il volume caratteristico e con rj il raggio caratteristico per ogni gruppo. A tal
proposito risulta efficace per la comprensione l’osservazione di fig.1.23.
La densità numerica per ogni gruppo j di particelle è definita dall’eq.(1.53):
(1.53)
Questa sommatoria riguarda tutte le particelle il cui volume giace tra due valori
soglia; il volume soglia che separa due gruppi vicini, ( Vj,j+1 ), è assunto come la
media geometrica dei volumi caratteristici di questi due gruppi:
(1.54)
Se la nuova particella generata ha il suo volume compreso tra Vj,j-1 e Vj,j+1 , essa
viene conteggiata nel gruppo j. L’incremento della densità numerica delle
particelle del gruppo j-esimo, viene quindi variato in accordo con la differenza
tra il volume della nuova particella e Vj, per conservare la massa.
59
Capitolo 1
Il rapporto di volumi tra due gruppi adiacenti è il seguente:
(1.55)
Figura 1.23. Schema della distribuzione di particelle nel modello PSG.
Per generare valori soglia regolarmente spaziati, Rv è di solito variato, tuttavia,
per valori di Rv costanti, i volumi caratteristici e soglia del metodo PSG possono
essere espressi come:
(1.56)
(1.57)
60
Modello sulla precipitazione in acciai HSLA (Particle-Size-Grouping Model)
Dove il volume del gruppo 1, V1, è calcolato utilizzando il volume molare della
struttura cristallina precipitata VP (m3/mol) ed dove NA è il numero di Avogadro
(6.022*1023).
(1.58)
Il numero di particelle contenute in un dato volume del modello PSG è il
seguente:
(1.59)
(1.60)
Mentre il raggio di una particella può essere espresso con l’eq.(1.61):
(1.61)
Dove Df è la dimensione frattale, che può variare tra 1 (precipitati aghiformi) e 3
(completa coalescenza in sferette). (Nel corso della trattazione Df=3).
61
Capitolo 1
Il Modello PSG per “collisione”
Applicando il metodo PSG al modello delle collisioni tra particelle, si seguono
le seguenti regole:
quando la particella del gruppo j collide con una piccola particella,
appartenente a un gruppo dall’1 al valore kc,j, allora questa rimane nel
gruppo j e aumenta la densità numerica Nj
quando una particella del gruppo j collide con un’altra particella
relativamente grande, appartenente ad un gruppo più grande di kc,j,
genera una particella nel gruppo j+1 o maggiore
quando una particella del gruppo j-1 collide con una particella
appartenete ad un gruppo compreso tra kc,j e j-1, genera una particella del
gruppo j
Combinando queste regole si realizza la seguente formula espressa nella
fig.1.24.
Figura 1.24. Formula per il modello PSG per collisione.
62
Modello sulla precipitazione in acciai HSLA (Particle-Size-Grouping Model)
Con i seguenti valori di kc,j:
(1.62)
E dove i,j è la frequenza di collisione tra una particella i e una particella j.
Infine la densità numerica del gruppo 1 nel tempo è calcolata come:
(1.63)
63
Capitolo 1
Il Modello PSG per “diffusione”
Tutte le particelle, all’interno di un gruppo j-esimo, rimangono ancora
all’interno del medesimo gruppo anche dopo eventi di crescita o dissociazione
per diffusione, eccetto per quelli definiti ”border sizes” che interessano
entrambe le ‘dimensioni soglia’ che definiscono i gruppi vicini: njL e njR.
L’eq.(1.64) è quindi quella di bilancio per questo metodo:
(1.64)
Dove
njL è la densità numerica di quelle particelle del gruppo j che cadono nel gruppo
j-1 per la perdita di una molecola,
njR è la densità numerica di quelle particelle del gruppo j che saltano nel gruppo
j+1 per l’acquisto di una molecola,
mj, mj-1,j , mj,j+1 sono il numero di molecole contenute al centro e ai confini di
ogni gruppo j,
ceil approssima il numero dato per eccesso,
floor approssima il numero dato per difetto.
64
Modello sulla precipitazione in acciai HSLA (Particle-Size-Grouping Model)
Il primo ed il secondo termine a destra dell’uguale stimano la crescita e la
dissociazione per diffusione all’interno del gruppo j, il terzo e quarto termine
stimano la crescita e la dissociazione per diffusione tra gruppi, gli ultimi due
termini quantificano la perdita delle particelle del gruppo j-esimo, per la crescita
e la dissociazione per diffusione delle particelle del gruppo j-esimo tra loro.
Le particelle contenute nel gruppo 1 sono un caso speciale perché è l’unico
gruppo che interagisce con tutti gli altri e allora il metodo PSG utilizza la
seguente equazione di bilancio per j=1:
(1.65)
I coefficienti di crescita j e dissociazione j per diffusione di un gruppo j-esimo
di particelle si ricavano dalle eq.(1.66/67).
(1.66)
(1.67)
(1.68)
65
Capitolo 1
Dove
D è il coefficiente di diffusione (m2/s),
ri è il raggio di una particella i-esima (m),
n1,eq è la densità numerica delle molecole disciolte all’equilibrio (#/m3),
è la tensione superficiale fra i precipitati e l’acciaio (J/m2),
Vp è il volume molare del precipitato (m3/mol),
R è la costante ideale dei gas (8314 J/(K*mol) ),
T è la temperatura assoluta (K).
Il raggio, i coefficienti di crescita e dissociazione per diffusione per le particelle
“border sized” si ricavano invece come segue:
(1.69)
(1.70)
(1.71)
(1.72)
(1.73)
(1.74)
66
Modello sulla precipitazione in acciai HSLA (Particle-Size-Grouping Model)
La densità numerica per i “border sizes” njL e njR sono stimati da una
progressione geometrica:
(1.75)
(1.76)
Se njL ≠ 0 e nj+1C = 0, njR viene calcolato così:
(1.77)
La densità numerica al centro di ogni gruppo j-esimo è calcolata assumendo due
progressioni geometriche all’interno di ogni gruppo:
(1.78)
(1.79)
(1.80)
67
Capitolo 1
Infine la densità numerica media per ogni gruppo viene così calcolata:
(1.81)
Quando il metodo PSG è applicato ad un processo di precipitazione reale, sono
necessari modelli addizionali per la storia delle temperature e per le
concentrazioni di massa per ogni elemento disciolto all’equilibrio.
Per una data composizione dell’acciaio ed una data evoluzione delle
temperature, il primo passo da compiere è utilizzare il “modello all’equilibrio”,
per calcolare le concentrazioni disciolte di ogni elemento ad ogni temperatura e
identificare l’elemento critico che limita il numero delle singole molecole
disponibili per formare il precipitato di interesse, come funzione del tempo.
La condizione iniziale di partenza dallo stato liquido è la completa dissoluzione
con la densità numerica delle singole molecole, N1 (t=0), uguale alla densità
numerica totale ns del precipitato di interesse.
Per una composizione contenente una concentrazione M0 dell’elemento M e una
concentrazione X0 dell’elemento X, allora ns per il precipitato MxXy è così
calcolato:
(1.82)
Dove AM e AX sono le masse atomiche degli elementi M ed X e steel è la densità
della matrice d’acciaio (circa 7500 kg/m3). Tutte le altre particelle hanno densità
numerica pari a zero.
68
Modello sulla precipitazione in acciai HSLA (Particle-Size-Grouping Model)
La densità numerica all’equilibrio delle singole molecole del precipitato
nell’acciaio, n1,eq , è calcolato a partire dalle concentrazioni della massa disciolta
all’equilibrio:
(1.83)
I coefficienti di diffusione e i tassi di dissociazione sono aggiornati per ogni
passo di tempo in accordo con l’evoluzione della temperatura. Questo modello
calcola come la distribuzione delle particelle in base alle dimensioni evolva nel
tempo.
69
Capitolo 1
70
CAPITOLO 2
Modello numerico sulla precipitazione di
microalliganti in acciai al niobio
Nel corso di questi ultimi anni, per l’importanza che rivestono gli acciai micro
legati di cui si è trattato nel capitolo precedente, molti studi sono stati effettuati
per comprendere gli effetti delle precipitazioni di niobio nella ricristallizzazione
dell’austenite durante la laminazione a caldo e durante i processi di colata e
riscaldamento, con la volontà di riuscire a prevedere la formazione dinamica dei
precipitati, compresa composizione, morfologia e distribuzione dei precipitati in
funzione delle condizioni di processo.
Di seguito, in questo capitolo, verrà descritto nei dettagli il modello che è stato
realizzato attraverso l’utilizzo di Scilab che è un programma per il calcolo
numerico finalizzato ad applicazioni scientifiche ed ingegneristiche, grazie al
quale si è riusciti a simulare la precipitazione di nanoprecipitati in acciai
microlegati al Nb e Al nel processo di colata continua che prende spunto dal
modello PSG, di cui si è trattato in precedenza, ma da cui si discosta
sensibilmente per la netta divisione tra il fenomeno di nucleazione e quello di
accrescimento.
Obiettivo della simulazione è quindi quello di prevedere:
la quantità dei precipitati ad ogni temperatura
la distribuzione dei precipitati in base alle dimensioni includendo la
transizione tra nucleazione e accrescimento
Capitolo 2
2.1 Determinazione della temperatura critica di precipitazione
Prima della realizzazione del modello vero e proprio, che permette di valutare la
distribuzione e le dimensioni dei precipitati nel tempo, in funzione della
temperatura, è necessario inizialmente realizzare un modello ausiliario in grado
di identificare quale sia la temperatura di inizio precipitazione, vale a dire la
temperatura dalla quale i precipitati iniziano a formarsi.
I passaggi che seguono, corrispondenti a questo modello e anche a quello di
precipitazione, hanno come oggetto di studio il carburo di niobio (NbC) e, di
conseguenza, i dati e le informazioni corrispondenti utilizzati nel programma, si
rifanno a questo composto, nella consapevolezza che se si fosse interessati ad
altri composti non bisognerebbe fare altro che utilizzare i rispettivi dati/valori
presenti in letteratura, senza particolari accorgimenti o difficoltà. Per l’appunto
oltre che per il carburo di niobio, il programma è stato poi messo a punto anche
per il nitruro di niobio (NbN) e per il nitruro di alluminio (AlN), altri comuni
precipitati di interesse durante i fenomeni di precipitazione.
Per il corretto utilizzo del programma bisogna conoscere:
la composizione iniziale in lega dei componenti che formano il
precipitato (come percentuale in peso)
l’andamento della temperatura in funzione del tempo
In particolare si è ipotizzato un andamento della temperatura lineare
decrescente, da 1600K a 300K, con la temperatura che diminuisce di un grado
kelvin ogni secondo, per avere una relazione tempo-temperatura relativamente
semplice e di rapida comprensione. Chiaramente essendo questo un dato in
ingresso al programma può essere variato senza difficoltà a seconda del
processo che si voglia simulare.
Definiti l’andamento della temperatura e la composizione iniziale dei
componenti si può incominciare a parlare più nello specifico del modello che
valuta la temperatura critica di precipitazione.
72
Modello numerico sulla precipitazione di microalliganti in acciai al niobio
In generale, trattando di una reazione che coinvolga un elemento di lega, M, ed
uno interstiziale, X, all'interno della matrice di austenite, si può affermare come
questa reazione porti alla formazione di un composto MxXy:
(2.1)
con x e y coefficienti stechiometrici della reazione (nel caso di studio, NbC:
x=y=1).
Il prodotto di solubilità, dipendente dalla temperatura, è definito come:
(2.2)
dove aM, aX, e aMxXy sono le attività di M, X e MxXy, rispettivamente: l'attività è
una grandezza adimensionale e rappresenta in modo esatto la
concentrazione molare di una specie chimica.
Il prodotto di solubilità negli acciai diminuisce con il diminuire della
temperatura, in questo modo si ha una determinata temperatura critica al di sotto
della quale i precipitati possono formarsi.
Conoscendo la definizione di attività si possono esplicitare i termini relativi alle
concentrazioni degli elementi:
(2.3)
Dove
rappresenta il coefficiente di attività dell’elemento M e, [M] la sua
effettiva concentrazione.
73
Capitolo 2
Nello studio dei precipitati, così come all’interno del modello che è stato
realizzato, è possibile semplificare l'espressione del prodotto di solubilità
considerando unitari i coefficienti di attività dei due elementi in modo tale che
l’espressione nell’eq. (2.2) possa essere anche scritta nel seguente modo:
(2.4)
Dalla letteratura [5] si è quindi ricercato il valore del prodotto di solubilità per
quanto concerne il composto di interesse (NbC), ricavando due espressioni di
KMX , una valida in fase e una in fase α:
(2.5)
(2.6)
Riporto per completezza i medesimi valori del prodotto di solubilità nel caso del
nitruro di niobio :
(2.7)
(2.8)
E nel caso del nitruro di alluminio:
(2.9)
74
Modello numerico sulla precipitazione di microalliganti in acciai al niobio
(2.10)
Utilizzando un opportuno ‘ciclo for’ all’interno del programma di calcolo si è
quindi riusciti a quantificare il valore dell’attività del composto (aMX) in
funzione di tempo e temperatura. I primi precipitati iniziano a formarsi nel
momento in cui si ha un’attività del composto pari all’unità, in modo che
l’espressione dell’eq.(2.4) possa essere riscritta nel seguente modo:
(2.11)
Con il programma in Scilab, valutando istante per istante il valore di aMX, si è
risaliti alla temperatura alla quale esso assume valore unitario ed essa
rappresenta la temperatura critica di precipitazione, dopo la quale i precipitati
possono formarsi.
Figura 2.1. Andamento attività NbC in funzione della temperatura e Temperatura critica.
75
Capitolo 2
Nella seguente tabella riporto i valori della temperatura critica valutati nel caso
dei tre precipitati di interesse:
Tabella 2.1. Temperature critiche di precipitazione nel caso di NbC, NbN, AlN.
Temperatura critica di precipitazione
NbC
1242 K
NbN
1382 K
AlN
1423 K
Una volta individuata la temperatura critica di precipitazione si può passare a
trattare il programma vero e proprio che si occupa del fenomeno della
nucleazione e dell’accrescimento dei precipitati.
2.2 Variazione delle concentrazioni e coefficiente di diffusione
Il passo successivo da compiere per procedere con il modello di simulazione è
quello di realizzare un altro ‘ciclo for’, questa volta per valutare l’andamento
delle concentrazioni dei due elementi (in questo caso Nb e C) all’equilibrio, al
variare della temperatura, a partire da quella di precipitazione (sopra questa
temperatura ricordo che non si formano precipitati).
Si sono sfruttate le due seguenti relazioni per valutare le concentrazioni degli
elementi all’equilibrio, all’interno della matrice metallica:
(2.12)
76
Modello numerico sulla precipitazione di microalliganti in acciai al niobio
(2.13)
I valori di interesse degli elementi oggetto dello studio sono riportati nella
seguente tabella:
Tabella 2.2. Massa atomica e concentrazioni nominali di Nb, C, Al, N.
niobio
carbonio
alluminio
azoto
Massa atomica
(g/mole)
92.91
12.01
26.98
14
% elemento in
lega
0.036
0.031
0.031
0.006
Di seguito si riporta la fig.2.2 che mostra l’andamento della concentrazione di
niobio al variare della temperatura.
77
Capitolo 2
Figura 2.2. Andamento della concentrazione di niobio con la temperatura.
In modo analogo a quanto si era fatto con il prodotto di solubilità, ora si procede
alla valutazione del coefficiente di diffusione: infatti questo processo di
precipitazione, così come accade anche per altre reazioni, si basa sul trasporto di
massa che avviene per diffusione. Con questo termine si intende il
fenomeno di trasporto di materia mediante il movimento di atomi.
Dalla letteratura [3], sono state utilizzate le seguenti espressioni per valutare il
coefficiente di diffusione (m2 / s) del Nb ed Al in fase e in fase α:
Nb:
(2.14)
(2.15)
78
Modello numerico sulla precipitazione di microalliganti in acciai al niobio
Al:
(2.16)
(2.17)
Dove R è la costante universale dei gas (8.314 J*K-1*mole-1) e T la temperatura
in gradi kelvin.
2.3 Fase di nucleazione
Eseguiti in successione gli step del modello, precedentemente elencati, si può
incominciare a trattare il fenomeno della nucleazione e di come questo sia stato
implementato all’interno del programma di calcolo.
La nucleazione è quel fenomeno per il quale in una matrice metallica compare,
al variare delle condizioni di equilibrio (per esempio durante un
raffreddamento), una particella strutturalmente stabile da cui si sviluppa una
nuova fase. Nel caso della solidificazione si ha la comparsa, in seno al metallo
liquido, di particelle solide (nuclei) che si accrescono fino al completamento
della trasformazione di stato.
I meccanismi di nucleazione possono essere sostanzialmente di due tipi: si può
avere nucleazione omogenea, che avviene all'interno dei grani della fase
metallica, oppure nucleazione eterogenea, che avviene in corrispondenza di
difetti quali dislocazioni, inclusioni e vacanze.
Nel programma si è simulato il fenomeno di nucleazione omogenea, inteso
come il fenomeno di interesse.
Nel processo di nucleazione omogenea è necessaria la presenza di un flusso di
calore uscente dal sistema verso l'ambiente esterno di entità tale da far variare le
energie libere del sistema [7].
79
Capitolo 2
In particolare la nascita di un nucleo solido stabile è possibile solo se la forza
termodinamica associata alla nucleazione di un certo volume solido è superiore
all'energia superficiale associata al medesimo nucleo.
Si può quindi andare a stabilire la variazione dell'energia libera di Gibbs
conseguente alla formazione di un nucleo solido:
(2.18)
Dove
è l’energia libera di superficie, legata alla superficie di separazione
solido-liquido, mentre
è l’energia libera di volume, legata al volume della
particella.
Assumendo quindi nuclei di geometria sferica si può esplicitare tutti i termini
precedenti:
(2.19)
Dove, all’interno dell’eq.(2.19), sono presenti i seguenti parametri:
r: raggio di nucleazione (m)
σ: energia di interfaccia tra particelle precipitate e la fase della matrice
(J/m2), nel programma questo valore è stato posto uguale a 0.5 J/m2
come da valori coerenti presenti in letteratura [5] nel caso del niobio
Lf: calore latente del precipitato di interesse (J/mole)
Tabella 2.3. Calore latente di NbC, NbN, AlN.
Calore latente (j/mole)
80
NbC
45640.2
NbN
29079.52
AlN
53274
Modello numerico sulla precipitazione di microalliganti in acciai al niobio
Vp: volume molare del precipitato di interesse (m3/mole)
Tabella 2.4. Volume molare di NbC, NbN, AlN.
Volume molare (m3/mole)
NbC
13.39*10-6
NbN
9.7*10-6
AlN
12.54*10-6
Tf: temperatura critica di precipitazione (K)
ΔTn: differenza fra la temperatura critica e quella del “processo” che
varia nel tempo
(2.20)
In natura una trasformazione è spontanea, progredisce e quindi il germe
cristallino in formazione risulta stabile, quando la sua formazione conduce ad
una riduzione di energia libera nel sistema cioè se ∆G < 0. Valutando il
contributo delle due componenti di ∆G appare evidente come ∆GS è sempre
positivo, quindi tale componente gioca sempre a sfavore della nucleazione, e
come di conseguenza per avere nuclei stabili, la componente ∆GV deve
compensare l’effetto di ∆GS, cioè ∆GV < 0 con |∆GV | > |∆GS|.
Entrambe le componenti di ∆G sono in funzione del raggio, per cui esisterà un
certo valore rc, raggio critico, che rappresenta il confine tra lo sviluppo del
nucleo solido e la sua dissoluzione. La fig. 2.3, mostra come un germe per non
essere riassorbito deve superare rc e, come per raggiungere la stabilità totale
(∆G < 0), esso debba continuare a crescere.
81
Capitolo 2
Figura 2.3. Energia libera di Gibbs in funzione del raggio di nucleazione.
Il raggio critico, essendo un punto di massimo, si ricava differenziando ∆G in
funzione del raggio e ponendo la derivata uguale a 0:
(2.21)
(2.22)
In nuclei molto piccoli prevale l’effetto di ∆GS che causa il riassorbimento dei
nuclei stessi, mentre in nuclei di dimensioni maggiori prevale l’effetto ∆GV
favorendone la progressiva aggregazione di particelle. Si ottiene così per ogni
temperatura un certo raggio critico di nucleazione rC, come risulta illustrato
nella seguente fig. 2.4:
82
Modello numerico sulla precipitazione di microalliganti in acciai al niobio
Figura 2.4. Raggio critico in funzione della temperatura per il NbC.
2.4 Fase di accrescimento
Dopo che si sono determinati i raggi di nucleazione dei nuclei solidi per ogni
temperatura, si passa a trattare il fenomeno dell’accrescimento dei suddetti
nuclei, attraverso il seguente metodo ricorsivo:
Per ogni istante di tempo (legato alla temperatura) j, si conosce il valore
del raggio critico
dove i indica l’indice di tempo che riguarda
esclusivamente il fenomeno dell’accrescimento a partire dall’istante j di
formazione del nucleo solido. Conoscendo il valore del raggio risulta
immediato il calcolo di superficie
e volume .
83
Capitolo 2
Ad ogni nucleo formato con la nucleazione, si attribuisce all’istante di
tempo successivo, un corrispondente incremento volumetrico
,
espresso dalla seguente equazione:
(2.23)
Dove Di è il coefficiente di diffusione all’istante di tempo corrispondente ad una
certa temperatura,
indica il passo di tempo e
rappresenta il gradiente di
concentrazione, dove al numeratore dCi risulta essere pari alla differenza
all’istante i tra la concentrazione iniziale in lega dell’elemento
e quella
all’equilibrio alla temperatura corrispondente
:
(2.24)
Determinato l’incremento volumetrico, questo si somma al volume del
germe solido iniziale determinando così un nuovo volume
, un
nuovo raggio
ed una nuova superficie
:
(2.25)
In questo modo si può definire ora la velocità di accrescimento per ogni
nucleo:
(2.26)
84
Modello numerico sulla precipitazione di microalliganti in acciai al niobio
E di conseguenza un nuovo gradiente di concentrazione, così calcolato:
(2.27)
Da usarsi nella formula dell’eq. (2.23), per la determinazione dell’incremento
volumetrico dell’istante successivo sempre facendo riferimento al nucleo
originato dal raggio critico j corrispondente.
Per chiarezza si riporta di seguito il diagramma di flusso del programma.
Figura 2.5. Diagramma di flusso dell’accrescimento.
85
Capitolo 2
Assumendo come esempio che si voglia passare con il programma da una
temperatura di 1241K a 300K con una diminuzione di temperatura di un grado
al secondo, occorrono allora 941 secondi di processo e, di conseguenza, il ‘ciclo
for’ avrà come estremi 1 e 942 con passo 1.
Avendo in questo caso specifico una temperatura diversa ogni istante, il risultato
sarà l’ottenimento di una matrice triangolare inferiore di 941 righe e 941
colonne dove le righe sono gli istanti di tempo e le colonne rappresentano i
diversi “gruppi” di nuclei che enucleano a temperature diverse e che poi
accrescono.
Riporto di seguito un piccolo estratto dell’esempio citato quando la temperatura
che passa da 900K a 895K nel caso del NbC:
Figura 2.6. Nucleazione ed accrescimento da 900K a 895K nel caso del NbC.
86
Modello numerico sulla precipitazione di microalliganti in acciai al niobio
2.5 Valutazione della densità numerica dei precipitati nel tempo
Ottenuti, prima i raggi di nucleazione e poi quelli rispettivi di accrescimento dei
nuclei solidi che si sono formati, il passaggio successivo del programma prevede
la sostituzione dei valori dei raggi di nucleazione all’interno dell’eq.(2.19) [7]
per identificare il valore della variazione dell’energia libera di Gibbs per ogni
raggio, che deve poi essere utilizzata all’interno della seguente eq.(2.28) per
calcolare il numero di particelle precipitate per ogni istante di tempo Nn
partendo dai siti di nucleazione N0 (precipitati/m2), di cui tratteremo di seguito:
(2.28)
Dove kb è la costante di Boltzmann e indica il rapporto fra la costante universale
dei gas e il numero di Avogadro inteso come numero di particelle contenute in
una mole (6.022*1023):
(2.29)
Il cui valore è pari a 1.3806488*10-23 J/K.
Concentrando ora l’attenzione sul valore di N0, esso rappresenta il numero di siti
di nucleazione da cui poi si sviluppano le Nn particelle (precipitati/m2) ricavate
con l’eq. (2.28).
Per trovare il numero di siti è necessario ricavare una funzione dipendente dalla
superficie totale di nucleazione, a sua volta proporzionale all’ottaedro troncato
di Kelvin: quest’ultimo in geometria è ottenuto troncando le cuspidi
dell'ottaedro regolare: ha 14 facce regolari e dei suoi 36 spigoli 24 separano una
faccia esagonale da una quadrata e 12 separano due facce esagonali come
illustrato dalla seguente fig.2.7.
87
Capitolo 2
Figura 2.7. Ottaedro troncato e suo sviluppo nel piano.
Lo studio sulle proprietà dell’ottaedro troncato lo si deve al fisico britannico
Lord Kelvin [8], che nel 1887 investigò su quale fosse il modo più efficiente per
ripartire lo spazio in celle di uguale volume (come accade per le bolle di sapone)
con la più piccola area a dividerle.
La soluzione fu per l’appunto un alveare di ottaedri troncati e questa
approssimazione è la medesima che si utilizza nel programma per valutare i
grani solidi in formazione nei siti di nucleazione.
Figura 2.8. Alveare di ottaedri troncati.
88
Modello numerico sulla precipitazione di microalliganti in acciai al niobio
Partendo da plausibili valori del raggio della sfera circoscritta all’ottaedro
troncato (es. 4-6μm) si procede con la determinazione dello spigolo a , della
superficie S e del volume V dell’ottaedro troncato attraverso le seguenti
espressioni, ricavabili in letteratura [9]:
(2.30)
(2.31)
(2.32)
Conoscendo il volume di un ottaedro si può ricavare il numero di ottaedri
contenuti in 1m3 di volume:
(2.33)
E la superficie totale di nucleazione (m2):
(2.34)
Dove 12 sono gli spigoli che separano due facce esagonali. Ricavata la
superficie totale di nucleazione, per valutare quanti siti di nucleazione ci
possono essere al suo interno si utilizza la distanza tra i nuclei, interpretandola
come il raggio di un cerchio, che rappresenta lo spazio di interazione del singolo
germe solido in formazione con quelli vicini (Superficie gradiente).
89
Capitolo 2
Figura 2.9. Esempio semplificativo del numero siti nella superficie totale di nucleazione.
Concludendo, il numero di siti di nucleazione sarà dato dalla seguente
espressione:
(2.35)
Per terminare la descrizione del modello non rimane che esaminare la modalità
con la quale si valutano le distanze tra i precipitati:
Si valuta innanzitutto la sommatoria degli Nn istante per istante e la si
utilizza per ricavare la distanza l tra i precipitati che rappresenta la
distanza alla quale interagiscono i campi di distribuzione dei soluti:
(2.36)
90
Modello numerico sulla precipitazione di microalliganti in acciai al niobio
Contemporaneamente si valuta il valore della distanza critica
,
vale a dire la distanza al di sotto della quale c’è interazione tra due o più
precipitati e che è data dalla seguente eq.(2.37):
(2.37)
Con tutti i valori che fanno riferimento al nucleo appena formatosi
Se la distanza è inferiore alla distanza critica, <
,allora c’è una
variazione della concentrazione in lega dell’elemento M che sarà data
dalla nuova espressione:
(2.38)
In caso contrario la concentrazione rimane la medesima dello step
precedente.
Di seguito riporto i grafici più significativi ricavati dall’utilizzo del
programma, sottolineando che, a parità di grafico, gli andamenti per i tre
precipitati di interesse (NbC, NbN, AlN) sono i medesimi.
91
Capitolo 2
Figura 2.10. Andamento N n in funzione dei raggi di nucleazione per NbC.
Nella fig.2.10 si mostra l’andamento degli Nn (precipitati/m2) in funzione del
raggio di nucleazione, vale a dire si mostra il numero di precipitati associati ad
un valore specifico del raggio di nucleazione: la forma del grafico ricorda una
semi parabola con la concavità verso il basso e il cui vertice rappresenta i
massimi valori di Nn che si legano a “bassi” valori dei raggi di nucleazione,
ossia 4-5*10-10m.
Medesimo andamento si riconosce nella fig.2.11 in cui si mostra l’andamento
degli Nn in funzione della temperatura per il NbN, con i valori massimi che si
raggiungono a basse temperature, ovvero a 400K.
92
Modello numerico sulla precipitazione di microalliganti in acciai al niobio
Figura 2.11. Andamento N n in funzione della temperatura per il NbN.
Nella fig.2.12 viene mostrato invece l’andamento delle frazioni di superficie
totali dei precipitati in funzione della temperatura.
Ovvero si moltiplica i singoli valori di Nn per l’area della sfera corrispondente
utilizzando il raggio di nucleazione associato al valore di Nn come espresso
dall’eq.(2.39).
(2.39)
93
Capitolo 2
Figura 2.12. Andamento frazioni superficie totali in funzione della temperatura per il NbC.
Dall’analisi di questo grafico è evidente come alla alte temperatura il valore
della frazione di superficie risulti inferiore all’unità con un picco di valori che
viene raggiunto in un intervallo di temperature tra gli 800K-850K.
94
CAPITOLO 3
Analisi sperimentale e confronto con il
modello di simulazione
Lo scopo della presente tesi è stato quello di realizzare un modello previsionale
per la formazione di precipitati quali carburi/nitruri di niobio, durante il
processo di colata continua di bramme in acciaio microlegato con niobio.
Avendo descritto nel capitolo precedente quali siano stati i passi che hanno
permesso di realizzare il modello, in questo capitolo ci si concentra sulla
validazione del modello, confrontando i risultati dello stesso con quelli derivanti
da una campagna sperimentale, al fine di valutare in particolare l’esattezza del
programma previsionale realizzato, in termini di:
Distanza tra precipitati
Frazione di superficie occupata dai precipitati
Numerosità dei precipitati
Per la campagna sperimentale si sono utilizzati sostanzialmente due tipi di
provini, che chiameremo “Dillinger” e “Voestalpine”, dal nome delle acciaierie
di provenienza (acciaieria Dillinger situata a Dillingen (Germania) ed acciaieria
Voestalpine situata a Linz (Austria)).
Capitolo 3
La composizione chimica dei provini forniti dall'acciaieria Dillinger è quella
riportata in tabella 3.1.
Tabella 3.1. Composizione chimica (in % in peso) dei provini forniti dall'acciaieria
Dillinger.
C
0,17
Si
0,29
Mn
1,29
Cr
0,32
Mo
0,27
Nb
0,029
Ti
0,0027
N
0,0066
Al
0,068
La composizione chimica dei provini Voestalpine è invece riportata in tabella
3.2.
Tabella 3.2. Composizione chimica (in % in peso) dei provini forniti dall'acciaieria
Voestalpine. Boro e azoto sono dati in ppm.
C
0,174
Mo
0,006
Si
0,387
Cu
0,15
Mn
1,14
V
0,006
P
0,0091
Nb
0,022
S
0,0006
Ti
0,002
B
2
Cr
0,178
N
43
Ni
0,27
Al
0,04
Nella simulazione della colata continua si sono fatte alcune semplificazioni:
scendendo lungo la zona di raffreddamento secondario si ha il continuo
alternarsi di zone di contatto della pelle della bramma con i rulli, a zone di non
contatto. Il tempo di non contatto è in generale molto maggiore del tempo di
contatto, al punto che si è ragionevolmente trascurato l'entità del secondo
rispetto a quello del primo.
Si è considerato così istantaneo il tempo di contatto e assumendo che il tempo di
non contatto coincida con quello necessario alla bramma per percorrere
l'interasse verticale tra i rulli.
Le tipologie di provini utilizzati, insieme con velocità di colata e numero di
contatti con rulli sono riassunti nella tabella 3.3.
96
Analisi sperimentale e confronto con il modello di simulazione
Tabella 3.3. Piano delle prove sperimentali.
number
1
2
3
4
5
6
7
8
9
10
11
12
13
material
voestalpine
voestalpine
voestalpine
voestalpine
voestalpine
voestalpine
voestalpine
voestalpine
dillinger
dillinger
dillinger
dillinger
dillinger
vel [m/min]
0,75
0,5
0,4
0,3
0,5
0,75
0,4
0,3
0,75
0,75
0,5
0,4
0,3
kind of test
9 contacts
9 contacts
9 contacts
9 contacts
3 contacts
3 contacts
3 contacts
3 contacts
9 contacts
3 contacts
3 contacts
3 contacts
3 contacts
Il ciclo termico imposto ai provini durante la generica prova di secondary
cooling con l'effetto dei rulli è qualitativamente rappresentato in fig.3.1.
Figura 3.1. Ciclo termico imposto alla parte centrale del provino durante la simulazione
del secondary cooling con contatto dei rulli. A) riscaldamento iniziale; B) mantenimento di
omogeneizzazione; C) simulazione di secondary cooling con contatto dei rulli;D) brusco
raffreddamento.
97
Capitolo 3
L'andamento delle temperature che si è cercato di mantenere nella simulazione
nelle tipologie di colata è riportato in Tabella 3.4.
Tabella 3.4. Temperature e tempi adottati durante la simulazione delle modalità di colata.
Temperature
Provino
(s)
1250
1200
1100
1200
1150
1050
1150
1100
1000
1100
1050
950
1050
1000
900
1000
950
850
950
900
800
900
850
750
850
800
98
0,75 m/min (s)
0
6
10
24
30
34
48
54
58
71
77
81
95
101
105
119
125
129
142
148
152
166
172
176
190
196
0,5 m/min (s) 0,4 m/min (s)
0
6
10
44
50
54
88
94
98
132
138
142
176
182
186
220
226
230
264
270
274
308
314
318
352
358
0
6
10
54
60
64
108
114
118
162
168
172
216
222
226
270
276
280
324
330
334
378
384
388
432
438
0,3 m/min
(s)
0
6
10
69
75
79
138
144
148
207
213
217
276
282
286
345
351
355
414
420
424
483
489
493
552
558
Analisi sperimentale e confronto con il modello di simulazione
Come si può notare dall’analisi dei dati riportati in tabella 3.4 le diverse velocità
di colata sono state convertite in un andamento della temperatura, a cui sono
stati sottoposti i provini, variata nel tempo. Concentrando ad esempio
l’attenzione sul valore di 800°C si può osservare come questa temperatura sia
raggiunta in 196 secondi con una velocità di 0,75 m/min, mentre in 558 secondi
con una velocità di 0,3 m/min, prendendo in considerazione le due velocità
estreme. Senza dilungarsi eccessivamente sulla fase sperimentale si può
riassumere come la colata continua sia stata quindi simulata tramite l’utilizzo di
opportuni provini, opportunamente riscaldati e raffreddati seguendo il ciclo
termico proposto in tabella 3.4. per le diverse velocità di colata.
A valle della simulazione del secondary cooling i provini Dillinger e
Voestalpine sono stati rotti per poi essere analizzati tramite FEG-SEM (field
emission gun scanning electron microscope).
Analisi dei precipitati mediante FEG-SEM
I provini sono stati analizzati al microscopio elettronico ad alti ingrandimenti
FEG-SEM.
Tramite esso sono state acquisite diverse immagini della superficie di frattura. I
risultati ottenuti sono osservabili qualitativamente tenendo conto delle
dimensioni dei precipitati nelle diverse acquisizioni.
Di seguito verranno proposte le immagini più caratteristiche delle superfici di
frattura con in evidenza i diversi precipitati.
Per ogni tipologia di prova sperimentale sono state effettuate a valle 30
misurazioni riguardanti le distanze tra i precipitati, osservabili dalle immagini,
ricavando per ogni prova valori di media, scarto quadratico medio e varianza.
99
Capitolo 3
1) Voestalpine - 0,75 m/min - 9 contatti
Figura 3.2. Immagine al FEG-SEM con ingrandimento a 20.000x per la superficie di
frattura del provino 1.
Nell’immagine di fig.3.2 i precipitati corrispondenti al NbC, paiono simili a
delle piccole sfere, il che corrisponde con l’assunzione teorica fatta durante
questo lavoro, ed oltre ai precipitati, le cui distanze tra loro sono riportate nella
tabella sottostante, sono ben visibili i possibili siti di nucleazione, della forma
del caratteristico ottaedro troncato, che in questa foto risultano visti in sezione.
Tabella 3.5. Distanze tra precipitati provino 1.
0,210
0,135
0,277
0,241
0,328
0,227
100
Distanze in micrometri
0,307
0,599
0,244
0,450
0,907
0,257
0,404
0,722
0,235
0,180
0,672
0,308
0,330
0,893
0,378
0,496
0,422
0,543
0,811
0,961
0,500
0,519
0,513
0,662
Analisi sperimentale e confronto con il modello di simulazione
Tabella 3.6. Media, σ, σ2 provino 1.Valori in micrometri.
Media
σ
σ2
0,457
0,232
0,053
2) Voestalpine - 0,5 m/min - 9 contatti
Figura 3.3. Immagine al FEG-SEM con ingrandimento a 20.000x per la superficie di
frattura del provino 2.
In quest’altra fig.3.3 rispetto alla fig.3.2 si notano invece dei precipitati non più
chiari e sferici come in precedenza ma si può apprezzare la presenza di clusters,
ovvero di piccoli agglomerati di precipitati che si sono formati per la vicinanza
degli stesse particelle tra loro.
101
Capitolo 3
Tabella 3.7. Distanze tra precipitati provino 2.
1,058
0,984
1,485
2,011
0,840
1,433
Distanze in micrometri
1,204
1,781
1,285
1,196
2,256
1,389
0,982
1,481
0,824
1,684
1,037
1,369
1,180
1,581
1,322
1,274
1,652
2,430
2,419
1,370
1,778
1,604
1,274
1,448
Tabella 3.8. Media, σ, σ2 provino 2.Valori in micrometri.
Media
σ
σ2
1,454
0,417
0,174
3) Voestalpine - 0,4 m/min - 9 contatti
Figura 3.4. Immagine al FEG-SEM con ingrandimento a 80.000x per la superficie di
frattura del provino 3.
102
Analisi sperimentale e confronto con il modello di simulazione
Tabella 3.9. Distanze tra precipitati provino 3.
0,252
0,208
0,228
0,245
0,188
0,258
Distanze in micrometri
0,208
0,190
0,242
0,267
0,379
0,333
0,259
0,315
0,276
0,237
0,397
0,303
0,285
0,373
0,253
0,292
0,348
0,444
0,377
0,381
0,242
0,296
0,378
0,357
Tabella 3.10. Media, σ, σ2 provino 3.Valori in micrometri.
Media
σ
σ2
0,293
0,068
0,004
4) Voestalpine - 0,3 m/min - 9 contatti
Figura 3.5. Immagine al FEG-SEM con ingrandimento a 10.000x per la superficie di
frattura del provino 4.
103
Capitolo 3
Tabella 3.11. Distanze tra precipitati provino 4.
0,221
0,160
0,143
0,142
0,100
0,146
Distanze in micrometri
0,138
1,078
0,116
0,182
0,793
0,161
0,136
0,630
0,182
0,151
0,656
0,148
0,128
0,707
0,596
1,100
0,896
0,519
0,793
0,681
0,852
0,807
1,019
0,711
Tabella 3.12. Media, σ, σ2 provino 4.Valori in micrometri.
Media
σ
σ2
0,469
0,347
0,120
5) Voestalpine - 0,5 m/min - 3 contatti
Figura 3.6. Immagine al FEG-SEM con ingrandimento a 200.000x per la superficie di
frattura del provino 5.
104
Analisi sperimentale e confronto con il modello di simulazione
Da questa fig.3.6 i precipitati non appaiono immediatamente riconoscibili ma
comunque sono identificabili con le sferette di un colore più chiaro.
Tabella 3.13. Distanze tra precipitati provino 5.
0,123
0,076
0,101
0,103
0,112
0,091
Distanze in micrometri
0,089
0,751
0,129
0,129
0,765
0,091
0,092
0,604
0,082
0,101
0,365
0,114
0,102
0,562
0,636
0,709
0,635
0,749
0,660
0,731
0,727
0,436
0,656
0,720
Tabella 3.14. Media, σ, σ2 provino 5.Valori in micrometri.
Media
σ
σ2
0,374
0,288
0,083
105
Capitolo 3
6)Voestalpine - 0,75 m/min - 3 contatti
Figura 3.7. Immagine al FEG-SEM con ingrandimento a 50.000x per la superficie di
frattura del provino 6.
Anche nella fig.3.7. dei semplici precipitati si alternano ai cluster e appaiono
entrambi di colore bianco sullo sfondo nero che invece rappresenta la matrice di
acciaio.
Tabella 3.15. Distanze tra precipitati provino 6.
1,027
0,519
1,379
0,744
1,395
1,074
106
Distanze in micrometri
0,770
0,686
0,917
0,609
0,750
0,702
0,680
0,412
0,705
0,691
0,658
0,556
0,904
1,025
0,815
0,704
0,603
0,615
0,670
0,744
0,558
0,697
0,702
0,760
Analisi sperimentale e confronto con il modello di simulazione
Tabella 3.16. Media, σ, σ2 provino 6.Valori in micrometri.
Media
σ
σ2
0,769
0,224
0,050
7)Voestalpine - 0,4 m/min - 3 contatti
Figura 3.8. Immagine al FEG-SEM con ingrandimento a 30.000x per la superficie di
frattura del provino.
Tabella 3.17. Distanze tra precipitati provino 7.
0,741
0,778
0,989
0,952
1,136
0,528
Distanze in micrometri
1,097
0,890
1,075
0,610
1,020
0,617
0,754
0,885
0,542
0,839
0,604
0,867
0,983
0,764
0,744
0,852
0,631
0,890
0,846
0,890
1,009
0,940
0,771
1,038
107
Capitolo 3
Tabella 3.18. Media, σ, σ2 provino 7. Valori in micrometri.
Media
σ
σ2
0,842
0,167
0,028
8) Voestalpine - 0,3 m/min - 3 contatti
Figura 3.9. Immagine al FEG-SEM con ingrandimento a 120.000x per la superficie di
frattura del provino 8.
Tabella 3.19. Distanze tra precipitati provino 8.
0,221
0,130
0,180
0,132
0,116
0,191
108
Distanze in micrometri
0,185
0,122
0,140
0,190
0,106
0,161
0,127
0,098
0,167
0,147
0,101
0,152
0,182
0,098
0,085
0,098
0,095
0,108
0,110
0,097
0,126
0,109
0,141
0,104
Analisi sperimentale e confronto con il modello di simulazione
Tabella 3.20. Media, σ, σ2 provino 8.Valori in micrometri.
Media
σ
σ2
0,133
0,036
0,001
9)Dillinger - 0,75 m/min - 9 contatti
Figura 3.10. Immagine al FEG-SEM con ingrandimento a 200.000x per la superficie di
frattura del provino 9.
Tabella 3.21. Distanze tra precipitati provino 9.
0,280
0,305
0,306
0,264
0,161
0,317
Distanze in micrometri
0,385
0,270
0,304
0,358
0,266
0,264
0,218
0,323
0,372
0,290
0,328
0,307
0,171
0,231
0,283
0,236
0,174
0,184
0,286
0,226
0,211
0,202
0,318
0,335
109
Capitolo 3
Tabella 3.22. Media, σ, σ2 provino 9.Valori in micrometri.
Media
σ
σ2
0,272
0,060
0,003
10) Dillinger - 0,75 m/min - 3 contatti
Figura 3.11. Immagine al FEG-SEM con ingrandimento a 50.000x per la superficie di
frattura del provino 10.
Tabella 3.23. Distanze tra precipitati provino 10.
0,610
0,506
0,341
0,268
0,214
0,361
110
Distanze in micrometri
0,716
0,906
0,490
0,682
0,741
0,498
0,549
0,662
0,417
0,407
0,943
0,336
0,463
0,549
0,971
0,668
0,522
0,731
0,701
0,950
0,890
0,426
0,643
0,670
Analisi sperimentale e confronto con il modello di simulazione
Tabella 3.24. Media, σ, σ2 provino 10.Valori in micrometri.
Media
σ
σ2
0,594
0,207
0,043
11) Dillinger - 0,5 m/min - 3 contatti
Figura 3.12. Immagine al FEG-SEM con ingrandimento a 100.000x per la superficie di
frattura del provino 11.
Tabella 3.25. Distanze tra precipitati provino 11.
0,232
0,223
0,224
0,230
0,189
0,234
Distanze in micrometri
0,326
0,101
0,299
0,133
0,109
0,280
0,163
0,117
0,244
0,207
0,133
0,220
0,156
0,094
0,087
0,117
0,120
0,134
0,094
0,116
0,106
0,103
0,106
0,096
111
Capitolo 3
Tabella 3.26. Media, σ, σ2 provino 11.Valori in micrometri.
Media
σ
σ2
0,166
0,069
0,004
12) Dillinger - 0,4 m/min - 3 contatti
Figura 3.13. Immagine al FEG-SEM con ingrandimento a 10.000x per la superficie di
frattura del provino 12.
Tabella 3.27. Distanze tra precipitati provino 12.
0,187
0,207
0,443
0,231
0,463
0,371
112
Distanze in micrometri
0,948
1,078
0,351
0,678
0,985
0,796
0,511
1,267
0,678
0,482
1,574
0,704
0,456
0,807
1,993
0,811
1,233
1,122
1,496
0,804
1,519
1,378
1,233
1,407
Analisi sperimentale e confronto con il modello di simulazione
Tabella 3.28. Media, σ, σ2 provino 12.Valori in micrometri.
Media
σ
σ2
0,873
0,470
0,221
13) Dillinger - 0,3 m/min - 3 contatti
Figura 3.14. Immagine al FEG-SEM con ingrandimento a 150.000x per la superficie di
frattura del provino 13.
Tabella 3.29. Distanze tra precipitati provino 13.
0,112
0,108
0,108
0,078
0,162
0,062
Distanze in micrometri
0,135
0,356
0,134
0,118
0,443
0,098
0,079
0,283
0,174
0,137
0,499
0,144
0,105
0,286
0,468
0,314
0,373
0,211
0,371
0,572
0,390
0,353
0,431
0,303
113
Capitolo 3
Tabella 3.30. Media, σ, σ2 provino 13.Valori in micrometri.
Media
σ
σ2
0,246
0,149
0,022
Figura 3.15. Distanze tra precipitati calcolate con il modello previsionale.
Dalla fig.3.15 si possono valutare qualitativamente e anche in modo quantitativo
l’andamento che hanno le distanze tra precipitati, utilizzando il modello
previsionale realizzato e descritto nel capitolo precedente.
In particolare emerge come i risultati sperimentali riguardanti i valori medi di
distanze tra precipitati, che si aggirano nell’intorno del micron, cioè 10-6 metri,
con ovviamente un certo intervallo di tolleranza, sono quelli che si vengono a
realizzare nei processi tra una temperatura di circa 940K a 1100/1110K.
114
Analisi sperimentale e confronto con il modello di simulazione
Una volta valutate le distanze tra precipitati, confrontandole con quelle del
modello previsionale, si è proceduto, utilizzando sempre le medesime immagini
dei provini utilizzati, con il calcolo della numerosità dei precipitati per ogni
prova e in ultima analisi con i confronti tra i valori di frazione di superficie
calcolati con il modello previsionale e quelli ricavati sperimentalmente.
Per quanto concerne la dimensione dei precipitati il parametro utilizzato come
riferimento è stato la frazione di superficie percentuale di precipitati
riscontrabile nella superficie di frattura ed osservabile su ciascuna immagine,
calcolabile come:
(3.1)
nella quale Atot,prec rappresenta la somma di tutte le aree dei precipitati mentre
Atot l'area totale di ogni immagine acquisita.
I valori di numerosità Nn e frazione di superficie sono quelli riportati in tabella
3.31.
Tabella 3.31. Valori sperimentali di frazione di superficie e numerosità su tutti i provini
utilizzati.
provino
1
2
3
4
5
6
7
8
9
10
11
12
13
frazione superficie
percentuale
0,016544
0,035536
0,015622
0,027083
0,021373
0,020163
0,013988
0,007213
0,024841
0,028518
0,060003
0,047776
0,063895
Numerosità Nn [precipitati/m^2]
3,27E+13
1,02E+13
8,18E+12
7,00E+12
1,08E+13
1,09E+13
1,15E+13
2,47E+13
2,57E+13
3,50E+13
8,30E+13
8,61E+12
3,90E+13
115
Capitolo 3
Concentrando l’attenzione inizialmente sui valori di numerosità ed in particolare
su quelli dei primi 4 provini (voestalpine) si nota in modo evidente come, con il
diminuire della velocità di colata (passando da 0,75 m/min con il provino 1 a 0,3
m/min con il provino 4), ci sia anche una diminuzione della numerosità di
precipitati riscontrati nelle immagini dei medesimi provini.
Nelle fig.3.16 e 3.17 riporto per l’appunto i casi estremi riguardanti il provino 1
ed il provino 4, valutando il valore di numerosità in funzione della temperatura
alla quale si è generato, calcolato attraverso il modello previsionale adottato.
Figura 3.16. Numerosità Nn precipitati nel provino 1 (voestalpine-0,75 m/min-9 contatti) in
funzione della temperatura.
Il valore di numerosità valutato sperimentalmente pari a 3.2798*1013 risulta
compatibile con i valori calcolati attraverso il modello previsionale ed in
particolare, appare come questo valore sia associato nel modello ad una
temperatura di circa 1120K.
116
Analisi sperimentale e confronto con il modello di simulazione
Figura 3.17. Numerosità Nn precipitati nel provino 4 (voestalpine-0,3 m/min-9 contatti) in
funzione della temperatura.
Per quanto concerne viceversa il valore di numerosità rilevato per il provino 4
pari a 7.0051*1012, anch’esso risulta compatibile con i valori del modello e
associato però ad una temperatura che si aggira intorno ai 1130K.
Prima di passare ad esaminare il comportamento del modello anche nel caso dei
provini Dillinger, risulta interessante associare i valori di numerosità citati in
precedenza per i provini 1 e 4 (che risultano essere i più rappresentativi), non
più in funzione della temperatura bensì in funzione dei raggi di nucleazione.
Questo “legame” risulterà fondamentale successivamente per il calcolo delle
frazioni di superficie.
Nelle fig.3.18 e 3.19 viene mostrato il legame tra la numerosità dei precipitati e i
valori dei raggi di nucleazione corrispondenti.
117
Capitolo 3
Figura 3.18. Numerosità Nn precipitati nel provino 1 (voestalpine-0,75 m/min-9 contatti) in
funzione dei raggi di nucleazione.
Nel caso del provino 1 il valore Nn di numerosità dei precipitati è associato ad
un valore del raggio di nucleazione pari all’incirca a 3*10-9 m. Più in generale si
può apprezzare come l’andamento sia simile a quello in funzione della
temperatura ma più netto e simile ad una retta. Questo come anche altri valori di
raggi di nucleazione risulteranno fondamentali per il calcolo della frazione di
superficie e confrontati con i valori espressi dal modello confermeranno la bontà
dello stesso.
Nella figura 3.19 è presentato il caso invece del provino 4, il cui valore di
numerosità è associato ad un valore di raggio di nucleazione pari a 3.2*10-9 m,
ovvero poco più grande del caso del provino 1.
118
Analisi sperimentale e confronto con il modello di simulazione
Figura 3.19. Numerosità Nn precipitati nel provino 4 (voestalpine-0,3 m/min-9 contatti) in
funzione dei raggi di nucleazione.
Passiamo ora ad esaminare i valori di numerosità di precipitati, confrontati con i
valori del modello previsionale, nel caso dei provini Dillinger.
In particolare alla luce dei risultati sperimentali, appare interessante soffermarci
sui valori riscontrati nei casi dei provini 9-10-11.
Nel caso del provino 9 (Dillinger-0,75 m/min-9contatti), il valore di numerosità
appare similare a quello riscontrato nel caso analogo del provino Voestalpine
(provino 1) con un valore cioè di 2.579*1013 (precipitati/m2).
A parità di tipo di provino e di velocità di colata, ma cambiando il numero di
contatti da 9 a 3, come nel caso del provino 10, il valore di numerosità aumenta
arrivando a 3.5092*1013, associato ad un valore di temperatura di circa 1120K
come si nota dalla fig.3.20.
119
Capitolo 3
Figura 3.20. Numerosità Nn precipitati nel provino 10 (dillinger-0,75 m/min-3 contatti) in
funzione della temperatura.
Valutando ora il valore di numerosità del provino 11 si può notare un’anomalia
rispetto ai casi dei provini Voestalpine, dove diminuendo la velocità di colata
diminuiva anche il valore di Nn, mentre in questo caso aumenta sensibilmente il
valore di Nn imputando questo all’interazione tra i fattori “velocità di colata” e
“numero di contatti”, come si può notare dalla fig.3.21 in cui il valore di Nn del
provino 11 è di 8.3058*1013 associato ad un valore di temperatura inferiore ai
1120K di prima, tuttavia entrambi numeri compatibili con quelli del modello
previsionale.
120
Analisi sperimentale e confronto con il modello di simulazione
Figura 3.21. Numerosità Nn precipitati nel provino 11 (dillinger-0,5 m/min-3 contatti) in
funzione della temperatura.
Risulta evidente come aumentando il valore di numerosità esso viene ad
associarsi con un valore inferiore di raggio di nucleazione, come appare ovvio
dall’andamento degli Nn, e nel caso in esame del provino 11 il raggio
corrispondente risulta essere all’incirca 2.875*10-9 m. (Fig.3.22)
121
Capitolo 3
Figura 3.22. Numerosità Nn precipitati nel provino 11 (dillinger-0,5 m/min-3 contatti) in
funzione dei raggi di nucleazione.
Esaminati i valori sperimentali di numerosità dei precipitati Nn e confrontati con
quelli possibili calcolati con il modello previsionale, si passa ora ad esaminare i
valori di frazione di superficie, effettuando il medesimo confronto per testare la
bontà del modello.
Questo passaggio risulta ancora più efficace del precedente per provare
l’esattezza del modello, in quanto ad un valore di numerosità Nn ricavato
sperimentalmente si associa un solo valore (o comunque una serie di valori
vicini e simili) di raggio di nucleazione e temperatura di precipitazione ricavati
esclusivamente dal modello previsionale.
Come anche già espresso nel capitolo precedente riguardante il modello
adottato, si moltiplica il singolo valore di Nn per l’area di una sfera che
rappresenta idealmente l’area del precipitato, utilizzando il raggio di
nucleazione corrispondente ricavato dal modello, ottenendo i valori di frazione
122
Analisi sperimentale e confronto con il modello di simulazione
di superficie (eq.3.3) che possono poi eventualmente essere confrontati non solo
in funzione dei raggi di nucleazione ma anche in funzione della temperatura
verificando se i valori calcolati con il modello sono compatibili con quelli
ricavati sperimentalmente.
(3.3)
Figura 3.23. Frazione di superficie provini voestalpine (provini 1-2-3-4-8) in funzione dei
raggi di nucleazione.
123
Capitolo 3
Nella fig.3.23 la zona evidenziata in verde rappresenta i valori di frazioni di
superficie che sono stati misurati sperimentalmente e che sono stati messi in
funzione dei raggi di nucleazione: appare così evidente come le frazioni di
superficie risultino compatibili con valori di raggio compresi tra 2.6*10-9 e
2.9*10-9 m. Tali valori di frazione di superficie vengono richiamati nella tabella
3.32.
Tabella 3.32. Frazioni di superficie per provini 1-2-3-4-8.
provino
1
2
3
4
8
frazione superficie
0,016544
0,035536
0,015622
0,027083
0,007213
Per la precisione il modello sottostima leggermente i valori di frazione di
superficie, poiché per valori di raggio di 3*10-9 dovrebbe corrispondere un
valore compreso tra 10-2 e 10-3. Tenendo conto però della differenza veramente
minima unita al fatto che si parli di grandezze minori del nanometro (che
possono portare ad errori di misurazione anche in fase sperimentale), i risultati
del modello previsionale si possono considerare soddisfacenti e del tutto
compatibili con quelli sperimentali.
Nella fig.3.24 si nota invece l’andamento dei valori di frazione di superficie in
funzione della temperatura nel caso sempre dei provini Voestalpine(1-2-3-4-8).
124
Analisi sperimentale e confronto con il modello di simulazione
Figura 3.24. Frazione di superficie provini voestalpine (provini 1-2-3-4-8) in funzione della
temperatura.
Nel caso dei provini Dillinger, si ha lo stesso comportamento dei provini
Voestalpine in cui la corrispondenza tra i valori misurati e quelli ricavabili dal
modello di frazione di superficie sono comparabili tra loro con quelli derivanti
dal modello che leggermente sottostimano quelli sperimentali come si nota dalle
fig.3.25 e 3.26.
125
Capitolo 3
Figura 3.25. Fraz. Sup. provini dillinger (provini 9-10-11) in funzione dei raggi.
Figura 3.26. Fraz. Sup. provini dillinger (provini 9-10.11) in funzione della temperatura.
126
Analisi sperimentale e confronto con il modello di simulazione
Alla luce dei risultati illustrati fino ad ora e per rendere in modo più evidente la
corrispondenza tra i valori misurati sperimentalmente e quelli calcolati tramite il
modello previsionale, seguono adesso una serie di grafici che mettono proprio in
relazione quelle che sono le grandezze di interesse di questo studio, con
l’intenzione di validare lo stesso modello realizzato.
Da una prima analisi dei risultati, emerge come ci sia una corrispondenza di
valori (numerosità, frazione di superficie e distanza tra precipitati) per quanto
riguarda i valori misurati e quelli calcolati, in un range di temperature che varia
all’incirca tra i 1130K e i 1110K.
Avendo focalizzato l’attenzione su questo intervallo di temperature, i grafici che
seguono pongono l’attenzione sulla compatibilità tra risultati sperimentali e
analitici.
Valori calcolati
Valori sperimentali misurati
5E+13
4,5E+13
4E+13
3,5E+13
3E+13
2,5E+13
2E+13
1,5E+13
1E+13
5E+12
0
0
2E+13
4E+13
6E+13
Numerosità Voestalpine[1129K-1116K]
Figura3.27. Confronto tra risultati sperimentali e analitici del modello previsionale, in
termini di numerosità di precipitati al m2, per un range di temperatura di [1129K-1116K]
per i provini Voestalpine.
127
Capitolo 3
Valori calcolati
Valori sperimentali misurati
9E+13
8E+13
7E+13
6E+13
5E+13
4E+13
3E+13
2E+13
1E+13
0
0
5E+13
1E+14
Numerosità Dillinger [1125K-1112K]
Figura3.28. Confronto tra risultati sperimentali e analitici del modello previsionale, in
termini di numerosità di precipitati al m2, per un range di temperatura di [1125K-1112K]
per i provini Dillinger.
Nelle figure 3.27 e fig.3.28 sono riportati i valori di numerosità di precipitati al
m2 rispettivamente riscontrati nei provini Voestalpine e Dillinger (nei grafici in
rosso) confrontando questi con i valori ricavati dal modello (nel grafici in blu),
che sono interpolati da una retta inclinata a 45° rispetto all’origine degli assi del
tipo y=x.
Si nota in questo modo, come ci sia l’effettiva corrispondenza tra i valori
misurati e quelli calcolati dal modello. I diversi valori di numerosità riscontrati
in uno stesso provino sono dovuti chiaramente alla variazione della velocità di
colata piuttosto che dall’utilizzo di 3 o 9 rulli (contatti), ciononostante tutti i
valori si attestano come ordine di grandezza sui medesimi ricavabili dal modello
per le temperature di interesse.
Le medesime valutazioni si possono fare osservando i grafici di fig.3.29-30-3132; che riportano nei primi due casi i valori di frazione di superficie (voestalpine
e dillinger) e negli ultimi due i valori di distanze tra precipitati (sempre per
provini voestalpine e dillinger).
128
Analisi sperimentale e confronto con il modello di simulazione
Valori calcolati
Valori sperimentali misurati
0,05
0,045
0,04
0,035
0,03
0,025
0,02
0,015
0,01
0,005
0
0
0,01
0,02
0,03
0,04
0,05
Frazione di superficie Voestalpine [1129K-1116K]
Figura3.29. Risultati sperimentali e analitici del modello previsionale, in termini di
frazione di superficie, per un range di temperatura di [1129K-1116K], provini Voestalpine.
Valori calcolati
Valori sperimentali misurati
0,09
0,08
0,07
0,06
0,05
0,04
0,03
0,02
0,01
0
0
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
Frazione di superficie Dillinger [1125K-1112K]
Figura3.30. Risultati sperimentali e analitici del modello previsionale, in termini di
frazione di superficie, per un range di temperatura di [1125K-1112K],provini Dillinger.
129
Capitolo 3
Valori calcolati
Valori sperimentali misurati
4E-07
3E-07
3E-07
2E-07
2E-07
1E-07
5E-08
0E+00
0E+00
5E-08
1E-07
2E-07
2E-07
3E-07
3E-07
4E-07
4E-07
Distanze [m] tra precipitati Voestalpine [1128K-1116K]
Figura3.31. Risultati sperimentali e analitici del modello previsionale, in termini di
distanza [m] tra precipitati, per un range di temperatura di [1128K-1116K], provini
Voestalpine.
Valori calcolati
Valori sperimentali misurati
4,5E-07
4,0E-07
3,5E-07
3,0E-07
2,5E-07
2,0E-07
1,5E-07
1,0E-07
5,0E-08
0,0E+00
0,0E+00
5,0E-08
1,0E-07
1,5E-07
2,0E-07
2,5E-07
3,0E-07
3,5E-07
Distanze [m] tra precipitati Dillinger [1125K-1112K]
Figura3.32. Risultati sperimentali e analitici del modello previsionale, in termini di
distanza [m] tra precipitati, per un range di temperatura di [1125K-1112K], provini
Dillinger.
130
CAPITOLO 4
Risultati e confronti
L'analisi dei dati contenuti nel capitolo 3 ha permesso di confrontare tra loro i
risultati sperimentali, in termini di frazione di superficie percentuale e di densità
numerica, con i valori espressi dal modello previsionale opportunamente settato
con parametri coerenti con quelli della realtà sperimentale.
Da questa analisi è emerso come il modello previsionale realizzato sia stato in
grado di elaborare dei risultati analoghi a quelli della campagna sperimentale,
superando così con successo la fase di validazione.
Alla luce di questo, nei paragrafi seguenti, sono riportati alcuni grafici elaborati
dal modello, che hanno lo scopo di dare un quadro più completo ed esauriente
delle potenzialità dello stesso, in cui, a seconda dei casi, sono stati fatti variare
dei parametri e valori rispetto ai casi presi in esame nel capitolo precedente,
mostrando così la variazione di densità numerica e/o frazione di superficie in
diverse possibili tipologie di acciai.
Capitolo 4
4.1 Variazione dell’energia di interfaccia precipitati/matrice
Una prima possibile modifica al modello originale, risulta essere quella di
variare nel modello il valore dell’energia di interfaccia tra i precipitati e la
matrice di acciaio, che fino a questo momento era stato preso come un valore
fissato pari a 0.5 J/m2 [3]. In questo caso si è voluto valutare il cambiamento
nella frazione di superficie, risultante da una variazione di tale parametro,
scegliendo tre valori in particolare, pari a 0.5, 0.45, 0.4 J/m2, come appare
evidente nella fig.4.1.
Temperatura [K]
0
200
400
600
800
1000
1200
10
Frazione superficie
1
0,1
0,01
0,001
0,0001
0,00001
j=0.5 j/m2
j=0.45 j/m2
j=0.4 j/m2
Figura 4.1. Frazione di superficie percentuale al variare dell’energia di interfaccia j, in
funzione della temperatura per un provino Dillinger.
132
Risultati e confronti
Nella fig.4.1 si mostra l’andamento della frazione di superficie, in funzione della
temperatura, al variare dell’energia di interfaccia, partendo da un medesimo
provino di tipo “Dillinger” (la cui composizione è riportata nel capitolo 3).
Studiando i grafici emerge come gli andamenti della frazione di superficie siano
analoghi nei tre diversi casi con delle particolarità: con un j pari a 0.5 J/m2, alle
alte temperature (tra i 1030K e i 1130K) si hanno valori molto bassi, inferiori
all’unità della frazione superficiale, mentre con gli altri valori di energia di
interfaccia si hanno già alle alte temperature valori che superano l’unità
percentuale. Tra i 900K circa e i 400K, che rappresenta il termine della
simulazione, viceversa i valori nei tre diversi casi sono praticamente coincidenti.
Da questo emerge come la variazione dell’energia di interfaccia incida molto di
più alle alte temperature, che non alle basse, raggiungendo valori compresi tra 1
e 2 a 400K.
4.2 Variazione percentuale del calore latente di fusione
Un altro parametro che si è andati a modificare leggermente per valutare
eventuali cambiamenti è stato il calore latente di fusione Lf del carburo di niobio
NbC. Il valore nominale, derivante da una ricerca in letteratura, risulta essere
pari a 45640,2 J/mole. Nella fattispecie questo risulta essere un valore, come
dice il termine stesso, “nominale”, soggetto quindi a piccole modifiche. Nel
programma quindi si sono realizzati i grafici della numerosità di precipitati con
tre valori di Lf pari al valore nominale, a quello maggiorato e diminuito del 10%
rispetto a tale valore.(vedi fig. 4.2).
133
Capitolo 4
Lf nominale
Lf + 10%
Lf - 10%
Numerosità [precipitati/m2]
1,2E+18
1E+18
8E+17
6E+17
4E+17
2E+17
0
0
200
400
600
800
1000
1200
Temperatura [K]
Figura 4.2. Numerosità precipitati/m2 al variare del calore latente di fusione del carburo di
niobio, in funzione della temperatura, per un provino Dillingen.
Nella fig. 4.2 sono riportati i valori della numerosità di precipitati/m2, in
funzione della temperatura, variando per l’appunto il valore del calore latente di
fusione, su una stessa tipologia di provino: dall’analisi dei grafici emerge come
all’aumentare di Lf , si abbia una maggiore precipitazione a pari temperatura,
con una “forbice” di valori che rimane sempre più o meno costante, a parte alle
alte temperature dove il parametro pare incidere in modo limitato.
4.3 Variazione della percentuale nominale di niobio
Uno degli aspetti più interessanti di cui si è indagato è stato quello di valutare
l’andamento della frazione di superficie e di numerosità di precipitati, variando
le percentuali di niobio nominali, attingendo a quelli che possono essere i
possibili valori di niobio riscontrabili nelle diverse tipologie di acciai micro
legati ad elevata resistenza. Questa analisi è stata realizzata tenendo fisso il
valore della percentuale di carbonio presente nell’acciaio, in particolare pari a
0.1% C (percentuale in peso).
134
Risultati e confronti
I diversi valori di niobio scelti sono stati i seguenti: 0.02%, 0.03%, 0.04%,
0.05%. La differenza sostanziale e fondamentale tra i differenti casi è che
variando la % di Nb, cambia la temperatura critica di precipitazione, ovvero
quella temperatura alla quale l’attività del NbC risulta pari all’unità, o, in altri
termini, quella temperatura alla quale iniziano a precipitare i carburi.
Nella tabella 4.1 vengono riportate per ogni composizione %, le diverse
temperature critiche, opportunamente valutate con il modello di temperatura.
Tabella 4.1. Temperature critiche di precipitazione del NbC, in funzione della % di niobio,
tenendo fisso il valore di carbonio (0.1%).
% niobio
0.020
0.030
0.040
0.050
Temperatura
critica [K]
1275
1317
1348
1374
Subito appare evidente come all’aumentare della % di niobio aumenti anche la
temperatura critica di precipitazione.
Nelle fig.4.3 e fig.4.4 sono riportate rispettivamente le frazione di superficie e la
numerosità di precipitati al variare della % di Nb, fissato la % di C, in funzione
della temperatura.
135
Capitolo 4
Temperatura [K]
0
200
400
600
800
1000
1200
Frazione superficie
10
1
0,1
0,01
0.020% Nb
0.030% Nb
0.040% Nb
0.050% Nb
Figura 4.3. Frazione di superficie percentuale, al variare della % di niobio, tenendo fissata
la % di C (0.1%), in funzione della temperatura.
0.02% Nb
0.03% Nb
0.04% Nb
0.05% Nb
Numerosità [precipitati/m2]
1,2E+18
1E+18
8E+17
6E+17
4E+17
2E+17
0
0
200
400
600
800
1000
1200
Temperatura [K]
Figura 4.4. Numerosità precipitati/m2 ,al variare della % di niobio, tenendo fissata la % di
C (0.1%), in funzione della temperatura.
136
Risultati e confronti
Analizzando nel dettaglio la fig.4.3 risulta evidente come ad alta temperatura (ad
esempio 1100K) la frazione di superficie per 0.04% e 0.05%, è superiore
all’unità, mentre negli altri due casi si hanno valori nettamente inferiori,
soprattutto nel caso del 0.02%. Con il diminuire della temperatura le differenze
nei differenti casi vanno sostanzialmente ad annullarsi.
4.4 Variazione della percentuale nominale di carbonio
Così come si è valutato il caso della variazione di niobio, ora si procede
valutando il cambiamento nella % di carbonio, tenendo fissa quella di niobio,
pari a 0.035%.
Nella tabella 4.2 si riportano le temperatura critiche di precipitazione per le
diverse % di carbonio scelte.
Tabella 4.2. Temperature critiche di precipitazione del NbC, in funzione della % di
carbonio, tenendo fisso il valore di niobio (0.035%).
% carbonio
0.03
0.06
0.09
0.12
0.15
Temperatura
critica [K]
1213
1280
1322
1354
1380
L’andamento delle temperature critiche rispecchia l’andamento del caso
precedente, in cui era stato fatto variare la % di niobio; nelle fig.4.5 e fig.4.6
sono riportate rispettivamente le frazione di superficie e la numerosità di
precipitati al variare della % di C, fissato la % di Nb, in funzione della
temperatura.
Il caso più particolare risulta essere quello allo 0.03% di C, in cui fino a 1000K,
la frazione di superficie è inferiore all’unità a differenza delle altre casistiche in
cui appare superiore; per il resto i valori sono molto simili tra loro sia per quanto
riguarda le frazione di superficie sia per la numerosità di precipitati.
137
Capitolo 4
Temperatura [K]
Frazione superficie
0
200
400
600
800
1000
1200
1,00E+01
1,00E+00
1,00E-01
1,00E-02
1,00E-03
1,00E-04
1,00E-05
1,00E-06
1,00E-07
1,00E-08
1,00E-09
1,00E-10
1,00E-11
0.03% C
0.06% C
0.09% C
0.12% C
0.15% C
Figura 4.5. Frazione di superficie percentuale, al variare della % di carbonio, tenendo fissa
la % di Nb (0.035%), in funzione della temperatura.
Numerosità [precipitati/m2]
1,2E+18
1E+18
8E+17
0.15% C
6E+17
0.09% C
4E+17
0.06% C
2E+17
0.03% C
0
0
200
400
600
800
1000
1200
Temperatura [K]
Figura 4.6. Numerosità precipitati/m2, al variare della % di carbonio, tenendo fissata la %
di Nb (0.035%), in funzione della temperatura.
138
Risultati e confronti
4.5 Analisi di casi particolari
Nei paragrafi precedenti, si sono trattati separatamente, i casi di variazione % di
niobio con valore fisso di carbonio e viceversa. Per avere un quadro più
completo si procede ora ad esaminare la frazione di superficie percentuale in
due casi particolari e direi “estremi”, nel senso che sono state prese in
considerazione le accoppiate %Nb-%C minime e massime possibili, rispetto ai
valori utilizzati in precedenza. L’accoppiata minima risulta essere quella allo
0.020% Nb e 0.03% C, quella massima allo 0.05% Nb e 0.17% C. Nella tabella
4.3 sono riportate per questi due casi le temperature critiche di precipitazione.
Tabella 4.3. Temperature critiche di precipitazione del NbC, in funzione della % di
carbonio e niobio.
Accoppiate Nb/C
0.02%Nb – 0.03%C
0.05%Nb – 0.17%C
Temperatura critica
[K]
1164
1439
Come appare chiaro, sono due situazione veramente estreme, che risultano avere
temperatura critiche di precipitazione veramente molto differenti, passando da
1164K per l’accoppiata minima a 1439K per quella massima. Per questo motivo
i grafici di fig. 4.7 sono molto diversi rispetto ai precedenti, nel senso che la
differenza a pari temperatura, dei valori di frazione superficiale è sensibile.
I due grafici si intersecano ad una temperatura di circa 800K, corrispondenti ad
un valore di 4.3 circa, mentre alle temperature superiori, i valori di frazione
superficiale nel caso dell’accoppiata massima sono abbondantemente superiori
all’unità. Per riscontrare in questo caso specifico valori inferiori bisognerebbe
seguire l’andamento fino a temperature vicine ai 1350-1400K, che nei grafici
non sono riportate, essendoci concentrati sull’andamento dei parametri, tra una
temperatura di 1141K e 400K. Nel caso dell’accoppiata minima partendo dalla
temperatura massima si hanno valori praticamente pari allo zero fino a 1050K.
Tra i 1050K e i 1000K si riscontrano valori compresi nell’ordine di 10-3 e 10-2
che poi crescono fino ad una temperatura di picco di poco inferiore agli 800K,
dopo la quale i valori di frazione superficiale tendono a diminuire.
139
Capitolo 4
0.020% Nb - 0.03% C
0.050% Nb - 0.17% C
6
Frazione superficie
5
4
3
2
1
0
-1
0
200
400
600
800
1000
1200
Temperatura [K]
Figura 4.7. Frazione di superficie percentuale nei casi estremi di % di C e Nb, in funzione
della temperatura.
4.6 Confronto tra diversi precipitati
Per concludere queste tipologie di analisi, dopo aver concentrato l’attenzione
fin’ora solo sul carburo di niobio NbC, risulta interessante valutare eventuali
differenze tra il tra lo stesso NbC con il nitruro di niobio (NbN) e con il nitruro
di Alluminio (AlN).
Tutti e tre questi precipitati possono essere valutati infatti adottando il modello
previsionale, stando attenti chiaramente ad utilizzare per ogni caso i corretti
valori di tutte le proprietà richieste dal modello.
Per avere un confronto tra precipitati coerente, come “base” di partenza si è
utilizzata la composizione chimica dei provini “Dillinger”, in cui si ha lo 0.17%
di carbonio, lo 0.029% di niobio, lo 0.0066% di azoto e lo 0.068% di alluminio.
140
Risultati e confronti
Nelle seguenti figure saranno valutati rispettivamente i raggi enucleati, la
frazione di superficie e la numerosità dei precipitati, in funzione della
temperatura, per i tre precipitati.
Raggi di nucleazione [m]
2,5E-09
2E-09
1,5E-09
NbC
NbN
1E-09
AlN
5E-10
0
0
200
400
600
800
1000
1200
Temperatura [K]
Figura 4.8. Raggi di nucleazione per NbC, NbN e AlN, in funzione della temperatura.
Nella fig.4.8 si mostra l’andamento dei raggi di nucleazione per i tre precipitati e
si nota come, per le temperature osservate, il nitruro di alluminio si formi in
precipitati con raggi più piccoli rispetto agli altri due, soprattutto ad alte
temperature: a 1000K il raggio corrispondente dell’AlN è 6.66*10-10m, contro
1.28*10-9m per il NbN.
141
Capitolo 4
Numerosità [precipitai/m2]
1,2E+18
1E+18
8E+17
NbC
6E+17
NbN
4E+17
AlN
2E+17
0
0
200
400
600
800
1000
1200
Temperatura [K]
Figura 4.9. Numerosità precipitati/m2, per il NbC, NbN e AlN, in funzione della
temperatura, per un provino Dillinger.
Così come appare evidente nella fig.4.8 anche nella fig.4.9 e nella fig.4.10,
risulta come il nitruro di alluminio si discosti sensibilmente dagli altri due
precipitati che grossomodo non presentano differenze così elevate tra loro.
La numerosità di precipitati per l’AlN è superiore ad ogni temperatura valutata,
rispetto agli due casi, anche se forma precipitati di dimensioni inferiori e questo
riflette l’andamento dei grafici di fig.4.10 in cui si può apprezzare come da
1050K-1000K la frazione superficiale di NbN e NbC superi quella del nitruro di
alluminio.
142
Risultati e confronti
6
Frazione superficie
5
4
NbC
3
NbN
2
AlN
1
0
0
200
400
600
800
1000
1200
Temperatura [K]
Figura 4.10. Frazione di superficie percentuale, per il NbC, NbN e AlN, in funzione della
temperatura, per un provino Dillinger.
143
Capitolo 4
144
CONCLUSIONI
Il presente lavoro di tesi è stato dedicato alla costruzione e alla validazione, di
un modello matematico dedicato alla previsione quantitativa del fenomeno di
precipitazione in acciai microlegati, durante il raffreddamento subito da tali
acciai nel processo di colata continua: considerare le variazioni cicliche del
percorso termico a cui è soggetto l’acciaio è un aspetto di fondamentale
importanza per controllare i fenomeni di formazione e sviluppo dei nano
precipitati che influenzano sia le proprietà meccaniche finali dell’acciaio, sia la
duttilità a caldo, da cui dipende l’integrità del semilavorato solidificato per
mezzo della macchina di colata continua.
La modalità di raffreddamento risulta molto particolare in quanto è
caratterizzata da una serie di raffreddamenti e riscaldamenti che promuovono
rispettivamente la nucleazione e l’ingrossamento dei nano precipitati.
Si è stabilito che un modello che tiene conto delle oscillazioni termiche, della
composizione chimica dell’acciaio, dell’estensione della superficie di bordo
grano, dell’energia di attivazione del processo di nucleazione e della diffusione
delle specie chimiche, può consentire una corretta previsione della distribuzione
dimensionale dei nano precipitati. Tramite l’utilizzo di “Scilab”, che è un
programma per il calcolo numerico finalizzato ad applicazioni scientifiche, il
modello è stato realizzato ed è stato poi validato sulla base delle caratteristiche
morfologiche e dimensionali della popolazione dei nano precipitati, individuate
attraverso esami FEG-SEM, in termini di distribuzione delle distanze tra
precipitati, di dimensione media e numerosità degli stessi precipitati.
Conclusioni
Valori calcolati
Valori sperimentali misurati
5E+13
4,5E+13
4E+13
3,5E+13
3E+13
2,5E+13
2E+13
1,5E+13
1E+13
5E+12
0
0
2E+13
4E+13
6E+13
Numerosità Voestalpine[1129K-1116K]
Figura 5.1. Confronto tra risultati sperimentali e analitici del modello previsionale, in
termini di numerosità di precipitati al m2, per un range di temperatura di [1129K-1116K]
per i provini Voestalpine.
Valori calcolati
Valori sperimentali misurati
9E+13
8E+13
7E+13
6E+13
5E+13
4E+13
3E+13
2E+13
1E+13
0
0
5E+13
1E+14
Numerosità Dillinger [1125K-1112K]
Figura 5.2. Confronto tra risultati sperimentali e analitici del modello previsionale, in
termini di numerosità di precipitati al m2, per un range di temperatura di [1125K-1112K]
per i provini Dillinger.
146
Conclusioni
I grafici precedenti illustrano l’effettiva corrispondenza tra i valori sperimentali
misurati e quelli calcolati tramite il modello, in termini di numerosità di
precipitati, per i due tipi di provini che sono stati utilizzati nella campagna
sperimentale (provini di tipo “Voestalpine” e “Dillinger” caratterizzati ognuno
da una propria composizione chimica).
Il modello realizzato può rivelarsi molto utile in ambito industriale, per i limitati
tempi computazionali oltre che per la relativa semplicità di utilizzo, che
presuppone come principali dati di input la composizione chimica dell’acciaio e
il percorso termico che esso subisce, senza dover utilizzare altre tipologie di
software più complessi e con alti tempi computazionali.
147
Conclusioni
148
APPENDICE
a) Soluzione del modello di solidificazione dell’acciaio.
Figura A.1. Simulazione del dominio della matrice.
La figura mostra la simulazione del dominio nell’acciaio in solidificazione, che
è parte liquido e parte solido e si muove ad una velocità di colata Vc. Applicando
le condizioni al contorno:
(A.1)
(A.2)
L’eq.(1.1) è risolta per ogni istante temporale usando la seguente
discretizzazione.
Appendice
(1) nodo liquido al centro linea
(A.3)
(2) nodi interni
(A.4)
(3) nodo in superficie della matrice
(A.5)
L’effetto del surriscaldamento è incluso nell’equazione (A.4) per il primo nodo
interno con una temperatura al di sotto di quella del liquidus:
(A.6)
Dove dx = x per nodi interni e dx =x/2 per nodi al contorno.
Le eq. precedenti sono risolte a ogni passo temporale (Tinew) basandosi
sulle proprietà valutate al passo precedente (Ti).
Questo semplice schema esplicito di solito è accettabile perché le modifiche
delle proprietà sono generalmente graduali con la temperatura.
150
Appendice
Tuttavia, il calore specifico efficace ha un salto improvviso quando la
temperatura scende sotto la temperatura di liquidus.
Per migliorare la precisione e permettere un passo temporale più grande , una
correzione post-iterazione è applicata a ciascun nodo dopo il passo temporale,
quando il primo scende sotto la temperatura di liquidus.
(A.7)
b) Spessore lingottiera
Per una lingottiera curva, lo spessore dmold, varia con la distanza ed è calcolato
per il raggio esterno ed interno delle facce della lingottiera separatamente:
(B.1)
(B.2)
Dove dmold è lo spessore all’inizio della lingottiera, Zmold-total è la lunghezza totale
della lingottiera, e RO E RI sono i raggi esterni ed interni della lingottiera.
151
Appendice
c) Temperature
Temperatura del liquidus, solidus e peritettica dipende dalla composizione
dell’acciaio come segue:
(C.1)
(C.2)
(C.3)
Cr è il tasso di raffreddamento, C0 è la composizione dell’acciaio.
Tabella C.1. Dati per il modello.
152
Appendice
d) funzioni
Funzioni delle proprietà termiche dell’acciaio al carbonio:
(1) conduttività termica
Figura D.1. Coefficienti conduttività termica.
(2) calore specifico
Figura D.2. Calore specifico.
153
Appendice
(3) densità utilizzata per l’espansione lineare termica
Figura D.3. Coefficienti di densità.
e) Modello nucleazione ed accrescimento NbC
clear all
clc
//modello nucleazione ed accrescimento
//composto di interesse NbC, dove nel listato M è il niobio, X è il carbonio
X0=0.17;
//vedi sopra (quelli riportati sono numeri di esempio)
x=1;
//coeff.stechiometrici del composto MxXy (quelli riportati sono numeri di
esempio nel caso NbC)
y=1;
AM=92.91;
//masse atomiche degli elementi M e X (g/mol) del niobio è 92.91(g/mol)
mentre del carbonio è 12.01 (g/mol)
AX=12.01;
Vp=13.39*10^(-6);
//volume molare struttura cristallina precipitata(NbC)(m3/mol)
sigma=0.5;
//0.5 o 0.3 negli esempi//energia di interfaccia tra le particelle precipitate e
la fase della matrice metallica(J/m2)
MM=AM+AX;
//massa molecolare del composto
Lf=((435000*MM)/1000); //calore latente NbC(j/mole)
kb=1.3806*10^(-23);
//costante di Boltzmann (J/K)
Rg=8.314;
//costante dei gas (J*K-1*mol-1)
//Individuata la Tcritica e il tg corrispondente nel programma "modellotemperatura", si procede
con la determinazione dell'andamento delle concentrazioni dei due elementi all'equilibrio
dt=1;
//passo di tempo
tempofinale=80;
//istante finale di tempo
tg=tempofinale;
154
Appendice
M0(tg)=zeros(tempofinale);
M0(:)=0.029;
for tg=1:dt:tempofinale
Tcritica=1242;
//ovvero quella di inizio ciclo
T(tg)=-0.0006*tg^3+0.0635*tg^2-3.249*tg+1195.5;
//temperatura in Kelvin[1126-tg]
//il prodotto di solubilità K varia in base alla fase in cui ci si trova ed i valori riportati fanno
riferimento al NbC.
K(tg)=10^((-7020/T(tg))+2.81); //vedere se tenere un solo "valore" o variare lineramente con
il valore in alfa
Mequilibrio(tg)=(1*K(tg))/X0;
//concentrazione all'equilibrio dell'elemento M
if T(tg)>1185 then
D(tg)=0.83*10^(-4)*(%e^(-266500/(Rg*T(tg))));
else
D(tg)=50.2*10^(-4)*(%e^(-252000/(Rg*T(tg))));
matrice(m2/s), valori riferiti al niobio
end
deltaTn(tg)=T(tg)-Tcritica;
quella critica
deltaC(tg)=M0(tg)-Mequilibrio(tg);
lega e quella all'equilibrio per ogni T
//coeff.di diffusione nella fase della
//differenza tra temperature di esercizio e
//differenza tra concentrazione iniziale in
//////////////////////divido i ciclo for tg solo per ordine e maggior chiarezza
num=tg;
r(tg,num)=(-2*sigma*Tcritica*Vp)/(deltaTn(tg)*Lf);
istante (m)
V(tg,num)=(4/3)*%pi*(r(tg,num))^3;
A(tg,num)=4*%pi*(r(tg,num))^2;
//raggi di nucleazione istante per
if num<tempofinale then
incrementovolume(tg,num)=A(tg,num)*D(tg)*(deltaC(tg)/(10^(-10)))*dt;
incremento volumetrico che sarà poi diverso negli altri istanti di tempo
V(tg+1,num)=V(tg,num)+incrementovolume(tg,num);
r(tg+1,num)=((V(tg+1,num)*3)/(4*%pi))^(1/3);
A(tg+1,num)=4*%pi*(r(tg+1,num))^2;
velo(tg,num)=(r(tg+1,num)-r(tg,num))/dt;
incrementovolume(tg+1,num)=A(tg+1,num)*velo(tg,num)*deltaC(tg)*dt;
//primo
deltaGN(tg,num)=(4*%pi*(r(tg,num)^2)*sigma+(((4/3)*%pi*(r(tg,num)^3)*Lf*deltaTn(tg))/(T
critica*Vp)))*0.01; //varia. dell'en. libera del sistema dopo la formazione dei nuclei stabili
N0=1.236*10^18;
Nn(tg,num)=N0*exp(-deltaGN(tg,num)/(kb*Tcritica));
end
155
Appendice
deltaGN(tg,num)=(4*%pi*(r(tg,num)^2)*sigma+(((4/3)*%pi*(r(tg,num)^3)*Lf*deltaTn(tg))/(T
critica*Vp)))*0.01; //varia. dell'en. libera del sistema dopo la formazione dei nuclei stabili
N0=1.236*10^18;
Nn(tg,num)=N0*exp(-deltaGN(tg,num)/(kb*Tcritica));
//Nn(tg+1,num)=Nn(tg,num);
sommaNn(tg)=trace(Nn);
if tg==num & tg<tempofinale then
sommavelo(tg)=velo(tg,num);
end
if tg==num &tg<tempofinale then
sommaA(tg)=sum(A(tg,num));
end
if tg<tempofinale & sommaNn>0 then
Temperatura(tg)=T(tg);
lcritica(tg)=(M0(tg)*D(tg))/(deltaC(tg)*sommavelo(1));
l(tg)=((1/sommaNn(tg))^(1/2));
if l<lcritica then
M0(tg)=(l(tg)*sommavelo(tg)*deltaC(tg))/(D(tg));
else
M0(tg)=M0(tg);
end
deltaC(tg)=M0(tg)-Mequilibrio(tg);
end
RR=diag(r);
NN=diag(Nn);
a=length(RR);
b=length(NN);
end
//gli altri istanti di tempo seguono questi cicli
for num=1:tempofinale-2
for tg=num+2:tempofinale
V(tg,num)=V(tg-1,num)+incrementovolume(tg-1,num);
r(tg,num)=((V(tg,num)*3)/(4*%pi))^(1/3);
A(tg,num)=4*%pi*(r(tg,num))^2;
velo(tg,num)=(r(tg,num)-r(tg-1,num))/dt;
incrementovolume(tg,num)=A(tg,num)*velo(tg,num)*deltaC(tg)*dt;
Nn(tg,num)=Nn(tg-1,num);
end
end
156
Appendice
for i=1:a
for j=1:b
if i==j then
Ntotali(i)=NN(j)*(4)*%pi*((RR(i))^2)*10;
end
end
end
f) Modello nucleazione ed accrescimento NbN
clear all
clc
//modello nucleazione ed accrescimento
//composto di interesse NbN, dove nel listato M è il niobio, X è l'azoto
X0=0.0066;
//vedi sopra (quelli riportati sono numeri di esempio)
x=1;
//coeff.stechiometrici del composto MxXy (quelli riportati sono numeri di
esempio nel caso NbN)
y=1;
AM=92.91;
//masse atomiche degli elementi M e X (g/mol) del niobio è 92.91(g/mol)
mentre dell'azoto è 14(g/mol)
AX=14;
Vp=9.7*10^(-6);
//volume molare struttura cristallina precipitata(NbN)(m3/mol)
sigma=0.5;
//0.5 o 0.3 negli esempi//energia di interfaccia tra le particelle precipitate e
la fase della matrice metallica(J/m2)
MM=AM+AX;
//massa molecolare del composto
Lf=(272000*MM)/1000; //calore latente NbN(j/mole)
kb=1.3806*10^(-23);
//costante di Boltzmann (J/K)
Rg=8.314;
//costante dei gas (J*K-1*mol-1)
//Individuata la Tcritica e il tg corrispondente nel programma "modellotemperatura", si procede
con la determinazione dell'andamento delle concentrazioni dei due elementi all'equilibrio
dt=1;
//passo di tempo
tempofinale=742;
//istante finale di tempo
tg=tempofinale;
M0(tg)=zeros(tempofinale);
M0(:)=0.029;
for tg=1:dt:tempofinale
Tcritica=1352;
T(tg)=[1142-tg];
//ovvero quella di inizio ciclo
//temperatura in Kelvin
//il prodotto di solubilità K varia in base alla fase in cui ci si trova ed i valori riportati fanno
riferimento al NbN.
K(tg)=10^((-10150/T(tg))+3.79); //vedere se tenere un solo "valore" o variare lineramente con
il valore in alfa
157
Appendice
Mequilibrio(tg)=(1*K(tg))/X0;
//concentrazione all'equilibrio dell'elemento M
if T(tg)>1185 then
D(tg)=0.83*10^(-4)*(%e^(-266500/(Rg*T(tg))));
else
D(tg)=50.2*10^(-4)*(%e^(-252000/(Rg*T(tg))));
matrice(m2/s), valori riferiti al niobio
end
deltaTn(tg)=T(tg)-Tcritica;
quella critica
deltaC(tg)=M0(tg)-Mequilibrio(tg);
lega e quella all'equilibrio per ogni T
//coeff.di diffusione nella fase della
//differenza tra temperature di esercizio e
//differenza tra concentrazione iniziale in
//////////////////////divido i ciclo for tg solo per ordine e maggior chiarezza
num=tg;
r(tg,num)=(-2*sigma*Tcritica*Vp)/(deltaTn(tg)*Lf);
istante (m)
V(tg,num)=(4/3)*%pi*(r(tg,num))^3;
A(tg,num)=4*%pi*(r(tg,num))^2;
//raggi di nucleazione istante per
if num<tempofinale then
incrementovolume(tg,num)=A(tg,num)*D(tg)*(deltaC(tg)/(10^(-10)))*dt;
incremento volumetrico che sarà poi diverso negli altri istanti di tempo
V(tg+1,num)=V(tg,num)+incrementovolume(tg,num);
r(tg+1,num)=((V(tg+1,num)*3)/(4*%pi))^(1/3);
A(tg+1,num)=4*%pi*(r(tg+1,num))^2;
velo(tg,num)=(r(tg+1,num)-r(tg,num))/dt;
incrementovolume(tg+1,num)=A(tg+1,num)*velo(tg,num)*deltaC(tg)*dt;
//primo
deltaGN(tg,num)=(4*%pi*(r(tg,num)^2)*sigma+(((4/3)*%pi*(r(tg,num)^3)*Lf*deltaTn(tg))/(T
critica*Vp)))*0.01; //varia. dell'en. libera del sistema dopo la formazione dei nuclei stabili
N0=1.236*10^18;
Nn(tg,num)=N0*exp(-deltaGN(tg,num)/(kb*Tcritica));
end
deltaGN(tg,num)=(4*%pi*(r(tg,num)^2)*sigma+(((4/3)*%pi*(r(tg,num)^3)*Lf*deltaTn(tg))/(T
critica*Vp)))*0.01; //varia. dell'en. libera del sistema dopo la formazione dei nuclei stabili
N0=1.236*10^18;
Nn(tg,num)=N0*exp(-deltaGN(tg,num)/(kb*Tcritica));
//Nn(tg+1,num)=Nn(tg,num);
sommaNn(tg)=trace(Nn);
if tg==num & tg<tempofinale then
sommavelo(tg)=velo(tg,num);
end
if tg==num &tg<tempofinale then
158
Appendice
sommaA(tg)=sum(A(tg,num));
end
if tg<tempofinale & sommaNn>0 then
Temperatura(tg)=T(tg);
l(tg)=(1/sommaNn(tg))^(1/2);
lcritica(tg)=(M0(tg)*D(tg))/(deltaC(tg)*sommavelo(tg));
if l<lcritica then
M0(tg)=(l(tg)*sommavelo(tg)*deltaC(tg))/(D(tg));
else
M0(tg)=M0(tg);
end
deltaC(tg)=M0(tg)-Mequilibrio(tg);
end
RR=diag(r);
NN=diag(Nn);
a=length(RR);
b=length(NN);
end
//gli altri istanti di tempo seguono questi cicli
for num=1:tempofinale-2
for tg=num+2:tempofinale
V(tg,num)=V(tg-1,num)+incrementovolume(tg-1,num);
r(tg,num)=((V(tg,num)*3)/(4*%pi))^(1/3);
A(tg,num)=4*%pi*(r(tg,num))^2;
velo(tg,num)=(r(tg,num)-r(tg-1,num))/dt;
incrementovolume(tg,num)=A(tg,num)*velo(tg,num)*deltaC(tg)*dt;
Nn(tg,num)=Nn(tg-1,num);
end
end
for i=1:a
for j=1:b
if i==j then
Ntotali(i)=NN(j)*(4)*%pi*(RR(i))^2;
end
end
end
159
Appendice
g) Modello nucleazione ed accrescimento AlN
clear all
clc
//modello nucleazione ed accrescimento
//composto di interesse AlN, dove nel listato M è l'alluminio, X è l'azoto
X0=0.0066;
//vedi sopra (quelli riportati sono numeri di esempio)
x=1;
//coeff.stechiometrici del composto MxXy (quelli riportati sono numeri di
esempio nel caso AlN)
y=1;
AM=26.98;
//masse atomiche degli elementi M e X (g/mol) dell'alluminio è
26.98(g/mol) mentre dell'azoto è 14(g/mol)
AX=14;
Vp=12.54*10^(-6);
//volume molare struttura cristallina precipitata(AlN)(m3/mol)
sigma=0.5;
//0.5 o 0.3 negli esempi//energia di interfaccia tra le particelle precipitate e
la fase della matrice metallica(J/m2)
MM=AM+AX;
//massa molecolare del composto
Lf=(1300000*MM)/1000; //calore latente AlN(j/mole)
kb=1.3806*10^(-23);
//costante di Boltzmann (J/K)
Rg=8.314;
//costante dei gas (J*K-1*mol-1)
//Individuata la Tcritica e il tg corrispondente nel programma "modellotemperatura", si procede
con la determinazione dell'andamento delle concentrazioni dei due elementi all'equilibrio
dt=1;
//passo di tempo
tempofinale=642;
//istante finale di tempo
tg=tempofinale;
M0(tg)=zeros(tempofinale);
M0(:)=0.068;
for tg=1:dt:tempofinale
Tcritica=1547;
T(tg)=[1442-tg];
//ovvero quella di inizio ciclo
//temperatura in Kelvin
//il prodotto di solubilità K varia in base alla fase in cui ci si trova ed i valori riportati fanno
riferimento al AlN, questo K si riferisce alla fase austenitica
K(tg)=10^((-6770/T(tg))+1.03); //vedere se tenere un solo "valore" o variare lineramente con
il valore in alfa
Mequilibrio(tg)=(1*K(tg))/X0;
//concentrazione all'equilibrio dell'elemento M
if T(tg)>1185 then
D(tg)=2.51*10^(-4)*(%e^(-253400/(Rg*T(tg))));
else
D(tg)=0.3*10^(-2)*(%e^(-234500/(Rg*T(tg))));
matrice(m2/s), valori riferiti all'alluminio
end
160
//coeff.di diffusione nella fase della
Appendice
deltaTn(tg)=T(tg)-Tcritica;
quella critica
deltaC(tg)=M0(tg)-Mequilibrio(tg);
lega e quella all'equilibrio per ogni T
//differenza tra temperature di esercizio e
//differenza tra concentrazione iniziale in
//////////////////////divido i ciclo for tg solo per ordine e maggior chiarezza
num=tg;
r(tg,num)=(-2*sigma*Tcritica*Vp)/(deltaTn(tg)*Lf);
istante (m)
V(tg,num)=(4/3)*%pi*(r(tg,num))^3;
A(tg,num)=4*%pi*(r(tg,num))^2;
//raggi di nucleazione istante per
if num<tempofinale then
incrementovolume(tg,num)=A(tg,num)*D(tg)*(deltaC(tg)/(10^(-10)))*dt;
incremento volumetrico che sarà poi diverso negli altri istanti di tempo
V(tg+1,num)=V(tg,num)+incrementovolume(tg,num);
r(tg+1,num)=((V(tg+1,num)*3)/(4*%pi))^(1/3);
A(tg+1,num)=4*%pi*(r(tg+1,num))^2;
velo(tg,num)=(r(tg+1,num)-r(tg,num))/dt;
incrementovolume(tg+1,num)=A(tg+1,num)*velo(tg,num)*deltaC(tg)*dt;
//primo
deltaGN(tg,num)=(4*%pi*(r(tg,num)^2)*sigma+(((4/3)*%pi*(r(tg,num)^3)*Lf*deltaTn(tg))/(T
critica*Vp)))*0.01; //varia. dell'en. libera del sistema dopo la formazione dei nuclei stabili
N0=1.236*10^18;
Nn(tg,num)=N0*exp(-deltaGN(tg,num)/(kb*Tcritica));
end
deltaGN(tg,num)=(4*%pi*(r(tg,num)^2)*sigma+(((4/3)*%pi*(r(tg,num)^3)*Lf*deltaTn(tg))/(T
critica*Vp)))*0.01; //varia. dell'en. libera del sistema dopo la formazione dei nuclei stabili
N0=1.236*10^18;
Nn(tg,num)=N0*exp(-deltaGN(tg,num)/(kb*Tcritica));
//Nn(tg+1,num)=Nn(tg,num);
sommaNn(tg)=trace(Nn);
if tg==num & tg<tempofinale then
sommavelo(tg)=velo(tg,num);
end
if tg==num &tg<tempofinale then
sommaA(tg)=sum(A(tg,num));
end
if tg<tempofinale & sommaNn>0 then
Temperatura(tg)=T(tg);
l(tg)=(1/sommaNn(tg))^(1/2);
lcritica(tg)=(M0(tg)*D(tg))/(deltaC(tg)*sommavelo(tg));
if l<lcritica then
M0(tg)=(l(tg)*sommavelo(tg)*deltaC(tg))/(D(tg));
else
161
Appendice
M0(tg)=M0(tg);
end
deltaC(tg)=M0(tg)-Mequilibrio(tg);
end
RR=diag(r);
NN=diag(Nn);
a=length(RR);
b=length(NN);
end
//gli altri istanti di tempo seguono questi cicli
for num=1:tempofinale-2
for tg=num+2:tempofinale
V(tg,num)=V(tg-1,num)+incrementovolume(tg-1,num);
r(tg,num)=((V(tg,num)*3)/(4*%pi))^(1/3);
A(tg,num)=4*%pi*(r(tg,num))^2;
velo(tg,num)=(r(tg,num)-r(tg-1,num))/dt;
incrementovolume(tg,num)=A(tg,num)*velo(tg,num)*deltaC(tg)*dt;
Nn(tg,num)=Nn(tg-1,num);
end
end
for i=1:a
for j=1:b
if i==j then
Ntotali(i)=NN(j)*(4)*%pi*(RR(i))^2;
end
end
end
h) Modello temperatura NbC
clear all
clc
//modello temperatura critica NbC
//composto di interesse NbC, dove nel listato M è il niobio, X è il carbonio
M0=0.029;
//concentrazione dell'elemento M nella composizione dell'acciao (wt pct)
X0=0.17;
//vedi sopra (quelli riportati sono numeri di esempio)
x=1;
//coeff.stechiometrici del composto MxXy (quelli riportati sono numeri di
esempio nel caso NbC)
y=1;
AM=92.91;
//masse atomiche degli elementi M e X (g/mol) del niobio è 92.91(g/mol)
mentre del carbonio è 12.01 (g/mol)
AX=12.01;
162
Appendice
Vp=13.39*10^(-6);
//volume molare struttura cristallina precipitata(NbC) (m3/mol)
sigma=0.5;
//0.5 o 0.3 negli esempi//energia di interfaccia tra le particelle precipitate e
la fase della matrice metallica(J/m2)
MM=AM+AX;
//massa molecolare del composto
Lf=(435000*MM)/1000; //calore latente NbC(j/mole)
kb=1.3806*10^(-23);
//costante di Boltzmann(J/K)
Rg=8.314;
//costante dei gas (J*K-1*mol-1)
///////////////////////////////////////////////////////////////////////////////
//PROCEDURA PER DETERMINARE LA TEMPERATURA CRITICA DI SOLIDIFICAZIONE
///////////////////////////////////////////////////////////////////////////////
dt=1;
//passo di tempo
for tg=1:dt:1300
T(tg)=[1600-tg];
//temperatura in Kelvin
coeffM=1;
//coeff.attività degli elementi M e X, approssimati in questo caso a 1, così
da far coincidere attività e concentrazione effettiva
coeffX=1;
aM=coeffM*M0;
//attività di M e X
aX=coeffX*X0;
//il prodotto di solubilità K varia in base alla fase in cui ci si trova ed i valori riportati fanno
riferimento al NbC, il seguente K si riferisce alla fase austenitica.
K(tg)=10^((-7020/T(tg))+2.81);
activity(tg)=(M0*X0)/K(tg);
//attività del composto di interesse che varia nel tempo e
interessa sapere a quale T e di conseguenza a quale tg diventa pari all'unità
if activity(tg)<1
a=T(tg);
b=tg;
end
end
i)Modello temperatura NbN
clear all
clc
//modello temperatura critica NbN
//composto di interesse NbN, dove nel listato M è il niobio, X è l'azoto
M0=0.029;
//concentrazione dell'elemento M nella composizione dell'acciao (wt pct)
X0=0.0066;
//vedi sopra (quelli riportati sono numeri di esempio)
x=1;
//coeff.stechiometrici del composto MxXy (quelli riportati sono numeri di
esempio nel caso NbN)
y=1;
AM=92.91;
//masse atomiche degli elementi M e X (g/mol) del niobio è 92.91(g/mol)
mentre dell'azoto è 14 (g/mol)
AX=14;
Vp=9.7*10^(-6);
//volume molare struttura cristallina precipitata(NbN) (m3/mol)
sigma=0.5;
//0.5 o 0.3 negli esempi//energia di interfaccia tra le particelle precipitate e
la fase della matrice metallica(J/m2)
MM=AM+AX;
//massa molecolare del composto
Lf=(272000*MM)/1000; //calore latente NbN(j/mole)
163
Appendice
kb=1.3806*10^(-23);
//costante di Boltzmann(J/K)
Rg=8.314;
//costante dei gas (J*K-1*mol-1)
///////////////////////////////////////////////////////////////////////////////
//PROCEDURA PER DETERMINARE LA TEMPERATURA CRITICA DI SOLIDIFICAZIONE
///////////////////////////////////////////////////////////////////////////////
dt=1;
//passo di tempo
for tg=1:dt:1300
T(tg)=[1600-tg];
//temperatura in Kelvin
coeffM=1;
//coeff.attività degli elementi M e X, approssimati in questo caso a 1, così
da far coincidere attività e concentrazione effettiva
coeffX=1;
aM=coeffM*M0;
//attività di M e X
aX=coeffX*X0;
//il prodotto di solubilità K varia in base alla fase in cui ci si trova ed i valori riportati fanno
riferimento al NbN.
K(tg)=10^((-10150/T(tg))+3.79);
activity(tg)=(M0*X0)/K(tg);
//attività del composto di interesse che varia nel tempo e
interessa sapere a quale T e di conseguenza a quale tg diventa pari all'unità
if activity(tg)<1
a=T(tg);
b=tg;
end
end
l) Modello temperatura AlN
clear all
clc
//modello temperatura critica AlN
//composto di interesse AlN, dove nel listato M è l'alluminio, X è l'azoto
M0=0.068;
//concentrazione dell'elemento M nella composizione dell'acciao (wt pct)
X0=0.0066;
//vedi sopra (quelli riportati sono numeri di esempio)
x=1;
//coeff.stechiometrici del composto MxXy (quelli riportati sono numeri di
esempio nel caso AlN)
y=1;
AM=26.98;
//masse atomiche degli elementi M e X (g/mol) dell'allumnio è
26.98(g/mol) mentre dell'azoto è 14 (g/mol)
AX=14;
Vp=12.54*10^(-6);
//volume molare struttura cristallina precipitata(AlN) (m3/mol)
sigma=0.5;
//0.5 o 0.3 negli esempi//energia di interfaccia tra le particelle precipitate e
la fase della matrice metallica(J/m2)
MM=AM+AX;
//massa molecolare del composto
164
Appendice
Lf=(1300000*MM)/1000; //calore latente AlN(j/mole)
kb=1.3806*10^(-23);
//costante di Boltzmann(J/K)
Rg=8.314;
//costante dei gas (J*K-1*mol-1)
///////////////////////////////////////////////////////////////////////////////
//PROCEDURA PER DETERMINARE LA TEMPERATURA CRITICA DI SOLIDIFICAZIONE
///////////////////////////////////////////////////////////////////////////////
dt=1;
//passo di tempo
for tg=1:dt:1300
T(tg)=[1600-tg];
//temperatura in Kelvin
coeffM=1;
//coeff.attività degli elementi M e X, approssimati in questo caso a 1, così
da far coincidere attività e concentrazione effettiva
coeffX=1;
aM=coeffM*M0;
//attività di M e X
aX=coeffX*X0;
//il prodotto di solubilità K varia in base alla fase in cui ci si trova ed i valori riportati fanno
riferimento al AlN.
K(tg)=10^((-6770/T(tg))+1.03);
activity(tg)=(M0*X0)/K(tg);
//attività del composto di interesse che varia nel tempo e
interessa sapere a quale T e di conseguenza a quale tg diventa pari all'unità
if activity(tg)<1
a=T(tg);
b=tg;
end
end
m) Modello siti di nucleazione
clear all
clc
facce=12
r=0.6*10^(-6)
a=(r*2)/(2^(1/2))
A=(6+12*(3^(1/3)))*a^2
V=((5/3)*(2^(1/2)))*a^3
//numero facce ottaedro troncato
//raggio del grano
//spigolo dell'ottaedro troncato
//superficie
//volume
nottaedri=1/V
//numero ottaedri
Superficietot=(nottaedri*A)/facce
//superficie totale di nucleazione
//ora valuto quanti sono i siti di nucleazione
distanza=0.5*10^(-6)
supgradiente=(distanza^2)*%pi
numerositi=Superficietot/supgradiente
165
Appendice
166
Bibliografia
[1] DONNAY, B. and GROBER, H., 2001. Niobium in high strength weldable
beams and other structurals, Proceedings of theInternational Symposium
“Niobium 2001”, Orlando FL USA 2001.
[2] JANSTO, S., 2007. Niobium in structural steel and long product
applications. 2007 International Conference on Microalloyed Steels:
Processing, Microstructure, Properties and Performance Proceedings, , pp. 4355.
[3] Kun Xu, Brian G.Thomas, Myra S.Dyer, John G.Speer and David
K.Matlock; “Model of Microalloy Precipitation During Continuous Casting and
Reheating”, this paper was presented at AISTech 2011 – The Iron & Steel
Technology Conference and Exposition.
[4] Ya Meng, Brian G.Thomas; “Heat-Transfer and Solidification Model of
Continuous Slab Casting: CON1D”
[5] Kun Xu, Brian G.Thomas e Ron O’Malley; “Equilibrium Model of
Precipitation in Microalloyed Steels”. DOI: 10.1007/s11661-010-0428-7. “The
Minerals, Metals & Materials Society and ASM International 2010.
[6] Kun Xu, Brian G.Thomas; “Particle-Size-Grouping Model of Precipitation
Kinetics in Microalloyed Steels” DOI: 10.1007/s11661-011-0938-y “The
Minerals, Metals & Materials Society and ASM International 2011.
[7] Walter Nicodemi, Carlo Mapelli; “Siderurgia” AIM 2011 ISBN 8885298818,
9788885298811
[8] http://it.wikipedia.org/wiki/William_Thomson
[9] http://it.wikipedia.org/wiki/Ottaedro_troncato,
http://www.gobnf.com/formule/default.aspx?code=0010118LKBP1
168
Ringraziamenti
Desidero ringraziare il professore Carlo Mapelli per la professionalità ed enorme
disponibilità che mi ha dimostrato nel periodo di preparazione della tesi.
Ringrazio inoltre Andrea Gruttadauria, Davide Mombelli e Silvia Barella per
l’aiuto ed i preziosi consigli profusi nei miei confronti.
Al termine di questa esperienza al Politecnico, mi sento inoltre di dedicare un
ringraziamento particolare a quelle persone che più di altre mi sono state vicine:
Alla mia famiglia, che mi ha sempre sostenuto e che mi ha permesso di
raggiungere questo importante obiettivo che mi ero prefissato.
Ai miei amici di sempre, quelli di Tortona, a cui non potrei mai rinunciare.
Al ‘socio’, che mi ha supportato, spronato nei momenti più duri ed incoraggiato
sempre, aiutandomi ad affrontare serenamente le difficoltà che ho incontrato
(non solo al Poli) e a superarle.
Ai miei amici/colleghi “ing.”, con cui ho condiviso prima i tre anni di studi a
Pavia e poi questi ultimi a Milano… condiviso le difficoltà di ambientamento, le
gioie, le tensioni e senza i quali sarebbe stato impossibile tagliare questo
traguardo.
170