CONTROLLI AUTOMATICI (01AKSHK)
IV esercitazione presso il LAIB
Simulazione di un motore elettrico controllato in velocità mediante controllo P e PD
Si consideri un motore elettrico comandato in armatura, descritto dalle equazioni:
dia (t)
= −Ra ia (t) − Km ω(t) + va (t)
dt
dω(t)
= Km ia (t) − βω(t) − Td (t)
J
dt
La tensione di armatura va (t) è fornita da un attuatore avente ingresso u(t) e descritto dalle
equazioni:
KP W M
dva (t)
= [vi (t) − Rs ia (t)]
dt
τa
dvi (t)
= u(t)
dt
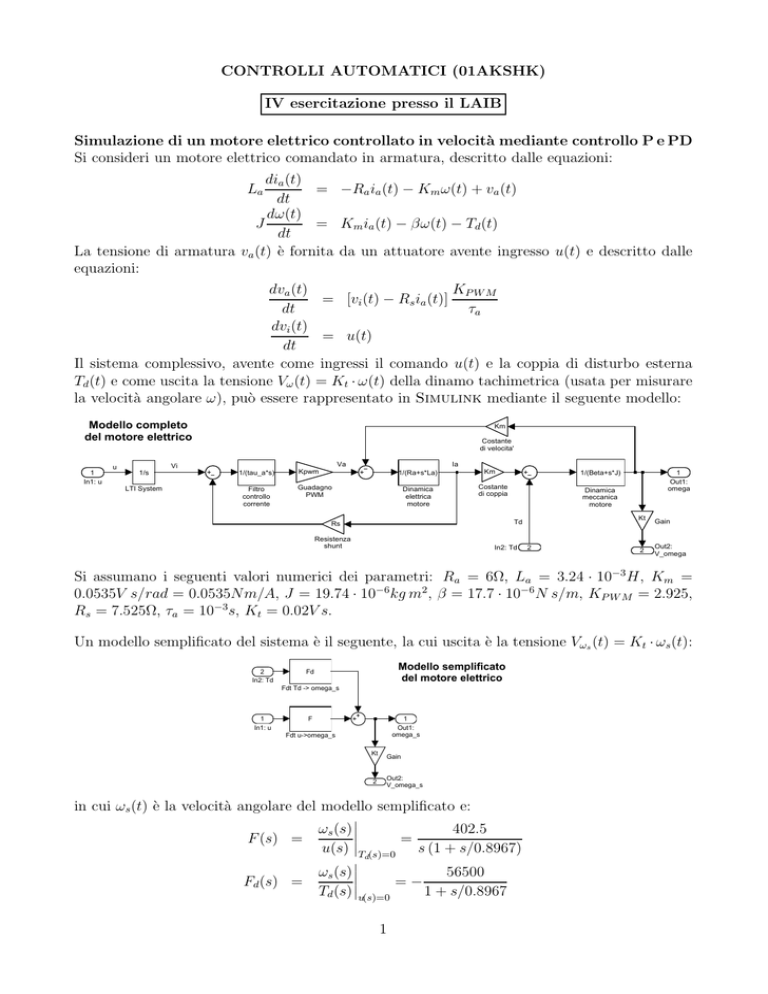
Il sistema complessivo, avente come ingressi il comando u(t) e la coppia di disturbo esterna
Td (t) e come uscita la tensione Vω (t) = Kt · ω(t) della dinamo tachimetrica (usata per misurare
la velocità angolare ω), può essere rappresentato in Simulink mediante il seguente modello:
La
Modello completo
del motore elettrico
1
In1: u
u
Km
Costante
di velocita'
Va
Vi
1/s
LTI System
1/(tau_a*s)
Filtro
controllo
corrente
Ia
Kpwm
1/(Ra+s*La)
Guadagno
PWM
Dinamica
elettrica
motore
Km
1/(Beta+s*J)
Costante
di coppia
Dinamica
meccanica
motore
Td
Rs
Resistenza
shunt
1
Out1:
omega
In2: Td
2
Kt
Gain
2
Out2:
V_omega
Si assumano i seguenti valori numerici dei parametri: Ra = 6Ω, La = 3.24 · 10−3 H, Km =
0.0535V s/rad = 0.0535Nm/A, J = 19.74 · 10−6 kg m2 , β = 17.7 · 10−6 N s/m, KP W M = 2.925,
Rs = 7.525Ω, τa = 10−3s, Kt = 0.02V s.
Un modello semplificato del sistema è il seguente, la cui uscita è la tensione Vωs (t) = Kt · ωs (t):
2
In2: Td
Modello semplificato
del motore elettrico
Fd
Fdt Td -> omega_s
1
In1: u
F
1
Out1:
omega_s
Fdt u->omega_s
Kt
2
Gain
Out2:
V_omega_s
in cui ωs (t) è la velocità angolare del modello semplificato e:
F (s) =
402.5
ωs (s) =
u(s) Td(s)=0 s (1 + s/0.8967)
Fd (s) =
ωs (s) 56500
=−
Td (s) u(s)=0
1 + s/0.8967
1
1. Simulazione del sistema in catena chiusa con controllo proporzionale assegnato
Al fine di controllare la velocità angolare del motore, si consideri il sistema di controllo in catena
chiusa costituito da un controllore P (proporzionale) Kp = 0.02 e da una retroazione unitaria
negativa, ottenendo cosı̀ un sistema controllato avente come ingressi il segnale di riferimento
Vωrif (t), proporzionale alla velocità angolare di riferimento ωrif (t), e la coppia di disturbo
esterna Td (t).
Mediante Simulink, confrontare il comportamento del sistema rappresentato dai due modelli,
confrontando fra loro gli andamenti delle uscite Vω (t) e Vωs (t) con il riferimento Vωrif (t):
1. Vωrif (t) = ε(t), Td (t) = 0;
2. Vωrif (t) = ε(t), Td (t) = 10−4 Nm.
Nella figura sottostante è riportato un possibile modello di simulazione di Simulink:
V_omega_rif
Kp
Step
In1: u
Out1: omega
Gain1
In2: Td
Td
Constant
Out2: V_omega
velocità
angolari
SubSystem1:
Modello completo
del motore elettrico
Kp
In1: u
Out1: omega_s
Gain2
In2: Td
Out2: V_omega_s
SubSystem2:
Modello semplificato
del motore elettrico
Tensioni
Suggerimento: si consiglia di usare due distinti blocchi Subsystem (in Simulink/Ports &
Subsystems) al cui interno vanno racchiusi i due modelli precedentemente descritti. All’interno
di ogni blocco Subsystem, occorre utilizzare i blocchi In1 ed Out1 (in Simulink/Ports &
Subsystems) per definire rispettivamente le porte di ingresso e di uscita del sottosistema.
2. Simulazione del sistema in catena chiusa al variare del controllo proporzionale
Considerando il solo modello semplificato, si analizzino le proprietà del sistema di controllo in
catena chiusa costituito da un controllore P (proporzionale) C(s) = Kp e da una retroazione
unitaria negativa. Per Kp = 10, 1, 0.1 e 0.02, determinare con Matlab i seguenti parametri:
1. margine di fase mϕ , margine di guadagno MG , pulsazione di taglio ωc (suggerimento:
utilizzare la funzione margin applicata alla funzione di trasferimento d’anello Ga (s));
2. banda passante B3 ed eventuale picco di risonanza Mr della funzione di trasferimento ad
anello chiuso W (s) (suggerimento: utilizzare la funzione bode);
3. tempo di salita ts ed eventuale sovraelongazione ŝ della risposta al gradino unitario del
sistema retroazionato (suggerimento: utilizzare la funzione step oppure usare il modello
Simulink precedentemente sviluppato).
3. Simulazione del sistema in catena chiusa al variare del controllo proporzionale-derivativo
Considerando il solo modello semplificato, si analizzino le proprietà del sistema di controllo in
catena chiusa costituito da un controllore PD (proporzionale-derivativo) reale C(s) = Kp +
τd · s
e da una retroazione unitaria negativa. Fissando Kp = 1, per τd = 0.1, 0.5 e 0.8,
1 + 0.01s
determinare con Matlab i seguenti parametri:
1. margine di fase mϕ , margine di guadagno MG , pulsazione di taglio ωc ;
2. banda passante B3 ed eventuale picco di risonanza Mr della funzione di trasferimento ad
anello chiuso W (s);
3. tempo di salita ts ed eventuale sovraelongazione ŝ della risposta al gradino unitario del
sistema retroazionato.
2












