TORINO
MARZO 2012
COMPENDIO
DI
GEOMETRIA
Di BART VEGLIA
1
2
1
INTRODUZIONE
Il termine geometria deriva dal greco e significa misurazione della terra.
La geometria è la scienza che studia le forme e le estensioni dei corpi i quali sono
soggetti a movimenti o più in generale a trasformazioni, sul piano e nello spazio.
Nata da osservazioni empiriche e da necessità pratiche, è stata la prima disciplina cui
sono stati applicati procedimenti logico-deduttivi ad opera soprattutto di pensatori greci.
Gli strumenti principali di cui la geometria si serve sono: un mezzo per scrivere (come una
matita), una riga, una squadra,. un goniometro e un compasso.
Lo studio della geometria inizia con il metodo intuitivo. La geometria intuitiva è quella
che studia le proprietà dei corpi geometrici, alle quali dà una verifica intuitiva.
La geometria razionale, invece, basata sul metodo assiomatico-deduttivo, è quella
che, partendo da poche proprietà fondamentali della geometria intuitiva, considerate vere,
ha dedotto logicamente tutte le altre proprietà
Prima di iniziare lo studio sistematico della geometria razionale è però utile richiamare le
nozioni fondamental degli insiemi.
In seguito si studierà la geometria del piano e dello spazio.
2
2.1
INSIEMI
Concetto di insieme
Gli insiemi sono delle collezioni, raccolte, aggregati, … di elementi di qualsiasi
natura aventi caratteristiche di omogeneità
Ad es. si può parlare di: insieme di lavoratori di una azienda, di allievi di una scuola, dei
numeri naturali, delle lettere dell’alfabeto,….
I componenti degli insiemi si chiamano oggetti o elementi degli insiemi stessi.
Gli elementi degli insiemi vengono comunemente indicati con lettere minuscole; a, b,
m,…. , gli insiemi, invece, con lettere maiuscole. B, M, N
Per indicare che l’elemento a appartiene all’insieme B si scrive, simbolicamente,
a ∈ B che si legge “ a appartiene a B”
Per affermare il contrario si scrive:
a ∉ B che si legge “a non appartiene a B”
Il simbolo ∈ si chiama segno o simbolo di appartenenza.
Il simbolo ∉ si chiama segno o simbolo di non appartenenza
Per indicare che più elementi appartengono allo stesso insieme si scrive:
a, b, c ∈ N che si legge “a, b, c, appartengono ad N”
La relazione di appartenenza è caratteristica del concetto di insieme, nel senso che
per ogni ogni oggetto si deve poter stabilire se appartiene oppure non appartiene ad un
dato insieme: ovviamente la prima alternativa esclude le seconda.
Un’espressione come : “gli allievi di una certa scuola, non molto alti” non caratterizza un
insieme.
3
Per indicare qual è l’insieme di cui ci si vuole occupare si fa uso di una delle seguenti
rappresentazioni:
• Si dà l’elenco completo, racchiuso in una parentesi graffa, di tutti gli elementi
dell’insieme. Tale rappresentazione prende il nome di rappresentazione per
elencazione;
Es. B = { m, n, p, q }
•
Si enuncia una proprietà caratteristica che contradddistingue tutti gli elementi
dell’insieme.
Es. l’insieme degli allievi di una data scuola di età compresa trai 0 ed 11 anni.
2.2
Elenco degli insiemi più frequenti
Determinati insiemi, che ricorrono con maggior frequenza nello studio della matematica,
vengono contraddistinti sempre con lo stesso simbolo.
Segue un elenco di quelli più comuni
N = { 0. 1, 2, 3,….. } = insieme dei numeri naturali;
Z = {…, -2, -1, 0, +1, +2,----} = insieme dei numeri interi relativi, detto “degli interi”;
Q = {…-2,7,… -2,0,..0,...+ 5/7,... +4,8,…} = insieme dei numeri razionali relativi
detto “dei relativi” ;
Qa = { 0,…5/7,…2,…2,7, 4,8(2) …} = insieme dei numeri razionali assoluti;
R = {…-√5 ,….-4/5…0,…+√2 …} = insieme dei numeri reali relativi, detto “dei
reali”;
Ra = {0, 4/5,…√2,....7,..-.} = insieme dei numeri reali assoluti;
N0
Z0
Q0
R0
Z+
ZQ+
QR+
R--
= insiemi uguali a quelli contraddistinti dalla stessa lettera, ma senza
l’elemento zero
= insiemi uguali a quelli, contraddistinti dalla stessa lettera, relativi agli interi
relativi, positivi o negativi. (Poiché lo zero non è né positivo né negativo,
esso non appartiene ad alcuno degli insiemi di questo elenco)
R0+
R0- = insiemi dei numeri reali, positivi e negativi, incluso lo zero
2.3
Alcune definizioni
Un insieme può essere finito o infinito a seconda che l’elenco dei suoi elementi abbia o
no un termine.
Si dice singolo un insieme composto da un solo elemento, indicato con il simbolo {a}
E’ detta coppia un insieme come { a, b }
E’ detto vuoto un insieme G privo di elementi, che si indica con il simbolo G = Ø
4
Graficamente gli insiemi vengono rappresentati mediante delle
figure piane, delimitate da una linea chiusa, le qusli contengono
i simboli dei loro elementi.
Tali rappresentazioni si chiamano diagrammi di Venn,
2.4
c
a
d
b
Relazioni di uguaglianza o di equivalenza tra elementi e tra insiemi
Due elementi si dicono uguali, e si scrive a = b, se e solo se indicano un medesimo
elemento. Tale situazione viene detta relazione di uguaglianza tra elementi.
Ovviamente due elementi diversi si dicono disuguali, e si scrive a ≠ b La situazione
corrispondente dicesi relazione di disuguaglianza tra elementi.
,
La relazione di uguaglianza tra elementi gode di tre proprietà: riflessiva ( a = a ),
simmetrica ( a = b )⇒ ( b = a ) e transitiva (a = b e b = c ) ⇒ ( a = c )
Due insiemi si dicono uguali quando sono formati dai medesimi elementi, cioè sono lo
stesso insieme. Questa situazione viene detta relazione di uguaglianza tra insiemi e si
scrive A = B
La situazione opposta si dice relazione di disuguaglianza tra insiemi,e si scrive A ≠ B.
La relazione di uguaglianza tra insiemi gode delle stesse proprietà elencate prima
per gli elementi
2.5
Sottoinsiemi – Relazione di inclusione
Dati due insiemi A e B non uguali, se ogni elemento
di B è anche elemento di A, si dice che B è un
sottoinsieme di A o che B è contenuto o incluso
B ⊂ A
in A e si scrive
B
A
La suddetta scrittura e la relativa situazione prendono il nome di relazione di inclusione
tra insiemi ed il simbolo ⊂ si chiama segno o simbolo di inclusione.
Ad es l’insieme dei numeri pari è un sottoinsieme dell’insieme dei numeri naturali
La relazione di inclusione tra insiemi gode delle tre
seguenti proprietà: riflessiva(B ⊂ B), transitiva
(A ⊂ B e B ⊂ C) ⇒ (A ⊂ C) (V. figura a fianco)
e antisimmetrica (A ⊂ B e B ⊂ A) ⇒ (A = B)
2.6
A
B
Operazioni con gli insiemi
Dati due insiemi A e B, si dice insieme intersezione o, semplicemente,
intersezione, l’insieme degli elementi che appartengono sia ad A che a B
5
C
si scrive, simbolicamente A ∩ B, che si legge
A intersezione con B, oppure A intersecato
con B (In figura la zona di colore arancio)
Il simbolo ∩ è detto segno o simbolo di intersezione.
A
B
A ∩ B
Due insiemi, A e B, privi di elementi comuni si
dicono disgiunti.
Dati due insiemi, M e N, si dice insieme unione o riunione dei due insiemi l’insieme
degli elementi che appartengono, indifferentemente, ad almeno uno dei due insiemi e si
scrive M ∪ N, che si legge M unione N,
oppure M unito con N. (In figura: l’insieme
M
M ∩ N è quello a contorno rosso, mentre
N
quello a contorno verde è l’insieme M ∪ N)
Il simbolo ∪ si chiama segno o simbolo
M ∪ N
M ∩ N
di unione.
Dato un insieme P, due suoi sottoinsiemi A e B tali che A ∩ B = Ø e A ∪ B = M
si dicono complementari.
La differenza di due dati insiemi: A e il
suo sottoinsieme B, ( presi nell’ordine ) è
l’insieme formato dagli elementi di A
non appartenenti a B e si scrive A - B
(In figura è la zona colorata in rosa)
2.7
A
B
A-B
Insieme delle parti
Se A, B, C…. sono dei sottoinsiemi di M, cioè A, B, C,… ⊂ M, potendo decidere se
A = B oppure A ≠ B, tali sottoinsiemi si possono considerare come degli elementi di un
nuovo insieme detto insieme delle parti di M, che si indica con P (M)
Cioè: l’insieme delle parti P (M) di un insieme M è l’insieme che ha come elementi
i sottoinsiemi di M
2.8
Coppie ordinate
Dati due insiemi, un primo A ed un secondo B, non vuoti, se a, a1… sono elementi di A
e b, b1…elementi di B, l’espressione (a; b) dicesi coppia ordinata di cui a è il primo
componente o elemento e b il secondo componente della coppia.
Due di questi oggetti sono uguali (a, b) = (a1, b1) se e solo se a = a1 e b = b1
2.9
Prodotto cartesiano
Le coppie ordinate come (a, b), (a1, b1) ,…formate dagli elementi degli insiemi A e B
possono costituire un nuovo insieme, detto prodotto cartesiano degli insiemi A e B
che si scrive A x B. Dunque
6
(a ∈ A, b ∈ B) ⇔ [ (a, b) ∈ A x B]
Se il secondo insieme è uguale al primo cioè B = A fra le coppie ordinate, cioè fra gli
elementi di A x A figurano anche quelle del tipo (a, a) (b ,b)…..
In simboli, se M = { x,y,z} ed N = {1, 2, 3} si può scrivere:
M x N = { (x, 1), (x, 2), (x, 3), (y, 1), (y, 2), (y, 3), (z, 1), (z, 2), (z, 3)}
Poiché normalmente è (x, y) ≠ (y, x) è pure M x N ≠ N x M.
Se i due insiemi A e B sono uguali il prodotto cartesiano
2.10
A x B si scrive A x A = A2
Relazioni tra gli elementi di un insieme
Data la coppia ordinata (m; n) di un insieme, non vuoto, A, se una certa proprietà R, che
può essere vera o falsa, è vera per la coppia data, si dice che gli elementi m ed n,
presi nell’ordine, soddisfano la proprietà R, che viene detta relazione binaria e si
scrive
mRn
Tale relazione gode delle proprietà: riflessiva, simmetrica, transitiva e antisimmetrica,
che sono già state esaminate ai §§ 2.4 e 2.5
2.11
Corrispondenze tra insiemi
Una relazione f fra due insiemi A e B, che associ ad ogni x ∈ A uno ed un solo
y ∈ B si chiama corrispondenza univoca o mappa o applicazione di A in B e si
scrive f: A ⇒ B
La coppia ordinata (x, y) è detta coppia di elementi corrispondenti della f e si scrive
y = f(x) che si legge y è il corrispondente di x o, anche, y è una lmmagine di x
oppure ancora, (x, y) sono una coppia di elementi corrispondenti, nella mappa f.
Es. 1) A è un insieme di figli e B quello dei rispettivi padri. La relazione x
una mappa f : A ⇒ B
∈Α
Es. 2) A è un insieme di mariti e B quello delle rispettive mogli. La relazione x
è una mappa f : A ⇒ B
2.12
ha per padre y
∈Α
∈
ha per moglie y
B è
∈
B
Corrispondenze biunivoche
Se nella corrispondenza y = f(x) non soltanto, ad ogni elemento di A corrisponde un
elemento di B ma anche, viceversa, ogni elemento di B è il corrispondente di un solo
elemento di A, si dice che f è una corrispondenza biunivoca o una mappa biiettiva
o una applicazione biiettiva tra A e B e si scrive A ⇔ B
Ad es. Nell’es 1) del precedente § la f non è biunivoca perché un padre può avere più di un figlio.
Nell’es 2) “
“
“ la f è biunivoca
2.13
Corrispondenza inversa
Se f è biunivoca, oltre alla mappa di A su B esiste pure una mappa di B su A che
viene detta mappa o corrispondenza inversa della f, che si indica con il simbolo
7
f -1: B ⇒ A
Un esempio di corrispondenza inversa
-1
La corrispondenza inversa di f : y = x + 1 è f : x = y – 1
L’addizione, la moltiplicazione e l’innalzamento al quadrato sono corrispondenxe dirette.
La sottrazione, la divisione e l’estrazione della radice quadrata sono corrispondenze inverse
2.14
Corrispondenza di Talete
s’
In un piano è dato un fascio di rette parallele tagliate da
due trasversali, s ed s’. Le rette del fascio stabiliscono
una corrispondenza biunivoca tra le rette trasversali
f: s → s’ in cui ai punti A, B, ecc ( sulla retta s e,
rispettivamente, sulle parallele a, b, ecc) corrispondono
i punti A’ (sulla a), B’ (sulla b), ecc, tutti sulla s’,
Questa corrispondenza non è che la proiezione parallela
dei punti della s sulla s‘ e, come si vedrà, iriveste una
notevole importanza in Geometria, in cui è nota come
corrispondenza parallela di Talete.
Analogamente, se le rette s ed s’ sono parallele ed il
punto S, centro di un fascio proprio, non appartiene
ad alcuna di esse, le rette del fascio proprio stabiliscono
una corrispondenza biunivoca tra s ed s’ f : s → s’
in cui, se ad es., B e B’ stanno sulla stessa retta b del
fascio, a B corrisponde B’.
e
s
E’
E
D ≡ D’
d
c
C
b
a
C’
B
B’
A
A’
s
s’
b
S
s’
s
A
A’
a
P’
B’
P
B
Anche questa corrispondenza ha una notevole importanza
in Geometria e si chiama corrispondenza centrale di Talete.
2.15
Composizione di mappe
Date due mappe f : A ⇒ B
e
g: B⇒ C
risulta definita una terza mappa
f :
A ⇒ C
che si dice ottenuta mediante
composizione delle mappe y = f(x) e
z = g(y)
che danno z = g o f(x)
indicando con g o f la mappa composta h
La composizione di mappe si può anche chiamare prodotto operatorio o, più
semplicemente, moltiplicazione
Es. Sia A è l’insieme degli allievi che fanno una prova scritta, B l’insieme di queste prove, C l’insieme
dei voti. y = f(x) associ ad ogni allievo x la sua prova scritta y; z = g(y) associ ad ogni prova scritta y il
relativo voto z. Allora la mappa composta z = g(f(x)) = g o f(x) associa ad ogni allievo x il voto ottenuto z
2.16
Elementi uniti di una corrispondenza. - Identità
Data la mappa y = f(x) sopra un insieme A f: A ⇒ A si dice che a ∈ A è un
elemento unito o fisso della mappa f se a = f(a)
8
Fra le corrispondenze sopra un insieme A si considera l’identità I che è la
corrispondenza nella quale sono uniti (o fissi) tutti gli elementi dell’insieme stesso.
2.17
Corrispondenze involutorie.
Data la corrispondenza f: y = -x
e la sua inversa
f -1:
z = -y le due
corrispondenze coincidono:infatti in esse a ogni numero intero corrisponde il proprio
opposto
Una corrispondenza che gode di questa proprietà dicesi involutoria.
Si può quindi affermare: una corrispondenza involutoria coincide con la propria
inversa f = f -1
2.18
Partizione di un insieme e sue proprietà.
La partizione F di un insieme M è la suddivisione dell’insieme dato in un numero,
finito od infinito, di sottoinsiemi A, B, C, … detti classi della partizione di M, che
godono delle seguenti proprietà:
a) nessuna delle classi è vuota;
b) due classi qualunque sono disgiunte, cioè prive di elementi comuni ( v. § 2.6);
c) la riunione delle classi è l’insieme M, cioè A ∪ B ∪ C ∪…..
Si può anche dire che: più sottoinsiemi, non vuoti, A, B, C
di un insieme M costituiscono una partizione di M se ogni
A
D
elemento di M appartiene ad uno ed uno solo di questi
sottoinsiemi. (In figura è rappresentata una partizione
B
C
dell’insieme M in quattro classi )
M
Stabilita una partizione F di M, un elemento x ∈ M individua la classe di F cui
appartiene. Esso viene chiamato rappresentante della classe e lo di indica con il simbolo
[ x ] Quindi se a e a’ appartengono ad una stessa classe, per es. A, della partizione,
si ha
[ a ] = [ a’]] = A
Al § 2.7 si era visto che i sottoinsiemi di un insieme M possono essere considerati come
gli elementi dell’insieme delle parti di M P(M)
Se dunque le classi della partizione F: [ a ] = A, [ b ] = B, [ c ] = C…..vengono
considerate come elementi, esse costituiscono un nuovo insieme, indicato ancora con F
Es. Gli abitanti della Svizzera appartenenti ad un insieme M dicono che la loro lingua è: Tedesco = t,
.
Francese = f, Italiano = i Si ha così una partizione F di M costituita dai tre sottoinsiemi dei
.
Tedeschi, dei Francesi e degli Italiani, che si possono interpretare come elementi dell’insieme F = {t,f,i}
2.19 Relazione di equivalenza – Insieme quozien
i un insieme M ed una sua partizione F, si dice che due elementi
x, x’ ∈ M
sonoivalenti nella partizione F e si scrive
x ∼ x’, se essi appartengono ad una
medesima classe di F.
Ad es. nella partizione in classi del’insieme allievi di una scuola, sono equivalenti due allievi della stessa
classe
[relazione di equivalenza sopra definita si dice associata alla
partizione F. Due elementi equivalenti sono detti rappresentanti di una medesima
9
classe della partizione.Quindi per quanto detto al precedente §:lla relazione di
equivalenza fra due elementi, x ∼ x’, segue la relazione di uguaglianza fra classi [x]] = [
x’]] e viceversa
Ne con relazione di equivalenza fra elementi gode dellroprieta
della zione di uguaglianza, che sono: la riflessiva, la simmetrica, la transitiva.
Si conviene quindi di chiamare relazione di equivalenza E fra elementi di un insieme
ogni relazione che gode delle suddette proprietà.
Conviene verificare subito la proprietà fondamentale che collega questa definizione con
quella precedente.
Ogni relazione di equivalenza E fra gli elementi di un insieme M è associata ad
una partizione F di M
Infatti, dato un x ∈ M si prendono in considerazione tutti gli x’ ∈ M, equivalenti ad x
nella suddetta relazione di equivalenza E e si conviene di indicare questa classe con [x]].
Innanzitutto si osserva che essa non è vuota poiché da x ∼ x’ segue x ∈ [ x ].
Inoltre due elementi qualunque x’ ed x’’, appartenenti entrambi alla stessa classe [x]],
sono tra loro equivalenti.
(x’, x’’ ∈ [ x ] ) ⇒ ( x’ ∼ x’’)
Infatti da x’ ∼ x, x’’ ∼ x, da cui x’ ∼ x, x ∼ x’, deriva x’ ∼ x’’.
Per questo la classe [ x ] è detta una classe di equivalenza e
(1)
x ∼ x’ ⇒ [ x ] = [ x’ ]
Infatti ognii elemento della classe [ x ] ( poiché è equivalente ad x che è equivalente ad
x’) , è anche equivalente ad x’, cioè appartiene a [ x’ ], per cui [ x ] ⊂ [ x’]].
In modo simmetrico è [ x’]] ⊂ [ x ].
E’ quindi dimostrata l’affermazione fatta poco sopra relativa alla relazione di equivalenza
fra elementi, da cui segue quella fra classi
Si può anche facilmente constatare che due classi di equivalenza sono disgiunte, ossia
due classi di equivalenza, aventi un elemento in comune, coincidono.
Infatti da z ∈ [x]] , z ∈ [y]] deriva z ∼ x, z ∼ y e per la (1)
[z]] = [x]], [z]] = [y]] quindi [x]] = [y]]
Le proprietà prima esaminate si possono riassumere mediante il seguente principio di
contrazione, detto anche passaggio al quoziente:
Se in un insieme M è data una relazione di equivalenza E, gli elementi di M si
suddividono in classi di equivalenza che costituiscono una partizione di M.
Queste classi si possono interpretare come elementi di un nuovo insieme F
( x, x’ ∈ M ) ⇔ ( [x]], [x’]] ∈ F)
tali che
x ∼ x’ ⇔ ([[x]] = [x’]])
Es. Sia M = {a, b, c,…} l’insieme dei numeri interi relativi. Stabiliamo che due interi a , b sono
equivalenti se
a – b = 2n
con n numero intero qualsiasi (incluso lo zero)
Si può verificare facilmente che si tratta effettivamente di una relazione di equivalenza, che dà luogo a
due sole classi di equivalenza [0]]. e [1]], quella dei numeri pari e quella dei numeri dispari.
Infatti prendendo ad es. n = 3 cioè 2n = 6 con dei numeri pari si può scrivere 10 – 4 = 6; 12 – 6 = 6,
-2 +8 = 6 e con dei numeri dispari 13 – 7 = 6; 31 - 25 = 6; -13 + 19 = 6
2.20
Relazione d’ordine
10
Un insieme M dicesi (totalmente) ordinato se fra i suoi elementi intercede una
relazione che si scrive x < y e si legge “x minore di y” oppure “ x precede y ” , tale
che
1) ( x < y e y < z) ⇒ ( x < z) che è la proprietà detta Transitiva della relazione ordinale:
2) tra due elementi qualunque di M sussiste una ed una sola fra le seguenti tre
relazioni: x = y o x < y o y < x che è la proprietà detta di Tricotomia.
Un insieme M dicesi parzialmente ordinato se fra i suoi elementi sussiste una relazione
x < y tale che:
1 ) ( x < y e y < z) ⇒ ( x < z) che è la proprietà Tansitiva, come al precedente punto 1
2) tra due elementi qualunque di M sussiste al più una delle seguenti tre relazioni:
x=y o x<y o y<x
Le suddette relazioni d’ordine vengono solitamente chiamate relazioni di ordine stretto
per il fatto che x < y ⇒ x ≠ y
Una relazione d’ordine non stretto, indicata con “ x ≤ y “, aggiunge le coppie del tipo
(x, x)
2.21
Proprietà degli ordinamenti totali
Se in un insieme ordinato M esiste un elemento maggiore di tutti gli altri, detto massimo;
minore di tutti gli altri, detto minimo, è evidente che:
1) Un insieme ordinato può avere un solo massimo od un solo minimo;
2) Un insieme ordinato e finito è sempre dotato di massimo e di minimo.
Un insieme ordinato senza né massimo né minimo,si dice illimitato
Ogni x ∈ M, tale che a < x < b (oppure b < x < a) dicesi compreso tra i due
elementi.
Ogni insieme ordinato M si dice denso se fra due suoi elementi distinti è srmpre
compreso un altro elemento di M.
Quindi: Se M è un insieme (ordinato) denso, fra due suoi elementi distiìnti
qualunque sono compresi infiniti elementi di M2.22
Operazioni e strutture algebriche - Legge di composizione
Se si indica con N l’ insieme dei numeri naturali a, b, c,…(zero incluso), l’addizione dei
naturali a + b = c può essere considerata una coppia ordinata (a, b) di elementi di N
che associa un elemento c di N.
Questa operazione è quindi una mappa g : N x N ⇒ N
ordinate dei naturali nell’insieme dei naturali stessi.
dell’insieme delle coppie
Così pure la moltiplicazione dei naturali è una nuova mappa h: N x N ⇒ N
Dai suddetti esempi nasce la seguente definizione astratta di operazione:
11
Dato un insieme non vuoto E, dicesi operazione (oppure legge di composizione in
E) una mappa f : E x E ⇒ E
Questa mappa associa ad ogni coppia ordinata (a, b) di elementi di E un certo
elemento c, sempre di E
(a, b) ⇒ c detto risultato dell’operazione.
Se l’operazione si chiama addizione o moltiplicazione il risultato si indica,
rispettivamente, con la notazione additiva c = a + b, oppure moltiplicativa c = ab.
2.23
Monoidi
Nella geometria elementare è particolarmente importante una struttura additiva M , la cui
operazione è associativa, ossia, per ogni terna di elementi di M è
(a+b)+c = a+(b+c)
Se in M esiste un elemento z tale che, per ogni a ∈ M si abbia a + z = z + a = a
tale elemento è detto elemento neutro o identico per l’operazione considerata.
Se tale operazione è l’addizione l’elemento neutro è lo zero e lo si indica con 0.
E’ evidente che M può avere un solo elemento neutro.
Una struttura algebrica con una operazione associativa e dotata di un elemento neutro si
dice monoide che è additivo o moltiplicativo a seconda che la legge di composizione sia
l’addizione o la moltiplicazione.
Il monoide additivo M è un insieme M tale che, per elementi a, b, c, qualunque, di M
è
1) (a + b) = s
(esistenza dell’operazione)
2) (a + b) + c = a + (b + c)
(associatività)
3) a + 0 = 0 + a = a
(esistenza dello zero)
Se la legge di composizione di M è commutativa e cioè per ogni coppia di elementi di M
è
a+b = b+a
il monoide si dice commutativo o abeliano.
Un elemento a di un monoide dicesi regolare o cancellabile (da cui la legge di
cancellazione) se (a + x = a + y) ⇒ x = y per ogni x, y ∈ M.
Un monoide nel quale ogni elemento è regolare dicesi monoide regolare.
Esempio L’insieme dei nmeri naturali non nulli N0 rispetto alla moltiplicazione, è un monoide abeliano il cui
elemento neutro si chiama elemento unità ed è il numero 1
a•1 = 1 • a = a
per ogni a ∈ N0 e regolare
Invece la struttura moltiplicativa di tutti i naturali è un monoide (moltiplicativo) abeliano ma non regolare dato
che non è regolare l’elemento zero; cioè non è vero che
0 • x = 0 • y ⇒ x = y per ogni x, y ∈ N
2.24
Gruppi
Dato un monoide G, ad es. moltiplicativo, il suo elemento unità si indica con il
simbolo 1.
Se, dato un a ∈ G, esiste un a’ ∈ G tale che a a’ = a’ a = 1 a’ è detto
elemento simmetrico o reciproco o inverso di a e si indica con a-1
Un elemento dotato di simmetrico si dice simmetrizzabile.
L’elemento simmetrico di 1 è ancora l’elemento identico 1.
12
Esistono monoidi nei quali ogni elemento è simmetrizzabile: essi si chiamano gruppi e la
loro legge di composizione si dice generalmente moltiplicazione e si indica con un • o
anche niente .In tal caso il gruppo si dice moltiplicativo.
L’elemento identico, oltrechè con 1 si può indicare con e.
Un gruppo moltiplicativo G è un insieme, dotato di operazione moltiplicazione, tale che
per elementi a, b, c,… qualunque di G è
1) (a b) c = a (b c)
(proprietà associativa)
2) e a = a e = a
(esistenza dell’elemento identico o unità)
3) a-1 a = a a-1 = e
(esistenza dell’elemento simmetrico)
4) a b = b a
(proprietà commutativa); se questa proprietà vale, il gruppo è abeliano
Talvolta la legge di composizione di un gruppo si chiama addizione. In questo caso il
gruppo si dice additivo.
L’elemento unito dicesi zero e si indica con 0.
Il gruppo simmetrico di a è -a (opposto di a) e quindi la precedente proprietà 3)
diventa:
3’ ) -a + a = a + (-a) = 0
Un gruppo additivo è un monoide additivo in cui ogni monoide è dotato di opposto.
Si prendono ora in considerazione alcune fondamentali proprietà dei gruppi.
1°) Un gruppo è dotato di un solo elemento unità.
2°) In un gruppoo vale la legge di cancellazione, cioè ogni elemento è regolare
ax = ay ⇒ x = y
xa = ya ⇒ x = y
3°) In un gruppo ogni elemento ammette un solo si mmetrico
Un gruppo che possiede un numero finito di elementi si dice gruppo finito.
2,25
Sottoinsieme stabile – Sottogruppi
Se ad es. si considera il monoide additivo N dei numeri naturali ed il suo sottoinsieme P
a, b ∈ P ⇒ a + b ∈ P
dei numeri pari (zero incluso: P ⊂ N), si ha
Il che significa che la somma di due numeri pari è ancora un numero pari. Si dice perciò
che P è un sottoinsieme stabile del monoide additivo N.
Si definisce quindi stabile un sottoinsieme (non vuoto) A di un monoide additivo M tale
che per ogni coppia a, b di elementi di A si abbia a + b ∈ A.
Se M è un monoide il suo sottoinsieme stabile si dice sottomonoide di M, purché
contenga l’elemento neutro di M.
Con riferimento all’esempio precedente, il sottoinsieme P dei numeri naturali pari (zero
incluso) è un sottomonoide del monoide additivo N dei numeri naturali.
Invece l’insieme dei numeri pari (zero escluso) è solo un insieme stabile di N.
Il sottoinsieme P dei numeri pari è stabile anche per il monoide moltiplicativo dei
naturali, ma non è un sottomonoide.
Invece il sottoinsieme D dei numeri naturali dispari è stabile per il monoide
moltiplicativo N, di cui è un sottomonoide, ma non è stabile per il monoide additivo N.
13
Un sottomonoide stabile H di un gruppo G dicesi sottogruppo di G.
Perché H sia un sottogruppo di un gruppo (moltiplicativo) G, deve soddisfare alle seguenti
condizioni:
1) a, b ∈ H ⇒ ab ∈ H
2) e ∈ H
3) a ∈ H ⇒ a-1 ∈ H
Non è citata la proprietà associativa perché, essendo essa valida in G, lo è anche nel
sottoinsieme stabile H.
14
3
3.1
GEOMETRIA NEL PIANO
Definizioni
Come in ogni disciplina anche in geometria è necessario dare delle definizioni che
servono ad indiduare in modo chiaro e sicuro un oggetto geometrico o un concetto o una
proprietà.
Una definizione però deve necessariamente fare uso di qualche termine che si suppone
noto.
A es. definendo il segmento come “parte di una retta compreso tra due punti” si usano i
concetti di retta e di punto, che si suppone siano conosciuti da chi legge tale definizione.
3.2
Enti primitivi
In geometria si suppongono noti i termini: punto, retta, e piano che sono i termini o
concetti primitivi. Non è invece primitivo il concetto di spazio che può essere definito
come l’insieme di infiniti punti.
Un punto può essere rappresentato graficamente con il segno lasciato dalla punta di una
matita su un foglio di carta.
Una retta è rappresentata dalla traccia di una matita, che scorre lungo una riga, imitando
la forma di un filo sottile ben teso.
Il piano è rappresentato da un foglio di carta ben disteso in tutte le direzioni.
Nella trattazione della geometria i punti vengono solitamente indicati con le lettere
maiuscole dell’alfabeto, le rette con le lettere minuscole ed i piani con le lettere minuscole
dell’alfabeto greco.
3.3
Assiomi o postulati
Le proposizioni fondamentali della geometria intuitiva, cui si è accennato nella
Introduzione, hanno il nome di assiomi o postulati. Essi , accettati per veri a priori,
riguardano gli enti primitivi tra i quali esistono delle relazioni di appartenenza e di
uguaglianza, dette relazioni primitive.
3.4
Alcuni assiomi fondamentali
Sono fondamentali i seguenti assiomi:
a) Due punti, A e B, distinti, nello spazio, appartengono ad una sola retta.
b) Tre punti non allineati appartengono ad un solo piano.
c) Per un punto passano infinite rette.
d) Se due punti di una retta appartengono ad un piano, la retta giace su tale piano.
e) Il piano è un insieme di infiniti punti e di infinite rette.
f) Lo spazio contiene infiniti punti, infiniti piani ed infinite rette.
3.5
IPOTESI, TESI, DIMOSTRAZIONE, TEOREMA
Ogni proprietà diventa vera se si può dedurre in modo logico, ossia con il ragionamento,
dagli assiomi e prende il nome di teorema.
15
Ogni teorema è costituito da una ipotesi che è la verità di una prima proprietà, da cui si
deduce mediante un ragionamento, detto dimostrazione, una seconda proprietà, detta
tesi.
SI dice che l’ipotesi (P1) implica la tesi (P2) e, simbolicamente si scrive P1 ⇒ P2 .
Se in un teorema le proprietà sono tali che anche la seconda implica la prima, esse si
dicono equivalenti e si scrive in simboli
P1 ⇔ P2 in cui il simbolo ⇔ è detto
simbolo di equivalenza logica.
Si dice che la verità dell’ipotesi è sufficiente per la verità della tesi e che la verità della
tesi è necessaria per quella dell’ipotesi (infatti se la tesi non fosse vera non potrebbe
esserlo nemmeno l’ipotesi) .
Se le due proprietà sono equivalenti la verità dell’una è necessaria e sufficiente per
quella dell’altra.
Il teorema cui corrisponde il simbolo P1 ⇒ P2 . si chiama teorema diretto, mentre quello
con il simbolo P2 ⇒ P1 è detto teorema inverso. Se entrambi tali teoremi sono validi le
due proprietà sono equivalenti.
Ad es. L’ipotesi “ Una figura piana con quattro angoli (quadrtangolo) ha quattro angoli retti” implica la tesi
“ Le sue diagonali sono uguali”. La prima affermazione è sufficiente per confermare la seconda, per cui si
può affermare che se le diagonali non sono uguali il quadrangolo non può essere un rettangolo. Cioè
condizione necessaria perché un quadrangolo sia un rettangolo è che le sue diagonali siano uguali.
Ma questa condizione non è sufficiente perché, ad es., un trapezio isoscele ha le due diagonali uguali ma
non è un rettangolo.
3.6
COROLLARI
I teoremi che sono un’immediata conseguenza di un altro teorema o di un assioma si
dicono corollari
3.7
LE FIGURE GEOMETRICHE
In base alle nozioni introdotte si possono ora prendere in considerazione i vari enti che
fanno parte della geometria, che sono le figure geometriche.
Una figura geometrica è un qualunque sottoinsieme, non vuoto, di punti.
In questa parte della trattazione, dedicata alla geometria piana o planimetria, si
considerano solo le figure geometriche giacenti su un piano.
3.8
LA CONGRUENZA
In geometria occorre distinguere tra uguaglianza e congruenza tra figure geometriche.
Due figure sono uguali se sono perfettamente coincidenti; sono congruenti se hanno
forme e dimensioni uguali ma occupano spazi diversi.
Due punti congruenti si dicono corrispondenti od omologhi.
Ad es. in un triangolo equilatero i tre lati si dicono congruenti tra loro, e non uguali perché
non coincidono, pur avendo la stessa lunghezza. Considerando invece uno dei tre lati, ad
es. BC, dello stesso triangolo, si può dire che l’altezza, la mediana e la bisettrice ad esso
relative AH (dei termini suddetti verranno date le definizioni in seguito), sono uguali
perché coincidono esattamente.
A
16
C
H
B
3.9
LA RETTA E LE SUE PROPRIETA’
Una retta si può rappresentare facendo scorrere la punta di una matita lungo il bordo di
una riga.
La retta però non è limitata alla lunghezza della riga ma è formata da infiniti punti, cioè è
illimitata.
Si è già detto, elencando alcuni esempi di assiomi (v. § 3.4) che per un punto passano
infinite rette.
Così pure si è detto che per due punti passa una sola retta.
Tre punti di una stessa retta si dicono allineati.
Due rette aventi un punto in comune si dicono incidenti o secanti ed il punto comune è
detto intersezione.
Le infinite rette che passano per un punto, A,
costituiscono un fascio proprio di cui il punto
A viene detto sostegno.
3.10
A
La retta orientata
Una retta può essere immaginariamente percorsa in due sensi e si può quindi affermare
che una retta è dotata di due sensi o versi, uno opposto all’altro, detti: l’uno positivo,,
l’altro negativo. Se sulla retta si fissano due punti, A e B, di cui il primo a sinistra del
secondo, si può stabilire, ad es., che il verso positivo della retta è quello da A verso B.
Se su una retta viene fissato un verso positivo si dice che la retta è orientata e su di essa
si fissa un punto, O che è chiamato origine.
•
I punti a destra di O si possono immaginare
corrispondenti ai numeri positivj, quelli alla
O
+
sinistra ai numeri negativi.
3.11
Le semirette
Data una retta, se su di essa si prende un qualsiasi punto A , tale punto divide la retta in
due parti, dette semirette di cui A è l’origine. Tali semirette sono opposte e l’una è il
prolungamento dell’altra.
3.12
Il segmento
Se su una retta, anziché un solo punto se ne prendono due, distinti, A e B, essi
delimitano una parte di retta detta segmento di cui A e B sono gli estremi.
Esso viene simbolicamente indicato con AB, o meglio, con AB.
In figura sono rappresentati, su una retta a, il
a
•
•
segmento AB e due semirette, una con l’origine
A
B
in A e l’altra con l’origine in B.
3.13
Confronto tra due segmenti
Per stabilire se due segmenti AB e CD sono tra loro congruenti è necessario
confrontarli.
17
Per effettuare questo confronto bisogna trasportare uno dei segmenti e sovrapporlo
all’altro in modo che un estremo dell’uno coincida con un estremo dell’altro.Questa
operazione di trasporto di un segmento si puo, ad es., effettuare mediante un compasso a
punte fisse che viene aperto in modo che le due punte coincidano con gli estremi del
segmento che si intende trasportare, ad es. AB e poi, senza variare l’apertura del
compasso, si fa coincidere una delle punte con un estremo, ad es C, dell’altro segmento.
Per quanto riguarda l’altra punta del compasso
si possono verificare tre casi:
1°) l’altra punta coincide esattamente con
il secondo estremo del segmento sul quale si
A
B
vuole effettuare il confronto: in tal caso i due
C
D
segmenti sono congruenti, cioè è AB ≅ CD;
2°) l’altra punta del compasso capita tra C
A
B
e D: in questo caso il segmento AB è
C
D
minore di CD: cioè è AB < CD;,
3°) l’altra punta del compasso cade sulla retta
CD, oltre il punto D, nel qual caso AB risulta
A
B
maggiore di CD, cioè è AB > CD.
C
D
3.14 Somma di due o più segmenti
Si chiama somma o addizione di due segmenti adiacenti, AB e CD, il segmento AC
e si scrive AB + BC = AC.
I due segmenti da sommare si chiamano addendi.
Il segmento AC è il segmento unione dei due addendi, A
B
C
cioè il segmento avente per estremi gli estremi non comuni dei segmenti dati.
Se i due segmenti non sono adiacenti, come ad es.
LM e PQ, si rendono tali traportando (v § precedente)
su una semiretta di origine L’ il segmento L’M’ ≅ LM
e di seguito, il segmento adiacente P’Q’ ≅ PQ.
P' coincide con M’.
Il segmento L’Q’ è la somma dei due segmenti dati.
M
P
L
Q
L’
M’
Se i segmenti sono tre o più, con il metodo sopra
descritto si aggiunge il terzo segmento ed
P’
Q’
eventualmente i successivi, alla somma dei primi
due. L’ultimo segmento ottenuto, compreso fra il primo estremo del primo ed il secondo
estremo dell’ultimo, è il segmento somma dei segmenti dati.
3.15
Proprietà della somma di segmenti
La somma di due segmenti gode delle stesse proprietà della somma di due numeri
naturali. Esse sono:
Proprietà commutativa La somma di due segmenti, AB e CD, non cambia se si
cambia l’ordine degli addendi. AB + CD = CD + AB
Proprietà associativa La somma di tre o più segmenti non cambia se a due o più di
essi si sostituisce la loro somma. AB+CD+EF = AB+(CD+EF)
18
3.16
Multipli e sottomultipli di un segmento
Dato un segmento AB, il segmento CD, uguale alla somma di due o pIù (ad es. 3 come
in figura) segmenti congruentii ad AB, si dice
multiplo di AB e si scrive CD = 3 AB
A
B
A sua volta il segmento AB risulta la terza
C
D
parte di CD e si scrive AB = 1/3 CD.
In questo caso il segmento AB è un sottomultiplo di CD
3.17
Differenza tra due segmenti
Dati due segmenti, MN e RS, con MN > RS, se, come è stato descritto per la somma,
si sovrappone il più corto, RS, sull’altro in modo che l’estremo R dell’uno coincida con
l’estremo M dell’altro, il segmento SN è la differenza
o sottrazione fra i segmenti MN ed RS e si scrive
R
S
MN – RS = SN
Si può quindi dire che la differenza tra due segmenti
M
N
diseguali è il segmento che si deve sommare al minore per ottenere il maggiore.
B
3.18 Distanza tra due punti - Spezzata
A
Dati due punti, A e B, il segmento AB che li congiunge
C
D
rappresenta il più breve cammino fra di essi. Infatti se si considera la spezzata, ACDB,
cioè la somma di più segmenti, complanari ma non appartenenti alla stessa retta, che ne
costituisco i lati, la loro somma è senza dubbio maggiore del segmento AB, che li
congiunge e che viene detto distanza tra i due punti.
3.19
Punto medio di un segmento
R
S
Se un segmento MN è il doppio del segmento RS,
il punto P, che divide il segmento MN in due parti
M
P
congrunti, tale che RP ≅ PN ≅ RS, si chiama punto medio del segmento MN.
3.20
N
IL PIANO E LE SUE PROPRIETÀ
Dopo il punto e la retta, il piano è il terzo elemento fondamentale della planimetria.
Esso può essere rappresentato da un foglio di carta ben teso, dalla lastra di una lavagna,
dalla plancia di un tavolo ,che devono però essere immaginati senza spessore ed
infinitamente estesi.
Il piano contiene infiniti punti ed infinite rette.
La retta che passa per due punti di un piano giace interamente sul piano.
Punti e rette appartenenti allo stesso piano si dicono complanari.
3.21
Il semipiano
semipiano
Una retta a posta su un piano lo divide
in due semipiani di cui la retta è il bordo
o l’orlo o il contorno o l’origine o la
frontiera.
a
semipiano
19
I due semipiani sono uno opposto all’altro.
Ogni segmento AB i cui estremi stanno
sui semipiani opposti, giace parte su uno
e parte sull’altro, attraversando la frontiera
in un punto C.
3.22
B
semipiano
C
A
a
semipiano
LA CIRCONFERENZA E LE SUE PARTI
Una linea chiusa che ha una notevole importanza in geometria è la circonferenza, che si
realizza graficamente mediante un compasso.
La circonferenza può essere definita come l’insieme dei punti di un piano ugualmente
distanti da un punto fisso O detto centro.
N
I segmenti come OA ed OB, tra loro congruenti,
d
che congiungono il centro con un qualsiasi
punto della circonferenza, si chiamano raggi, r
O
r
Una circonferenza viene comunemente indicata
B
mediante il centro ed il raggio.
A M
Un qualsiasi segmento come ad es. AB, che collega due punti della circonferenza, si dice
corda. Le infinite corde che passano per il centro si chiamano diametri, d
I due punti A e B dividono la circonferenza in due parti, detti archi.
Per contraddistinguere un arco si usa segnare tra i due estremi dell’arco stesso una
lettera, ad es, M, e l’arco corrispondente, se i suoi estremi sono A e B, può essere
indicato con AMB. L’altro arco, ovviamente, è quello BNA. Naturalmente una
circonferenza può essere divisa in più di due archi da molti punti su di essa.
3,23
L’ANGOLO
La parte di piano compresa tra due semirette a e b, aventi la stessa origine V, è un
angolo, che viene solitamente indicato con una lettera greca minuscola. Le due semirette
si chiamano lati dell’angolo ed il punto V, origine del lati, è detto vertice.
3.24
Angoli concavi ed angoli convessi
In realtà gli angoli formati dalle due semirette sono
due: di cui uno, β che contiene i prolungamenti dei
lati (tratteggiati), è detto concavo, mentre l’altro, α
che non contiene i prolungamenti, dei lati è detto
convesso.
β
3.25
α
Angolo piatto e angolo giro
Se le due semirette che costituiscono i lati di un angolo
giacciono sulla medesima retta, i due angoli, congruenti,
da esse formati, si chiamano angoli piatti indicati con
il simbolo π
Se, invece, le due semirette coincidono, l’angolo è
uno solo e si chiama angolo giro.
20
π
π
π V
3.26
Angoli consecutivi, adiacenti e opposti al vertice
Due angoli α e β, sullo stesso piano, si definiscono
consecutivi se hanno in comune il vertice ed un lato.
Due angoli, come sopra, si definiscono adiacenti se
la loro somma è un angolo piatto.
V
α
a
β
b
c
α
Due angoli, come sopra, si definiscono opposti al
vertice se i lati di uno sono i prolungamenti dei lati
dell’altro. Essi sono congruentii: α ≅ β α
Sono pure opposti al vertice i due angoli adiacenti
ad α ed a β.
β
β
V
α
3.27
Trasporto di un angolo – Angoli uguali
b
Per trasportare un angolo α, formato dalle due
semirette a e b con vertice O, si può ricorrere
alla seguente costruzione.
c
O
S
α
R
a
Con un compasso, facendo centro in O, si traccia
un arco c che interseca la semiretta a in R e la
b’
semiretta b in S. Dopodiché, tracciata la semiretta
a’ con origine in O’ dove si vuole trasportare l’angolo
c’ S’
α, facendo centro in O’, senza variare l’apertura del
s
compasso, si traccia l’arco c’ che interseca a’ in R’
α’
A questo punto, con centro in R’ e con l’apertura del
a’ ’
compasso uguale al segmento RS si traccia l’arco s
O’
R’
che interseca l’arco c’ nel punto S’.
Congiungendo O’ con S’ si ottiene la semiretta b’, che con la a’ forma l’angolo R’O’S’,
α ≅ α’
congruente a quello dato.
3.28
Confronto tra due angoli
Confrontare due angoli significa verificare se essi sono congruenti o se uno è maggiore
o minore dell’altro.
Per effettuare il confronto si deve trasportare il lato a’
b ≡ b’
dell’angolo α’ sul lato a dell’altro angolo, facendo in
modo che i due vertici O ed O’ coincidano e che b’
α ≅ α’
si trovi dalla stessa parte di b.
O ≡ O’
a ≡ a’
Si possono verificare tre casi:
b’
1°) il lato b’ si sovrappone esattamente sul lato b:
in questo caso i due angoli sono congruenti e si
α
b
scrive α ≅ α’.
α’
a ≡ a’
2°) il lato b’, cade al di fuori dell’angolo α: in tal O ≡ O’
caso α è minore di α’ e si scrive α < α’;
3°) il lato b’ cade all’interno dell’angolo α: in tal
b
21
caso α è maggiore di α’ e si scrive α > α’.
3.29
Somma di due o più angoli e sue proprietà
b’
α
Dati due o più angoli consecutivi, ROS ed SOT,
la loro somma è l’angolo ROT, formato dai lati non
comuni degli angoli dati e si scrive:
ROS + SOT = ROT
α’
O ≡ O’
a ≡ a’
T
Se gli angoli da sommare non sono consecutivi,
O
S
per farne la somma si costruiscono altrettanti
angoli consecutivi congruenti a quelli dati.
R
La loro somma è l’angolo avente per lati i lati non comuni.
Due angoli sono congruenti se sono la somma di angoli rispettivamente congruenti.
La somma di due o più angoli gode di tutte le proprietà della somma dei numeri naturali,
cioè: la proprietà commutativa e la proprietà associativa.
La somma di due angoli adiacenti è un angolo piatto
La somma di due angoli piatti è un angolo giro.
3,30
B
Multipli e sottomultipli di un angolo
Dato un angolo α = AOB, la somma di più angoli
congruenti ad α è un multiplo di α
Nella figura l’angolo RO’S è uguale a tre volte α
e si scrive
RO’S = 3 AOB
α
O
A
S
Se si confronta l’angolo AOB con l’angolo RO’S
si rileva che AOB è la terza parte di RO’S e si
scrive
AOB = 1/3 RO’S
In questo caso si dice che AOB è un sottomultiplo
di RO’S.
3.31
α
α
O’
α
Differenza di due angoli
R
S
La differenza tra due angoli disuguali, ad es.
ROS > ROT , è l’angolo che addizionato al
minore dà come somma.il maggiore e si
scrive
ROS - ROT = TOS
Ovviamente se i due angoli sono congruenti la
loro differenza è nulla.
3.32
T
O
R
Angoli supplementari
Due angoli la cui somma è un angolo piatto si dicono
supplementari. ( α + β = π )
Due angoli adiacenti sono supplementari, ma due
angoli possono essere supplementari senza essere
adiacenti.
3.33 Angolo retto
22
α
β
L’angolo retto è esattamente la metà dell’angolo piatto.(π/2)
Per costruirlo graficamente si può, mediante un compasso,
puntato prima su uno e poi sull’altro estremo del segmento
C
AB, che rappresenta un angolo piatto di cui il punto O è
il vertice, tracciare due archi di uguale raggio, maggiore di
Q
P
AO: ad es. AP = QB.
A
O
B
Questi due archi si intersecano nel punto C.
Congiungendo C con O si ottengono due angoli, AOC
e COB che sono retti. Anche AOD e DOB sono retti.
Ovviamente tutti gli angoli retti sono congruenti
D
La somma di due angoli retti è l’angolo piatto.
La somma di quattro angoli retti è l’angolo giro.
Per costruire graficamente un angolo retto si può anche fare uso di una squadra, di cui un
angolo è sempre un angolo retto.
B
3.34 Bisettrice di un angolo
N
Dato un angolo AOB, volendo dividerlo in due parti uguali,
C
si traccia un qualsiasi arco con centro in O, che interseca
O
i lati dell’angolo dato in M ed N.
Ora, con centro prima in M e poi in N e con la stessa
M
A
apertura del compasso, si tracciano due archi che si intersecano in C. La semiretta OC
divide l’angolo dato in due parti, ognuna uguale alla metà dell’ angolo dato.
La semiretta OC si chiama bisettrice dell’angolo.
3.35
Angoli acuti ed ottusi – Angoli complementari
angolo acuto
Gli angoli minori dell’angolo retto si dicono acuti; quelli
maggiori dell’angolo retto si dicono ottusi.
Due angoli acuti la cui somma è un angolo retto si dicono
complementari
Due angoli complementari di uno
stesso angolo sono tra loro congruenti-
angolo ottuso
a
3.36
RETTE PERPENDICOLARI
90°
90° 90°
90°
Due rette incidenti a e b, che, intersecandosi, dividono
il piano su cui giacciono in quattro angoli retti, sono tra
loro perpendicolari.
Due rette incidenti, ma non perpendicolari, si dicono
oblique.
Per un dato punto R passa una ed una sola retta
perpendicolare ad una retta data r
Il punto P in cui la perpendicolare per R interseca la
retta r si chiama piede della perpendicolare.
Il segmento RP che unisce i punti R e P, si chiama
distanza del punto dalla retta ed è il minore tra i segmenti
23
b
•R
r
P
che congiungono
3.37
R con un qualsiasi punto della retta.
a
Asse di un segmento
A
La perpendicolare a che passa per il punto medio M di
un segmento AB, si chiama asse del segmento.
Per costruirlo graficamente si deve operare nel modo
seguente:
Con un compasso, facendo centro prima in A e poi in B,
si tracciano due archi con raggio uguale, maggiore di AM.
Essi si intersecano in R ed in Q. La retta che passa per
R e per Q è l’asse cercato.
M
B
Q
A
B
R
L’asse di un segmento può essere definito come la
perpendicolare a tale segmento i cui punti hanno uguale distanza dagli estremi del
segmento stesso.
3.38
Perpendicolare da un punto ad una retta
Per costruire la perpendicolare da un punto P ad una retta r, si devono considerare due
casi
1° caso Il punto P sta sulla retta r
In questo caso, con un compasso, facendo
centro in P, si traccia una circonferenza di
raggio qualunque, che interseca la r nei due
punti A e B. Quindi, sempre con il compasso,
facendo centro prima in A e poi in B, con
raggio maggiore di AP, si descrivono due
archi che si intersecano in R ed in S.
La retta RS che passa per P è la
perpendicolare voluta.
S
r
A
P
B
R
•P
2° caso Il punto P è esterno alla retta r
In questo caso si fissano arbitrariamente sulla retta due
punti A e B in modo che i segmenti AP e BP siano
uguali. Dopodiché si opera come per la costruzione
dell’asse di un segmento (v. § precedente), ottenendo
la perpendicolare voluta.
3.39
r
•
•
A
B
RETTE PARALLELE
Due o più rette giacenti sullo stesso piano, ma senza
alcun punto in comune, si dicono parallele.
Molte rette parallele costituiscono un fascio improprio,
mentre è detto proprio il fascio formato dalle infinite rette che passano per un punto
24
( v. § 3.9 ).
3.40
Parallela per un punto ad una retta
Per costruire per un punto P una retta parallela ad una retta data r si può fare uso di
una riga e di una squadra, disposte come in figura.
r
s
La squadra va prima posta nella posizione 1, di modo
che il più lungo dei suoi lati AB coincida con la retta r
B
data. Poi si accosta la riga al lato piu corto AC che è
P•
perpendicolare ad AB. Si sposta quindi la squadra in
1
2
modo che ll lato AB passi per il punto P e senza più
muovere nè la riga, né la squadra, si traccia la retta
A squadra C
s che è la parallela alla r, voluta.
riga
r
Il postulato di Euclide afferma che: per un punto, non appartenente ad una retta, si può
condurre una ed una sola parallela ad essa.
3.41
Angoli formati da due rette parallele tagliate da una trasversale
Due rette parallele a e b tagliate da una terza retta t detta trasversale, che interseca a
e b, rispettivamente, in A e in B, formando quattro angoli con vertice in A e quattro
angoli con vertice in B.
Tali angoli, a due a due, hanno dei nomi particolari.
t
a
1A2
Gli angoli 3 e 6 ; 4 e 5 si chiamano alterni interni
.
3 4
e sono congruenti.
Gli angoli 1 e 8 ; 2 e 7 si chiamano alterni esterni
e sono congruenti.
b
5B 6
Gli angoli 1 e 5 ; 2 e 6 ; 3 e 7 , 4 e 8 si chiamano
7 8
corrispondenti e sono congruenti.
Gli angoli 3 e 5 ; 4 e 6 si chiamano coniugati interni e sono supplementari.
Gli angoli 1 e 7 ; 2 e 8 si chiamano coniugati esterni e sono supplementari.
.
Si può quindi riassumere. Due rette parallele tagliate da una trasversale formano con
essa. angoli alterni interni ed esterni congruenti, angoli corrispondenti congruenti
ed angoli coniugati interni ed esterni supplementari.,
3.42
Distanza tra due rette parallele
Date due rette parallele a e b, prendendo a caso
due punti A e B sulla retta a e conducendo per
essi le perpendicolari a tale retta, esse incontrano la
parallela b rispettivamente in C e D.
I segmenti AC e BD, che sono congruenti,
rappresentano la distanza tra le parallele.
La parte di piano compresa tra le due parallele
si chiama striscia.
3.43
b
a
C
D
A
B
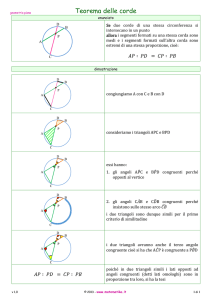
Rette parallele tagliate da due trasversali – Teorema di Talete
25
Date due o più rette parallele, equidistanti, tagliate da
due rette trasversali, si può facilmente constatare che
D
D’
i segmenti che le parallele staccano su ognuna delle
trasversali sono congruentii: AB ≅ BC ≅ CD e così
C
C’
pure A’B’ ≅ B’C’ ≅ C’D’
I segmenti sulle trasversali,. compresi tra due parallele,
B
B’
come AB e A’B’, si dicono corrispondenti od omologhi
Se si considera il segmento AD che è il triplo di AB, si
A
A’
constata che anche il segmento A’D’ è il triplo di A’B’.
Si può quindi affermare che il rapporto tra i segmenti
su una trasversale, compresi tra due parallele qualsiasi,
è uguale al rapporto tra i segmenti omologhi posti sull’altra trasversale.Si può concludere
con il teorema di Talete (detto: corrispondenza di Talete) che afferma:
Dato un fascio di rette parallele tagliate da due trasversali, il rapporto tra due
segmenti posti su una trasversale è uguale al rapporto tra i segmenti omologhi
dell’altra trasversale. E viceversa.
3.44
Divisione di un segmento in parti uguali
Volendo dividere un segmento AB in un certo numero di parti congruenti, ad es. 5, si
opera come segue .Con l’origine in A si conduce la semiretta s sulla quale, a partire da
A, si portano 5 segmenti qualsiasi congruenti: AC ≅ CD ≅ DE ≅ EF ≅ FG.
G
Quindi si unisce G con B e dagli estremi dei vari
F
segmenti posti sulla s si conducono le parallele al
E
segmento GB. Esse intersecano AB nei punti
D
C’, D’, E’, F’ Per il teorema di Talete (v. § 3.43)
C
i segmenti AC’, C’D’, D’E’, E’B sono congruenti.
A C’ D’ E’’ F’ B
3.45 POLIGONI
Si chiama poligono la parte di piano racchiusa da una spezzata ( v. § 3.18) chiusa, detta
poligonale semplice.
D
La poligonale ha il nome di contorno; i vertici ed i lati della
poligonale sono i vertici ed i lati del poligono.
C
La somma dei lati del poligono si chiama perimetro.
E
Il numero dei vertici di un poligono è uguale al numero dei lati.
Il poligono prende il nome dal numero dei lati (derivato dal greco)
Un poligono con 3 lati si chiama triangolo;
A
B
“
“
“ 4 “ “
“
quadrilatero o quadrangolo;
“
“
“ 5 “ “
“
pentagono;
“
“
“ 6 “ “
“
esagono;
“
“
“ 7 “ “
“
eptagono;
“
“
“ 8 “ “
“
ottagono;
“
“
“ 9 “ “
“
ennagono;
“
“
“ 10 “ “
“
decagono;
“
“
“ 12 “ “
“
dodecagono:
26
Non ricordando il nome specifico di un poligono lo si può indicare con il numero dei lati: ad
es. si può dire poligono di sette lati invece di eptagono.
D
E’ ovvio che ogni lato di un poligono è minore della somma
E
dei suoi lati (perimetro), ma è anche vero che ogni lato è
minore della somma di tutti gli altri.
C
Gli angoli del poligono formati da due lati consecutivi, come
AED, si chiamano angoli interni; invece quelli formati da un
A
lato e dal prolungamento di uno dei lati consecutivi, come
B
CBF, si chiamano angoli esterni, che sono supplementari
F
degli angoli interni, adiacenti. La somma degli angoli ABC
e CBF è un angolo piatto
Ogni segmento che unisce due vertici non consecutivi si chiama
diagonale
Da ogni vertice di un poligono di n lati escono tante diagonali.quanti sono i lati
meno 3 (ad es, da ogni vertice di un pentagono escono 2 diagonali)
Il numero delle diagonali distinte di un poligono di n lati è uguale alla metà del
prodotto del numero dei lati , per lo stesso numero ridotto di 3 (ad es.un pentagono
ha 5 • 2 / 2 = 5 diagonali distinte).
3.46
Poligoni concavi e convessi
Un poligono situato tutto da una parte
A
rispetto alle rette passanti per ognuno
dei suoi lati, come la figura A, si dice
poligono convesso.
Un poligono che è diviso in due parti
da almeno una retta passante per uno
dei suoi lati, come la figura B, i si dice poligono concavo.
3.47
B
TRIANGOLI E LORO PROPRIETÀ
Il più semplice tra tutti i poligoni è quello con tre soli lati chiamato triangolo.
I tre lati ed i tre angoli di un triangolo si chiamano elementi del
triangolo. I punti A, B e C ne sono i vertici.
Un lato e l’angolo il cui vertice non appartiene al lato si dicono
opposti.
α
Un lato ed un angolo il cui vertice appartiene al lato si dicono
adiacenti
A
C
γ
β
B
In qualsiasi triangolo ogni lato è minore della somma
degli altri due e maggiore della loro differenza.
A differenza di altri poligoni il triangolo è una figura chiusa indeformabile, per cui esso è
un elemento insostitubile nella scienza delle costruzioni..
3.48
Classificazione dei triangoli rispetto ai lati
27
Con riferimento ai lati, un triangolo si chiama:
scaleno, se non ha alcuna coppia di lati conguenti;
isoscele, se ha due lati congruenti;
equilatero, se ha i tre lati congruenti
3.49
Proprietà dei triangoli
Ecco alcune proprietà fondamentali dei triangoli.
γ
Un triangolo può avere al massimo un angolo retto.
β
Un triangolo può avere al massimo un angolo ottuso.
Un angolo esterno di un triangolo è uguale alla somma
dei due angoli interni non adiacenti ad esso. (nella figura α = β + γ )
α
Un angolo esterno di un triangolo è maggiore di ciascun angolo interno non
adiacente.
Se due angoli di un triangolo sono rispettivamente congruenti a due angoli di un
altro triangolo, anche i rimanenti angoli sono congruenti.
3.50
Somma degli angoli interni di un triangolo
Dato un qualsiasi triangolo ABC, per calcolare la somma dei suoi angoli interni si deve
condurre per uno dei suoi vertici la retta parallela p al lato opposto AB.
Considerando gli angoli si constata che l’angolo α è congruente ad α’ perché essi sono
angoli alterni interni delle due parallele p ed AB
C
,
tagliati dalla trasversale AC .
p
La stessa cosa vale per gli angoli β e β’. Poiché,
β’
α’
come si vede in figura, la somma α’ + β’ + γ è
γ
uguale ad un angolo piatto, anche la somma degli
angoli α +β + γ è uguale ad un angolo piatto.
α
β
Si può quindi concludere che: la somma degli
angoli di un qualsiasi triangolo è un angolo piatto. A
B
3.51
Somma degli angoli interni di un poligono convesso
Dato un poligono convesso, se da uno qualsiasi
dei suoi vertici si conducono le diagonali agli altri
verticl, si può notare che il poligono viene diviso
in tanti triangoli quanti sono i lati, meno due.
Essendo evidentemente la somma degli angoli
interni del poligono uguale alla somma degli angoli
dei triangoli in cui il poligono stesso è stato suddiviso
dalle diagonali ed essendo la somma degli angoli di
un triangolo uguale ad un angolo piatto, si può
concludere che la somma degli angoli interni di un
poligono convesso è uguale a tanti angoli piatti,
quanti sono i lati, meno due.
3.52
Somma degli angoli esterni di un poligono convesso
28
Dato un poligono convesso, la somma degli angoli
3
esterni (1+2+3+4) più quelli interni (a+b+c+d) è
4 d
c
uguale, come si vede nelle figure, a tanti angoli
tanti quanti sono i lati, meno due. Se da questa
a
b 2
somma si sottrae il totale degli angoli interni, che,
1
come si è visto nel precedente §, è uguale a
tanti angoli piatti quanti sono i lati, meno due,
risulta che la somma degli angoli esterni di un
poligono convesso è uguale al numero dei lati,
diminuito dello stesso numero dei lati meno due,
5 e
cioè due angoli piatti
Fig B
A differenza della somma degli angoli interni, che
dipende dal numero dei lati, la somma degli angoli
a
esterni di un poligono convesso è sempre uguale
1
a due angoli piatti, qualunque sia il numero dei suoi lati.
3.53
Fig A
4
d
3
c
b 2
Classificazione dei triangoli rispetto agli angoli
Con riterimento agli angoli, un triangolo si chiama:
acutangolo, se ha tutti e tre gli angoli acuti;
rettangolo, se ha un angolo retto (e quindi gli altri due acuti)
ottusangolo, se ha un angolo ottuso (e quindi gli altri due acuti)
3.54 Triangolo scaleno
Un triangolo con i tre lati ed i tre angoli non congruenti si chiama
scaleno.
3.55
Triangolo isoscele
Un triangolo con due lati congruenti si chiama isoscele.
I due lati congruenti si chiamano semplicemente lati Il terzo lato
è detto base. Gli angoli compresi tra la base ed uno dei lati si
chiamano angoli alla base e sono congruenti. Il terzo angolo si
chiama angolo al vertice.
V
Per costruire graficamente un triangolo isoscele, scelto un punto
come vertice V, mediante un compasso con l’apertura uguale al
lato del triangolo da costruire, facendo centro in V si traccia un
arco s. Prendendo su tale arco due punti la cui distanza sia
congruente alla base del triangolo da disegnare ed unendoli tra
loro e poi entrambi al vertice V si realizza la costruzione voluta.
s
A
B
3.56 Triangolo equilatero
Un triangolo con i tre lati congruenti si chiama equilatero.
Poiché in questo tipo di triangolo anche i tre angoli sono tra
loro congruenti, si può anche chiamare equiangolo.
29
C
Per costruirlo graficamente, avendo il lato AB, mediante un
compasso, con apertura uguale ad AB, facendo centro in A
e poi in B, si tracciano due archi che si intersecano in C
Congiungendo A e B con C si ottiene il triangolo voluto.
3.57
A
B
Triangolo rettangolo
Un triangolo con un angolo retto e due, ovviamente, acuti, si chiama rettangolo
Il lato opposto all’angolo retto si chiama ipotenusa; gli altri due lati hanno il nome
dii cateti.
Seguono alcune proprietà del triangolo rettangolo.
L’ipotenusa è maggiore di ciascun cateto
I due angoli acuti di un triangolo rettangolo sono tra loro complementari.
3.58
3.58.1
Elementi notevoli di un triangolo
C
Altezze – Ortocentro
In un qualsiasi triangolo il segmento di perpendicolare condotto
da un vertice C al lato opposto AB, si chiama altezza del
triangolo relativa al lato AB, che prende il nome di base.
O
A
Si può quindi affermare: l’altezza di un triangolo relativa
ad una base, è la distanza del vertice opposto, dalla
base stessa.
Se si tracciano le tre altezze di un triangolo si constata
che esse passano tutte per uno stesso punto O detto
ortocentro
Se il triangolo è ottusangolo l’ortocentro è all’esterno del
triangolo ed è il punto di intersezione delle altezze relative
ai prolungamenti di alcuni lati.
B
C
A
B
O
3.58.2 Bisettrici dei tre angoli di un triangolo - Incentro
C
In qualsiasi triangolo i segmenti che dividono gli angoli
In due parti congruenti l’una all’altra, si chiamano bisettrici
degli angoli del triangolo (v. § 3.34)
Se si tracciano le tre bisettrici di un triangolo si osserva che
esse passano tutte per lo stesso punto I detto incentro.
3.58.3
I
A
P
Assi dei tre lati di un triangolo - Circocentro
In un triangolo qualsiasi i segmenti perpendicolari ai lati nel
loro punto medio si chiamano assi dei tre lati di un triangolo.
Se si tracciano i tre assi di un triangolo si constata che
essi passano tutti per lo stesso punto C, detto circocentro.
30
C
B
3.58.4
Mediane dei tre lati di un triangolo- Baricentro
In un qualsiasi triangolo i segmenti che uniscono i vertici
con il punto medio dei lati opposti si chiamano mediane.
Le tre mediane si incontrano in uno stesso punto B
detto baricentro del triangolo.
B
Il baricentro divide ogni mediana in due parti, di cui quella
con un estremo nel vertice è doppia dell’altra..
3.59 ISOMETRIE NEL PIANO
Euclide sosteneva che due figure sono uguali quando ognuna può essere spostata con
un movimento rigido e portata a sovrapporsi esattamente sull’altra.
Questa definizione non è accettabile perché l’uguaglianza viene definita facendo ricorso
ad un movimento rigido e quest’ultimo è definito per mezzo dell’uguaglianza. Oltretutto
non si può essere certi che il suddetto movimento non provochi delle deformazioni nelle
figure spostate. Per giungere ai concetti di isometria e di congruenza si parte dalla
definizione di trasformazione geometrica nel piano, che è una corrispondenza
biunivoca tra i punti del piano stesso.
Si chiama trasformazione isometrica o isometria (dal greco: isos = uguale; metron =
misura) una trasformazione geometrica piana che conserva la distanza tra punti.
Una isometria che ad ogni punto associa se stesso si dice trasformazione identica o
identità.
Poiché una figura geometrica può essere considerata come un sottoinsieme di punti del
piano, una trasformazione geometrica associa ad una figura un’altra figura detta figura
trasformata.
Ad es. il segmento A’B’ è il trasformato del segmento AB
In una trasformazione geometrica si dicono:
invarianti le proprietà di una figura che nella trasformazione rimangono invariate;
uniti i sottoinsiemi di una figura che coincidono con la propria trasformata.
Se esiste una trasformazione geometrica che ad ogni punto di una figura associa ogni
punto di un’altra, le due figure si dicono equivalenti.
Mentre Euclide attribuiva significati differenti ai concetti di uguaglianza e di equivalenza,
dando al termine equivalenza il significato di uguale estensione ed al termine
uguaglianza il significato di uguale forma ed uguale estensione, la geometria moderna
dà praticamente ai due termini lo stesso significato, però, volendo affermare che due
figure sono equivalenti, occorre specificare rispetto a quale proprietà.
In questo testo il termine equivalenza sarà usato per indicare che due figure si
corrispondono in una trasformazione geometrica.
Si dice involutoria o a carattere involutorio l’isometria che, applicata due volte,
coincide con l’identità, cioè una trasformazione che fa tornare ogni punto su se stesso.
31
L’applicazione successiva di due o più trasformazioni geometriche si chiama
prodotto di trasformazioni o composizione di isometrie.
Il prodotto di due o più isometrie è ancora un’isometria.
Sono isometrie: le simmetrie, le traslazioni e le rotazioni. (Non lo sono, invece, le
omotetie e le similitudini,, che verranno trattate in seguito.)
3.60
Simmetria assiale
Data nel piano una retta r si chiama simmetria assiale di asse r , ed è indicata con Sr,
una trasformazione geometrica piana avente le seguenti proprietà:
1 ogni punto dell’asse r è un punto unito;
2 ogni punto di un semipiano di frontiera r corrisponde ad un punto che si trova
nel semipiano opposto rispetto ad r;
3 la trasformazione è un’isometria;
P•
4 la trasformazione è involutoria.
In una simmetria assiale di asse r ad un punto P posto
r
in un semipiano ad una certa distanza dalla r, corrisponde
il punto P’ che sta nel semipiano opposto ad uguale
P•
distanza dalla r.
Se anziché un solo punto si considera una figura,
C
Sr
C’
geometrica (ad es. una figura come si vede nel
disegno a fianco), nella simmetria assiale di asse
r, al punto A corrisponde A’, a B corrisponde
A
A’
B’ ed infine a C corrisponde C’.
B
B’
3.61
Traslazione
Osservando il disegno a fianco si nota che la figura A’B’C’D’ è la trasformata di ABCD
nella simmetria assiale Sr e che la figura
A’’B’’C’’D’’ è la trasformata di A’B’C’D’
nella simmetria assiale Ss. con l’asse
C
C’
C’’
parallelo ad Sr..
D
D’ D’’
Si può quindi concludere che il prodotto
o composizione di due simmetrie assiali
B
B’
B’’
con gli assi paralleli, pur essendo una
A
A’
A’’’
isometria non è più una simmetria assiale
ma la isometria che si chiama traslazione.
Sr
Ss
Pertanto si può affermare che il prodotto di due simmetrie assiali ad assi paralleli
si chiama traslazione.
La traslazione gode delle seguenti proprietà;
1 la distanza tra due punti corrispondenti è costante;
2 le rette che congiungono due punti corrispondenti hanno la stessa direzione
( cioè stanno sulla stessa retta)
3 le rette che congiungono due punti corrispondenti hanno lo stesso verso
L’insieme di una distanza PQ = a, di una direzione e
di un verso prendono il nome di vettore, di cui a è il
32
Q
P
a
modulo, indicato con |a|
Una traslazione è individuata da uno ed un solo vettore.
Per indicare una traslazione di vettore AA’ si può usare il simbolo TAA’.
La traslazione inversa viene indicata con il simbolo TA’A:
Il prodotto di due traslazioni di vettore: TAA’ e TA’A’’, equivale alla traslazione TAA’’
3.62
Rotazione
D
C
C’
D’
Si è visto nel § precedente che la traslazione
è una isometria che consegue al prodotto
di due simmetrie assiali ad assi paralleli.
Se i due assi non sono paralleli ma incidenti, A
B
B’
A’ A’’
applicando ad una figura ABCD la simmetria
α
assiale Sr si ottiene la trasformata A’B’C’D’
Applicando poi la simmetria assiale Ss con
Ss O
l’asse incidente con quello precedentemente
B’’
D’’
considerato, si ottiene la figura A’’B’’C’’D’’ che
Sr
’
non è più la conseguenza di una traslazione
C’’
ma di un nuovo tipo di isometria detto rotazione.
Si può quindi affermare che la rotazione è il prodotto di due simmetrie assiali ad assì
incidenti.
Il punto O in cui si intersecano i due assi suddetti è detto centro di rotazione; infatti i
punti corrispondenti nelle due isometrie distano ugualmente da O.
L’angolo α è detto angolo di rotazione
La rotazione di un angolo nullo corrisponde all’identità.
Il prodotto di due successive rotazioni è ancora una rotazione.
Anche nelle rotazioni si può fare uso dei vettori: ad es. il vettore OB viene trasformato
prima nel vettore OB’ e poi nel vettore OB’’ che hanno tutti lo stesso modulo ma
dlfferenti direzioni.
3.63
Simmetria centrale
Se gli assi incidenti, di cui al precedente §, sono tra loro perpendicolari, si ottiene una
rotazione uguale ad un angolo piatto ( v. § 3.24 ).
Questa trasformazione isometrica del piano
si chiama simmetria centrale.
Si può affermare che la simmetria centrale
è il prodotto di due simmetrie assiali ad
A
C
C’
assi perpendicolari.
’
A’
Il centro di rotazione P di angolo uguale
B
B’
all’angolo piatto si chiama polo.
π
Ss
Nella simmetria centrale i punti corrispondenti,
P
come B e B’’, sono situati sulla stessa retta
BB’’, che passa anche per P.
’
B’’
C’’
A’’
La simmetria centrale è una isometria a carattere
Sr
Involutorio, cioè se si applicano due simmetrie
centrali con lo stesso polo si ottiene un’identità.
33
Se invece di un unico polo ce ne sono due,
distinti, il prodotto delle due simmetrie
centrali, una rispetto al polo P e l’altra
rispetto al polo P’,equivalgono ad una
traslazione.
C
C’’
’
A
B
Si può quindi affermare che il prodotto.
di due simmetrie centrali, rispetto a
poli diversi, equivale ad una traslazione
P
π
A’’’
P’
B’’
Ss
B’
π
’
A’
Sr
3.64
CONGRUENZE
C’
St
Era già stato fatto un cenno sulla congruenza nel § 3.8
Le infinite coppie ordinate di punti del piano, come (P,P’), generano una corrispondenza
biunivoca tra i punti del piano, che si chiama congruenza.
Per indicare che due figure geometriche F ed F’ si corrispondono in questa
corrispondenza biunivoca si dice che sono congruenti: si scrive F ≅ F’ e si legge
F è congruente ad F’
Si può anche dire che due figure geometriche si dicono congruenti quando si
possono trasformare l’una nell’altra mediante una congruenza.
La relazione generata tra i punti del piano dalla congruenza si chiama relazione di
congruenza.
Due figure congruenti godono delle seguenti proprietà:
riflessiva
F≅ F;
simmetrica: F ≅ F’ ⇒ F’ ≅ F;
transitiva (F≅ F’) e (F’≅ F’’) ⇒ ( F ≅ F’)
3,65
I criteri di congruenza dei triangoli
Nel precedente § si è detto che due figure geometriche sono congruenti se esiste un
movimento rigido, cioè senza deformazione, che permetta di sovrapporle perfettamente
l’una sull’altra. Talvolta però non è possibile realizzare la sovrapposizione con un
movimento rigido, però se si sa che le due figure hanno i lati ordinatamente congruenti,
questo basta per concludere che due figure sono
sovrapponibili e quindi congruenti.
Tuttavia, se in due triangoli le tre coppie di angoli
γ
Sono ordinatamente congruenti, ciò non è sufficiente
γ
per concludere che i due triangoli sono congruenti.
Infatti pur essendo congruenti i tre angoli, i lati dei
α
β
α
β
due triangoli possono essere diversi (v. figura) e
quindi i due triangoli non sono congruenti.
I criteri di congruenza di due triangoli sono tre.
Si suppone che le due figure da confrontare siano sullo stesso piano e che siano
ugualmente orientate.
Nel caso che non lo fossero possono essere rese tali mediante un movimento rigido, come
ad es. una rotazione.
34
3.66 Primo criterio di congruenza dei triangoli
Il primo criterio di congruenza dei triangoli afferma: Due triangoli sono congruenti se
hanno due lati e l’angolo tra essi compreso ordinatamente congruenti.
Ipotesi: AC ≅ A’C’ ; BC ≅ B’C’ ; γ ≅ γ’
C
C’
Tesi: ABC ≅ A’B’C’
Dimostrazione:
^γ
^γ’
Una congruenza che associ all’angolo
x
x
x
x
γ il suo congruente γ’, in modo che
x
x
le semirette CA e CB siano
corrispondenti delle semìrette C’A’
A
B A’
B’
e C’B’, associa ai segmenti CA e
CB i segmenti omologhi C’A’ e C’B’.
Quindi questa congruenza associa ai tre vertici del primo triangolo i tre vertici
corrispondenti del secondo, per cui si può concludere che i due triangoli sono
congruenti.
C.v,d.
3.67
Secondo criterio di congruenza dei triangoli
Il secondo criterio di congrenza dei triangoli
afferma: Due triangoli sono congruenti se
C
C’
hanno un lato e due angoli ordinatamente
congruenti.
Ipotesi: AB ≅ A’B’ ; α ≅ α’ ; β ≅ β’
Tesi: ABC ≅ A’B’C’
α
||
β
α’ ||
β’
Dimostrazione:
A
B
A’
B’
Una congruenza che associ all’angolo α i’angolo α’ in modo che alle semirette AB
e AC corrispondano ordinatamente le semirette A’B’ e A’C’, associa al segmento AB
il segmento A’B’ ed all’angolo β l’angolo congruente β’. Quindi anche al vertice C, che
è l’intersezione dei segmenti AC e BC, corrisponderà il punto C’, che è l’intersezione
dei corrispondenti segmenti A’C’ e B’C’.
Poiché questa corrispondenza associa ai tre vertici del primo triangolo i tre vertici
corrispondenti del secondo, si conclude che i due triangoli sono congruenti. C.v.d.
3.68
Terzo criterio di congruenza dei triangoli
Secondo il terzo criterio di congruenza dei triangoli: Due triangoli sono congruenti se
hanno i lati ordinatamente congruenti.
C
C’
Ipotesi: AB ≅ A’B’ ; BC ≅ B’C’ ; CA ≅ C’A’
Tesi: ABC ≅ A’B’C’
Dimostrazione:
Sul semipiano opposto a quello in cui giace A
B A’
M
B’ r
il triangolo A’C’B’ viene riportato il triangolo
A’’C’’B’’. congruente con il triangolo ACB,
in modo che il lato A’’B’’ si sovrapponga
C’’
al lato A’B’.
Essendo congruenti i triangoli ACB e A’C’’B’ si ha AC ≅ A’C’’ e BC ≅ B’C’’
Quindi per le proprietà simmetrica e transitiva della congruenza (v. § 3.64) si ha pure
35
A’C’ ≅ A’C’’ e B’C’ ≅ B’C’’ per cui i due triangoli C’A’C’’ e C’B’C’’ sono isosceli ed
hanno quindi gli angoli alle rispettive basi congruenti: A’C’C’’≅ A’C’’C’ e B’C’C’’≅ B’C’’C’.
Poiché i punti C’ e C’’ si trovano nei due semipiani opposti rispetto alla retta r su cui
giace il segmento A’C’, il segmento C’C’’ che li unisce, interseca la retta r ( v. § 3.21)
in un punto indicato con M.
Se, come è in figura, il punto M sta fra A’ e B’ i due angoli A’C’B’ e A’C’’B’ risultano
congruenti perché somme di angoli rispettivamente congruenti (v. § 3.29).
Pertanto i due triangoli A’B’C’ e A’B’C’’, avendo due lati e l’angolo compreso congruenti,
per il primo criterio di congruenza sono congruenti e di conseguenza, per la proprietà
transitiva, sono congruenti i due triangoli dati.
C.v.d.
Nel caso che il punto M cada fuori del lato A’B’, il ragionamento precedente è ancora
valido, però, anziché di somme si deve parlare di differenze di angoli congruenti.
3.69 Criteri di congruenza dei triangoli rettangoli
Per i triangoli rettangoli valgono i seguenti criteri di congruenza: Due triangoli rettangoli
ABC e A’B’C’, con l’angolo retto rispettivamente in A ed A', sono congruenti se
hanno congruenti:
C1
i cateti; (V. il primo criterio)
un cateto ed un angolo acuto; (V. ii secondo criterio)
l’ipotenusa ed un angolo acuto; ( V. il terzo criterio)
B1
l’ipotenusa ed un cateto. ( V. la dimostrazione qui sotto )
r A1
Ipotesi: AB ≅ A’B’ ; BC ≅ B’C’
A’1
B’1
Tesi: ABC ≅ AB’C’
Dimostrazione
Se si considerano i due triangoli A1B1C1 e A’1B’1C’1,
C’1
( rispettivamente congruenti ai triangoli dati ), posti in modo C
C’
che abbiano in comune i cateti congruenti A’1B’1 e A1B1
ed i vertici C’1 e C1, situati nei semipiani opposti rispetto
alla retta r su cui giacciono i cateti A’1B’1 e A1B1,,,si
vede che tali triangoli, simmetrici rispetto alla r, sono
congruenti e pertanto anche i triangoli dati sono
A
B A’
B’
congrenti.
C.v.d.
3.70
QUADRILATERI
Nel § 3.45 era stato detto che i poligoni con quattro lati si chiamano quadrilateri o
quadrangoli.
Dopo i triangoli essi sono i poligoni più semplici.
Nei quadrilateri:
- due lati sono consecutivi se hanno un estremo in comune; in caso contrario
sono opposti;
- due vertici sono consecutivi se sono gli estremi di uno stesso lato; in caso contrario
sono opposti;
- due angoli sono consecutivi se lo sono i rispettivi vertici; in caso contrario
sono opposti se lo sono i rispettivi vertici.
36
3.71
Trapezi
Si chiama trapezio ogni quadrilatero convesso avente una coppia di lati opposti
paralleli.
Base minore
I due lati paralleli si chiamano basi, di cui la più lunga
è detta base maggiore e l’altra base minore
Altezza
Lato obliquo
I rimanenti lati si chiamano lati obliqui (o lati).
La distanza tra le due basi si chiama altezza.
Base maggiore
Poiché il trapezio ha due lati paralleli valgono le seguenti
relazioni tra i suoi angoli: ( V. § 3.41)
Gli angoli adiacenti ad uno stesso lato obliquo
β
sono supplementari. (α + β = π )
Gli angoli compresi tra le basi ed una diagonale
α
sono congruenti. (α ≅ α’)
α’
α
π/2
Un trapezio si dice rettangolo se ha un lato perpendicolare
alla base. (v. figura)
π/2
Un trapezio si dice isoscele se ha i lati obliqui tra loro
congruenti e paralleli.
In un trapezio isoscele:
Gli angoli adiacenti ad entrambe le basi sono congruenti;(α ≡ α’) α
Le diagonali sono tra loro congruenti.
3.72
α’
Parallelogrammi
Il parallelogramma è un particolare trapezio che ha due coppie
di lati paralleli invece di una sola.
Per cui si chiama parallelogrammo ogni quadrilatero che
ha i lati opposti tra loro paralleli.
Uno qualunque dei lati può essere considerato come base.
L’altezza relativa a quella base è la distanza tra la base ed
il lato opposto.
Altezza
Base
x
Poiché il parallelogrammo ha i lati opposti paralleli valgono
le seguenti relazioni:
:
Angoli adiacenti ad uno stesso lato sono supplementari
(come per il trapezio):
Ciascuna diagonale divide il parallelogrammo in due
triangoli congruenti per cui i lati opposti sono
congruenti e gli angoli opposti sono congruenti;
In ogni parallelogrammo:
Le diagonali lo dividono in quattro triangoli a due a due
congruenti
Le diagonali si dividono a metà e quindi hanno lo stesso
punto medio M che si chiama centro del parallelogrammo.
E viceversa.
37
||
||
x
M
3.73
Parallelogrammi particolari
Tra i parallelogrammi ce ne sono tre con particolari caratteristiche.
Essi sono: il rettangolo, il rombo ed il quadrato.
3.74
Rettangolo
Si chiama rettangolo ogni parallelogrammo con tutti gli angoli retti.
Ogni rettangolo ha:
Le diagonali congruenti
Il centro equidistante dai vertici;
Gli assi di ogni coppia di lati opposti coincidenti.
E viceversa
3.75
Rombo
Si chiama rombo ogni parallelogrammo con i quattro
lati congruenti.
Ogni rombo:
E’ diviso da entrambe le diagonali in due triangoli
Isosceli congruenti;
E’ diviso dalle due diagonali in quattro triangoli
rettangoli tutti congruenti tra loro;
Ha le diagonali perpendicolari:
Ha le diagonali coincidenti con le bisettrici dei relativi
angoli.
E viceversa.
3,76
Quadrato
Si chiama quadrato ogni parallelogrammo con quattro angoli retti e quattro lati
congruenti
Per i quadrati valgono tutte le proprietà enunciate per i rettangoli
e per i rombi.
3.77
Criteri di congruenza dei poligoni
I criteri di congruenza dei triangoli vengono estesi ai poligoni con un numero di lati
superiore a tre.
Condizione sufficiente affinché due poligoni, con lo stesso numero di lati, siano
congruenti è che siano rispettivamente congruenti tutti i lati e tutti gli angoli, ad
eccezione di:
un lato e due angoli adiacenti;
due lati consecutivi e l’angolo compreso fra essi;
tre angoli i cui vertici siano consecutivi.
38
Il termine “eccezione” non significa che i suddetti elementi non siano congruenti ma che,
semplicemente, non è necessario verificare la loro congruenza, perché è una
conseguenza delle altre.
3.78
Formula di Eulero per i poligoni
Se da un qualsiasi vertice di un poligono con n lati si conducono tutte le possibili
diagonali, il poligono risulta diviso in n-3 triangol,i che vengono definiti facce (f).
Se si dà il nome di spigoli (s), sia ai lati del poligono, sia alle diagonali, il numero
totale degli spigoli risulta uguale al numero dei lati più il numero delle diagonali.
Poligono
Numero
dei lati
Numero delle
diagonali
per vertice
n
Quadrilatero
Pentagono
Esagono
Ettagono
Ottagono
4
5
6
7
8
Numero
delle
facce
f
Numero
dei
vertici
v
2
3
4
5
6
4
5
6
7
8
1
2
3
4
5
Numero
degli
spigoli
s
5
7
9
11
13
Eulero trovò una relazione che lega i numeri f delle facce, ossia il numero dei triangoli in
cui il poligono viene diviso dalle suddette diagonali, il numero s degli spigoli ed il numero
dei vertici v del poligono.
Tale relazione è data dalla formula seguente: f + v – s = 1
E’ questa un invariante per i poligoni convessi, come lo è la somma degli angoli esterni,
sempre dei poligoni convessi, che è sempre uguale a 2π. (V. § 3.52)
3.79
I luoghi geometrici
Si chiama luogo geometrico l’insieme di tutti, e soli, gli oggetti che godono di una
medesima proprietà.
Una certa figura F è un luogo geometrico che soddisfa una certa proprietà p se:
Tutti i punti di F godono della proprietà p;
Non vi sono altri punti, al di fuori di F che hanno la p.
Ad es. l’asse di un segmento è il luogo geometrico dei punti del piano equidistanti dagli
estremi del segmento.
La bisettrice di un angolo è il luogo geometrico dei punti equidistanti dai lati dell’angolo.
3.80
CIRCONFERENZA E CERCHIO
Linea aperta
Una linea tale che nessuna delle sue parti sia un
segmento si dice curva, che può essere aperta o
chiusa.
Fra tutte le linee chiuse la più importante è la
circonferenza. (V. anche il § 3.22)
39
Linea chiusa
Linea chiusa
intrecciata
Si chiama circonferenza il luogo dei punti del piano equidistanti da un punto fisso O
detto centro .
La distanza costante tra i punti della circonferenza ed il centro si chiama raggio.
Ogni segmento che unisce due punti della circonferenza si chiama corda.
Le infinite corde che passano per il centro si chiamano diametri
Due circonferenze sono congruenti se sono congruenti i loro raggi.
La circonferenza racchiude una porzione di piano che si chiama cerchio.
Per inividure una circonferenza è sufficiente fissare un punto, che ne sia il centro ed un
segmento che ne sia il raggio. Si possono però fissare due punti di cui uno sia il centro e
l’altro un punto della circonferenza che, unito al centro, determina il raggio.
B
Per tre punti dati, A, B, C, non allineati, è possibile costruire
una circonferenza.
Si uniscono A con B e B con C; si tracciano gli assi dei
A
O
C
segmenti AB e BC che si intersecano nel punto O che,
essendo equidistante da A, da B e da C è il centro O della
circonferenza passante per i tre punti dati.
Ne consegue che due circonferenze distinte non possono avere più di due punti di
intersezione, perché altrimenti sarebbero un’unica circonferenza.
Una circonferenza non può aver punti allineati
B
M
Come già era stato accennato nel § 3.22 due punti A e B
su una circonferenza la dividono in due parti dette archi che
A
O
si distinguono l’uno dall’altro mediante una lettera, (ad es. M,
N ) posta vicino all’arco da individuare.
N
Si dice che la corda AB sottende l’arco AMB o l’arco BNA.
Se la corda AB è un diametro, i due archi, tra loro congruenti, si dicono
semicirconfrenze e le parti di cerchio corispondenti si chiamano semicerchi
A
3.81 Angolo al centro
α
Due raggi di una circonferenza OA ed OB dividono il
O
B
β
cerchio in due parti dette angoli al centro. ( α e β ),
Ad ogni arco e ad ogni corda corrisponde un angolo al
centro.
P
3.82 Angolo alla circonferenza
C
β
Se su una circonferenza di centro O e con un angolo al
β O
centro ( α ), delimitato dai raggi OA e OB, si sceglie un
α
B
punto P , l’angolo formato dalle corde AP e BP si
D
chiama angolo alla circonferenza ( β )
A .
40
Gli angoli alla circonferenza che sottendono uno stesso arco sono infiniti,e tutti congruenti
tra loro, come si vede in figura. Se fra essi si considera quello formato dal diametro BC
e dalla corda AC possiamo constatare che l’angolo al centro AOB, essendo un angolo
esterno rispetto al triangolo Isoscele COA, è uguale alla somma degli angoli ACB e
CAO ( V. § 3.47), che sono congruenti e pertanto risulta che l’angolo alla circonferenza
è la metà dell’angolo al centro che sottende la medesima corda.
Se si considera invece l’angolo APB, il diametro PD è la bisettrice sia di tale angolo sia
del corrispondente angolo al centro. Essendo isosceli i due triangoli APD e BPD, la metà
di α è uguale alla somma dei due angoli, congruenti, OPA e OAP, dei suddetti triangoli
isosceli e quindi anche in questo caso l’angolo al centro risulta il doppio dell’angolo alla
circonferenza.
Un angolo alla circonferenza che sottende un arco uguale
ad una semicirconferenza, la cui corda ovviamente è un
diametro, essendo l’angolo al centro un angolo piatto = π,
ne è la metà, cioè è π/2,
P
π/2
O
π
A
B
Si può quindi affermare che tutti i triangoli inscritti in una
semicirconferenza sono rettangoli.
Osservando la figura si può anche notare che in un triangolo rettangolo la mediana OP
relativa all’ipotenusa è la metà di questa: infatti la mediana è un raggio e l’ipotenusa
un diametro,
3.83
Proprietà delle corde
Le corde di una circonferenza godono delle seguenti proprietà:
Se due corde sono congruenti, gli archi e gli angoli al centro ad essi corrispondenti
sono congruenti;
Se dal centro di una circonferenza si conduce la perpedicolare ad una corda, questa
retta è l’asse della corda, dimezza i due archi da essa sottesi ed è la bisettrice di
ciascuno dei due angoli al centro che insistono su tali archi;
Corde congruenti hanno la stessa distanza dal centro; se non sono congruenti la
maggiore è la più vicina al centro.
3.84
Elementi del cerchio
A
In un cerchio ogni corda lo divide in due
parti dette segmenti circolari ad una base.
(nelle figure A e B)
A
B
C
B
Due corde parallele delimitano un segmento
circolare a due basi (in figura C).
Le parti di cerchio comprese tra due raggi si
chiamano settori circolari. ( in figura D
ed E )
41
D
E
3.85 Posizioni reciproche tra rette e circonferenze
Una retta, rispetto ad una circonferena giacente nello stesso piano, può assumere tre
differenti posizioni:
a
a) essere secante, cioè intersecare la circonferenza in due
punti. In questo caso la distanza della secante dal centro della
circonferenza O è minore del raggio della stessa.
O
b) essere tangente, cioè toccare la circonferenza in un punto,
,
detto punto di tangenza.T In questo caso la distanza della
r
tangente dal centro della circonferenza è uguale al raggio che,
b
nel suddetto punto, è perpendicolare alla tangente.
T
c) essere esterna, cioè non avere nessun punto di contatto
c
con la circonferenza. In questo caso la distanza della retta dal centro della circonferenza
è maggiore del raggio.
3.86
Proprietà della tangente ad una circonferenza
A
Se da un punto P esterno ad una circonferenza si conducono
le due tangenti alla stessa, i segmenti di tangente, compresi
tra P ed i punti di tangenza A e B, sono congruenti e la
semiretta s con origine in P, che passa per O , è la
P
bisettrice dell’angolo formato dalle tangenti.
s
O
B
Infatti: i triangoli AOP e BOP sono rettangoli e sono congruenti
perché hanno l’ipotenusa in comune e due cateti congruenti perché raggi della
circonferenza.
Essendo congruenti i triangoli lo sono anche gli angoli APO e BPO e quindi la s è
effettivamente la bisettrice dell’angolo APB.
C.v.d.
3.87
Posizioni reciproche di due circonferenze
Due circonferenze distinte possono assumere quattro diverse posizioni reciproche:
a) essere esterne l’una all’altra, cioè non avere alcun punto di contatto. Indicando con
d la distanza fra i centri, C e C’, delle due circonferenze, e con r ed r’ i rispettivi
raggi, è d > r + r’.
b) essere tangenti esternamente, cioè avere un unico punto di contatto R in cui le due
circonferenze si toccano. Le due circonferenze sono entrambe tangenti, una da una
parte, l’altra dall’altra, alla tangente t che passa per R ed è perpendicolare alla retta
dei centri. In questo caso, lo si vede immediatamente, è d = r + r’
In questa configurazione le due circonferenze hanno altre due tangenti comuni: p e q.
c) essere secanti, cioè intersecarsi reciprocamente in due punti, A e B. Se si
uniscono i centri delle circonferenze con uno di tali punti, ad es. A, per cui CA = r e
C’A = r’, ricordando che in un triangolo un lato è sempre minore della somma degli altri
due e maggiore della loro differenza, risulta d < r + r’ e d > r - r’.
d) essere tangenti internamente, cioè avere, anche in questo caso un unico punto di
contatto, ma le due circonferenze sono situate dalla stessa parte rispetto alla tangente
comune t. In questo caso è d ≅ r – r’.
e) essere una interna all’altra. In questo caso è d ≅ r – r’.
f) essere concentriche, cioè essere una interna all’altra ma con i centri coincidenti.
42
La porzione di piano compresa tra le due circonferenze si chiama corona circolare.
p
t
r’ C’
C
A
r
C
R
r
C
r’ C’
C’
B
q
a
b
a
C C’
r r’
d
3.88
c
C
r r C’
e
C≡C’
r’
r
f
Poligoni inscritti in una circonferenza
Un poligono si dice inscritto in una circonferenza se tutti i
suoi vertici sono sulla circonferenza.
A sua volta la circonferenza viene detta circoscritta al
poligono considerato.
Poiché è già stato detto che per tre punti non allineati passa un’unica circonferenza, se un
poligono è inscritto in una circonferenza questa è unica.
Non sempre per un poligono esiste la circonferenza circoscritta, se però ciò si verifica si
dice che il poligono è inscrittibile (o inscrivibile).
Ricordando quanto è stato detto nel § 3.58.3 a proposito del
punto di incontro dei tre assi di un triangolo, si può affermare
che ogni triangolo è inscrittibile in una circonferenza il cui
centro è il circocentro ( punto di incontro degli assi) del
triangolo stesso.
I quadrilateri sono inscrittibili in una circonferenza se, e solo
se, gli angoli opposti sono supplementari; lo sono quindi i
rettangoli, i quadrati ed i trapezi isosceli.
Si può anche affermare che un poligono è inscrittibile in una
circonferenza se gli assi dei suoi lati si incontrano tutti nello
stesso punto.
3.89
Poligoni circoscritti ad una circonferenza
Un poligono viene detto circoscritto ad una circonferenza
se tutti i suoi lati sono tangenti alla circonferenza stessa.
43
A sua volta la circonferenza è detta inscritta nel poligono considerato.
Se un poligono è circoscritto ad una circonferenza questa è unica.
Ogni poligono per il quale esiste la circonferenza inscritta viene detto circoscrittibile (o
circoscrivibile).
Tutti i triangoli sono circoscrittibili ed il centro della circonferenza inscritta è
l’incentro (punto di incontro delle bisettrici) del triangolo stesso ( v. § 3.58.2).
Non tutti i poligoni con più di tre lati sono circoscrittibii.
I quadrilateri sono circoscrittibii se, e solo se, la somma dei lati opposti è
congruente alla somma degli altri due lati, come ad es. nei rombi e quindi nei
quadrati.
Si può anche dire che un poligono è circoscrittibile se le bisettrici dei suoi angoli si
incontrano tutte nello stesso punto.
3.90 Poligoni regolari
Un poligono con tuttii lati congruenti tra loro è detto equilatero. Se sono congruenti tutti gli
angoli viene detto equiangolo
G
Un poligono equilatero ed equiangolo è un poligono regolare.
C
D
Ad es. il triangolo equilatero ed il quadrato sono poligoni regolari.
r
In generale si può affermare che un poligono equilatero inscritto H
O
F
in una circonferenza ed il poligono ad esso circoscritto, con i lati
tangenti alla circonferenza nei vertici del primo, sono regolari..
A
B
Infatti, sia dato il poligono equilatero (per esempio un quadrato)
ABCD, inscritto nella circonferenza di centro O e raggio r.
E
I lati del poligono, per ipotesi, sono tra loro congruenti e quindi lo sono anche gli archi da
essi sottesi. Se per i vertici del poligono si conducono le tangenti alla circonferenza, esse
si incontrano nei punti E, F, G, H, formando un poligono, EFGH, i cui lati fanno parte
delle suddette tangenti. Per dimostrare che il poligono dato, che è equilatero, è regolare.
bisogna dimostrare che è anche equiangolo.,
Gli angoli di tale poligono con i vertici in A e B. sono congruenti perché inscritti in archi
congruenti. Per lo stesso motivo sono congruenti due angoli qualunque del poligono,
quindi tale poligono è anche equiangolo, è quindi regolare.
Ogni poligono regollare è inscrittibile e circoscrittibile rispetto a due circonferenze
concentriche. Il centro il raggio della circonferenza circoscritta e di quella inscritta si
chiamano, rispettivamente, centro, raggio e apotema del poligono.
Il lato di un esagono regolare è congruente al raggio della circonferenza.
Se si divide una circonferenza in n archi congruenti:
il poligono convesso avente per vertici gli estremi degli archi è regolare;
il poligono convesso avente i lati tangenti negli estremi degli archi è regolare.
3.91
EQUIVALENZA DELLE SUPERFICI PIANE
Questo § tratta della misura dei poligoni; non però dei singoli lati o del loro perimetro, ma
della loro estensione (concetto assunto come primitivo).
44
Un poligono, un cerchio, un settore circolare, e così via, occupano una certa parte del
piano sul quale giacciono, che si chiama superficie piana della figura geometrica
considerata.
Due superfici piane qualunque, esattamente sovrapponibili e perciò congruenti, ad es. due
cerchi di uguale raggio, hanno la medesima superficie, cioè uguale estensione del
piano.
Però due superfici, pur avendo uguale estensione,
possono avere forme diverse. (V. figure )
3.92 Poligoni equivalenti
Due figure piane con la stessa estensione si dicono equivalenti ( o equiestese).
L’equivalenza viene indicata con il simbolo ≐
L’equivalenza tra due superfici piane è una relazione di equivalenza: infatti essa gode
delle tre solite proprietà: riflessiva, simmetrica e transitiva.
Se il poligono A ha una estensione maggiore di quella di B si dice che A è prevalente a
B o che B è suvvalente ad A.
3.93
Somme e differenze di superfici
Viene detta somma di due superfici piane A e B, senza parti in comune, eccetto
soltanto dei punti dei loro contorni, la superfice C formata dai punti di A e di quelli di B,
e si scrive C = A + B.
E’ detta differenza tra due superfici piane C e B la superficie A tale che C = A + B.
Somme e differenze di superfici piane equivalenti, sono equivalenti.
3.94
Poligoni equiscomponibili
Due poligoni si dicono equiscomponibili o equicomposti se si possono scomporre in
uno stesso numero di poligoni convessi, non aventi punti interni in comune e a due a due
congruenti tra loro.
Poligoni equiscomponibili sono equivalenti.
Due poligoni congruenti sono equiscomponibili ma non è vero il viceversa. Quindi per due
poligoni il fatto di essere equiscomponibil
è condizione necessaria ma non
sufficiente per essere congruenti.
Ad es. i due poligoni della figura
sono equiscomponibili ma non sono
congruenti.
3.95
Casi particolari di equivalenza di poligoni
Vengono dimostrati alcuni teoremi relativi a particolari poligoni equivalenti
1° CASO
Due parallelogrammi con le basi e le altezze rispettivamente congruenti, sono
equivalenti.
45
Per la dimostrazione D
L
C
H
G
conviene disegnare
due parallelogrammi
PQRS e PQZT,
rispettivamente
congruenti a quelli dati
A
B E M
F
con la base PQ in comune
e tale che i puntl R,S,T,Z,
S
T
R
Z
stiano sullo stesso semipiano rispetto
alla retta PQ.
Essendo per ipotesi le altezze congruenti
i lati opposti alle basi sono sulla stessa retta.
Si devono considerare tre alternative.
P
Q
a) I lati SR e TZ hanno in comune il segmento RT e quindi il trapezio PQRT.
I triangoli SPT e RQZ sono congruenti per il 1° criterio di congr uenza, perché
.
SP ≅ RQ, essendo lati opposti di un parallelogrammo;
.
SPT ≅ RQZ, essendo angoli con i lati paralleli e concordi. I parallelogrammi PQRS
e PQZT sono quindi equiscomponibili e, perciò equivalenti.
C.v.d.
b) Se T coincide con R i lati SR e TZ hanno un solo punto in comune.
La dimostrazione è simile a quella del caso precedente. I due parallelogrammi
hanno in comune il triangolo PQR ed i triangoli SPT e RQZ sono congruenti per il
primo criterio. La conclusione è quindi uguale a quella del 1° caso.
C.v.d.
c) I lati SR e TZ non hanno alcun punto in comune ma hanno in comune il triangolo
PQV, in cui V è l’intersezione del lati PT ed RQ.
I triangoli SPT e RQZ sono sempre congruenti per il primo criterio
I quadrilateri SPVR e VQZT sono equivalenti perché differenze di figure equivalenti,
ottenute togliendo lo stesso triangolo RVT ai due triangoli congruenti. Essendo
PQRS ≅ SPVR + PQV e PQZT ≅ VQZT + PQV risulta che PQRS ≐ PQZT. c.v.d.
Corollario Ogni parallelogrammo è equivalente a un rettangolo con base ed altezza
congruenti a quelle del parallelogrammo.
2° CASO
Un triangolo ed un parallelogrammo sono equivalenti se hanno le basi congruenti e
se l’altezza del triangolo è doppia di quella del parallelogrammo.
C
Per la dimostrazione è opportuno costruire
il parallelogrammo ABMN con la base AB
in comune con il triangolo ABC e l’altezza
N
R
M G
F
RB congruente alla metà di quella del
triangolo dato.
C
Essendo, per ipotesi, GH ≅ RB, la metà A
B
D H
E
di BC, R è il punto medio di BC ed N lo è di AC.
Il segmento NR che congiunge i punti medi di due lati del triangolo è allora congruente
alla metà del terzo lato, cioè NR ≅ ½ AB.
46
Essendo AB ≅ NM, risulta NR ≅ RM e quindi i triangoli NRC e BMR sono congruenti
per il 1° criterio, avendo: NRC ≅ BRM perché angoli opposti al vertice, e NR ≅ RM e
CR ≅ RB per quanto detto prima.
Poiché ABC ≅ ABRN + NRC e ABMN ≅ ABRN + BMR, risulta ABC ≐ ABMN perché
equiscomponibili ed inoltre, ABMN e DEFG, avendo le basi e le altezze congruenti, sono
equivalenti. ( V. il 1° Caso ).
C.v.d.
Quindi per la proprietà transitiva dell’equivalenza risulta ABC ≐ DEFG.
3° CASO
Un triangolo ed un parallelogrammo sono equivalenti se
hanno le altezze congruenti e se la base del triangolo è
doppia di quella del parallelogrammo.
Osservando la figura si comprende che la dimostrazione è analoga a quella del 2° caso.
4° CASO
Triangoli aventi congruenti la base e le relativa altezza, sono equivalenti
Se il parallelogrammo GHIL
C
F
ha la base congruente a
quella del triangolo ABC e
l’altezza uguale alla metà
L
di CH , per il 2° caso è:
ABC ≐ GHIL.
Anche GHIL ha la base
A
H
B D
E G M
H
congruente a quella del
triangolo DEF e l’altezza pari alla metà di DF, quindi è equivalente a DEF.
Per la proprietà transitiva dell’equivalenza risulta ABC ≐ DEF.
C.v.d.
I
5° CASO
Un trapezio è equivalente a un triangolo avente per base la somma delle basi del
trapezio dato ed altezza congruente a quella del trapezio.
D
C
R
Dato il trapezio ABCD,,per la
dimostrazione si prolunga la
base maggiore AB del trapezio,
di un segmento BE congruente
B
E lla
a DC, che è la base , A
B P
Q
modo che AB + CD = AE
D
C
Le altezze AD e PR sono
congruenti per ipotesi. Si unisce D con E.
F
I triangoli DFC e BEF sono congruenti per
il 2° criterio di uguaglianza dei triangoli perché
A
B
E
47
hanno: DC ≅ BE per costruzione; FDC ≅ FEB perché angoli alterni interni delle rette
parallele AB e DC tagliate dalla trasversale DE; FBE ≅ FCD perché angoli alterni
interni delle stesse parallele, tagliate dalla trasversale CB; quindi ABCD ≐ AED.
Inoltre ADE ≐ PQR perché le basi e le altezze sono congruenti.
Si ha pertanto ABCD ≐ PQR per la proprietò transitiva dell’uguaglianza.
C.v.d.
6° CASO
Un poligono circoscritto ad una circonferenza è equivalente a un triangolo avente
per base il perimetro del poligono e altezza congruente all’apotema del poligono
dato.
Unendo il centro O della circonferenza inscritta, con i vertici del poligono, che In figura è
rappresentato da un quadrilatero, si ottengono quattro triangoli, aventi ognuno per base un
lato del poligono e per altezza
D
C
O
l’apotema OH.
Si costruisce il triangolo A’E’O’
O
con altezza O’H’ ≅ OH e base
B A’
B’ H’ C’
D’
E’
A’E’ ≅ A’B’ + B’C’ + C’D + D’E’ A
H
con A’B’ ≅ AB; B’C’ ≅ D’C;
C’D’ ≅ CD e D’E’ ≅ DA. Se gli estremi di questi segmenti vengono uniti ad O’ si
ottengono quattro triangoli, tutti di altezza O’H’ e base congruente a un lato di ABCD.
I triangoli in cui il quadrilatero ed il triangolo sono stati scomposti sono a due a due
equivalenti, avendo basi ed altezze congruenti.
Si può quindi concludere che
ABCD ≐ A’E’O’ perché somme di superfici equivalenti.
C.v.d.
3.96
Tasformazione di poligoni
Nei casi esaminati nel precedente § si è constatato che ogni parallelogrammo, ogni
trapezio e ogni poligono circoscrittibile si può trasformare in un triangolo o un
rettangolo equivalente.
In realtà questa trasformazione può essere realizzata per qualunque poligono, anche
quando è dato un lato del triangolo o del rettangolo.
Nei punti seguenti si fa riferimento alle dimostrazioni del § precedente.
A
A) Trasformazione di un poligono convesso in un poligono
ad esso equivalente, ma con un lato in meno.
B
r
F
Dato l’esagono ABCDEF si unisce A con E e quindi per
G
F si conduce la parallela r ad AE. Si prolunga quindi il lato C
DE fino ad incontrare la r in G, ottenendo così il pentagono
E
ABCDG.
D
I triangoli AFE e AGE sono equivalenti perché hanno la base in comune e le altezze
congruenti perché segmenti di perpendicolari compresi tra due parallele.
48
L’esagono ABCDEF ed il pentagono ABCDG, essendo la somma del poligono ABCDE
che è comune, e, rispettivamente, dei triangoli AFE e AGE, sono equivalenti perché
somme di figure equivalenti.
C.v.d.
B)
Trasformazione di un poligono convesso in un triangolo ad esso equivalente.
Qualunque poligono convesso può essere trasformato in un triangolo mediante successive
ripetizioni della costruzione descritta nel punto precedente.
C)
Trasformazione di un poligono convesso in un rettangolo ad esso equivalente.
Si trasforma innanzitutto il poligono in un triangolo, poi si costruisce il rettangolo con la
base congruente a un lato del triangolo e l’altezza congruente alla metà di quella del
triangolo relativa a quel lato, oppure con la base congruente alla metà di un lato del
triangolo e l’altezza congruente a quella del triangolo relativa a quel lato.
D)
Trasformazione di un triangolo in un altro equivalente con un lato dato.
E
Dato il triangolo ABC, per costruire un altro
triangolo ad esso equivalente ma con un lato
C
C
congruente ad un segmento dato MN, si porta
sul lato AB del triangolo un segmento AD
E
congruente con MN. Il punto D può venire a
trovarsi all’interno o all’esterno di AB.
In entrambi i casi si unisce C con D e quindi
si conduce per B la parallela r a CD che
A
D
B A
B
D
incontra il lato AC in E.
Congiungendo E con D si ottiene il triangolo
M
N
M
N
ADE che è equivalente a quello dato perché:
--se AB > MN, i triangoli ABC e ADE sono equivalenti essendo composti dal triangolo
ADC in comune e, rispettivamente, dai triangoli CDB e CDE che sono equivalenti
avendo la base in comune e le altezze congruenti (distanze tra rette parallele).
--se AB < MN, i triangoli ABC e ADE sono equivalenti essendo composti dal triangolo
ABE in comune e, rispettivamente, dai triangoloi EBC e EBD che sono equivalenti
avendo la base in comune e le altezze congruenti (V. sopra)
c.v.d
E)
Trasformazione di un triangolo in un altro equivalente avente un’altezza data.
La dimostrazione è analoga a quella del punto 4).
F)
Trasformazione di un qualsiasi poligono in un triangolo ad esso equivalente
avente un lato dato.
SI deve trasformare più volte il poligono in uno equivalente con un lato in meno fino ad
ottenere un triangolo (V. punto 2) e poi si trasforma quest’ultimo in un altro con lato,
oppure altezza, congruenti al lato dato,(V. punti 4 e 5).
G)
Trasformazione di un qualsiasi poligono in un rettangolo di data base, ad esso
equivalente, con la base o l’altezza congruenti ad un segmento dato.
49
Ad es. per trasformare un poligono in un rettangolo di data base ad esso equivalente, si
trasforma il poligono in un triangolo con un lato dato pari alla base del rettangolo e poi
costruire l’altezza del rettangolo congruente a metà dell’altezza del triangolo.
3.97
I TEOREMI DI EUCLIDE E DI PITAGORA
3.97.1
Primo teorema di Euclide
L
In ogni triangolo rettangolo il quadrato costruito
su un cateto è equivalente ad un rettangolo avente
i lati rispettivamente congruenti all’ipotenusa e alla
proiezione ortogonale di quel cateto sull’ipotenusa.
M
D
Ipotesi: AC ⊥ BC; CH ⊥ AB; AB ≅ AF
.
AB ⊥ AF; EA ≅ AC; EA ⊥ AC;
Tesi:
ACDE ≐ AFGH
C
E
M
Dimostrazione:
A
H
B
Dato il triangolo rettangolo ABC ed il rettangolo,
AFGH, si prolungano i lati AF e GH fino ad
incontrare, rispettivamente in M ed in L, il
prolungamento di ED.
I triangoli rettangoli ABC e AME sono congruenti
perché hanno:
.
AC ≅ EA perché lati dello stesso quadrato;
F
G
CAB ≡ EAM perché angoli complementari dello stesso angolo MAC (V. § 3.35)
Segue, in particolare, che AB ≡ AM.
Per la proprietà transitiva della congruenza si ha allora: AF ≅ AM.
Il rettangolo AFGH è quindi equivalente al parallelogrammo ACLM, perché hanno le
basi congruenti e la stessa altezza AH. Anche il quadrato ACDE è equivalente al
parallelogrammo ACLM perché hanno la stessa base AC e la stessa altezza CD.
Si può perciò concludere che, per la proprietà transitiva dell’equivalenza, il quadrato
ACDE è equivalente al rettangolo AFGH.
C.v.d.
3.97.2
Teorema di Pitagora
In ogni triangolo rettangolo il quadrato costruito sull’ipotenusa è equivalente alla
somma dei quadrati costruiti sui cateti.
.
Ipotesi: AC ⊥ BC;
ACFG, BDEC, AHLB sono dei quadrati.
Tesi
AHLB ≡ ACGFG + BDEC
50
Dimostrazione:
E
Dal vertice C del triangolo ABC si conduce la
perpendicolare all’ipotenusa AB, che incontra AB
in M e HL in I.
Per il primo teorema di Euclide è: ACFG ≐ AHIM
e BDEC ≐ MILB.
F
C
G
A
Sommando membro a membro si ottiene:
ACFG + BDEC ≐ AHIM + MILB.
Ma la somma dei rettangoli AHIM + MILB
è il quadrato AHLB e quindi, per la proprietà
transitiva dell’equivalenza si può scrivere
AHLB ≐ ACFG + BDEC.
C.v.d.
3.97.3
D
M
H
B
I
L
Secondo teorema di Euclide
In ogni triangolo rettangolo il quadrato costruito sull’altezza relativa all’ipotenusa è
equivalente al rettangolo i cui lati sono congruenti alle proiezioni ortogonali dei
cateti sull’ipotenusa.
Ipotesi: AC ⊥ BC; CH ⊥ AB
D
CHLM è un quadrato;
Tesi:
C
M
A
H
L
F
N
CHLM ≐ AFGH
E
Dimostrazione:
Sui cateti del triangolo rettangolo AHC si
costruiscono i quadrati AFNH e ACDE.
Per il teorema di Pitagora applicato al
triangolo AHC è:
ACDE ≐ AFNH + CHLM.
Per il primo teorema di Euclide applicato
al triangolo ABC si ha:
ACDE ≐ AGIH.
Il rettangolo AGIH è composto dal quadrato
AFNH e dal rettangolo FGIN.
Si può perciò scrivere AGIH ≐ AFNH + FGIN.
Per la proprietà transitiva dell’equivalenza si ha:
AFNH + CHLM ≐ AFNH + FGIN,
da cui si ottiene
CHLM ≐ FGIN.
3.97.4
B
C,v,d.
Una applicazione del primo teorema di Euclide
Trasformazione di un rettangolo in un quadrato ad esso equivalente.
51
Dato il rettangolo ABCD si costruisce sul
P
lato CD una semicirconferenza di diametro
CD, esterna al rettangolo.
Su CD si prende un segmento DM
congruente ad AD. La perpendicolare ad AD
N
condotta per M incontra la semicirconferenza Q
in N. Congiungendo N con D e con C si
ottiene il triangolo DCN che è rettangolo
perché inscritto in una semicirconferenza
( V. § 3.82)
Il cateto DN è il lato del
D
M
C
quadrato DNPQ equivalente al rettangolo
dato.
Infatti il rettangolo ABCD ha per base
l’ipotenusa DC del triangolo DCN e per
A
B
altezza il segmento AD congruente, per
costruzione, a DM, che è la proiezione ortogonale di DN su DC Quindi per il primo
teorema di Euclide è ABCD ≐ DNPQ.
Si può quindi affermare che ogni poligono, potendo essere trasformato in un rettangolo ad
esso equivalente ( V. § 3.96 C, ) può pure essere trasformato in un quadrato ad esso
equivalente..
3.98
LA MISURA
La teoria della misura ha il compito di associare ad ogni elemento di un dato insieme di
figure (e quindi di grandezze) uno ed un solo numero reale, non negativo, che ne
rappresenta la misura, in modo che siano rispettate determinate proprietà.
Per ragioni di semplicità vengono presi in considerazione i segmenti, già trattati in
precedenza.
Per effettuare una misurazione su un segmento si deve:
1) Fare un confronto (V. § 3.13) allo scopo di stabilire se un certo segmento è
maggiore, minore o uguale ad un altro segmento, non nullo, che viene detto unità di
misura.
2) Avere la nozione di multiplo di un segmento ( V. § 3.16).
3) Stabilire che cosa è un’operazione di addizione, cioè la somma di due o più segmenti
( V. § 3.14).
4) Verificare che esista un sottomultiplo dell’unità di misura che sia contenuto un
numero esatto di volte nel segmento da misurare.
Le quattro proprietà sopraelencate si possono riassumere dicendo che l’insieme dei
segmenti è un insieme di figure omogenee e misurabili.
L’omogeneità dice se è possibile confrontare e addzionare tra loro qualsiasi coppia di
segmenti (proprietà 1 e 2).
La misurabilità si riferisce alle altre due proprietà.
Si può così definire il prodotto di un segmento per un numero razionale assoluto.
Se a è un segmento ed m/n un numero non negativo, si ha
(m/n) a = 0 se a = 0;
(m/n) a = m(a/m) se a ≠ 0.
Si possono fare analoghe considerazioni per gli angoli.
3.99 GRANDEZZE OMOGENEE, MISURABILI E CONTINUE
52
3.99.1
Lunghezze
Nel § 2,4 è stato detto che una relazione di equivalenza è tale se, e solo se, gode
delle tre proprietà: riflessiva, simmetrica e transitiva.
Ad ogni relazione di equivalenza in un insieme non vuoto F , corrisponde una partizione
di F in classi di equivalenza ( V. § 2.18).
La relazione di congruenza è una relazione di equivalenza.
Se si considera l’insieme dei segmenti del piano si può dire che la relazione a ≐ b
è una relazione di equivalenza che permette di dividere il suddetto insieme dei segmenti in
classi di segmenti congruenti tra loro, cioè di realizzare una partizione di tale insieme
Queste classi si chiamano lunghezze per cui si può dire che si chiama lunghezza ogni
classe di equivalenza di segmenti congruenti tra loro.
Pertanto i segmenti congruenti hanno la stessa lunghezza e, viceversa, i segmenti aventi
la stessa lunghezza sono congruenti.
Nell’insieme delle lunghezze si possono definire le quattro proprietà elencate nel
precedente §
La misura delle lunghezze gode delle stesse proprietà della misura dei segmenti, in
particolare quella della continuità: data una lunghezza non nulla u e un numero reale r,
esiste sempre una ed una sola lunghezza a tale che a = r u.
Concludendo si può affermare che:
esiste una corrispondenza biunivoca tra le lunghezze ed i numeri reali non negativi
e: l’insieme delle lunghezze è una clase di grandezze omogenee, misurabii e
continue.
3.99.2
Altre classi di grandezze omogenee e misurabili
Tutto ciò che si è detto nel precedente § a proposito dei segmenti, può essere ripetuto
anche per altri insiemi di figure geometriche, quali ad es. gli angoli del piano, i poligoni
del piano. gli archi di una stessa circonferenza, i settori di uno stesso cerchio.
Le lunghezze dei segmenti sono, come si è visto, il primo esempio di concetto di
grandezza.
Se F è un insieme di figure geometriche ed in esso esiste una relazione di equivalenza,si
può dividere tale insieme in classi di equivalenza, ognuna delle quali si definisce
grandezza geometrica.
Se il suddetto insieme gode delle stesse proprietà dell’insieme delle lunghezze, si dice che
è una classe di grandezze omogenee, misurabili e continue.
Esempi di classi di grandezze sono le ampiezze degli angoli, le estensioni dei poligoni,…
3.100
3.100.1
PROPORZIONALITÀ
Rapporto tra due grandezze
53
Il concetto di misura permette di introdurre la nozione di rapporto tra due grandezze,
purché esse siano omogenee e misurabili..
Se A e B sono due grandezze geometriche, omogenee e misurabili (con B ≠ 0) il
rapporto k tra A e B è la misura di A rispetto a B (considerato come unità di
misura), in cui k è un numero reale assoluto.
Si può quindi scrivere:
A/B = k
⇔
A=kB
Se A, B e U sono tre grandezze omogenee e misurabili, (con B ≠ 0 e U ≠ 0) ed r ed
s sono le misure di A e di B rispetto ad U, risulta:
A/B = r / s
(1)
Infatti se A/B = k, cioè A = k B e per l’ipotesi A = r U e B = s U, con la sostituzione
nella (1) si ottiene: r U = k (s U) e per la proprietà associativa r U = (k s) U, da cui
r = k s . Essendo inoltre B ≠ 0 è anche s ≠ 0 e quindi si può scrivere k = r/s, che è ciò
che si intendeva dimostrare.
Il che significa che il rapporto tra due grandezze è uguale al rapporto tta le rispettive
misure, fatte rispetto ad una medesima unità di misura.
3.100.2
Proporzionalità tra grandezze geometriche
Il rapporto tra grandezze geometriche, omogenee e misurabili, a cui è dedicato il
precedente §, permette di introdurre il concetto di proporzione tra quattro grandezze,
riconducendo le proprietà a quelle dei numeri naturali positivi, in modo da operare sulle
misure delle grandezze anziché sulle grandezze stesse.
Nel seguito vengono considerate solo grandezze diverse da zero.
Si dice che quattro grandezze A, B, C, D, nell’ordine, formano una proporzione se i
rapporti A : B e C : D sono uguali tra loro, cioè A/B = C/D.
A,B,C,D, si chiamano termini della proporzione;
A e C sono gli antecedenti;
B e D i conseguenti;
A e D gli estremi;
B e C i medi;
D la quarta proporzionale dopo A, B e C.
Una proporzione in cui i medi sono uguali è detta continua. In questo caso B è la media
proporzionale ( o media geometrica) tra A e C; e C è la terza proporzionale dopo
A e B.
Considerando, anziché le grandezze, le relative misure, a, b, c, d, tutti numeri
positivi, si può dire che esse, nell’ordine, formano una proporzione se sono uguali
tra loro i rapporti a/b e c/d.
Si può dimostrare che quattro grandezze, di cui le prime due omogenee tra loro e le
altre due pure omogenee tra loro, sono in proporzione se, e solo se, lo sono le loro
misure.
Infatti, poichè il rapporto tra le grandezze è uguale al rapporto tra le relative misure, come
è stato dimostrato nel precedente §, si ha: A/B = a/b e C/D = c/d per cui, per
ipotesi, da A/B = C/D segue a/b = c/d e viceversa.
54
Se valgono le proporzioni A/B = C/D e a/b = c/d , sono valide anche le proporzoni che
si ottengono:
invertendo: B/A = D/C e b/a = d/c;
permutando: D/B = C/A e d/b = c/a scambiando tra loro gli estremi:
A/C = B/D e a/c = b/d
“
“ “ i medi
D/C = B/A e d/c = b/a scambiandoli entrambi;
componendo: (A + B) / B = (C + D) / D e (a + b) / b = (c + d) / d
sostituendo gli
antecedenti con la loro somma con i rispettivi conseguenti;
scomponendo: (A – B) / B = (C – D) / D e (a - b) / b = (c – d) / d
sostituendo gli
antecedenti con la loro differenza con i rispettivi conseguenti, se A>B, C>D a>b, c>d,
3.100.3
Proporzionalità diretta
Se G e G’ sono due classi di grandezze omogenee e misurabili, si dice che esse sono
(direttamente) proporzionali se esiste, tra G e G’, una corrispondenza biunivoca f
tale che il rapporto tra due grandezze qualunque di G è uguale al rapporto tra le
grandezze corrispondenti di G’. f è detta corrispondenza di proporzionalità diretta
o semplicemente proporzionalità,
Si può dimostrare che:
se due classi di grandezze sono direttamente proporzionali, il rapporto tra la misura
di una qualsiasi grandezza della prima classe e la misura della corrispondente
grandezza della seconda classe è costante. E viceversa.
Infatti, fissate le unità di misura delle due classi, se si indicano con a, b, c, d le misure
delle grandezze A, B, C, D della prima classe, e con a’, b’, c’, d’ le misure delle
grandezze A’, B’, C’, D’ della seconda classe, essendo le due classi proporzionali, si ha.
a/b = a’/b’ ; b/c = b’/c’ ; c/d = c’/d’…..
(1)
dalle quali, permutando i medi, si ottengono le uguaglianze di rapporti numerici:
a/a’ = b/b’ = c/c’ =….. .
(2)
E viceversa: infatti: se è costante il rapporto tra le misure di grandezze corrispondenti
valgono le (2) e quindi le (1) per cui si può concludere che le classi sono direttamente
proporzionali.
Questo rapporto costante si chiama coefficiente costante di proporzinalità.
Se si indica questa costante con k e con y ed x le misure di due grandezze qualunque
corrispondenti delle due classi, dalla (2) si ha
y/x = k da cui y = k x.
Questa espressione si chiama equazione della proporzionalità diretta perché le coppie
ordinate a ed a’, b e b’, c e c’ … che la soddisfano sono tutte e sole le misure delle
coppie di grandezze A ed A’, B e B’ , C e C’ …. che si corrispondono nella
proporzionalità.
3.100.4
Proporzionalità inversa
Se G e G’ sono due classi di grandezze omogenee e misurabili, si dice che G e G’
sono inversamente proporzionali, se esiste una corrispondenza biunivoca f ’ tra G e
G’ tale che il rapporto tra due grandezze, non nulle, qualsiasi di G è uguale all’inverso del
rapporto tra le grandezze corrispondenti di G’. In questo caso f ’ è detto corrispondenza
di proporzionalità inversa.
55
Si quindi affermare: se due classi di grandezze sono inversamente proporzionali
esiste la proporzione A / B = B’ / A’ qualunque siano le grandezze A e B.
Come per le grandezze direttamente proporzionali si può dimostrare che:
se due classi di grandezze sono inversamente proporzionali, il prodotto tra le
misure di una grandezza qualunque della prima classe e la misura della grandezza
corrispondente della seconda classe è costante. E viceversa.
Infatti: se G e G’ sono inversamente proporzionali, valgono le proporzioni numeriche:
a/b = b’/a’ ; b/c = c’/b’ ; c/d = d’/c’
da cui, moltiplicando ambo I membri, rispettivamente, per a’ b , b’ c, c’ d, si ottiene
a a’ = b b’ = c c’ = d d’
e quindi, indicando con k il valore comune di tali prodotti, si ha:
a = k/a’; b = k/b’; c = k/c’; d = k/d’.
Se si indicano con x e y le misure di una grandezza A, non nulla, di G e della
corrispondente grandezza A’ di G’, si può scrivere:
y = k/x
o anche
xy = k
Questa espressione è l’equazione della prorzionalità inversa.
3.101
Misura dei segmenti
Scelto arbitrariamente un segmento come unità di misura, (U = 1), cioè come segmento
unitario, se si confronta un segmento dato AB con
U
il segmento unitario, il numero che indica quante volte
AB contiene U oppure ne è contenuto, si dice misura
A
B
del segmento dato.
Se ad es. CD contiene 5 volte U si scrive CD = 5.
Generalmente si sceglie come unità di misura delle lunghezze il metro ( abbreviato in m )
o un suo multiplo, ad es il chilometro ( abbrev. In km ) oppure un sottomultiplo, ad es. il
centimetro ( abbrev. in cm ).
Una riga, lunga di solito 50 cm, è normalmente divisa, con delle incisioni equidistanti, in
50 parti, lunghe 1 cm ciascuna, le quali, a loro volta, sono divise in 10 parti uguali, lunghe,
ciascuna, 1 millimetro ( abbrev. mm ).
Per misurare un segmento AB mediante una riga graduata, si dispone il trattino della
graduazione corrispondente allo zero sull’estremo A del segmento, si fa coincidere il
bordo della riga con il segmento e si legge sulla riga il valore che corrisponde all’estremo
B. Questo valore è la misura o lunghezza di A.
Se ad es. B cade in corrispondenza della graduazione 25,6 si conclude che AB è lungo
25.6 cm, ossia 256 mm.
3.102
Misure degli angoli
Analogamente a quanto è stato fatto per i segmenti, per misurare un angolo occorre
stabilire una unità di misura degli angoli, con la quale gli angoli da misurare si devono
confrontare. L’unità di misura degli angoli, di maggiore impiego, è il grado (simbolo °)
che è la 90a parte dell’angolo retto, la 180a parte dell’angolo piatto, la 360a parte
dell’angolo giro.
I sottomultipli del grado sono il primo (simbolo ‘ ) che è la 60a parte del grado ed il
secondo (simbolo ‘’ ) che è la 60a parte del primo e quindi la 3600a parte del grado.
Ci sono poi ancora altri sottomultipli, usati in misure di precisione, che sono i decimi ed i
centesimi di secondo.
56
La misura di un angolo, che ne dà l’ampiezza, è il numero che indica quante volte il grado,
o un suo sottomultiplo, sono contenuti nell’angolo dato.
Se, ad es. l’angolo ha una ampiezza di 13 gradi, 25 primi, e 15 secondi tale misura si
scrive 13° 25’ 15’’. Questa è la forma normale con cui si indica la misura di un angolo.
3.103
Operazioni sulle misure degli angoli
Non è normale la forma della misura di un angolo in cui i primi ed i secondi hanno valori
maggiori di 60.
Se ad es. la misura di un angolo è 45° 135’ 75’’. t ale forma non è normale. Si deve quindi
trasformare la misura suddetta in forma normale. Per fare questa trasformazione,
ricordando che 1° = 60’, 1’ = 60’’, si deve sottra rre al numero che indica i secondi tante
volte 60 quanto è possibile: 75’’ – 60 = 15’’. Lo stesso si deve fare con il numero dei primi,
dopo aver aggiunto ad essi i primi, sottratti ai secondi: nel caso dell’esempio soltanto 1.
Quindi si ha: 135’ + 1’ = 136’, 136’ - 2• 60 = 16’. Infine si aggiungono ai gradi i 2° t olti
ai primi e si ottiene così il valore della misura, ridotta in forma normale, che è 47° 16’ 15’’
3.104
Addizione
Per effettuare la somma delle misure di due o più angoli, si dispongono tali misure, detti
addendi, in tre colonne, gradi, primi e secondi e si fa la loro somma, colonna per colonna,
come in una normale addizione di numeri.
=
45°
37°
15°
97°
3.105
15’ 35’’ +
25’ 17’’ +
22’ 55’’
62’ 107’’ che, ridotta in forma norma le, diventa 98° 3’ 47’
Sottrazione
Per effettuare la differenza tra le misure di due angoli, di cui il primo, minuendo, maggiore
del secondo, sottraendo, si deve disporre le misure in tre colonne, gradi, primi, secondi e
fare le differenze, colonna per colonna
64° 37’ 25’’ – (minuendo)
45° 25’ 17’’
(sottraendo)
= 19° 12’ 8’’
(differenza)
Nel caso che i valori dei primi e/o dei secondi del sottraendo siano superiori ai
corrispondenti valori del minuendo, si deve operare nel modo seguente.
Si sottrae 1° al numero dei gradi del minuendo : 37° - 1° = 36° Si somma questo grado,
trasformato in 60’, al numero dei primi, sempre del minuendo: 25’ + 60’ = 85’. Infine si
sottrae 1’ a quest’ultimo numero dei primi e lo si aggiunge, trasformato in 60’’,al
numero dei secondi della misura data: 17’’+ 60’’= 77’’. Si ottiene così la misura nella forma
che permette di effettuare la differenza.
36° 84’ 77’’ –
25° 38’ 45’’
= 11° 46’ 32’’
57
3.106
Moltiplicazione per un numero intero
La moltiplicazione della misura di un angolo per un numero intero si effettua moltiplicando
per quel numero, separatamente, i gradi, i primi ed i secondi, riducendo poi, se
necessario, il risultato, in forma normale.
45° 15’ 35’’ x
5
= 225° 75’ 175’’ (175’’ – 120’’ = 55’’ ; 77’ – 60’ = 17’ ; 225° + 1° = 226° )
Il risultato della moltiplicazione, ridotto in forma normale, è quindi:
3.107
226° 17’ 55’’
Divisione per un numero intero
Per dividere la misura di un angolo per un numero intero, si dividono per tale numero,
prima i gradi. Il resto di questa divisione si trasforma in primi (moltiplicandolo per 60) e si
sommano questi primi a quelli della misura data. Si effettua quindi la divisione del numero
totale dei primi, così ottenuto, per il divisore e poi si trasforma il resto in secondi
(moltiplicando ancora per 60) che si sommano ai secondi della misura data. Il numero
totale dei secondi viene, a sua volta, diviso per il divisore. L’eventuale resto di quest’ultima
divisione fornisce i decimi ed i centesimi di secondo.
45° 39’
27’’ : 4
1° = 60’
11° 24’ 51’’,75
99’
3’ = 180’’
207’’
3’’
3.108
Moltiplicazione per una frazione
Per effettuare la moltiplicazione della misura di un angolo per una frazione, come, ad es.
3/5, si divide tale misura per il denominatore della frazione e poi si moltiplica il risultato
ottenuto per il numeratore, operando come descritto nei §§ precedenti.
27° 39’
23’’ : 5
2° = 120’
5° 31’ 52’’,6 x
159’
3
4’ = 240’’ 15° 93’ 157’’,8 che , ridotto i forma normale, diventa 16° 35’ 37’’,8
263’’
3’’
3.109 FORMULE PER IL CALCOLO DELL’AREA DI UN POLIGONO
Per il calcolo dell’area di un poligono si sceglie arbitrariamente come
unità di misura un quadrato di lato unitario u, la cui superficie
misura 1, ossia l’area è 1.
Tale quadrato, indicato con U, è l’unità di misura delle superfici.
58
u
U
u
3.110
Area del rettangolo
La misura della superficie di un rettangolo rispetto ad U è il numero dato dal
rapporto tra la superficie del rettangolo ed U.
Seguono alcuni esempi di calcolo della superficie
di un rettangolo:
1) Dato un rettangolo la cui base misura 5 u e
l’altezza 2 u, osservando la figura si vede che
il suddetto rettangolo è composto da 10 U.
Quindi la sua area è 10 = 2• 5 cioè è uguale semplicemente al prodotto della
misura della base per quella dell’altezza.
2) Se il rettangolo di cui si vuole misurare l’area
ha la base che misura 6/5 u e l’altezza che 1/3 u
misura 5/3 u, se lo si scompone in tanti
rettangolini aventi i lati di u/5 e u/3, se ne
ottengono 30.
Essendo l’area di tali rettangolini uguale a
u/3 • u/5 = U/15, l’area del rettangolo dato
risulta (U/15) 30 = 2U cioè 2, che è il
1/5 u
risultato del prodotto di (6/5)(5/3) = 30/15 = 2
Anche in questo caso l’area è uguale al prodotto delle due dimensioni del rettangolo.
3) Per determinare l’area di un rettangolo di lati 3 u e √2 u, essendo √2 un numero
Irrazionale, si deve ricorrere ad una approssimazione.
Poiché il valore di √2 è 1,4142135…cioè compreso tra 2 e 3, l’area del rettangolo
sarà maggiore di 3 • 2 = 6 e minore di 3 • 3 = 9
Volendo una maggiore approssimazione si possono considerare i valori della radice
compresi tra 1,41 e 1,42 e poi tra 1,414 e 1,415 e così via.
Considerando accettabili gli ultimi valori l’area risulterebbe compresa tra 4,242 e
4,245. Procedendo in questo modo si giunge alla conclusione che che l’area del
rettangolo dato è espressa dal numero irrazionale 3 √2, che è di nuovo uguale al
prodotto delle dimensioni del rettangolo.
Si può quindi affermare che la misura della superficie di un rettangolo si calcola
moltiplicando la misura della base per quella dell’altezza, cioè, indicando con
b e h tali misure la formula per il calcolo dell’area di un rettangolo è
A = b h.
3.111
Area del quadrato
Il quadrato non è altro che un rettangolo con la base uguale all’altezza = l e quindi
la formula per il calcolo dell’ area del quadrato è
A = l 2..
3.112 Area del parallelogrammo.
Si è visto in precedenza (V. § 3.95 1° caso) che ogni parallelogrammo è equivalente ad
un rettangolo con la base e l’altezza congruenti a quelle del parallelogrammo, per cui,
indicando con b ed h le misure delle sue dimensioni la formula per il calcolo dell’area
del parallelogrammo è uguale a quella del rettangolo, cioè
A = bh
59
3.113
Area del rombo
Poiché ogni rombo è equivalente ad un rettangolo con un
lato congruente ad una diagonale del rombo e l’altro lato
pari alla metà dell’altra diagonale del rombo, la formula
per il calcolo dell’area del rombo è
A = dD/2
3.114
Area del triangolo
Come è noto (V. § 3.95 3° caso), ogni triangolo è equivalente ad un rettangolo avente
la base (o l’altezza) congruente a quella del triangolo e l’altezza (o la base) pari alla metà
di quella del triangolo. Indicando con b e h le misure della base del triangolo e
dell’altezza ad essa relativa, la formula per il calcolo dell’area del triangolo è
A = bh/2
3.115
Misura dell’altezza relativa all’ipotenusa di un triangolo rettangolo
L’area di un triangolo rettangolo si può calcolare in due modi diversi Cioè:
1) prendendo come base l’ipotenusa e
considerando l’altezza ad esso relativa, .
2) prendendo come base un cateto e
considerando come altezza l’altro cateto.
c
b
b
a
Nel primo caso la formula per il calcolo
h
dell’area del triangolo rettangolo risulta
A = a h/ 2,
a
c
Nel secondo caso
A = b c/2.
Uguagliando i secondi membri si ha a h/2 = b c/2 da cui si ottiene a h = b c e quindi
h = bc/a
che è la misura dell’altezza relativa all’ipotenusa.
Si può quindi concludere che in un triangolo rettangolo l’altezza relativa all’ipotenusa
è uguale al quoziente tra il prodotto delle misure dei cateti e quella dell’ipotenusa.
3.116
Formula di Erone per calcolare l’area di un triangolo qualsiasi, note le
misure dei suoi lati
Se si indicano con a, b, c le misure dei lati di un triangolo qualunque e con p la misura
del semiperimetro, la formula di Erone per il calcolo dell’area del triangolo è:
A = √ p (p - a) (p - b) (p - c)
3.117 Area del trapezio
Poiché ogni trapezio è equivalente ad un triangolo con la base congruente alla somma
delle basi del trapezio e l’altezza congruente a quella del trapezio (V. § 3.95 5° caso)
indicando con b e B le basi, rispettivamente, minore e maggiore del trapezio e con h
l’altezza, la formula per il calclolo dell’area del trapezio è:
A = (b + B) h / 2
60
3.118
Area di un poligono circoscritto ad una circonferenza
Un poligono qualunque circoscritto ad una circonferenza è equivalente a un triangolo con
la base congruente al perimetro del poligono (V. § 3.95
6° caso ) e l’altezza congruente al raggio della circonferenza,
che è l’apotema del poligono.
Poiché un triangolo è equivalente ad un rettangolo con la
base congruente e l’altezza pari alla metà di quella del
O
triangolo, indicando con 2p la misura del perimetro del
r
poligono e con r il raggio della circonferenza, la formula
per il calcolo dell’area del poligono è:
A = 2pr/2 = pr
Questa formula è valida anche per il calcolo dell’area di un poligono regolare, che è
sempre circoscrittibile.
3.119
Misura del raggio della circonferenza inscritta in un poligono
Poiché un triangolo è sempre circoscrittibile a una circonferenza si può calcolarne l’area
mediante la formula A = p r del § precedente, dalla quale si può, conoscendo area e
semiperimetro del triangolo, calcolare il raggio della circonferenza inscritta che è:
r = A/p
In generale si può affermare che il raggio della circonferenza inscritta in un poligono è
il rapporto tra l’area e la misura del semiperimetro del poligono.
3.120
Misura del raggio della circonferenza inscritta in un triangolo rettangolo
Per il calcolo del raggio della circonferenza inscritta in
C
un triangolo rettangolo si può adottare anche un’altra
K
formula.
R
b
Dato il triangolo rettangolo ABC circoscritto alla
c
O
circonferenza di centro O e raggio r, se si tracciano
i raggi perpendicolari ai lati del triangolo, che incontrano
la circonferenza nei punti di tangenza, si constata che il A
H
B
quadrilatero OKCR è un quadrato con il lato congruente
a
al raggio della circonferenza inscritta.
Inoltre AR ≅ AH e HB ≅ BK perché segmenti di tangente.( V. § 3.86)
Se si indicano con a, b, c le misure dei lati del triangolo e con r la misura del raggio
della circonferenza, si può scrivere:
AH = AR = AC – RB = c – r
e
HB = BK = B C - CK = b - r
Poiché AB ≅ AH + HB
si ha a = (c – r) + (b –r) = (c + b) – 2 r
e quindi
r = (c + b) – a / 2
Si può concludere affermando che la misura del raggio della circonferenza inscritta in
un triangolo rettangolo è la metà della differenza tra la somma dei cateti e
l’ipotenusa.
3.121
RIFORMULAZIONE DEI TEOREMI DI PITAGORA E DI EUCLIDE
61
Dal momento che adesso si è in grado di calcolare le misure dei segmenti, si possono
riformulare i teoremi di Pitagora e di Euclide, adottando le misure anziché le figure
geometriche.
3.122
Teorema di Pitagora
In ogni triangolo rettangolo l’area del quadrato avente come lato l’ipotenusa è
uguale alla somma delle aree dei quadrati che hanno come lati i cateti
Se si indicano con a, b, e c, rispettivamente, le misure dell’ipotenusa e dei cateti di un
qualsiasi triangolo rettangolo, si può esprimere il suddetto teorema con la formula:
a2 .= b2 + c2
Mediante tale formula è possibile calcolare qualsiasi lato di un triangolo rettangolo quando
siano noti gli altri due:
a = √ b2 + c2;
b = √ a2 - c2;
c = √ a2 - b2
3.123
Primo teorema di Euclide
In ogni triangolo rettangolo l’area del quadrato avente come lato un cateto è uguale
all’area del rettangolo che ha come lati l’ipotenusa e la proiezione ortogonale dello
stesso cateto sull’ipotenusa.
Se si indicano con a, b, e c, rispettivamente, le misure dell’ipotenusa e dei cateti di un
triangolo rettangolo e con m ed n le proiezioni ortogonali, rispettivamente, di c e di b,
sull’ipotenusa, si può esprimere il suddetto teorema mediante le formule:
c2 = m a
e
b2 = n a
Per mezzo di tali formule si possono calcolare:
c = √ma
b = √mb
m c2 / a
n = b2 / a
a = c2 / m = b2 / n
3.124
Secondo teorema di Euclide
In ogni triangolo rettangolo l’area del quadrato che ha come lato l’altezza relativa
all’ipotenusa è uguale all’area del rettangolo che come lati le proiezioni ortogonali
dei cateti sull’ipotenusa
Se si indicano con a, b, e c, rispettivamente, le misure dell’ipotenusa e dei cateti, con h
la misura dell’altezza relativa all’ipotenusa e con m ed n le misure delle proiezioni
ortogonali, rispettivamente, di c e di b, sull’ipotenusa, il teorema suddetto può essere
espresso con la formula:
h2 = m n
dalla quale si può ricavare:
h = √mn
m = h2 / m = h2 / n
62
3.125
Applicazioni del teorema di Pitagora
Le formule espresse nei precedenti §§ consentono di risolvere molti problemi di geometria
nei quali siano presenti dei triangoli rettangoli
3.126
Misura della diagonale di un quadrato in funzione del lato
Se si indicano con l e d, rispettivamente, il lato di un quadrato ed una sua diagonale che
lo divide in due triangoli rettangoli isosceli, tra loro congruenti, applicando il teorema di
Pitagora ad uno di tali triangoli si ottiene:
d2 = l 2 + l 2 = 2 l 2
Con tale formula si possono ricavare:
d = √2 l
l = d/√2
3.127
Misure dei lati di un triangolo rettangolo isoscele
Un triangolo rettangolo isoscele ha gli angoli alla base, tra loro congruenti, di 45° ( metà
dell’angolo retto). Anche di 45° sono gli angoli formati, ognuno dalla
diagonale e da un lato l di un quadrato che sono, rispettivamente,
l’ipotenusa e un cateto di uno dei due triangoli rettangoli isosceli
c
in cui la diagonale divide il quadrato. Indicando con i la misura
della diagonale del quadrato, cioè dell’ipotenusa del triangolo e
con c la misura del lato del quadrato, cioè del cateto del triangolo,
i
si ottiene:
i = √2 c (V. § precedente)
c = i / √2 = √ 2 i / 2
3.128
Misura dell’altezza di un triangolo equilatero in funzione del lato
In un triangolo equilatero di lato l, l’altezza h relativa ad un lato,
preso come base, divide il triangolo dato in due triangoli rettangoli
di cui le misure dei cateti sono h ed l / 2 e la misura dell’ipotenusa
è l.
Applicando il teorema di Pitagora ad uno dei due triangoli si ottiene:
l 2 = (l / 2)2 + h2
h
l/2
da cui si può ricavare
h = √ l 2 - l 2/ 4 = √ 3 l 2 / 4 = √ 3 l / 2
l = 2h/√3 = 2√3 h/3
63
l
l/2
3.129
Misure dei lati di un triangolo rettangolo con gli angoli acuti di 30° e 60°
in un triangolo equilatero (ed equiangolo), i cui angoli sono tutti
di 60°, l’altezza relativa alla base divide il tri angolo stesso in
due triangoli rettangoli in cui gli angoli acuti sono di 30° e 60°
e l’altezza suddetta è uno dei cateti, indicata con a, mentre il
lato del triangolo dato i è l’ipotenusa e la proiezione ortogonale
di quest’ultima sulla base è l’altro cateto b.
Dalle formule dei § precedenti si ricava
b = i/2 = √3 a/3
a = √3 i/2 = √3 b
i = 2√3 a/2 = 2b
3. 130
30°
i
a
60°
60°
b
MISURA DELLA CIRCONFERENZA
Per calcolare la misura di una circonferenza si deve trasformarla in un segmento
avente la stessa lunghezza, cioè la si deve rettificare.
A
Per fare questo, però, si devono introdurre i seguenti assiomi:
B
a) Un arco di circonferenza, minore della semicirconferenza,
è maggiore della corda da esso sottesa.
b) Un arco di circonferenza,delimitato dai punti di tangenza
O
delle due tangenti condotte ad essa da un punto esterno
C
alla circonferenza, è minore della somma dei segmenti di
tangenza.
BC < BC < AB + AC
Di conseguenza il perimetro di ogni poligono regolare circoscritto ad una circonferenza è
maggiore della circonferenza e questa, a sua volta, è maggiore
del perimetrro di qualunque poligono regolare inscritto nella
stessa circonferenza.
Se si aumenta il numero dei lati dei due poligoni i loro perimetri
si avvicinano indefinitamente e tendono ad un unico valore che
è la misura della circonferenza rettificata, che è pertanto l’unico
segmento maggiore del perimetro di qualsiasi poligono regolare
inscritto nella circonferenza e minore di qualsiasi poligono regolare
circoscritto alla circonferenza.
Se si prendono in esame due circonferenze, di cui la prima con il diametro doppio di quello
della seconda, e le si misurano nel modo precedentemente descritto, si trova che la
misura della seconda circonferenza è doppia della prima.
Se si considera, ora, una terza circonferenza con il diametro doppio di quello della
seconda, si trova dinuovo che la misura della terza circonferenza è doppia di quella della
seconda. E cosi via.
Indicando con C1, C2, C3 .. le misure delle circonferenze prese in esame, e con
d1, d2, d3,…le misure dei relativi diametri, si può scrivere:
C1 / d1 = C2 / d2 = C3 / d3 =……C / d,
ossia il rapporto tra la misura di una circonferenza e quella del suo diametro è una
costante, cioè è indipendente dalla circonferenza esaminata.
Questa costante è un numero reale, irrazionale, che vale 3,1415926535…….e che
viene simboleggiato con π ( pi greco),
64
Usualmente si dice che π ≈ 3,14 (*)
Si può quindi affermare che i rapporti C / d, prima considerati, sono circa uguali a
3,14, ossia che la misura di una circonferenza di diametro d e raggio r è:
C ≈ 3,14 d ≈ 2 π r
3.131
Lunghezza di un arco di circonferenza
Dal momento che una circonferenza può essere considerata come un arco di 360°,
se si indicano con α°, C ed l l’ampiezza di un arco al centro, la lunghezza della
circonferenza e la lunghezza dell’arco corrispodente all’angolo al centro, si può scrivere la
proporzione:
360° : α° = C : l
da cui si ricava la lunghezza di un arco di circonferenza che è
l = α° C / 360°
3.132
AREA DEL CERCHIO
Anche per calcolare l’area del cerchio vale il ragionamento fatto per il calcolo della
circonferenza.
L’area di un cerchio, infatti, è compresa tra la superficie del poligono circoscritto e
quella del poligono inscritto nel cerchio.
Se si aumenta il numero dei lati dei due poligoni, la differenza tra le loro aree diminuisce
sempre di più ed i loro valori tendono ad un unico limite che rappresenta l’area del cerchio.
L’area del cerchio è l’unica area minore dell’area di ogni poligono circoscritto e maggiore
dell’area di ogni poligono inscritto nel cerchio.
Si può dimostrare che un cerchio è
equivalente ad un triangolo avente la
base congruente alla circonferenza
r
r
rettificata e l’altezza congruente al
raggio del cerchio.
Se si indicano con A, C, ed r l’area del cerchio, la misura della circonferenza e la
misura del raggio si ha:
A = C r / 2 = 2 π r r / 2 = π r2
Quindi l’area del cerchio è
A = π r2
3.133
Area di un settore circolare e area di un segmento circolare
Un cerchio può essere considerato come un settore circolare con angolo al centro di 360°
(*) Una curiosità matematica
E’ quasi impossibile ricordare a memoria molte cifre decimali di pi greco. Tuttavia una frase in francese che,
volendo, si può imparare a memoria, consente di scrivere ben 24 cifre decimali di tale numero. Eccola:
Que j’aime à faire apprendre un nombre util aux sages? Immortel Archimède, artiste, ingenieur,
qui de ton jugement peut priser la valeur?
65
Se si indicano con α°, A, ed S l’ampiezza di un angolo al centro,
l’area del cerchio e l’area del settore circolare, si può scrivere la
proporzione:
360° : α° = A : S
da cui si ottiene l’area del settore circolare che è
S = α° A / 360°
In un cerchio la corda AB lo divide in due segmenti circolari.
L’area del segmento circolare corrispondente all’arco ACB
si può ottenere facendo la differenza tra l’area del settore
circolare corrispondente all’arco suddetto
(di colore
azzurro in figura) e l’area del triangolo AOB
C
A
B
O.
Invece l’area del segmento circolare corrispondente all’arco
ADB si ricava facendo la somma dell’area del settore circolare
corrispondente al suddetto arco ( di colore giallo in figura), più
l’area del triangolo AOB.
3.134
D
LE TRASFORMAZIONI NEL PIANO
Le trasformazioni geometriche nel piano stabiliscono una corrispondenza biunivoca
tra i punti di un piano. Esiste cioè una relazione che fa corrispondere ad ogni punto
del piano uno ed un solo punto dello stesso piano.
Le trasformazioni di questo tipo si chiamano affinità.
Sono affinità: le simmetrie, le traslazioni, le rotazioni, le omotetie e le similitudini.
Le prime tre sono trasformazioni isometriche o isometrie, che sono già state trattate nei
§§ 3.59 e seguenti.
Se in una trasformazione nel piano ad un punto P corrisponde se stesso, P si
chiama punto unito.
Analogamente, se ad una retta del piano corisponde se stessa, tale retta si dice retta
unita.
Studiare una trasformazione significa determinarne il tipo e cercarne gli eventuali elementi
uniti.
3.135
Omotetia
Dato un punto O nel piano ed un numero k reale, non nullo, si chiama omotetia di
centro O e rapporto k la trasformazione nel
piano che fa corrispondere a un punto A del
B’
piano, un puntoA’ dello stesso piano, allineato
k = 3
A’
con O, tale che il rapporto OA’ / OA = k.
Così pure per altri punti, come B e C, ai quali
corrispondono B’ e C’.
B
A
Se k > 0 l’omotetia è diretta;
Se k = 0 l’omotetia è inversa
O
Se k = 1 l’omotetia è l’identità
C’
C
66
Se k = -1 l’omotetia coincide con la simmetria centrale il cui centro è il centro
dell’omotetia.
Sono omotetie l’ingrandimento o il rimpicciolimento di figure geometriche.
L’omotetia ha un unico punto unito che è il suo centro.
Seguono alcuni teoremi:
1- L’omotetia trasforma una retta in una retta ad essa parallela.
Infatti, data una retta r sulla quale sono segnati tre punti A, B, C, se si indicano con A’,
B’, C’, i punti corrispondenti in una omotetia di centro O e rapporto k, per definizione è
OA’ / OA = OB’ / OB = OC’ / OC = |k|
Ricordando quanto è stato esposto nel § 3.100.3, a
O
proposito della proporzione diretta, si può affermare
k = 2
che, essendo OA’, OB’, OC’, direttamente e con lo
stesso rapporto, proporzionali, rispettivamente, ad r
A
B
C
OA, OB, OC, per l’inverso del teorema di Talete
( V. § 3.43) la retta r’, che passa per A’, B’, C’ ,
risulta parallela alla r.
r’ A’
B’
C’
c.v.d
In un’omotetia sono unite le rette passanti per il centro dell’omotetia stessa
2- Angoli che sono corrispondenti in un’omotetia sono congruenti.
A’
Infatti, in un’omotetia di centro O e rapporto k, osservando
A
P
la figura, si vede che: per ipotesi è OA’ / OA = OB’ / OB = |k|,
e per il precedente punto 1, la retta A’B’ è parallela alla retta O
AB.
B
B’
Se dal punto B si conduce la parallela ad AA’, che incontra
A’B’ nel punto P, considerando il triangolo OA’B’ e la retta BP parallela ad OA’, per il
corollario del teorema di Talete che recita: “ Una retta parallela ad un lato di un triangolo e
secante gli altri due lati, divide questi ultimi in segmenti direttamente propozionali ”, si può
scrivere:
OB’ / OB = A’B’ / AB ed essendo OB’ / OB = |k| è pure A’B’ /AB = |k| c.v.d.
3- Due triangoli, non congrenti, sono omotetici se hanno i lati due a due paralleli
3.136
Le equazioni dell’omotetia con centro nell’origine degli assi cartesiani
In un sistema di assi cartesiani xOy sia dato un punto y
P(x;y) Se si appilca l’omotetia di centro O con rapporto
k, per la definizione di omotetia il punto P’, che nella Py
omotetia corrisponde a P, sta sulla semiretta OP ed
è OP’ / OP = |k|
Se si vuole determinare le coordinate di P’ in funzione
di quelle di P, per il teorema di Talete si può scrivere
O
67
P’ (x’;y’)
P (x;y)
Px
P’x
x
(v, la figura):
OP’ / OP = OP’x / OPx = |k|
ed anche
OP’ / OP = OP’y / OPy = |k|’
Utilizzando le coordinate al posto dei segmenti ed eliminando i valori assoluti si ricavano
le formule:
x’ = k x
y’ = k y
’
che sono le equazioni dell’omotetia di centro nell’origine degli assi cartesiani e
rapporto k.
3.137
Similitudine
La similitudine è una trasformazione nel piano che mantiene invariati gli angoli ed
il rapporto tra i segmenti ed è ottenuta come prodotto di una omotetia e di una
isometria (congruenza) o viceversa.
Il suddetto rapporto è detto rapporto di similitudine.
Segmenti o angoli che sono corrispondenti in una similitudine sono detti omologhi.
Se la isometria utilizzata nel prodotto a cui si è accennato sopra è diretta, la similitudine è
diretta, in caso contrario è inversa.
Il simbolo della similitudine è ~
Se F ed F’ sono due figure simili, simbolicamente si scrive F ~ F’.
La similitudine ha le seguenti proprietà:
-
Trasforma le rette in rette (cioè conserva l’allineamento dei punti)
Trasforma gli angoli in angoli congruenti (cioè conserva l’ampiezza degli angoli)
Conserva il parallelismo ( e quindi la perpendicolarità)
Conserva il rapporto tra i segmenti.
Il prodotto (o composizione) di due similitudini è una similitudine.
Se k1 e k2 sono, rispettivamente i rapporti di similitudine delle due similitudini
suddette, il rapporto di similitudine del loro prodotto è k1 k2
L’inverso di una similitudine di rapporto k ha il rapporto 1/k
3.138
Criteri di similitudine dei triangoli
Talvolta è difficile stabilire se due triangoli sono simili. In tali casi sono utili i seguenti
criteri.
3.139
Primo criterio di similitudine dei triangoli
Se due triangoli hanno due coppie di angoli congruenti, sono simili
C
Infatti: dati i triangoli ABC e DEF che hanno
F
congruenti, rispettivamente, gli angoli in C
e in F e gli angoli in A ed in D, hanno
congruenti anche i rimanenti angoli: in B
M
N
ed in E.
Se è anche AC ≅ DF i due triangoli sono
A
B
D
68
E
congruenti e quindi sono simili
Supponendo invece che AC e DF non siano congruenti ma che, ad es., sia AC > DF,
sul lato AC del triangolo ABC si prende un punto tale che MC ≅ DF, poi da M si
conduce la parallela alla base AB del triangolo, che interseca il lato BC nel punto N.
Si ottiene così il triangolo MNC che, per il terzo criterio di congruenza dei triangoli, è
congruente al triangolo DEF, il quale, a sua volta, è omotetico del triangolo ABC perché
hanno i lati a due a due paralleli ( V. § 1.135 punto 3).
Pertanto il triangolo ABC, che è il risultato del prodotto di una isometria, che a DEF fa
corrispondere MNC, e di una omotetia, che ad MNC fa corrispondere ABC, è simile al
triangolo DEF ( V. la definizione di similitudine al § 1.137).
c.v.d.
3.140
Secondo criterio di similitudine dei triangoli
Se due triangoli hanno due lati in proporzione e gli
angoli compresi tra essi congruenti, sono simili
Infatti: dati i triangoli ABC e DEF nei quali è
AC / DF = BC / EF e gli angoli in C ed in F
congruenti, se è pure AC ≅ DF, i due triangoli
sono congruenti per il primo criterio di congruenza
dei triangoli e perciò sono simili.
C
F
M
N
M
A
B
D
E
Se invece si suppone che AC e DF non siano congruenti, ma che, ad es., sia AC > DF,
si procede nel modo descritto nel precedente § e si ottiene di nuovo il triangolo MNC
che è omotetico del triangolo ABC perché i due triangoli hanno gli angoli a due a due
congruenti ( V. § 1.138) e quindi:
AC / MC = BC / NC
Inoltre MNC ≅ DEF per il primo criterio di congruenza dei triangoli. Quindi i triangoli
ABC e DEF sono simili perché corrispondenti nel prodotto di una omotetia e di una
isometria. ( V. la definizione di similitudine al § 1.137)
c.v.d.
3.141
Terzo criterio di similitudine dei triangoli
C
F
Se due triangoli hanno i lati in proporzione sono simili
A
Infatti: dati i due triangoli ABC e DEF che hanno i lati
in proporzione, cioè AB / DE = AC / DF = BC / EF,
se è AC ≅ DF anche AB ≅ DE e BC ≅ EF quindi,
per il terzo criterio di congruenza dei triangoli, i due
triangoli ABC E DEF sono simili.i
M
D
N
E
B
Se si suppone invece che AC e DF non siano congruenti, ma che, ad es. sia AC > DF,
si opera come è stato fatto nei §§ precedenti, ottenendo il triangolo MNC che è omotetico
del triangolo ABC, per le ragioni già esposte prima, e quindi
AC / MC = BC / NC
Inoltre MNC ≅ DEF per il terzo criterio di congruenza dei triangoli.
Quindi i triangoli ABC e DEF sono simili perché corrispondenti nel prodotto di una
omotetia e di una isometria. ( V. la definizione di siilitudine al § 1.137)
c.v.d.
69
3.142
Triangoli simili
Due triangoli sono simili quando esiste una similitudine che trasforma uno
nell’altro. Il che significa che:due triangoli simili hanno gli angoli corrispondenti
congruenti ed i lati corispondenti proporzionali e viceversa
I triangoli simili hanno le seguenti proprietà:
a) Se due triangoli sono simili le altezze, le mediane e le bisettrici, uscenti da vertici
corrispondenti, sono proporzionali a due lati corrispondenti.
Infatti: se due triangoli ABC ed A’B’C’ sono simili, con rapporto di similitudine k, si può
scrivere.
A’B’ / AB = B’C’ / BC = C’A’ / CA = k
Poiché, come è stato detto, rette perpendicolari si trasformano in rette perpendicolari, alla
retta AH, perpendicolare alla retta AB, corrisponde la retta C’H’, perpendicolare alla
retta A’B’. Il punto H’ è quindi corrispondente di H, perché sono intersezioni di rette
corrispondenti.
Di conseguenza le altezze AH ed A’H’ dei due triangoli sono corrispondenti nella
similitudine, cioè A’H’ / AH = k
e quindi
A’H’ / AH = A’B’/ AB
c.v.d.
Analogo ragionamento si può fare per le mediane e le bisettrici che escono da vertici
corrispondenti.
Perciò in due triangoli simili gli ortocentri, i baricentri e gli incentri sono punti
corrispondenti.
b) Il rapporto tra i perimetri di due triangoli simili è uguale al rapporto di
similitudine
Infatti: dati due triangoli ABC e DEF, che per
ipotesi sono simili con rapporto di similitudine k,
risulta: AC / DF = BC / EF = k
Applicando la proprietà del comporre si ha:
(AB + BC + AC) / (DE + EF + DF) = AC / DF
Essendo AC / DF = k anche il rapporto dei
perimetri è uguale a k
c.v.d.
C
F
D
A
E
B
c) Se due triangoli sono simili il rapporto tra le altezze relative a due lati
corrispondenti è uguale al rapporto di similitudine
C
F
Infatti: indicando con CM ed FN le altezze dei
due triangoli simili ABC e DEF, i triangoli
rettangoli AMC e DNF sono simli per il
primo criterio di similitudine.
D N E
Ne consegue che AC / DF = CM / FN e poiché
per ipotesi è AC / DF = k anche CM / FN = k A
M
B
c.v.d.
d) Il rapporto tra le aree di due triangoli simili è uguale al quadrato del rapporto di
similitudine
70
Infatti: se in una similitudine con rapporto k si indicano con b, b’; h, h’; ed S, S’ le
misure delle basi e delle altezze e le aree di due triangoli simili, per il precedente punto a)
si può scrivere:
b’ / b = h’ / h = k
da cui
b’ = k b; h’ = k h
2
2
e quindi
S’ = b’ h’ / 2 = k b h / 2 = k S
ossia
S’ / S = k2
c.v.d.
e) In ogni triangolo rettangolo un cateto è medio proporzionale tra l’ipotenusa e la
proiezione ortogonale di tale cateto sull’ipotenusa
C
Infatti: dato il triangolo rettangolo ABC, con l’angolo retto
in C, essendo per ipotesi
AC perpendicolare a BC,
CH perpendicolare a AB,
si può constatare che i triangoli CAB e CAH sono
simili per il primo criterio di simlitudine.
Si può perciò scrivere AB / AC = AC / AH cioè
A
H
B
2
AB • AH = AC
c.v.d.
f) In ogni triangolo rettangolo l’altezza relativa all’ipotenusa è media proporzionale
tra le proiezioni dei cateti sull’ipotenusa (V. la figura del punto precedente)
Infatti: dato il triangolo rettangolo ABC, con l’angolo retto in C, nel quale:
AC è perpendicolare a BC,
CH è perpendicolare a AB,
risulta che i triangoli ACH e CBH sono simili per il primo criterio di similitudine.
c.v.d.
Si può quindi scrivere: AH / CH = CH / HB cioè AH • HB = CH2
3.143
Criteri di similitudine dei poligoni
Dal § 1.141 si deduce che nei triangoli la congruenza tra due angoli corrispondenti
implica la proporzionalità dei lati pure corrispondenti e viceversa, per cui il
verificarsi di una delle due condizioni consente di stabilire la similitudine tra due
triangoli
Ciò però non è sempre vero per i poligoni. Ad es. un rettangolo ed un quadrato, pur
avendo gli angoli congruenti, non hanno i lati in proporzione, quindi non sono simili.
Similmente un quadrato ed un rombo, pur avendo i lati in proporzione, non hanno gli
angoli congruenti e pertanto non sono simili.
Due poligoni con lo stesso numero di lati sono simili se hanno gli angoli
corrispondenti congruenti ed i lati omologhi in proporzione, ad eccezione di:
a) tre angoli consecutivi oppure:
b) due angoli consecutivi ed il lato compreso tra essi
oppure
c) due lati consecutivi e l’angolo compreso tra essi
Invece due poligoni regolari con lo stesso numero di lati sono simili
Infatti: un poligono regolare è equiangolo per cui ogni angolo di uno è uguale alla
somma degli angoli interni diviso per il numero dei lati.
71
Essendo la somma degli angoli interni di un poligono di n lati: (n – 2) π ( V. § 3.51)
ogni angolo del poligono è uguale a (n – 2) π / n indipendentemente dalla lunghezza dei
lati.
Inoltre il rapporto tra due lati di due poligoni regolari, con lo stesso numero di lati, resta lo
stesso qualunque sia la coppia di lati considerata, perché ognuno dei due poligoni è
equilatero. Allora i lati corrisspondenti sono proporzionali e gli angoli corrispondenti sono
congruenti.
Quindi i due poligoni sono simili.
C.v.d.
3.144
Alcune proprietà dei poligoni simili
(senza dimostrazione)
1) l rapporto tra i perimetri di due poligoni simili è uguale al rapporto di similitudine
( V. il punto b) del precedente §)
2) Il rapporto tra le aree di due poligoni simiii è uguale al quadrato del rapporto di
similitudine ( V. il punto d) del § precedente)
3) Costruendo tutte le diagonali possibili da due vertici corrispondenti di due
poligoni simili, questi vengono divisi nello stesso numero di triangoli
ordinatamente simili
4) Il rapporto tra i perimetri di due poligoni simili, inscritti o circoscritti a due
circonferenze, è uguale al rapporto tra i raggi delle ciconferenze
3.145 La similitudine nelle circonferenze
A) Teorema delle due corde
In una circonferenza due corde incidenti si tagliano in modo che le parti dell’una
rappresentano i medi e le parti dell’altra gli estremi di una proporzione
Infatti: data una circonferenza nella quale sono presenti
due corde AB e CD che si intersecano in un punto P,
se si uniscono A con C e B con D, i triangoli APC e
CPD, da esse formati, sono simili poiché:
APC ≅ BPD essendo opposti al vertice;
ACD ≅ ABD perché sono angoli alla circonferenza che
insistono sullo stesso arco AD
Si ha quindi AP / PC = PD / PB
c.v.d.
C
B
P
A
D
B) Teorema delle due secanti
Se da un punto esterno a una circonferenza si conducono due secanti, un segmento
secante e la sua parte esterna sono i medi e l’altro segmento secante e la sua parte
esterna costituiscono gli estremi di una proporzione
Infatti: data una circonferenza alla quale da un punto P
esterno si conducono due secanti PB e PD, e si uniscono
A con D e C con B, i triangoli PAD e PCB sono simili
72
P
C
per il primo criterio di similitudine, poiché:
l’angolo in P è comune;
ADP ≅ CBP perché angoli alla circonferenza che insistono
sullo stesso arco AC
Quindi si ha: PB / PD = PC / PA
c.v.d.
A
D
B
C) Teorema della secante e della tangente
Se da un punto esterno a una circoferenza si tracciano una tangente ed una
secante, il segmento di tangente è medio proporzionale tra il segmento secante e la
sua parte esterna
P
Infatti: data una circonferenza alla quale da un punto
A
esterno P si conducono la secante PB e la tangente
PC e si uniscono A con C e B con C, i triangoli
PBC e PAC risultano simili per il primo criterio di
B
C
similitudine poiché:
l’angolo in P è comune;
PBC ≅ ACP perché angoli alla circonferenza che insistono sullo stesso arco AC.
Quindi si ha PB / PC = PC / PA
c.v.d.
D) Il raggio della circonferenza circoscritta a un triangolo è dato dal rapporto tra il
prodotto delle misure dei lati del triangolo e il quadruplo della sua area
Infatti: se in una circonferenza di centro O, circoscritta al triangolo ABC, i cui lati sono
AB = a; BC = = b e AC = c, si tracciano l’altezza CH = h, relativa al lato AB del
triangolo, di cui H è il piede e il diametro CD = 2r, i triangoli
ACD e CHB risultano simili perché:
C
CAD ≅ CHB perché sono retti;
ADC ≅ ABC perché angoli alla circonferenza che insistono
O
B
sullo stesso arco AC.
Ne consegue che CD / CB = CA / CH ossia 2 r / b = c / h
H
che si può scrivere 2 r h = b c
da cui
r = b c / 2 h.
A
D
Se si moltiplicano per a numeratore e denominatore della frazione suddetta si ottiene:
r = abc/2ah
che è la formula per calcolare il raggio della circonferenza circoscritta al triangolo
ABC quando ne siano noti i lati.
3.146
Sezione aurea di un segmento
La sezione aurea di un segmento è quella parte del segmento che è media
proporzionale tra l’intero segmento e la rimanente parte
A
C
B
Ad es. dato il segmento AB, il segmento AC ne
è la sezione aurea se è :AB / AC = AC / CB
F
Per costruire la sezione aurea di un dato
segmento si deve:
- tracciare per B la perpendicolare ad AB;
D
O
73
- disegnare la circonferenza di centro O e
E
raggio OB = r congruente alla metà di AB;
r
- tracciare la semiretta AO che interseca la
circonferenza in E e D;
A
C
B
- descrivere con un compasso l’arco di circonferenza di raggio AE che interseca il
segmento AB in C;
La semiretta AD è la secante e AB è la tangente alla circonferenza e quindi, per il punto
C) del precedente §, si ha AD / AB = AB / AE = AB / AC.
Poiché AD ≅ AE + ED si può scrivere ( AE + ED) / AB = AB / AC e siccome, per
costruzione, OB ≅ AB / 2 è ED ≅ AB:
applicando lo scomponendo si ottiene (AE + AB – AB) / AB = (AB – AC) / AC cioè
AE /AB = CB / AC oppure
AC / AB = CB / AC e invertendo si ha:
AB / AC = AC / CB
Il che significa che AC è proprio la sezione aurea del segmento AB.
C.v.d.
4
4.1
GEOMETRIA NELLO SPAZIO
Premessa
Mentre nella geometria nel piano si sono studiate le figure piane, nella geometria nello
spazio o stereometria si studiano le figure geometriche solide.
74
I punti, le rette e i piani sono gli elementi fondamentali dello spazio.
Tutti gli assiomi considerati nella geometria del piano hanno piena validità anche nella
geometria solida.
4.2
LO SPAZIO
Mentre nella geometria piana si era considerato un solo piano, nella geometria solida si
considerano infiniti piani disposti nello spazio.
Per individuarli e distinguerli si usa comunemente indicarli con le prime lettere dell’alfabeto
greco: α (alfa); β (beta); γ (gamma); ecc.
4.3 I semispazi
Nella geometria piana si era visto che una retta su un piano lo divide in due semipiani,
Nella geometria solida un piano divide lo spazio in due semispazi, che si dicono
opposti l’uno all’altro.
Tale piano si chiama contorno o frontiera o origine dei semispazi
I punti di un semispazio, non appartenenti al contorno, si dicono interni al
semispazio.
Due punti appartenenti a semispazi opposti si dicono situati da parti o bande
opposte rispetto al contorno.
Sono intuitive le seguenti proprietà relative ai semispazi.
a) Una semiretta che congiunge un punto A del contorno
di un semispazio con un punto B interno ad esso,
appartiene completamente a quel semispazio.
A
B
M
b) Un segmento MN che congiunge due punti interni di
un semispazio appartiene completamenmte allo stesso
N.
P
c) Un segmento che congiunge due punti P e Q, situati
in semispazi opposti, appartiene in parte ad un
semispazio ed in parte a quello opposto,
ed attraversa la frontiera in un punto R.
4.4
R
Q
α
Piani nello spazio
P
E’ evidente che:
Per un punto P nello spazio passano infiniti
piani che formano una figura geometrica chiamata stella di piani di cui il punto P è
il sostegno
E’ pure evidente che:
Per due punti A e B, nello spazio, passano Infiniti
piani e quindi ne passano anche infiniti per la retta r
75
B
cui appartengono i due punti.
A
Se si prende un terzo punto C non appartenente alla
retta AB, si verifica facilmente che:
Per tre punti non allieati nello spazio passa un
piano ed uno solo.
C
r
Conseguentemente:
Due piani distinti nello spazio non possono avere in comune tre punti non allineati.
E si può anche dire che
Una retta ed un punto esterno ad essa individuano un piano ed uno solo.
Se si considerano due rette r ed s, che si intersecano
in un punto P e si prendono un punto A su r ed un
punto B su s, non coincidenti con P, il piano che
passa per A, B e C contiene entrambe le rette.
r
Si può quindi affermare:
Due rette incidenti determinano un piano ed
uno solo.
s
α
A
P
B
Analogamente al fascio (proprio) di rette definito nella geometria piana, l’insieme di infiniti
piani che passano per una retta formano un fascio (proprio) di piani di cui la retta r è il
sostegno.
4.5
Posizioni reciproche di due piani nello spazio
Si è visto prima che due piani distinti nello spazio non possono avere in comune tre punti
non allineati.
r
I casi che invece si possono verificare sono i seguenti:
α
1° caso)
I due piani hanno due punti in comune
A
β
In questo caso se A e B sono i due punti in comune
a due piani α e β, la retta r che passa per essi giace
su entrambi i piani, e si può quindi affermare:
Se due piani hanno in comune due punti allora essi
hanno in comune anche la retta a cui i due punti
appartengono.
β
B
In questo caso i due piani si dicono incidenti e la retta è detta intersezione dei due
piani.
2° caso)
I due piani hanno in comune un solo punto
In tale caso se si considera un piano α ( ad es. la
plancia di un tavolo) su cui appoggia in un solo punto
A un semipiano β, se si prende in esame tutto il piano
di cui β fa parte, si constata che tale piano attraversa
76
α
β
A
B
o sega il piano α secondo una retta che, ovviamente,
appartiene ad α ed a β.
Si può perciò affermare:
Due piani aventi un punto in comune si segano
secondo una retta che passa per tale punto.
3° caso)
I due piani non hanno alcun punto in comune
E’ evidente che possono esserci dei piani che non hanno punti in comune.
In tale caso essi si dicono paralleli.
4.6
Posizioni reciproche di due rette nello spazio
Secondo la geometria nel piano per due punti passa una ed una sola retta, per cui due
rette distinte non possono avere in comune due punti.
Questo assioma è valido anche per la geometria nello spazio.
I casi che, invece, si possono verificare nello spazio sono i seguenti:
1° caso)
Le due rette giacciono sullo stesso piano
ed hanno un solo punto in comune
In tale caso le rette r ed s, che si intersecano nel
punto P, sono dette incidenti
2° caso)
α
P
r
Le due rette giacciono sullo stesso piano ma non hanno punti in comune
In questo caso le rette a e b, che stanno sul piano
β, ma non hanno alcun punto in comune, sono dette
parallele
3° caso)
s
r
s
β
Le due rette non giacciono nello stesso piano e non hanno quindi alcun
punto in comune
In questo caso le rette si dicono sghembe
a
Nel 1° e nel 2° caso le rette si dicono complanari
4.7
b
Posizioni reciproche di una retta e un piano nello spazio
Nello spazio una retta ed un piano possono avere le seguenti posizioni reciproche:
1°) La retta appartiene al piano
Nella geometria piana una retta che ha due punti A e B
in comune con un piano α, giace completamente sul piano.
Questo postulato è valido anche nella geometria solida.
2°)
La retta è incidente a un piano
77
B
A
α
r
P
Una retta r che ha in comune con un piano β un solo
punto P è detta incidente al piano.
3°)
La retta è parallela ad un piano
β
r
γ
Una retta r che non ha alcun punto in comune con
un piano γ si dice parallela al piano.
4.8
Rette e piani perpendicolari
r
H
Se una retta r è perpendicolare a due rette a e b
che individuano un piano β e che si intersecano in
uno dei suoi punti P, è pure perpendicolare a
qualunque altra retta passante per P.
β
P
Infatti: presi sulle rette a e b due punti, A e B,
A
C
B
in modo che sia PA ≅ PB, e sulla retta r pure
a
c
b
due punti H e K tali che sia PH ≅ PK, si uniscono
tra loro A e B indicando con C l’intersezione della
retta AB con una qualunque retta, come la c, passante
K
per P e giacente sul piano β.
I triangoli APH e APK sono congruenti perché sono
rettangoli in P per ipotesi, hanno in comune il cateto AP ed i cateti PH e PK congruenti
per costruzione. Quindi risulta AH ≅ AK.
Parimenti, considerando i triangoli BPH e BPK si dimostra che BH ≅ BK.
Inoltre anche i triangoli APH e BPH sono congruenti perché rettangoli in P per ipotesi,
hanno il cateto PH in comune ed i cateti PA e PB congruenti per costruzione.
Quindi AH ≅ BH.
Ne consegue che il triangolo ABH è isoscele e così pure il triangolo ABK e questi due
triangoli sono tra loro congruenti per il terzo criterio di congruenza.
Quindi anche i triangoli ACH e ACK sono congruenti avendo il lato AC in comune,
AH ≅ AK e CAH ≅ CAK per quanto dimostrato.in precedenza.
Risulta perciò CH ≅ CK. I triangoli CPH e CPK sono allora congruenti per il terzo
criterio di congruenza e pertanto CPH ≅ CPK perché, essendo tra loro supplementari,
sono retti.
Quindi la retta r è perpendicolare ad ogni retta c passante per P e giacente sul piano
β.
C.v.d.
La retta r si chiama perpendicolare al piano β.
perpendicolare.
Il suo punto P è il piede della
Riguardo alla perpendicolarità sono valide le seguenti proprietà
1) Per ogni punto dello spazio passa una ed una sola perpendicolare ad un dato
piano
a
b
Di conseguenza:
78
2) Due rette a e b perpendicolari allo stesso
piano α sono tra loro parallele
4.9
α
Distanza di un punto da un piano
P
Dato un piano β ed un punto P , esterno ad esso,
dal quale viene condotta la perpendicolare a β,
della quale H è il piede, è intuitivo che il segmento
PH è minore di qualunque altro segmento, come
ad es. PA o PB. che congiunge P con dei punti,
come A o B, appartenenti allo stesso piano β.
Il segmento PH, cioè il segmento di perpendicolare
condotta da P al piano β, è detto distanza da
quel punto al piano.
β
A
H
B
A
4.10
Distanze di rette e piani
B
A
r
Dato un piano α ed una retta r,
se si prendono sulla r due punti
A’
r
A’
B’
A e B, le loro distanze AA’ e
α
B’
α
BB’ dal piano α sono differenti
se la retta r è incidente al piano
mentre sono congruenti se la r è parallela al piano.
Si può quindi affermare:
Data una retta parallela ad un piano, si chiama distanza della retta dal piano il
segmento di perpendicolare condotta da un punto qualsiasi della retta al piano.
Si può pure facilmente constatare che, dati due piani
α e β, tra loro paralleli, tutti i punti di un piano hanno
la medesima distanza (AA’ ≅ BB’) dall’altro piano
Si può quindi affermare:
Si chiama distanza tra due piani paralleli il segmento
di perpendicolare condotta da un punto qualunque
di un piano all’altro.
4.11
A
B
A’
B’
≅
β
Diedri
Dati due semipiani, α e β, aventi entrambi come frontiera la retta r, essi dividono tuttto
lo spazio in due parti, ognuna delle quali si chiama diedro.
Cioè:
Si chiama diedro ognuna delle due parti in cui lo spazio
è diviso da due semipiani aventi la stessa frontiera.
β
Per analogia con l’angolo della geometria piana, il diedro
si può anche chiamare angolo diedro.
I due semipiani si dicono facce del diedro; esse
costituiscono la superficie o il contorno del diedro;
79
α
r
la retta che è la frontiera dei due semipiani si chiama
costola o spigolo del diedro.
I punti del diedro che non appartengono al contorno si dicono interni
Un diedro che ha per facce i semipiani α e β si indica con il simbolo αβ,
oppure ArB, se A e B sono due punti, uno su una faccia, l’altro sull’altra ed r è lo
spigolo del diedro.
Due diedri si dicono congruenti quando con un movimento rigido si possono sovrapporre
esattamente l’uno sull’altro.
4.12
Piani perpendicolari
Due piani α e β, che si intersecano,
formano quattro angoli diedri che,
come gli angoli opposti al vertice nella
geometria piana, sono congruenti a
due a due.
Se i quattro diedri sono tutti congruenti
tra loro, i due piani sono perpendicolari.
Per cui:
due piani che si intersecano, se formano
quattro angoli diedri congruenti, si dicono
perpendicolari.
4.13
β
D’
PRISMI
C’
Si chiama prisma un solido limitato da due
poligoni congruenti, giacenti su due piani
paralleli α e β, e da tanti parallelogrammi
quanti sono i lati dei due poligoni
E’
H’
B’
A’
α
D
E.
I due poligoni si chiamano basi del prisma
I parallelogrammi sono le facce laterali
.
La distanza tra i piani su cui giacciono le
E
B
basi è l’altezza del prisma.
H
A
I lati che limitano le basi, cioè i lati dei poligoni,
si chiamano spigoli di base, quelli che limitano le facce sono gli spigoli laterali.
Gli spigoli laterali sono congruenti perché sono a due a due i lati opposti di un
parallelogrammo.
L’insieme di tutte le facce costituisce la superficie laterale; l’insieme delle due basi e
della superficie laterale è la superficie totale del prisma.
A seconda dei poligoni che costituiscono le basi. triangoli, quadrangoli, pentagoni, ecc
un prisma si chiama triangolare, quadrangolare, pentagonale, ecc.
Il prisma in figura è pentagonale; i pentagoni: ABCDE e A’B’C’D’E’ sono le basi; i
segmenti: AB, BC, CD, DE, EA sono gli spigoli di base; i segmenti: AA’, BB’, CC’; DD’,
EE’; sono gli spigoli laterali; il segmento HH’ è l’altezza del prisma.
80
4.14
Prisma retto e prisma regolare
Un prisma si dice retto quando gli spigoli
laterali sono perpendicolari ai piani delle
basi
Un prisma retto ha come facce laterali dei
rettangoli e l’altezza è congruente con gli
spigoli laterali
Un prisma non retto è detto obliquo
Quando le basi di un prisma retto sono dei
poligoni regolari il prisma si dice regolare.
( Iin figra un prisma quadrangolare e triangolare, regolari )
4.15 Area della superficie di un prisma retto
Se si immagina di tagliare un prisma retto lungo
tutti gli spigoli, tranne uno, di entrambe le basi
e lungo un solo spigolo laterale e poi di aprirlo,
si ottiene lo sviluppo della superficie totale del
prisma su un piano, come l’immagine della
figura qui a fianco, che rappresenta lo sviluppo
di un prisma quadrangolare.
Lo
sviluppo è costituito dai due poligoni di
base e dalla superficie laterale del prisma che
è un rettangolo con la base congruente al
perimetro p del prisma e l’altezza h
congruente con quella del prisma.
Di conseguenza si può affermare che:
L’area della superficie laterale di un prisma
retto è data dal prodotto della misura del perimetro del poligono di base per la
misura dell’altezza e quindi la formula è
Al = p h
L’area della superficie totale si ottiene aggiungendo all’area della superficie laterale
Al la somma delle aree delle due basi 2Ab.
At = Al + 2Ab
Si può quindi dire che:
L’area della superficie totale di un prisma retto è data dalla somma dell’area della
superficie laterale e delle aree delle due basi.
4.16 Parallelepipedo
Un parallelepipedo è un prisma le cui basi sono
dei parallelogrammiIn un parallelepipedo due facce che non hanno alcun
spigolo in comune si dicono opposte; due vertici si
dicono opposti quando non appartengono alla stessa
81
faccia.
Ovviamente le due facce opposte di un parallelepipedo
sono congruenti e giacciono su piani paralleli.
I segmenti che in un parallelepipedo congiungono due vertici opposti si
chiamano diagonali del parallelepipedo.
Le diagonali di un parallelepipedo sono quattro e passano tutte per lo stesso punto
che è il punto medio di ognuna di loro. Un parallelepipedo che ha gli spigoli laterali
perpendicolari ai piani delle basi si dice retto; in caso contrario viene detto obliquo.
Le basi del parallelepipedo retto sono dei rettangoli
4.17 Parallelepipedo rettangolo
Un parallelepipedo retto che ha pure due rettangoli come basi viene chiamato
parallelepipedo rettangolo.
In questo caso tutte le facce sono dei rettangolii e
Sonio a due a due congruenti: tutti gli spigoli
che hanno origine nello stesso vertice
rappresentano le tre dimensioni del parallelepipedo
retto: esse sono la lunghezza a, la larghezza b
e l’altezza c.
c
4.18 Area della superficie di un parallelepipedo rettangolo
Naturalmente per calcolare l’ area della superficie totale di un parallelepipedo rettangolo
si possono usare le formule ricavate nel § 4.15.
Però si può anche semplicemente osservare che, essendo le facce del parallelepipedo
rettangolo a due a due congruenti, basta calcolare le aree di tre facce diverse, a b, b c,
e c a, e poi sommare questi tre prodotti e moltiplicare il risultato della somma per 2.
La formula semplificata per calcolare l’area totale di un parallelepipedo rettangolo
è quindi
At = 2 ( a b + b c + ca )
4.19
Misura della diagonale di un parallelepipedo rettangolo
In un parallelepipedo rettangolo le quattro diagonali sono tutte tra loro congruenti.
Se le sue tre dimensioni a, b, c, sono note,
per ricavare la misura di una diagonale d,
come ad es, BD’, si deve prima calcolare,
D’
mediante il teorema di Pitagora, la misura
A’
C’
della diagonale della base BD che è:
B’ ’
db = √ a2 + b2
e poi calcolare la misura della diagonale
D
c
BD’ = d, che quella voluta, mediante la
A
C
formula:
a
b
82
d = √ a2 + b2 + c2
B
La regola per il calcolo della diagonale di un parallelepipedo rettangolo è quindi:
In un parallelepipedo rettangolo la misura della diagonale si calcola estraendo la
radice quadrata della somma dei quadrati delle sue tre dimensioni.
4.20 Cubo
Il cubo è un parallelepipedo rettangolo che ha le tre
dimensioni congruenti e quindi le sue 6 facce sono
dei quadrati.
Se l è la misura del lato di uno dei 6 quadrati, la formula
per il calcolo della superficie totale di un cubo è:
At = 6 • l 2
La formula per il calcolo della diagonale di un cubo,
ricavata dalla formula del § precedente, è data da
d = √3 • l
4.21 PIRAMIDI
Si chiama piramide un solido limitato da un poligono e da tanti triangoli quanti sono
i lati del poligono, aventi tutti un vertice comune non appartenente al piano del
poligono.
Il poligono è la base.
I triangoli sono le facce laterali.
Il vertice comune dei triangoli è il vertice
della piramide.
Gli spigoli che coincidono con i lati della
base sono gli spigoli di base; gli altri :
gli spigoli laterali.
La distanza del vertice dalla base della
piramide ne è l’altezza.
La superficie laterale di una piramide
è l ’insieme delle facce laterali.
La somma della superficie laterale e della base dà la superficie totale.
Nella figura il quadrangolo ABCD è la base, il punto V è il vertice; i segmenti AB, BC,
CD, DA sono gli spigoli di base, i segmenti VA, VB,VC, VD sono gli spigoli laterali, il
segmento VH è l’altezza
La piramide prende il nome dal tipo di poligono di base: dal triangolo. dal quadrangolo, dal
pentagono, ecc la piramide viene detta: triangolare, quadrangolare, pentagonale, ecc
4.22
Piramide retta
83
Se nel poligono di base di una piramide è inscrittibile una circonferenza e se il piede della
sua altezza coincide con il centro O della circonferenza
V
inscritta, la piramide è retta.
Si può quindi dire:
una piramide è retta quando nella base si può inscrivere
una circonferenza il cui centro è il piede dell’altezza (VO)
Una piramide retta gode delle seguenti proprietà:
1) le facce laterali (triangolari) hanno tutte la stessa
altezza, chiamata apotema della piramide (VH)
2) i piedi delle apoteme sono i punti in cui gli spigoli dt
base sono tangenti alla circonferenza inscritta nella
base
4,23
E
D
A
O
C
B
Piramide regolare
V
Una piramide che ha per base un poligono regolare
si dice regolare
In questo caso le facce laterali sono dei triangoli
Isosceli tutti tra loro congruenti
Poiché in un triangolo isoscele l’altezza coincide con
F
E
la mediana, si può dire:
L’apotema (come VH ) di una piramide regolare è
A
O
il segmento che unisce il vertice con il punto medio
di uno spigolo di base ( CD )
B
C
Inoltre, poiché il triangolo VOH è rettangolo, se sono noti
V
due dei suoi lati si può calcolare il terzo mediante il teorema di Pitagora
4.24
D
a
Area della superficie laterale e totale di una
piramide retta
l3
D
l4
O
C
H l2
Data una piramide retta, ad es quadrangolare, i cui lati sono
l1, l2, l3, l4 e l’apotema a, si può calcolare la superficie laterale
A
l1
B
sommando le aree delle facce laterali, che sono: l1• a /2 ; l2• a /2 ; l3• a /2 ; l4• a/2
Indicando quindi con Al la superficie laterale della piramide, la formula per calcolarla è
Al = a/2 ( l1 + l2 + l3 + l4 )
Ma, poiché la somma tra parentesi è il perimetro p del poligono di base, la formula
precedente può essere scritta, in modo più semplice
Al = a p /2
Cioè : l’area della superficie laterale di una piramide retta è data dal prodotto della
misura del perimetro di base per la misura dell’apotema.
Da tale formula si possono calcolare:
p = 2 Al / a
e
84
a = 2 Al / p
L’area della superficie totale di una piramide retta si ottiene aggiungendo all’area
della superficie laterale quella dell’area della base e quindi la formula è:
At = Al + Ab
4.25
Tronco di piramide
Se si taglia ad una certa altezza una piramide con un piano parallelo a quello della base, il
solido compreso tra i due piani è un tronco di piramide.
In altre parole:
Il tronco di piramide è limitato da due
poligoni, posti su piani paralleli, che
sono le basi del tronco e lateralmente
da tanti trapezi, quanti sono i lati del
poligono, che formano la superficie
laterale del tronco di piramide
La superficie laterale, sommata alle
superfici delle basi, formano la superficie
totale.
La distanza tra i due piani su cui giacciono
le basi è l’altezza del tronco di piramide.
4.26
Tronco di piramide regolare
Un tronco di piramide ottenuto da una piramide retta
si dice retto; se è ottenuto da una piramide regolare
si chiama regolare.
l’
a
Un tronco di piramide regolare ha come basi dei
poligoni regolari e come facce laterali dei trapezi
tutti tra loro congruenti e con la stessa altezza
detta apotema del tronco di piramide
l
L’area della superficie laterale del tronco di piramide è data dalla somma delle aree dei
suddetti trapezi. Quindi se l è la misura del lato di una base , l’ la misura del lato
dell’altra base ed a l’apotema, l’area Af di una delle facce laterali, è
Af = (l + l’) a / 2
E quindi , se n sono i lati dei poligoni di base, l’area della superficie laterale del tronco
di piramide è data dalla formula:
Al = n Af = (n a /2)( l + l’ )
Ma essendo n l ed n l’ i perimetri, rispettivamente, p e p’ della due basi,
si può, più semplicemente, scrivere:
Al = ( p + p’ ) a / 2
E si può quindi dire che:
l’area della supeficie laterale del tronco di piramide regolare è dato dal prodotto
della semisomma delle misure dei perimetri delle basi per la misura dell’apotema.
85
Indicando con At l’area della superficie totale e con A ed A’ l’area delle due basi si ha:
L’area della superficie totale del tronco di piramide si ottiene sommando all’area
della superficie laterale quella delle due basi e la formula è quindi::
At = Al + A + A’
4.27
POLIEDRI
Si chiama poliedro qualunque solido limitato da un numero finito di poligoni situati
in piani diversi e disposti in modo che ognuno dei lati sia comune a due di essi e
che il piano di ciascuno lasci tutti gli altri da una stessa parte.
I poligoni sono le facce; i vertici, i lati e gli angoli sono i vertici, gli spigoli e gli angoli del
poliedro.
In ogni spigolo c’è un diedro che si chiama diedro del poligono.
La somma delle aree di tutte le facce costituisce la superfice poliedrica
Il numero minimo delle facce dI un poliedro è quattro.
Il nome dei poliedri deriva dal numero delle facce: se sono 4 si chiama tetraedro; 5 :
pentaedro; 6: esaedro; 7: ettaedro; 8: ottaedro; 12: dodecaedro; 20: icosaedro; ecc
I poliedri godono di una importante proprietà che ha il nome di:
Relazione di Eulero:
Tra il numero F delle facce, quello V dei vettici e quello S degli spigoli di un
qualsiasi poliedro vale la relazione
F+V = S+2
Ad es un ottaedro ha 6 facce, 8 vertici e 12 spigoli: 6 + 8 = 14 = 12 + 2
4.28
Poliedri regolari
Un poliedro viene detto regolare se ha per facce dei poligoni regolari tutti tra loro
congruenti e pure congruenti i diedri formati da due facce consecutive.
I poligoni regolari sono solo cinque e sono detti solidi platonici. Eccoli
1°) Tetraedro regolare
E’ un poliedro limitato da 4 facce costituite da triangoli equilateri tutti tra loro congruenti,
ha 6 spigoli e 4 vertici.
E’ praticamente una piramide
regolare a base triangolare
Nella figura è rappresentato
un tetraedro ed il suo sviluppo
che è un triangolo equilatero
con il lato uguale al doppio
dello spigolo del tetraedro.
86
2°) Esaedro regolare
E’ un poliedro limitato
da 6 facce che sono
dei quadrati, tutti tra
loro congruenti; ha
8 spigoli e 8 vertici
E’ un cubo, che è
rappresentato In
figura con il suo
sviluppo.
3°) Ottaedro regolare
E’ un poliedro limitato da 8 triangoli equilateri congruenti tra loro, ha 6 vertici e 12
spigoli.
Si può considerare come
l’unione di due piramidi
quadrangolari regolari,
con la base in comune,
situate da parti opposte
rispetto ad essa.
4°) Dodecaedro regolare
E’ un poliedro limitato da 12 pentagoni regolari tutti congruenti tra loro, ha 20 vertici e 30
spigoli.
5°) Icosadro regolare
E’ un poliedro limitato da 20 triangoli tutti tra loro congruenti, ha 12 vertici e 30 spigoli.
4.29
Solidi equivalenti
Si è visto in geometria piana che le figure hanno delle superfici dotate di una certa
estensione chiamata area.
Si è pure visto che più figure piane possono avere uguale estensione ed uguale forma,
oppure estensione uguale ma forma diversa. Si era pure detto che figure piane con la
stessa estensione si definiscono equivalenti.
Anche nella geometria solida si possono avere
figure solide con la stessa estensione e forme
uguali o differenti.
Nella figura sono rappresentati due cubi con la
stessa forma e la stessa estensione
87
Se però si immagina di suddividere
i due cubi,.ciascuno in otto
cubetti tutti congruenti tra
loro, si può osservare che
tali cubetti possono essere
disposti in modo differente:
uno ancora a forma di cubo
e l’altro a forma parallelepipedo,
avendo ovviamente le stesse estensioni, pur con forme diverse, come si vede nella
seconda figura.
In questo caso, in analogia con le figure piane, si dà la seguente definizione:
Due solidi che hanno la stessa estensione si dicono equivalenti.
4.30
VOLUME DEI SOLIDI
Come nella geometria piana si possono misurare le estensioni delle figure piane. cioè le
aree, così pure nella geometria solida si possono misurare le estensioni dei solidi , ma per
compiere questa operazione occorre stabilire una unità di misura dei solidi.
Come unità di misura dei solidi è stato scelto il metro cubo, cioè un cubo avente lo
spigolo lungo 1 metro, il cui simbolo è m3.
I multipli del m3 sono:
Decametro cubo =
Ettometro cubo =
Chilometro cubo =
Miriametro cubo =
1 000 m3
1 000 000 m3
1 000 000 000 m3
1 000 000 000 000 m3
I sottomultipli del m3 sono:
Decimetro cubo = 1 millesimo di m3
Centimetro cubo = 1 milionesimo di m3
Millimetro cubo = 1 miliardesimo di m3
La misura dell’estensione di un solido è quel numero che indica quante volte l’unità
di misura contiene o è contenuta nel solido dato e prende il nome di volume del
solido
Ad es. se in un contenitore stanno esattamente 24 scatole a forma di cubo, di 2500 cm3
ciascuna, si dirà che il volume di quel contenitore è di 24 • 2.500 = 60. 000 cm3 =
60 cm3 = 0,06 m3
E’ evidente, per quanto detto prima. che solidi equivalenti hanno lo stesso volume e
viceversa.
4.31
Volume del parallelepipedo rettangolo
88
Conoscendo le tre dimensioni di un parallelepipedo rettangolo a, b c, analogamente a
quanto si è fatto per calcolare l’area di un rettangolo, per calcolare il volume del
parallelepipedo rettangolo si deve moltiplicare a per b e il risultato per c. Per cui:
Il volume di un parallelepipedo rettangolo è uguale al prodotto delle sue tre
dimensioni e la formula è quindi:
V = abc
Poiché il prodotto a b è l’area Ab di una faccia che si può considerare base del solido,
per cui c ne è l’altezza h, la regola precedente può diventare la seguente:
Il volume di un parallelepipedo rettangolo è uguale al prodotto dell’area di base per
la relativa altezza, e la formula diventa:
V = Ab h
da cui si possono ricavare:
Ab = V / h
e
h = V / Ab
4.32
Volume del cubo
Poiché il cubo non è altro che un parallelepipedo con le tre dimensioni uguali, la regola per
il calcolo del volume del cubo è:
Il volume di un cubo è uguale alla misura dello spigolo elevata alla terza potenza, e
la formula è quindi:
V = l3
da cui si può ricavare
l = 3√ V
ciioè: la misura dello spigolo di un cubo si ottiene estraendo la radice cubica del suo
volume
4.33
Volume del prisma
Si può dimostrare che un prisma
ed un parallelepipedo rettangolo
aventi altezze congruenti e basi
equivalenti sono pure tra loro
equivalenti.
Avendo visto nel § 4.31 che il
volume del parallelepipedo
rettangolo si ottiene moltiplicando
l’area della base per la misura della relativa altezza, si può dire:
Il volume di un prisma è uguale al prodotto dell’area di una sua base Ab per la
misura della relativa altezza h e la formula è quindi:
V = Ab h
da cui si possono ricavare:
Ab = V / h
e
h = V / Ab
4.34
Volume della piramide
89
Data una piramide ed un prisma aventi
base ed altezza congruenti si può
dimostrare che la piramide è equivalente
ad un terzo del prisma, per cui si può dire,
ricordando che il volume del prisma si
calcola moltiplicando l’area della base
per la misura della relativa altezza:
Il volume di una piramide si ottiene
moltiplicando l’area della base per la misura dell’altezza e dividendo il loro
prodotto per 3 e la formula è quindi:
V = Ab h / 3
da cui si possono ricavare
Ab = 3 V / h
e
h = 3 V / Ab
4.35
Volume del tronco di piramide
Il tronco di piramide può essere considerato, come si
h1 hè
visto al § 4.26, una piramide alla quale è stata
tagliata, con un piano parallelo alla base, la parte
A1
superiore, che è pure una piramide avente come
base la base superiore, piccola, del tronco e
h
come altezza la differenza tra l’altezza della
piramide completa e l’altezza del tronco.
A
Ciò premesso, se si indicano:
con A ed A1 le due basi, maggiore e minore,
del tronco, con h l’altezza del tronco e con
h1 l’altezza della piccola piramide, con VT il volume del tronco, con V il volume della
piramide grande e con V1 il volume della piramide piccola, si può scrivere:
V1 = A1 h1 / 3
VT = V – V1
V = A ( h + h1) / 3
VT = (A h + A h1 – A1 h1) / 3 =
A h + (A – A1) h1 / 3
(1)
Ricor hdando il punto 2) del § 3.144- 2) relativo al rapporto di similitudine dei poligoni,
si può scrivere:
A / A1 = (h + h1)2 / h12
da cui si ha
A h12 = A1 ( h2 + h12 + 2 h h1 )
e, ordinando e semplificando, si ottiene un’equazione di 2° grado nell’incognita h 1
( A – A1 ) h12 – 2 A1 h h1 – A1 h2 = 0
che, risolta, dà
h1 = A1 h ± √ A12 h2 + A1 h2 ( A – A1 ) / ( A – A1 ) = ( A1 h ± h √ A A1 ) / ( A – A1 )
Sostituendo nella (1) il valore di h1 trovato si ottiene:
VT = ( A h + A1 h + h √ A A1 ) / 3 = (A + A1 + √ A A1 ) h / 3
che è la formula per il calcolo del volume del tronco di piramide.
4.36
SOLIDI DI ROTAZIONE
90
I solidi di rotazione sono delle figure solide generate dalla rotazione completa di una
figura piana attorno ad uno dei suoi lati.
4.37
Il cilindro
Si chiama cilindro un solido ottenuto facendo compiere una rotazione completa di
un rettangolo attorno ad un lato ( ad es. AD ) che si chiama asse del cilindro.
I due cerchi, tra loro congruenti, situati su
piani paralleli, descritti dai lati AB e CD
durante la rotazione, sono le basi del
D
C
cilindro ed i lati suddetti ne sono i raggi.
La superficie descritta dal lato BC, è la
superficie laterale del cilindro.
La somma della superficie laterale e di
quella delle due basi è la superficie totale.
Il lato BC è detto generatrice del cilindro
A
B
che è congruente alla generatrice ed all’asse
Un cilindro che ha il diametro delle basi congruente all’altezza è detto equilatero.
4.38
Area della superficie di un cilindro
Se si immagina di tagliare un cilindro
lungo una generatrice e lungo le
circonferenze delle basi, tranne un
punto per ogni base, e si distende la
superficie così ottenuta su un piano
si ottiene lo sviluppo della superficie
Superficie laterale
totale del cilindro, che è composta
dai due cerchi delle basi e da un
rettangolo che ha per base la
circonferenza rettificata del cilindro
e per altezza quella del cilindro.
La figura rappresenta lo sviluppo
totale del cilindro raffigurato nel § precedente.
Il rettangolo è la superficie laterale. Indicando con r la misura
del raggio delle basi e con h l’altezza del cilindro e con Al
l’area della superficie laterale si può dire
Base
Base
L’area della superficie laterale di un cilindro si ottiene moltiplicando la misura della
circonferenza di una base per la misura dell’altezza del cilindro e quindi la formula è:
Al = 2 π r h
da cui si possono ricavare:
r = Al / 2 π h
e
h = Al / 2 π r
L’area della superficie totale si ottiene sommando all’area della superficie laterale
quella delle due basi ed è quindi espressa dalla formula:
At = 2 π r h + 2 π r2 = 2 π r (h + r)
91
4,39
Volume del cilindro
Si può dimostrare che un cilindro ed un prisma
aventi la stessa altezza e le basi equivalenti,
sono equivalenti e hanno perciò lo stesso volume.
Si può quindi dire:
Il volume di un cilindro si ottiene moltiplicando
l’area del cerchio di base per la misura
dell’altezza e quindi la formula è
V = π r2 h
da cui si ricavano
h = V / π r2
e
r = √V/πh
4.40 Il cono
h
C
Il cono si ottiene facendo compiere una
rotazione completa di un triangolo rettangolo
attorno ad un cateto, ad es. AC, detto asse
del cono.
Il cerchio descritto nella rotazione dall’altro
A
B
cateto, AB, è la base del cono, di cui tale
cateto è il raggio.
L’ipotenusa del triangolo rettangolo genera
durante la rotazione una superficie curva detta superficie conica, che è la superficie
laterale del cono.
La superficie totale del cono si ottiene sommando alla superficie laterale la superficie
della base.
L’ipotenusa viene detta generatrice o apotema del cono.
Il vertice del triangolo si chiama vertice del cono.
Il cateto-asse del cono è l’altezza del cono
Un cono che ha il diametro della base congruente all’altezza è detto equilatero
4.41
Area della superficie del cono
Se si immagina di tagliare la superficie laterale di un cono lungo una generatrice, dopo
aver staccato la base, e di distenderla su un piano, si ottiene una figura piana detta
sviluppo della superficie laterale del cono,
che consiste in un settore circolare avente
come raggio l’apotema del cono e la
a
lunghezza del suo arco congruente a
quella della circonferenza della base
del cono.
Qui a fianco è rappresentato lo sviluppo della
superficie laterale del cono della figura del
§ precedente in cui r è il raggio della base
ed a l’apotema del cono.
92
2πr
Detta quindi a la misura dell’apotema del cono ed r la misura del raggio della base,
ricordando quanto detto al § 3.133 in merito al calcolo dell’area di un settore circolare, si
può scrivere:
l’area della superficie laterale Al di un cono è la metà del prodotto della misura
della circonferenza di base per la misura dell’apotema per cui la formula è:
Al = 2 π r a / 2 = π r a
da cui si possono ricavare:
e
a = Al / π r
r = Al / π a
L’area della superficie totale At si ottiene sommando all’area della superficie
laterale quella della base Ab e la formula è quindi:
At = Al + Ab = π r a + π r2 = π r (a + r)
4.42
Volume del cono
Si può dimostrare che un cono è equivalente ad una piramide avente la stessa altezza e
come base un poligono equivalente al cerchio di base del cono. Per cui, come per la
piramide:,
il volume del cono si ottiene moltiplicando l’area della base per l’altezza h e
dividendo il prodotto per 3, e quindi la formula è:
V = π r2 h / 3
da cui si possono ricavare:
h = 3 V / π r2
e
r = √3V/πh
4.43
Il tronco di cono
Come per la piramide, il tronco di cono si ottiene tagliando con un piano parallelo alla base
la parte superiore di un cono.
Poiché però nel disegno qui a fianco si nota che la
figura OABO’ è un trapezio rettangolo, si può
anche dire che:
O’
B
h
Un tronco di cono si può ottenere facendo compiere
una rotazione completa di un trapezio attorno al lato
OO’ .
O
A
Il tronco di cono ha due cerchi, di centro O ed O’,
come basi e la distanza h tra le due basi è
l’altezza del tronco di cono.
Il segmento di una generatrice del cono, compreso tra le due basi si chiama generatrice o
apotema del tronco di cono.
La parte di superficie conica compresa tra le due basi è la superficie laterale del tronco
di cono.
La superficie totale si ottiene sommando alla supertìficie laterale quella delle due basi..
4.44
Area della superficie e volume del tronco di cono
Il calcolo per ricavare l’area della superficie laterale del tronco di cono è analogo a quello
effettuato al § 4.26 per il tronco di piramide, per cui si può scrivere:l’area della
superficie laterale del tronco di cono Al si ottiene moltiplicando la semisomma
93
delle lunghezze delle circonferenze delle basi, di raggio r ed r’, per la misura
dell’apotema del tronco e quindi la formula è:
Al = (2 π r + 2 π r’) a / 2 = π (r + r’) a
da cui si possono ricavare:
a = Al / π (r + r’)
e
r + r’ = Al / π a
L’area della superficie totale At , indicando con A = π r2 e con A’ = π r’2, le superfici
delle due basi, è quindi
At = Al + A + A’ = π (r + r’2) a + π r2 + π r’2 = π r2 + r’2 + (r + r’) a
Anche il calcolo del volume del tronco di cono è analogo a quello effettuato al § 4.35
per il tronco di piramide, per cui si può dire:
il volume del tronco di cono Vt , se h ne è l’altezza, è dato dalla formula:
Vt = π (r2 + r’2 + r r’) h / 3
4.45 Sfera e superficie sferica
Si chiama sfera un solido ottenuto facendo compiere una rotazione completa di un
semicerchio attorno al suo diametro.
B
La superficie generata dalla semicirconferenza
ACB, durante la rotazione, si chiama superficie
sferica.
Il centro ed il raggio della semicirconferenza sono.
C
rispettivamente, il centro ed il raggio della sfera.
Poiché tutti i punti della superficie sferica hanno la
stessa distanza dal centro della sfera, la precedente
A
definizione può essere modificata come segue:
La superficie sferica è il luogo dei punti dello spazio che hanno la medesima
distanza da un punto fisso, detto centro.
Un segmento che unisce due punti qualsiasi della superficie sferica si chiama corda
della sfera
Le infinite corde che passano per il centro si chiamano diametri della sfera.
Le rette che passano per il centro sono dette rette diametrali ed i punti in cui una
qualsiasi di queste rette interseca la superficie sferica si dicono diametralmente opposti.
4.46
Posizioni relative di un piano e di una superficie sferica
Un piano ed una superficie sferica di centro O possono assumere le seguenti reciproche
posizioni:
1°) Il piano ha dal centro O una distanza maggio re del raggio: (fig. 1)
In questo caso il piano è detto esterno alla superficie sferica.
2°) Il piano ha dal centro O una distanza congru ente al raggio: (fig. 2)
94
In questo caso il piano è detto tangente alla superficie sferica.
3°) Il piano ha dal centro O una distanza minore del raggio: (fig. 3)
In questo caso il piano è detto secante rispetto alla superficie sferica.
Se il piano secante passa per il centro della sfera viene detto piano diametrale e seziona
la superficie sferica secondo una circonferenza avente lo stesso centro e lo stesso raggio
di tale superficie. Tale circonferenza è detta circonferenza massima ed il corrispondente
cerchio è detto cerchio massimo della sfera. (fig. 4)
In tutti gli altri casi in cui il piano è secante, la circonferenza-sezione ha un raggio minore
di quello della sfera.
O r
O
r
H
H
Fig. 1
O r
H
O
Fig. 3
4.47
Fig. 2
r
Fig. 4
Area della superficie sferica
L’area della superficie sferica non è sviluppabile su un piano, però si può dimostrare che:
l’area A di una superficie sferica è equivalente a quattro volte la misura di un suo
cerchio massimo di raggio r , per cui la formula è:
A = 4 π r2
da cui si ricava:
r = √A/4π
4.48 Volume della sfera
95
Anche per il volume della sfera si può dimostrare che esso è equivalente ad un cono
avente il raggio di base congruente al diametro della sfera (2 r) e l’altezza
congruente al raggio della stessa sfera, per cui, indicando con V il volume del cono
che è anche quello della sfera, la formula è:
V = π ( 2 r )2 / 3 = π 4 r2 r = 4 π r3 /3
da cui si ricava:
r = 3√ e V / 4 π
4.49
Parti della superficie sferica e della sfera
Secando una superficie sferica con un
piano ognuna delle due parti in cui essa
viene divisa si chiama calotta sferica.
Invece le due parti corrispondenti della
sfera si chiama segmento sferico ad
una base.
Calotta sferica
Segmento sferico
ad una base
Calotta sferica
L’altezza di una calotta sferica e di un
segmento sferico ad una base è la parte
del diametro della sfera, perpendicolare
al piano secante, compreso tra il piano
suddetto e la calotta.
Zona
sferica
Se i piani secanti sono due la parte di
superficie sferica compresa fra essi è
detta zona sferica, mentre la parte di
sfera corrispondente è detta segmento
sferico a due basi.
Fuso sferico
Segmento
sferico a
due basi
Spicchio sferico
La parte di superficie sferica compresa
due semipiani aventi l’origine comune
in un diametro si dice fuso sferico mentre
la parte corrispondente della sfera è detta
spicchio sferico.
4.50
Altri solidi di rotazione
Si possono realizzare altri tipi di solidi di rotazione facendo compiere una rotazione
completa, ad es.:
di un triangolo rettangolo attorno all’ipotenusa ( fig. 1 )
di un triangolo equilatero attorno ad un lato ( fig. 2 )
di un trapezio isoscele attorno alla sua base maggiore ( fig. 3 )
96
di un trapezio rettangolo attorno alla sua base maggiore ( fig. 4 )
Fig. 1
Fig. 2
Fig. 3
Fig. 4
4.51 LE TRASFORMAZIONI GEOMETRICHE NELLO SPAZIO
Si dice trasformazione nello spazio in se stesso ogni corrispondenza biunivoca che
associa punti dello spazio a punti dello spazio.
4,52
Le isometrie
Una isometria nello spazio è una particolare corrispondenza biunivoca che
conserva la distanza di punti corrispondenti, cioè: ad ogni coppia di punti A e B
dello spazio, associa due punti A’ e B’ in modo che il segmento AB sia
congruente al segmento A’B’
Una trasformazione che ad ogni punto dello spazio associa il punto stesso si dice identità
Le caratteristiche dello spazio che restano inalterate nella trasformazione si dicono
invarianti.
Un elemento di una trasformazione ( punto, retta, piano e in generale qualunque figura
geometrica ) che ha per trasformato se stesso viene detto unito.
Seguono le principali isometrie nello spazio97
4.53
La simmetria centrale
Detto O un punto dello spazio, si chiama
simmetria centrale di centro O la
trasformazione che ad ogni punto P
dello spazio associa un punto P’,
tale che O sia il punto medio di PP’
P’
O
P
I punti P e P’ sono detti simmetrici rispetto al punto O.
La simmetria centrale gode, oltre alle proprietà di tutte le isometrie, delle proprietà
seguenti:
• Un piano si trasforma in un piano ad esso parallelo.
• Una retta si trasforma in una retta ad essa parallela.
• Una retta passante per il centro di simmetria è unita.
• Un piano passante per il centro di simmetria è unito.
• La simmetria centrale è involutoria.
O
La simmetria centrale nello spazio gode di tutte
le proprietà di quella nel piano , tranne una:
anche se due segmenti o due angoli che si corispondono sono congruenti, non si può dire
che due figure dello spazio, simmetriche rispetto ad un punto, sono congruenti perché non
esiste un movimento rigido che permetta di sovrapporle. ( v. figura)
4,54
La simmetria assiale
Se r è una retta nello spazio e P un punto che non le appartiene, si chiama simmetria
assiale di asse r la trasformazione che ad ogni punto P dello spazio, non
appartenente ad r, associa il punto P’ tale che il segmento PP’ sia perpendicolare
ad r ed il suo punto medio H appartenga ad r.
r
( Se P appartenesse ad r il suo simmetrico sarebbe ancora P)
La simmetria assiale gode delle seguenti proprietà:
P
H
• Ogni punto dell’asse è unito.
• Ogni retta perpendicolare all’asse è unita.
- Ogni piano perpendicolare all’asse è unito.
• Ogni piano passante per l’asse è unito.
• La simmetria assiale è involutoria.
• Figure che si corrispondono in una simmetria assiale sono congruenti.
4.55
La simmetria ortogonale
P
Se α è un piano e P un punto che non gli appartiene
e se si indica con H il punto di intersezione della
perpendicolare per P al piano con il piano stesso,
98
P’
il punto P’, posto sul prolungamento della semiretta PH
tale che PH ≅ P’H, si dice simmetrico rispetto al piano α.
Si chiama simmetria ortogonale o rispetto a un piano,
la trasformazione che ad ogni punto P dello spazio
associa il suo simmetrico P’ rispetto ad un dato piano α
α
P’
La simmetria ortogonale gode delle seguenti proprietà:
• I punti del piano di simmetria sono punti uniti.
• Le rette del piano di simmetria sono rette unite.
• Le rette perpendicolari al piano di simmetria sono rette unite.
• I piani perpendicolari al piano di simmetria sono uniti.
• Se una retta forma un certo angolo con il piano di simmetria la sua trasformata forma
un angolo della stessa ampiezza.
• Se una retta è parallela al piano di simmetria,
anche la sua trasformata lo è.
• Se un piano incide il piano di simmetria lungo
P
H
P’
una retta a, anche il suo trasformato passa
per a
• Se un piano è parallelo al piano di simmetria,
anche il suo trasformato lo è.
α
Anche nella simmetria ortogonale, come in quella
centrale, figure simmetriche non sono congruenti
4.56
La simmetria nei solidi
Alcuni solidi presentano delle caratteristiche particolari rispetto alle simmetrie.
Alcune di esse sono presentate nei §§ seguentl
4.56.1 Il centro di simmetria di un solido
Un punto O di un solido S è detto centro di simmetria se S è trasformato in se
stesso dalla simmetria centrale di centro O.
Un parallelepipedo (ad es. un cubo) è dotato di un centro di simmetria che è il punto in cui
si incontrano le diagonali.
La piramide ne è priva.
La sfera ha come centro
di simmetria il suo centro.
Il cilindro ha il centro di
simmetria nel punto di
mezzo dell’altezza.
4.56.2
Gli assi di simmetria di un solido
99
Un solido S ammette come asse di simmetria una retta r se la simmetria
assiale di asse r trasforma S in se stesso.
Un cubo ha 13 assi di simmetria:
• le congiungenti i centri di due facce
opposte (sono 3);
• le congiungenti i punti medi di due
spigoli opposti ( sono 6);
• le congiungenti di due vertici opposti
( sono 4);
V
O
O
Una piramide di vertice V che abbia
come base un poligono dotato di
centro di simmetria O ammette come
asse di simmetria la retta VO
O
Il cono ha come asse di simmetria
l’asse di rotazione.
O
La sfera ha infiniti assi di simmetria:
tutte ie rette che passano per il centro.
4.56.3 I piani di simmetria di un solido
Un solido S ammette come piano
di simmetria un piano α se la
simmetria ortogonale di piano
α trasforma S in se stesso.
Un cubo ammette nove piani di
simmetria:
• il piano individuato dai punti
medi degli spigoli paralleli tra loro
(sono 3);
• i piani diagonali che sono
due per ogni coppia di facce
(sono 6);
• Il cilindro ed il cono hanno
infiniti piani simmetria che passano
per l’asse di rotazione.
La sfera ha infiniti piani di simmetria
100
che passano per il centro.
4.57
La traslazione
P’
Si chiama traslazione di vettore v la
trasformazione che ad ogni punto P
dello spazio associa il punto P’ tale che
il segmento PP’ sia equipollente a v
P
v
La traslazione gode delle seguenti proprietà:
• Non vi sono punti uniti.
• Le rette che hanno la stessa direzione di v sono unite.
• I piani che sono paralleli alla direzione di v sono uniti.
• Ad ogni piano corrisponde un piano ad esso parallelo.
• Due figure che si corrispondono in questa trasformazione sono congruenti.
4.58
La rotazione
Data nello spazio una retta r ed un angolo ab di ampiezza assegnata e preso un
qualunque punto P nello spazio, non appartenente a
r, e un piano α, passante per P, perpendicolare a
r, con O il loro punto di intersezione, si dice:
r
rotazione di asse r e ampiezza ab la
trasformazione che ad ogni punto P dello
b P’
spazio associa il punto P’, corrispondente di
O
P nella rotazione piana di ampiezza ab sul
α
a P
piano α passante per P e perpendicolare
a r e avente come centro il punto O,
intersezione di α con r
Due figure che si corrispondono in una rotazione sono congruenti.
4.59
L’omotetia e la similitudine
La definizione data per l’omotetia nella geometria piana può essere estesa all’omotetia
nello spazio.
I punti P e P’ si corrispondono in una omotetia di centro O e rapporto k ( ≠ 0 ) se
P e P’ appartengono a una retta passante per O ed è OP’ / OP = | k |.
L’omotetia di centro O e rapporto k gode delle seguenti
O
proprietà:
• Il trasformato di un piano è un piano ad esso parallelo.
• La trasformata di una retta è una retta ad essa parallela.
• Ogni piano ed ogni retta che passano per O sono uniti.
• Il trasformato di un diedro è un diedro congruente a
quello dato.
• I perimetri dei poligoni che si corrispondono stanno tra
loro nel rapporto k.
101
•
Le aree di poligoni e di figure piane che si corrispondono
stanno tra loro nel rapporto k2.
Si dice similitudine il prodotto di una omotetia con una isometria.
102
5
5.1
APPENDICi
CENNI DI LOGICA MATEMATICA
Come si è visto in quanto precedentemente esposto, le figure geometriche e le loro
proprietà costituiscono l’oggetto e lo scpo della geometria.
In certi casi la verità di alcune affermazioni si può stabilire immediatamente, per intuizione
Ad es.: Due punti appartengono ad una sola retta.
Un punto su una retta la divide in due parti.
In altri casi per dimostrare la verità di certe affermazioni si deve far ricorso al
ragionamento.
Ad es.: In un poligono la somma degli angoli esterni è uguale a due angoli piatti.
Due triangoli sono congruenti se hanno congruenti due angoli ed il lato ad essi
adiacente.
Compito della logica è, tra l’altro, quello di dare delle regole deduttive, per mezzo delle
quali, partendo da premesse vere, si perviene sicuramente a conclusioni vere.
5.2
Proposizioni
L’oggetto della logica è pertanto il linguaggio di cui l’elemento fondamentale è la
proposizione, che è un insieme di termini linguistici per i quali si può parlare di
vero o di falso.
Ad es.si può dire che è vera l’affermazione: Il sole sorge all’alba.
Si può dire che è falsa l’affermazione: Il cavallo ruggisce.
Non si sa invece se sia vera o falsa l’affermazione: Il nipote di Marco si chiama Roberto.
5.3
Proposizioni atomiche e molecolari
Le proposizioni, le cui componenti non hanno la proprietà di essere vere o false, si dicono
atomiche, come ad es. la proposizione: Il pentagono ha cinque lati,
che è una proposizione atomica in quanto in essa non è possibile isolare dei termini che
servano per creare altre proposizioni.
Invece una affermazione del tipo: La mucca è un mammifero, l’aquila un uccello,
è del genere molecolare. perchè. si possono isolare due proposizioni atomiche:
La mucca è un mammifero. e L’aquila è un uccello.
5.4
Connettivi ed operazioni elementari
Due o più proposizioni atomiche possono essere collegate mediante degli elementi
linguistici quali ad es, e, o, dunque, perciò, se e solo se, ecc. e trasformate in
proposizioni molecolari. Ad es.:
C’è il sole, dunque è giorno.
Un numero è pari se e solo se è divisibile per due.
Dall’analisi di tali proposizioni appare evidente che con esse si possono effettuare certe
operazioni mediante le quali a due proposizioni se ne fa corrispondere una terza, nuova.
Questi elementi sono detti connettivi ad ognuno dei quali corrisponde un’operazione
elementare
103
5.5
Congiunzione di due proposizioni
La congiunzione è l’operazione logica per mezzo della quale, date due proposizioni, si
forma con queste una nuova proposizione che viene considerata:
vera se le due proposizoni sono entrambe vere;
falsa negli altri casi ( cioè anche se una sola delle due proposizioni è falsa ).
Esempi: Dalle seguenti proposizioni:
Manzoni ha scoperto l’America; (f)
Manzoni ha scritto “ I promessi sposi”; (v)
8 è un numero pari; (v)
8 è un multiplo di 4. (v)
si ottengono le seguenti:
8 è un numero pari ed multiplo di 4; (v)
Manzoni ha scritto “I promessi sposi” ed ha scoperto l’America. (f)
5.6
Alternazione di due proposizioni
L’alternazione è l’operazione logica per mezzo della quale, date due proposizioni, con
queste si forma una nuova proposizione che viene considerata:.
falsa se le due proposizioni sono entrambe false
vera negli altri casi ( cioè quando una almeno delle proposizioni è vera ).
Esempi: Dalle seguenti proposizioni:
Un triangolo ha 5 lati; (f)
Un pentagono ha 3 lati; (f)
10 è un numero pari; (v)
10 è multiplo di 3 (f)
si ottengono le seguenti:
Un triangolo ha 5 lati ed un pentagono ne ha 3; (f)
10 è un numero pari ed è multiplo di 3. (v)
5.7 Implicazione di due proposizioni
L’implicazione è l’operazione logica per mezzo della quale, date due proposizioni. dette
prima e seconda, si forma con esse una nuova proposizione che viene considerata:
falsa se la prima è vera e la seconda è falsa;
vera negli altri casi.
Esempi: Dalle seguenti proposizioni:
7 è un numero dispari; (v)
7 è un multiplo di 3; (f)
Un quadrangolo ha 5 angoli; ( f)
Un quadrangolo ha 5 lati. (f)
si ottengono le seguenti:
104
7 è un numero dispari e quindi è multiplo di 3, (f)
Un quadrangolo ha 5 angoli allora ha 5 lati. (v)
5.8
Coimplicazione di due proposizioni
La coimplicazione di due proposizioni è l’operazione logica per mezzo della quale, date
due proposizioni, si forma con esse una nuova proposizione che viene considerata:
vera se le due proposizioni sono entrambe vere;
falsa negli altri casi.
Esempi: Dalle seguenti prosizioni :
L’America è un continente; (v)
L’Europa è un continente; (v)
Firenze è la capitale d’Italia; (f)
Firenze si trova nel Sud Italia. (f)
si ottengono le seguenti:
L’America e l’Europa sono dei continenti; (v)
Firenze è la capitale d’Italia e si trova nel Sud Italia: (f)
5.9
Negazione di una proposizione
La negazione di una proposizione è l’operazione logica per mezzo della quale, data una
proposizione, se ne ottiene un’altra che è:
vera se la prima è falsa;
falsa se la prima è vera
Esempi: :
La Spagna è una penisola; (v)
La Spagna non è una penisola; (f)
Un cilindro è una figura piana; (f)
Un cilindro non è una figura piana. (v)
105
5.10
APPLICAZIONI DELL’ALGEBRA ALLA GEOMETRIA
Molte volte i problemi geometrici si possono risolvere per mezzo di equazioni che si
ottengono trasformando le relazioni di carattere geometrico, presenti negli elementi di un
problema, in relazioni algebriche.
Si parla quindi di algebra applicata alla geometria.
Quanto detto è reso possibile per il fatto che la teoria della misura, trattata nel § 3.98,
permette di tradurre problemi geometrici, cioè questioni legate a relazioni tra grandezze
geometriche, in problemi algebrici, ossia problemi che si risolvono mediante relazioni tra
numeri reali che ne esprimono le misure.
5.11
Il metodo analitico
Una delle prime operazioni da fare per giungere alla soluzione di un problema è quella di
tracciare un disegno, il più accurato e preciso possibile, in cui siano evidenziate le
principali proprietà.
Il metodo analitico è caratterizzato da varie fasi:
1°) Scelta dell’incognita o delle incognite.
2°) Traduzione di un problema in un’equazione.
Partendo dalle relazioni tra gli elementi noti e quelli incogniti ed applicando gli assiomi, i
teoremi, i corollari conosciuti, si scrivono una o più equazioni, in una o più incognite,
tenendo presente che, ovviamente, il numero delle incognite deve essere uguale a quello
delle equazioni.
3°) Risoluzione dell’equazione o del sistema di equazioni.
Tale operazione si effettua con i metodi studiati nell’algebra.
4°) Discussione delle soluzioni ottenute.
Tale operazione consiste nella verifica delle soluzioni delle equazioni per valutare se esse,
tutte o in parte, sono accettabili, non solo dal punto di vista algebrico, ma soprattutto da
quello geometrico: delle soluzioni negative possono essere valide algebricamente ma non
geometricamente: infatti non esistona, ad es. dei segmenti negativi.
5.12
Interpretazione algebrica dei teoremi di Pitagora e di Euclide.
Ricordando i suddetti teoremi, esaminati dal punto di vista geometrico, considerando delle
figure piane come quadrati e rettangoli, si cerca adesso di trovare per tali teoremi una
soluzione algebrica.
1°) Teorema di Pitagora.
Dato un triangolo rettangolo in cui vengono indicati con: a la misura dell’ipotenusa e con
106
b e c quelle dei cateti, il teorema di Pitagora può
essere scritto, in forma algebrica, con l’uguaglianza
a2 = b2 + c2
che può essere trasformata in:
a = √ b 2 + c2
Inoltre si possono ricavare:
b2 = a2 – c2
e
c2 = a2 – b2
b = √ a 2 – c2
e
c = √ a2 . b2
c
B
b
a
C
2°) I teoremi di Euclide
Considerando di nuovo il triangolo del punto 1°) in cui sono stati aggiunti: il segmento AH,
la cui misura è h, della perpendicolare dal punto A all’ ipotenusa BC e le misure d ed
e delle proiezioni ortogonali dei cateti, rispettivamente
A
c e b, su a, il primo teorema di Euclide può essere
scritto in forma algebrica nel modo seguente:
c
b
b2 = a e
e
c2 = a d
da cui si possono ricavare:
e
c = √ad
d
e
b = √ae
2
2
a = b /e
a = c /d
B
a H
C
e = b2 / a
d = c2 / a
Il secondo teorema di Euclide si può tradurre nella seguente forma algebrica:
h2 = d e
da cui si possono ricavare
e
e = h2 / d
d = h2 / e
3°) Il teorema di Pitagora generalizzato
Considerando ora un triangolo non rettangolo con l’angolo nel vertice A acuto e
indicando con h la misura dell’altezza CH
C
relativa alla base AB, con riferimento al
triangolo rettangolo BHC si ha:
a2 = h2 + (c – d)2
b
h
a
e con riferimento al triangolo rettangolo AHC
si ha
h2 = b2 - d2
A
c
H
B
Sostituendo l’ultima espressione in quella
precedente si ottiene
a2 = b2 – d2 + (c – d)2 = b2 – d2 + c2 – 2 c d + d2
da cui, semplificando deriva:
a2 = b2 + c2 – 2 c d
che è la formula del teorema di Pitagora generalizzato, quando l’angolo in A è
acuto.
Quando invece l’angolo in A è ottuso la formula diventa:
a2 = b2 + c2 + 2 c d
Il teorema di Pitagora generalizzato può quindi essere enunciato nel modo seguente:
107
In un triangolo qualsiasi il quadrato costruito su un lato opposto ad un angolo acuto
è equivalente alla somma dei quadrati costruiti sugli altri due lati, diminuita del
doppio del rettangolo formato da uno di questi e dalla proiezione dell’altro su esso.
Invece il quadrato costruito su un lato opposto ad un angolo ottuso è equivalente
alla somma dei quadrati costruiti sugli altri due lati, aumentata del doppio del
rettangolo formato da uno di questi e dalla proiezione dell’altro su esso.
4°) Triangolo rettangolo isoscele
a
Dato un triangolo rettangolo isoscele con la misura di
un cateto uguale ad l e con la misura dei’ipotenusa
uguale ad a, per quanto esposto al § 3.126 si ha:
a = √2 l
l
C
5°) Triangolo equilatero
Applicando il teorema di Pitagora a uno dei due triangoli
rettangoli in cui il triangolo equilatero viene diviso
dall’altezza h, si può scrivere:
h2 = l2 – ( l / 2 )2
da cui
h = √ l 2 – (l / 2)2 = √ 3 l 2 / 4 = √ 3 l / 2
Essendo l’area del triangolo equilatero S = l h / 2
trovato si ottiene
S = √ 3 l 2/ 4
l
h
A
H
B
sostituendo ad h il valore appena
6°) Il raggio della circonferenza circoscritta ad un triangolo
C
Osservando la figura si nota che i triangoli
a
rettangoli ACH e DCB sono simili per il
b
h
B
primo criterio perché hanno gli angoli AHC
H
e CBD retti; gli angoli in A e in D
A
c O
congruenti perché sottendono lo stesso
e
arco BC per cui ACH ≅ DCB
d
Si può quindi scrivere:
CD / AC = BC / CH
D
e, passando alle misure, sj ha:
d/b = a/h
(d = 2 r)
Se si indica con S l’area del triangolo ABC e con r il raggio della circonferenza di
centro O circoscritta al triangolo, poiché il prodotto dei medi della suddetta proporzione,
è uguale a quello degli estremi, si ottiene:
2rh = ba
Se si moltiplicano entrambi i membri per c si ha:
2rhc = bac
Ma poiché il prodotto h c è il doppio dell’area S del triangolo ABC, si può scrivere:
2r2S = bac
da cui
r = abc/4S
e
S = abc/4r
7°) Il lato del quadrato inscritto in una circonf erenza in funzione del raggio
Mediante il teorema di Pitagora applicato ad uno dei due triangoli rettangoli con i cateti l,
108
determinati dalla diagonale BD, si ottiene:
(l=2r)
l 2 + l 2 = 2 l 2 = 4 r2
e quindi
D
l
C
O
l = √2 r
A
B
8°) Il lato del triangolo equilatero in funzione del raggio
C
Applicando il teorema di Euclide al triangolo ACD si può
scrivere:
AC2 = CD• CH
Essendo AC = l il lato del triangolo ABC; CD = 2 r e
CH = h. l’altezza dei triangolo dato, che per il punto 5°) A
è
h = √3 l/2
l’espressione precedente diventa:
l2 = 2r√3l/2
cioè
l = √3 r
l
h
O
H
r
B
D
9°) Il lato dell’esagono regolare inscritto in un a circonferenza, in funzione del
raggio
Considerando uno dei 6 triangoli tra loro congruenti che
formano l’esagono ABCDEF, che sono isosceli, essendo
OA = OB = OC….. ecc raggi della circonferenza, e che
sono anche equilateri ed equiangoli perché, come è facile
verificare, i tre angoli di ogni triangolo sono tutti di 60°, il
lato dell’esagono è congruente al raggio della circonferenza
cioè è
l = r
r
O
l
10°) Il lato del poligono regolare di n lati ci rcoscritto a una circonferenza
Se AB è il lato di un poligono regolare di n lati
C
H
D
circoscritto ad una circonferenza e CD il lato di
un poligono regolare, pure di n lati, inscritto nella
A
K
B
stessa circonferenza, considerando il raggio OH
perpendicolare ad entrambi i lati suddetti, si
nota che i triangoli AOB e COD sono simili
essendo gli angoli ordinatamente congruenti.
O
Ricordando che in due triangoli simili due lati
corrispondenti sono proporzionali alle altezze,
si può scrivere: CD / AB = OH / OK in cui OH e OK sono le altezze dei due triangoli.
Se ln ed Ln sono rispettivamente le misure dei lati del due poligoni, inscritto e
circoscritto, ed r = OA la misura dei raggio della circonferenza inscritta, la misura
dell’apotema risulta:
OK = √ r2 – (l / 2)2
e la precedente proporzione diventa:
Ln / ln = r / √ r2 – (l/2)2
e quindi
Ln = ln r / √ r2 – (l / 2)2
109
5.13
FORMULARIO
5.13.1 FORMULARIO DI GEOMETRIA PIANA
NOME
FIGURA
SIMBOLI
e
FORMULE
Triangolo qualunque
B
c
h
ma
A
p = semiperimetro
S = area
S=bh/2
r = rag. circ. inscr.
R = rag, circ. circoscr.
ma = mediana del lato a
sa = bisettrice dell’angolo
in A
a
b
2 p = a+b+c
S = √p(p-a)(p-b)(p-c)
r=S/p
R =abc / 4S
ma = √2b2 + 2c2 – a2 / 2
sa = 2 √ bcp(p-a) / (b+c)
Triangolo rettangolo
C
√2 c
30°
m
2c
b
√3 c
a
h
c
45°
c
n
60°
A
c
B
c
a = √ b 2 + c2
b2 = a m
b = √ a2 – c2
c = √ a2 – b2
c2 = a n
h2 = m n
S=bc/2= ah/2
r = (b + c – a) / 2
R=a/2
Triangolo equilatero
A
l
h r
R
B
l = lato
h = altezza
S = area superf.
r = rag. circ. inscr.
R = rag. circ. circoscr.
l = 2 h √ 3 / 3 = √4 S / √3
h=l√3/2
S = l 2√ 3 / 4
r=h/3=l√3/6
R=2h/3=l√3/3
i/2 C
Rettangolo
h
R
d
b
b = base
h = altezza
d = diagonale
S = area superf.
R = raggio circ. circoscr.
110
b=S/h
h=S/b
d = √ b2 + h2
S=bh
R=d/2
Rombo
D
C
l = lato
h = altezza
d e d1 = diagonali
S = area superf.
r = raggio circ. Inscr.
d1 d
h
l
r
A
l = √ d2 + d12 / 2
h=S/l
S = l h = d d1 / 2
r = h / 2 = d d1 / 2 l
B
Quadrato
l
l= d√2 /2 =√S
d=l√2
S=l2
l = lato
d = diagonale
S = area superf.
d
Trapezio qualunque
b1 e b2 = basi
h = altezza
S = area superf.
D
S = (b1 + b2) h / 2
b2 C
h
M
N
B
A
b1
Le diagonali si tagliano in parti proporzionali alle basi.
MN congiungente i punti medi dei lati non paralleli è parallelo alle due
basi ed è uguale alla loro semisomma: (b1 + b2) / 2.
Trapezio isoscele
D
K
P
C
.
A
H
R
R = raggio circ. circoscr.
Le diagonali sono congruenti e si tagliano in parti
rispettivamente congruenti e proporzionali alle basi.
Il trapezio è diviso dalle diagonali in due triangoli
isosceli simili e due triangoli congruenti.
B Avendo gli angoli opposti supplementari è
inscrittibile in una circonferenza.
Trapezio isoscele o rettangolo circoscritto ad una circonferenza
D
K
C
E
O
A
H
r
Il triangolo COB è rettangolo in O e il raggio
r è medio proporzionale tra HB e KC
rispettivamente congruenti a BE e CE.
B
111
Trapezio isoscele circoscritto ad una semicirconferenza
D
C
Il lato obliquo è uguale a metà della base maggiore
E
perché sono tra loro congruenti i triangoli
rettangoli AEO e AFD.
A F O
B
Lato ln , apotema an , ed area Sn di poligoni regolari di n lati, inscritti in un
cerchio di raggio r
l3 = r √ 3
a3 = r / 2
S3 = 3 l 2 √ 3 / 4
l4 = r √ 2
a4 = r √ 2 / 2
S4 = 2 r2
l5 = r √ 10 – 2 √ 5 / 2
a5 = r (√ 5 + 1) / 4
S5 = r2 √ 10 + 2 √ 5
l6 = r
a6 = r √ 3 / 2
S6 = 3 r2 √ 3 / 2
l8 = r ( √ 2 - √ 2 )
a8 = r √ 2 + √ 2 / 2
S8 = 2 r2 √ 2
l10 = r ( √ 5 – 1 ) / 2
a10 = r √ 10 + 2 √ 5 / 4
S10 = 5 r2 √ 10 – 2 √ 5 / 4
l15 = r (√ 10 + 2 √ 5 - √ 15 - √ 3 ) / 4
l2n = √ 2 r2 – r √ 4 r2 – ln2
Lato Ln ed area Sn di poligoni regolari di n lati, circoscritti ad un cerchio di
raggio r
S3 = 3 r2 √ 3
S4 = 4 r2
S6 = 2 r2 √ 3
L3 = 2 r √ 3
L4 = 2 r
L6 = 2 r √ 3
Ln = 2 r ln / √ 4 r2 – ln2
Circonferenza e cerchio
lc = misura della lunghezza della circonferenza
r = lc / 2 π
S = π r2
r=√S/π
lc = 2 π r
Arco di circonferenza
la = misura della lunghezza dell’arco
la = π r n / 180° ( n = misura dell’angolo che sottend e l’arco in gradi )
la = r α
(α= “
“
“
“
“
“ “ radianti )
Settore circolare
la
Segmento circolare
Ss = area del settore
Sg = “
“ segmento
c = misura della corda
s=
“
“ saetta
la
r
s
c
A
B
r
Ss = π r2 n / 360° = l a r / 2 = α r2 / 2
Sg = Ss – area del triangolo AOB =
O
la r – lc (r – s)
112
/2
c=√4s(2r–s)
s = r - √ r2 – lc2 / 4
5.13.2
FORMULARIO DI GEOMETRIA SOLIDA
NOME
FIGURA
SIMBOLI
e
FORMULE
Prisma retto
d
h
c
a
b
p = perimetro di base
h = altezza
B = base
Sl = area superf. lat.
St = area superf. tot
V = volume
Cubo
d
R
l
r
p = a +b + c +…= Sl / h
h = St / p = V / B
B=V/h
Sl = p h
St = Sl + 2 B
V=Bh
l = lato
d = diagonale
r = ragg. sfera inscr.
R = ragg. sfera circoscr.
Sl = area superf. later.
St = area superf. tot.
V = volume
l = d√ 3 / 3 = 3√ V
d=l√3
r=l/2
R=l√3 /2
Sl = 4 I 2
St = 6 l 2
V=l3
a e b = lati base
c = altezza
c d = diagonale
B = area base
b Sl = area superf. later.
St = area superf. tot.
V = volume
d = √ a 2 + b 2 + c2
B=ab
Sl = 2 (a + b) c
St = 2(a b + a c + b c)
V=abc
Parallelepipedo rettangolo
d
a
Piramide retta
p = perimetro base
a = apotema
h = altezza
B = area base
Sl = area superf. later.
St = area superf. tot.
V = volume
h
a
p = 2 Sl / a
a = 2 Sl / p
h=3V/B
B=3V/h
Sl = p a / 2
St = Sl + B
V= Bh/3
Tronco di piramide retta
h
a
P e p = perimetri di base
a = apotema
h = altezza
B e b = area superf. basi
Sl = area superf.later.
St = area superf. tot.
V = volume
113
P+p = 2 Sl / a
a = 2 Sl / (P + p)
h =3 V / (B + b + √ B b)
Sl = (P + p) a / 2
St = Sl + B + b
V = h(B+b+√ B b ) / 3
Tetraedro regolare
l = h √ 6 / 2 = 2 √√ 3 St / 3 = 2 r √ 6
l = √ 3√3 St / 3 = 3√ 6 √ 2 V = 2 R √ 6 / 3
h = altezza
h=l√6/3
r = ragg. sfera inscr.
r = l √ 6 / 12
R = ragg. sfe. circoscr. R = l √ 6 / 4
Sl = area superf. later. Sl = 3 l 2 √3 / 4
St = area superf. tot.
St = l 2 √ 3
V = volume
V = l 3 √ 2 / 12
l = lato
h
R
l
r
Ottaedro regolare
l = √ S √ 3 / 6 = 3√ 3 √ 2 V / 2
l=r√6 =R√2
r = raggio sfera inscr.
r=l√6 /6
R = raggio sfera circoscr. R = l √ 2 / 2
S = area superf. tot.
S=2l2√3
V = volume
V=l3√2/3
l = lato
l r
R
Cilindro
r = raggio
h = altezza
B = area base
Sl = area superf. later.
St = area superf. tot.
V = volume
r
h
r = Si / 2 π h = √ V / π h
h = Sl / 2 π r = V / π r2
B = π r2
Sl = 2 π r h
St = 2 π r (h + r)
V = π r2 h
Cilindro equilatero
r
H
r = raggio
r = √ Sl / 4 π = √ St / 6 π = 3√ V / 2 π
h = altezza
h=2r
Sl = area superf. later. Sl = 4 π r2
St = area superf. tot.
St = 6 π r2
V = volume
V = 2 π r3
Cono
a h
r
h = altezza
a = apotema
r = raggio base
Sl = area superf. later.
St = area superf. tot.
V = volume
114
h = 3 V / π r2
a = Sl / π r
r = Sl / π a = √ 3 V / π h
Sl = π r a
St = π r ( a + r)
V = π r2 h / 3
Cono equilatero
a = apotema
h = altezza
r = raggio base
a
h
r
Sl = area superf. later.
St = area superf. tot.
V = volume
a=2r
h=r√3
r = √ Sl / 2 π = √ St / 3 π =
= 3√ V √ 3 / π
Sl = 2 π r2
St = 3 π r2
V = π r3 √ 3 / 3
Tronco di cono
r
a
h
R
a = apotema
h = altezza
r e R = raggi basi
Sl = area superf. later.
St = area superf. tot.
V = volume
Sl = π a (R + r)
St = Sl + π r2 + π R2
V = π h (R2 + r2 + R r) / 3
Sfera e sue parti
r
d
r = raggio sfera
d = diametro sfera
S = area superf.
V = volume
r = √ S / 4 π = 3√ 3 V / 4 π
d=√S/π
S = 4 π r2 = π d2
V = 4 π r3 / 3 = π d2 / 6
Area calotta sferica e zona sferica
h
r = raggio sfera
h = altezza calotta
o zona
S = area superf. calotta
o zona
S=2πrh
h
Area fuso sferico
l
n = ampiezza in gradi
α = ampiezza in radianti
l = misura arco equatoriale
S = area superf.
S = π r2 n / 90 =
= 2 r2 α = 2 r l
115
Volume spicchio sferico
n = ampiezza in gradi
α = ampiezza in radianti
S = area superf. fuso
V volume
V = π r2 n / 270 = 2 π r2 α
=Sr/3
\
Volume segmento sferico a due basi
r2
r1
r1 e r2 = raggi basi
h = altezza segmento
V = volume
V = π h (r12 + r22 ) / 2 + π h2 / 6
h
Volume segmento sferico ad una base
r = raggio sfera
h = altezza segmento
V = volume
V = π h2 (3 r – h) / 3
h
Volume settore sferico
h
r
r = raggio sfera
h = altezza calotta
V = volume
V = 2 π r2 h / 3
Volume anello sferico
c = corda che limita il segmento circolare
h = altezza zona sferica
V = volume
c
V = π c2 h / 6
h
116
INDICE
1 INTRODUZIONE
3
2 INSIEMI
3
2.1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
2.10
2.11
2.12
2.13
2.14
2.15
2.16
2.17
2.18
2.19
2.20
2.21
2.22
2.23
2.24
2.25
Concetto di insieme
Elenco degli insiemi più frequenti
Alcune definizioni
Relazioni di uguaglianza o di equivalenza tra elementi e tra insiemi
Sottoinsiemi – Relazione di inclusione
Operazioni con gli insiemi
Insieme delle parti
Coppie ordinate
Prodotto cartesiano
Relazioni tra gli elementi di un insieme
Corrispondenze tra insiemi
Corrispondenze biunivoche
Corrispondenza inversa
Corrispondenza di Talete
Composizione di mappe
Elementi uniti di una corrispondenza – Identità
Corrispondenze involutorie
Partizione di un insieme e sue proprietà
Relazione di equivalenza
Relazione d’ordine
Proprietà degli ordinamenti totali
Operazioni e strutture algebriche – Legge di composizione
Monoidi
Gruppi
Sottoinsieme stabile
3
4
4
5
5
5
6
6
6
7
7
7
7
8
8
8
9
9
9
11
11
11
12
12
13
3 GEOMETRIA NEL PIANO
15
3.1
3.2
3.3
3.4
3.5
3.6
3.7
3.8
3.9
3.10
3.11
3.12
3.13
3.14
15
15
15
15
15
16
16
16
17
17
17
17
17
18
Definizioni
Enti primitivi
Assiomi o postulati
Alcuni assiomi fondamentali
Ipotesi, tesi, dimostrazione, teorema
CorollarI
Le figure geometriche
La congruenza
La retta e le sue proprietà
La retta orientata
Le semirette
Il segmento
Confronto tra due segmenti
Somma di due o più segmenti
117
3.15 Proprietà della somma di segmenti
3.16 Multipli e sottomultipli di un segmento
3.17 Differenza tra due segmenti
3.18 Distanza tra due punti – Spezzata
3.19 Punto medio di un segmento
3.20 Il piano e le sue proprietà
3.21 Il semipiano
3.22 La circonferenza e le sue parti
3.23 L’angolo
3.24 Angoli concavi e angoli convessi
3.25 Angolo piatto e angolo giro
3.26 Angoli consecutivi, adiacenti e opposti al vertice
3.27 Trasporto di un angolo
3.28 Confronto tra due angoli
3.29 Somma di due o più angoli e sue proprietà
3.30 Multipli e sottomultipli di un angolo
3.31 Differenza di due angoli
3.32 Angoli supplementari
3.33 Angolo retto
3.34 Bisettrice di un angolo
3.35 Angoli acuti e ottusi
3.36 Rette perpendicolari
3.37 Asse di un segmento
3.38 Perpendicolare da un punto a una retta
3.39 Rette parallele
3.40 Parallela per un punto a una retta
3.41 Angoli formati da due rette parallele tagliate da una trasversale
3.42 Distanza tra due rette parallele
3.43 Rette parallele tagliate da due trasversali – Teorema di Talete
3.44 Divisione di un segmento in parti uguali
3.45 Poligoni
3,46 Poligoni concavi e convessi
3.47 Triangoli e loro proprietà
3.48 Classificazione dei triangoli rispetto ai lati
3.49 Proprietà dei triangoli
3.50 Somma degli angoli interni di un triangolo
3.51 Somma degli angoli interni di un poligono convesso
3.52 Somma degli angoli esterni di un poligono convesso
3.53 Classificazione dei triangoli rispetto ai lati
3.54 Triangolo scaleno
3.55 Triangolo isoscele
3.56 Triangolo equilatero
3.57 Triangolo rettangolo
3.58 Elementi notevoli di un triangolo
3.58.1 Altezze – Ortocentro
3.58.2 Bisettrici dei tre angoli di un triangolo – Incentro
3.58.3 Assi dei tre lati di un triangolo
3.58.4 Mediane dei tre lati di un triangolo – Baricentro
118
18
19
19
19
19
19
19
20
20
20
20
21
21
21
22
22
22
22
23
23
23
23
24
24
24
25
25
25
26
26
26
27
27
28
28
28
28
29
29
29
29
29
30
30
30
30
30
31
3.59 Isometrie nel piano
3.60 Simmetria assiale
3.61 Traslazione
3.62 Rotazione
3.63 Simmetria centrale
3.64 Congruenze
3.65 I criteri di congruenza dei triangoli
3.66 Primo criterio di congruenza dei trtangoli
3.67 Secondo criterio di congruenza dei triangoli
3.68 Terzo criterio di congruenza dei triangoli
3.69 Criteri di congruenza dei triangoli rettangoli
3.70 Quadrilateri
3.71 Trapezi
3.72 Parallelogrammi
3.73 Parallelogrammi particolari
3.74 Rettangolo
3.75 Rombo
3.76 Quadrato
3.77 Criteri di congruenza dei poligoni
3.78 Formula di Erone per i poligoni
3.79 I luoghi geometrici
3.80 Circonferenza e cerchio
3.81 Angolo al centro
3.82 Angolo alla circonferenza
3.83 Proprietà delle corde
3.84 Elementi del cerchio
3.85 Posizioni reciproche tra rette e circonferenze
3.86 Proprietà della tangente alla circonferenza
3.87 Posizioni reciproche di due circonferenze
3.88 Poligoni inscritti in una circonferenza
3.89 Poligoni circoscritti a una circonferenza
3.90 Poligoni regolari
3.91 Equivalenza delle superfici piane
3.92 Poligoni equivalenti
3.93 Somme e differenze di superfici
3.94 Poligoni equiscomponibili
3.95 Casi particolari di equivalenza di poligoni
3.96 Trasformazione di poligoni
3.97 I teoremi di Euclide e di Pitagora
3.97.1 Primo teorema di Euclide
3.97.2 Teorema di Pitagora
3.97.3 Secondo teorema di Euclide
3.97.4 Una applicazione del primo teorema di Euclide – Trasformazione di un
rettangolo in un quadrato ad esso equivalente
3.98 La misura
3.99 Grandezze omogenee, misurabili e continue
3.99.1 Lunghezze
3.99.2 Altre classi di grandezze omogenee e misurabili
3.100 Proporzionalità
119
31
32
32
33
33
34
34
35
35
35
36
36
37
37
38
38
38
38
38
39
39
39
40
40
41
41
42
42
42
43
43
44
44
45
45
45
45
48
50
50
50
51
52
52
53
53
53
54
3.100.1 Rapporto tra due grandezze
3.100.2 Proporzionalità tra grandezze geometriche
3.100.3 Proporzionalità diretta
3.100.4 Proporzionalità inversa
3.101 Misura dei segmenti
3.102 Misura degli angoli
3.103 Operazioni sulle misure degli angoli
3.104 Addizione
3.105 Sottrazione
3.106 Moltipliocazione per un numero intero
3.107 Divisione per un numero intero
3.108 Moltiplicazione per una frazione
3.109 Formule per il calcolo dell’area di un poligono
3.110 Area del rettangolo
3.111 Area del quadrato
3.112 Area del parallelogrammo
3.113 Area del rombo
3.114 Area del triangolo
3.115 Misura dell’altezza relativa all’ipotenusa in un triangolo rettangolo
3.116 Formula di Erone per calcolare l’area di un triangolo qualsiasi, note le
misure dei suoi lati
3.117 Area del trapezio
3.118 Area di un poligono circoscritto a una circonferenza
3.119 Misura del raggio della circonferenza inscritta in un poligono
3.120 Misura del raggio della circonferenza inscritta in un triangolo rettangolo
3.121 Riformulazione dei teoremi di Pitagora e di Euclide
3.122 Teorema di Pitagora
3.123 Primo teotrema di Euclide
3.124 Secondo teorema di Euclide
3.125 Applicazioni del teorema di Pitagora
3.126 Misura della diagonale di un quadrato in funzione del lato
3.127 Misure dei lati di un triangolo rettangolo isoscele
3.128 Misura dell’altezza di un triangolo equilatero in funzione del lato
3.129 Misurta dei lati di un triangolo rettagolo con gli angolo acuti di 30° e 60°
3.130 Misura della circonferenza
3.131 Lunghezza di un arco di circonferenza
3.132 Ares del cerchio
3.133 Area di un settore circolare e area di un segmento circolare
3.134 Le trasformazioni nel piano
3.135 Omotetia
3.136 Le equazioni dell’omotetia con centro nell’origine degli assi cartesiani
3.137 Similitudine
3.138 Criteri di similitudine dei triangoli
3.139 Primo criterio di similitudine dei triangoli
3.140 Secondo criterio di similitudine dei triangoli
3.141 Terzo criterio di similitudine dei triangoli
3.142 Triangoli simili
3.143 Criteri di similitudine dei poligoni
3.144 Alcune proprietà dei poligoni simili
120
54
54
55
56
56
56
57
57
57
58
58
58
59
59
59
60
60
60
60
60
61
61
61
61
62
62
62
62
63
63
63
63
64
64
65
65
65
66
66
67
68
68
68
69
69
70
71
72
3.145 La similitudine nelle circonferenze
3.146 Sezione aurea di un segmento
72
73
4 GEOMETRIA NELLO SPAZIO
75
4.1
4.2
4.3
4.4
4.5
4.6
4.7
4.8
4.9
4.10
4.11
4.12
4.13
4.14
4.15
4.16
4.17
4.18
4.19
4.20
4.21
4.22
4.23
4,24
4.25
4.27
4.28
4.29
4.30
4.31
4.32
4.33
4.34
4.35
4.36
4.37
4.38
4.39
4.40
4.41
4.42
4.43
4.44
4.45
75
75
75
75
76
77
77
78
79
79
79
80
80
81
81
82
82
82
82
83
83
84
84
84
85
86
86
87
88
89
89
89
90
90
91
91
91
92
92
92
93
93
94
94
Premessa
Lo spazio
I semispazi
I piani nello spazio
Posizioni reciproche di due piani nello spazio
Posizioni reciproche di due rette nello spazio
Posizioni reciproche di una retta e un piano nello spazio
Rette e piani perpendicolari
Distanza di un punto da un piano
Distanze di rette e piani
Diedri
Piani perpendicolari
Prismi
Prisma retto e prisma regolare
Area della superficie di un prisma retto
Parallelepipedo
Parallelepipedo rettangolo
Area della superficie di un parallelepipedo rettangolo
Misura della diagonale di un parallelepipedo rettangolo
Cubo
Piramidi
Piramide retta
Piramide regolare
Area della superficie laterale e totale di una piramide retta
Tronco di piramide
Poliedri
Poliedri regolari
Solidi equivalenti
Volume dei solidi
Volume del parallelepipedo rettangolo
Volume del cubo
Volume del prisma
Volume della piramide
Volume del tronco di piramide
Solidi di rotazione
Il cilindro
Area della supeficie di un cilindro
Volume del cilindro
Il cono
Area della superficie del cono
Volume del cono
Il tronco di cono
Area della superficie e volume del tronco di cono
Sfera e superficie sferica
121
4.46 Posizioni relative di un piano e di una superficie sferica
4.47 Area della superficie sferica
4.48 Volume della sfera
4.49 Parti della superficie sferica e della sfera
4.50 Altri solidi di rotazione
4.51 Le trasformazioni geometriche nello spazio
4.52 Le isometrie
4.53 La simmetria centrale
4.54 La simmetria assiale
4.55 La simmetria ortogonale
4.56 La simmetria nei solidi
4.56.1 Il centro di simmetria di un solido
4.56.2 Gli assi di simmetria di un solido
4 56.3 I piani di simmetria di un solido
4.57 La traslazione
4.58 La rotazione
4.59 L’omotetia e la similitudine
95
96
96
96
97
97
97
98
98
99
99
99
100
100
101
101
101
5 APPENDICI
103
5.1 CENNI DI LOGICA MATEMATICA
103
5.2
5.3
5.4
5.5
5.6
5.7
5.8
5.9
103
103
103
104
104
104
105
105
Proposizioni
Proposizioni atomiche e molecolari
Connettivi e operazioni elementari
Congiunzione di due proposizioni
Alternazione di due proposizioni
Implicazione di due proposizioni
Coimplicazione di due proposizioni
Negazione di una proposizione
5.10 APPLICAZIONI DELL’ALGEBRA ALLA GEOMETRIA
106
5.11 Il metodo analitico
5.12 Interpretazione algebrica dei teoremi di Pitagora e di Euclide
106
106
5.13 FORMULARIO
110
5.13.1 Formulario di geometria piana
5.13.2 Formulario di geometria solida
110
113
122