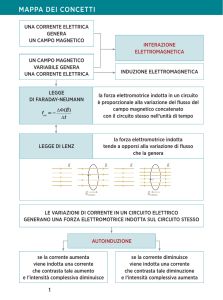
Induzione Elettromagnetica
Un campo elettrico (che induce quindi una corrente elettrica)
produce un campo magnetico.
Un campo magnetico è in grado di produrre un campo elettrico ?
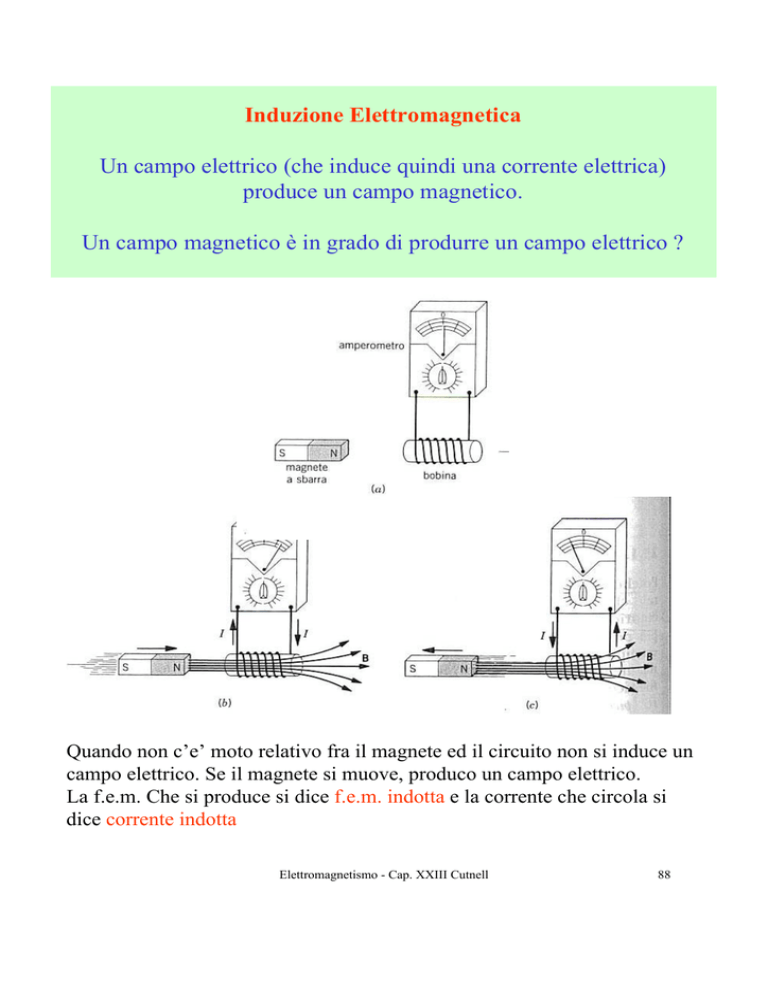
Quando non c’e’ moto relativo fra il magnete ed il circuito non si induce un
campo elettrico. Se il magnete si muove, produco un campo elettrico.
La f.e.m. Che si produce si dice f.e.m. indotta e la corrente che circola si
dice corrente indotta
Elettromagnetismo - Cap. XXIII Cutnell
88
Posso produrre una f.e.m. indotta:
• Variando l’intensità del campo magnetico
• Variando la superficie del circuito immersa nel campo magnetico
Elettromagnetismo - Cap. XXIII Cutnell
89
In alcuni casi l’effetto non è altro che la banale conseguenza della
forza di Lorentz
• Il magnete produce un campo verticale
• Il filo (le cariche) si muove orizzontalmente
• Ho una forza di Lorents F=qvB
• Induco una corrente elettrica
• Sebbene l’effetto sia locale, la corrente scorre in
tutto il filo, gli elettroni cioè si spingono e
tirano a vicenda ( .. Principio del Telegrafo)
F = qv∧ B
Elettromagnetismo - Cap. XXIII Cutnell
90
Per la grande maggioranza dei casi l’effetto è assolutamente nuovo
e non spiegabile con le leggi trovare fino ad ora
• Induco una corrente elettrica se:
• Il filo è fermo
• Il magnete è in movimento
• Il filo è fermo
• Un secondo filo è in moto
• Il filo è fermo
• Vario la corrente in un secondo filo
Variando il campo magnetico intercettato da un circuito (posso variare il
modulo, l’intensità, il verso o qualsiasi combinazioni di queste), variando
l’area di un ciruito immesso in un campo magnetico oppure variando
l’orientamento del circuito nel campo magnetico si induce nel circuito stesso
una f.e.m.
Questo fenomeno è detto induzione elettromagnetica
• Se ho un circuito aperto ⇒ Induco una corrente elettrica
⇒ Ho una forza che spinge gli elettroni
⇒ f.e.m.
• Se ho un circuito chiuso ⇒ Non può passare corrente
⇒ induco una ddp
Elettromagnetismo - Cap. XXIII Cutnell
91
Sperimentalmente si osserva che:
• Induco una f.e.m. in un circuito Se
• Vario B
• Vario la forma del circuito immersa nel campo magnetico
• Vario l’orientamento del circuito immerso nel campo magnetico
• La direzione della f.e.m. Indotta è tale da creare un campo magnetico
che si oppone alla variazione data
Elettromagnetismo - Cap. XXIII Cutnell
92
Devo trovare una osservabile che dipenda da B e dall’area
sottesa dal circuito.
La cosa più semplice è il prodotto scalare
B⋅ A
• Dove
• B è il vettore compo magnetico
• A è il vettore che ha per modulo l’area della superficie
considerata e per direzione quella normale alla
superficie stessa
• Spesso il vettore A si scrive come A n con A lo scalare
che indica la superficie ed n un versore ortogonale
alla superficie stessa
n
B ⋅ A = (B ⋅ n ) A
B
Il prodotto Φ ( B ) = B ⋅ A = ( B ⋅ n ) A si chiama flusso del campo magnetico
ed è esattamente l ' equivalente del concetto di flusso nei liquidi o gas
Elettromagnetismo - Cap. XXIII Cutnell
93
n
Φ( B) = ( B ⋅ n ) A = − A B
B
Φ( B) = ( B ⋅ n ) A = 0
θ
Φ( B) = ( B ⋅ n ) A
Φ ( B) = A B cos(θ )
Elettromagnetismo - Cap. XXIII Cutnell
94
Nel caso di superfici curve è sufficiente dividerle in areole
infinitesime cosi da poter considerare ciascuna di queste come
piatta
Φ ( B) = ∑ B ⋅ n A =
∫ B ⋅ n da
Sup
Flusso del campo Magnetico
Data una superficie qualsiasi A immersa in un campo magnetico B, si
definisce flusso di B l’integrale di superficie definito come
[Φ ] = [W ] = [V ][s ] = Weber
Φ ( B ) = ∫ B ⋅ n da
S
B ⇒ Vettore campo magnetico
n ⇒ Versore ortogonale all ' elemento di superficie da
Se la superficie A è piana e il vettore B è costante, l’integrale si riduce
al prodotto del modulo di B con il valore della superficie ed il coseno
dell’angolo sotteso tra la normale alla superficie e B
Φ( B) =
∫ B ⋅ n da = A B cos(θ )
Sup
Elettromagnetismo - Cap. XXIII Cutnell
95
Legge di Faraday Neumann Lentz
Il valore della f.e.m. Indotta su un circuito è dato dalla derivata del
flusso del campo magnetico cambiata di segno
dΦ ( B )
f .e.m. = −
dt
Esempio:
Φ( B) =
∫ B ⋅ n da = A B cos(θ ) = (L(x
0
+ vt )) B cos(0 )
Sup
Φ ( B ) = (L(x0 + vt )) B
f .e.m. = −
d
d
Φ ( B) = − (L(x0 + vt )) B = − Lv B
dt
dt
Elettromagnetismo - Cap. XXIII Cutnell
96
Esempio:
Φ( B) =
∫ B ⋅ n da = A B cos(θ ) = A B cos(θ
0
+ ωt )
Sup
f .e.m. = −
d
d
Φ ( B ) = − A B cos(θ 0 + ωt )
dt
dt
f .e.m. = A B ω sin (θ 0 + ωt )
Ho prodotto una
corrente alternata
Elettromagnetismo - Cap. XXIII Cutnell
97
Attenzione:
Se invece di un circuito ho una bobina allora devo moltiplicare per il
numero di spire. Infatti il flusso passa per ciascuna spira
dΦ ( B )
f .e.m. = − N
dt
L’energia elettrica che si ottiene per mezzo del fenomeno dell’induzione magnetica
non viene dal nulla. Il lavoro meccanico che è stato fatto per muovere la sbarra o per
far ruotare la spira è quello che ritrovo in forma di corrente elettrica.
Infatti
• Nel caso della spira devo contrastare la forza di lorentz che il filo in quanto
percorso da corrente ed immerso nel campo magnetico F = ilB che
guarda caso è diretto in direzione opposta a quella della velocità
F
• Nel caso della spira rotante devo contrastare il momento della forza dovuto
al fatto di avere una spira percorsa da corrente in un campo magnetico
Elettromagnetismo - Cap. XXIII Cutnell
98
Induttanza Propria
In un qualsiasi circuito in cui passa della corrente variabile nel tempo
1)
2)
3)
4)
La corrente varia nel tempo
Si crea un campo magnetico variabile nel tempo
Si crea a sua volta una f.e.m. indotta che contrasta la variazione
di corrente
Goto 1
Il problema può essere quindi estremamente complesso in
quanto la corrente che circola in un circuito influenza se
stessa
Per quantificare questo effetto si definisce un coefficiente L detto
induttanza propia come
L=
dΦ ( B)
di
[L] = [V ][s ] = Henry
[A]
L’induttanza propia quindi mi dice come il circuito risponde, in
termini di corrente, ad una variazione di flusso del campo
magnetico. Se le proprietà geometriche del circuito non
cambiano allora l’induttanza propria è una caratteristica tipica
del circuito.
La f.e.m. Indotta dal fenomeno dell’autoinduzione quindi si può
ricavare dalla legge di faraday Neumann Lents
f .e.m. = −
dΦ ( B )
dΦ ( B ) di
di
=−
= −L
dt
di dt
dt
Elettromagnetismo - Cap. XXIII Cutnell
99
Esempio:
Indittanza di un Solenoide
Dati solenoide
n = numero spire per unità di lunghezza
S = superficie del solenoide
l = lunghezza del solenoide
i = corrente che passa nel solenoide
B = nµ 0i
Φ ( B) = N ∫ B ⋅ n da = nl ∫ B da = nl ∫ nµ 0i da = n 2lµ 0i ∫ da
s
s
s
s
Φ ( B ) = n 2 µ 0i Sl
L=
dΦ ( B ) d 2
= n µ 0i Sl = n 2 µ 0 Sl
di
di
L dipende solo dalle cratteristiche geometriche
Elettromagnetismo - Cap. XXIII Cutnell
100
Induttanza Mutua
In una qualsiasi coppia di circuiti vicini tra loro in cui passa della
corrente variabile nel tempo
1)
2)
3)
4)
La corrente varia nel tempo in entrambi i circuiti
Si crea un campo magnetico variabile nel tempo somma dei
campi magnetici creati dai due circuiti
Si creano a loro volta, in ciascun circuito, una f.e.m. indotta che
contrasta la variazione di corrente
Goto 1
Il problema può essere quindi estremamente complesso in
quanto la corrente che circola in un circuito influenza se
stessa ed è influenzata da quello accade nelle vicinanze
M 12 =
dΦ1 ( B 2 ) dΦ 2 ( B1 )
=
= M 21
di2
di1
[M ] = [V ][s ] = Henry
[A]
Per quantificare questo effetto si definisce un coefficiente M detto
induttanza mutua come
Nel caso più semplice, in cui in un solo circuito passa corrente, allora
nel secondo si induce una f.e.m. pari a
f .e.m. = −
dΦ 2 ( B1 )
dΦ 2 ( B1 ) di1
di
=−
= −M 1
dt
di1
dt
dt
L’importanza della mutua induzione consiste nel fatto che permette il
trasferimento di energia (sotto forma di energia elettrica) da un
circuito ad un secondo circuito senza la necessita di alcun
contatto fisico. Basta che siano vicini
Elettromagnetismo - Cap. XXIII Cutnell
101
Elettromagnetismo - Cap. XXIII Cutnell
102
Esempio alla lavagna
Trasformatore
quesito 3 pg 732
esercizio 3 pg 733
Elettromagnetismo - Cap. XXIII Cutnell
103