Introduzione all`uso di Mathematica.nb

Antonino Polimeno, Marco Ruzzi
Dipartimento di Scienze Chimiche - Università degli Studi di Padova
Metodi di Calcolo per la Chimica - A.A. 2015-2016
Mathematica: un ambiente di lavoro
per l’analisi di dati sperimentali
e lo sviluppo di modelli teorici.
2
Introduzione all'uso di Mathematica.nb
Introduzione all'uso di Mathematica.nb
Sommario
Premessa
1. Introduzione
2. Nozioni di base sull’uso di Mathematica
2.1 Input e output
2.2 La funzione Help
3. Calcolo Numerico e calcolo simbolico
3.1 Preliminari
3.2 Aritmetica degli interi
3.3 Aritmetica dei razionali e degli irrazionali
3.4 Calcolo esatto e calcolo approssimato
3.5 Algebra
4. Equazioni e sistemi di equazioni lineari
4.1 Risoluzione di equazioni in forma esatta
4.2 Risoluzione di equazioni in forma approssimata
4.3 Sistemi di equazioni (cenni)
5. Funzioni reali
5.1 Premessa: l’uguaglianza
5.2 Funzioni libreria predefinite
5.3 Calcolo e rappresentazione di funzioni da in 5.4 Elementi di calcolo infinitesimale: limiti di funzioni da in 5.5 Elementi di calcolo infinitesimale: derivate di funzioni da in 5.6 Elementi di calcolo infinitesimale: primitive di funzioni da in 5.7 Calcolo di integrali definiti esatto ed approssimato
5.8 Integrali generalizzati (cenni)
5.9 Equazioni differenziali (cenni)
6. Rappresentazione di curve nel piano e nello spazio e di superfici nello spazio
6.1 Equazioni parametriche di curve in 2 e 3
6.2 Equazioni parametriche di superfici in 3
6.3 Rappresentazione di curve e superfici in forma implicita
6.4 Rappresentazione di funzioni a più variabili
7. Elementi di matematica discreta
7.1 Successioni
7.2 Serie
8. Elementi di algebra lineare
8.1 Liste
8.2 Operazioni con vettori e matrici
3
4
Introduzione all'uso di Mathematica.nb
Premessa
Mathematica è un linguaggio interpretato ad alto livello utilizzabile sia per il calcolo numerico che per il calcolo
simbolico e dotato di funzioni grafiche duttili e complete per la rappresentazione grafica bidimensionale e tridimensionale di espressioni e di dati. Esso pertanto costituisce un buon ambiente di lavoro per chi necessiti di uno
strumento potente, completo e versatile per eseguire analisi di dati, sviluppo di metodologie di calcolo o modelli
teorici. Lo scopo di questa dispensa è quello di fornire in modo semplice e immediato i primi elementi per eseguire
con Mathematica le più comuni operazioni di calcolo, algebra ed analisi elementare. Naturalmente questa introduzione a Mathematica non può prescindere dalla conoscenza della matematica elementare rimanendo, quest’ultima, la condizione necessaria per comprendere nel dettaglio le vere potenzialità del programma.
Questa introduzione a Mathematica è rivolta a lettori colti nelle discipline matematiche ma non necessariamente
addentro ai loro tecnicismi. Il testo e i relativi esempi si possono tranquillamente leggere in autoapprendimento,
possibilmente con un computer su cui implementare Mathematica a un livello di complessità via via crescente. E’
importante ricordare tuttavia che l’approccio puramente introduttivo tenuto in questa sede ha indotto a tralasciare
completamente gli aspetti di Mathematica inerenti in modo specifico la programmazione, aspetti questi ultimi che
costituiscono probabilmente il valore aggiunto del poter operare con un linguaggio simbolico ad alto livello quale
quello di Mathematica.
1. Introduzione
Mathematica è un sistema integrato di calcolo simbolico. Rispetto ad un sistema di calcolo tradizionale Mathematica è concepito per lavorare con espressioni piuttosto che esclusivamente con dati ed elementi numerici. A seguito
di un’elaborazione, un qualsiasi linguaggio di programmazione (C, C++, Java, Pascal, Fortran, ecc.) o un qualsiasi
programma di calcolo (Excel, Matlab) produce un output necessariamente numerico. In generale gli output
numerici sono espressi in notazione esponenziale ossia in una forma che prevede la definizione di al massimo 16
cifre decimali (la mantissa) e una potenza 10 p (la caratteristica) con un esponente p variabile al massimo da -308 a
308. Va da se che lavorando con numeri molto grandi o molto piccoli, razionali ed irrazionali, la notazione esponenziale con mantissa porta forzatamente al dover introdurre delle approssimazioni (la mantissa può disporre al
massimo di 16 cifre). I linguaggi citati e i programmi di calcolo introducono un’approssimazione sul risultato
dovendo lavorare esclusivamente con numeri che in molti casi devono forzatamente essere approssimati per poter
essere rappresentati e gestiti dalla macchina. Tuttavia, programmi di calcolo numerici così conceiti presentano il
vantaggio di essere particolarmente performanti e efficienti nel caso sia richiesta una veloce elaborazione piuttosto
che un’elevato livello di precisione.
Gli algoritmi di Mathematica sono stati concepiti per poter produrre in ogni caso risultati esatti. In particolare a
seguito di un’elaborazione Mathematica produce risultati numerici solo se esprimibili in forma esatta (in termini di
numeri interi) e restituisce risultati ricorrendo ad una notazione simbolica in tutti quei casi in cui la notazione
numerica non permette la definizione esatta del risultato (risultati esprimibili in termini di frazioni, radicali, logaritmi, esponenti, valori di funzioni trascendenti o trigonometriche). Il risultato espresso attraverso simboli è
comunque considerato esatto. Da questo punto di vista la capacità di Mathematica di manipolare espressioni
simboliche offre la possibilità di produrre in ogni caso risultati esatti. Altri programmi in grado di lavorare, al pari
di Mathematica, con espressioni piuttosto che con forme nuneriche sono Derive e Maxima, quest’ultimo scaricabile
liberamente da Internet.
Un secondo aspetto importante da sottolineare è che Mathematica è in grado, se richiesto dall’utente, di fornire
risultati numerici approssimati con un livello di approssimazione piccolo a piacere. In altre parole, in alternativa al
risultato esatto espresso in notazione simbolica, il programma può produrre, se richiesto dall’utente, il risultato di
una qualsiasi elaborazione in termini numerici con una approssimazione piccola a piacere. Da questo punto di vista
Mathematica è in grado di fornire i risultati numerici con un livello di precisione anche superiore a quella restituita
dai linguaggidi programmazione o dai programmi di calcolo citati. D’altra parte i tempi di calcolo richiesti vanno
via via aumentando al al crescere della precisione desiderata e rispetto ai linguaggi e ai programmi di calcolo, a
Introduzione all'uso di Mathematica.nb
5
via via aumentando al al crescere della precisione desiderata e rispetto ai linguaggi e ai programmi di calcolo, a
parità di precisione richiesta, Mathematica risulta certamente meno performante ed efficientenella velocità di
elaborazione.
Altri punti di forza che hanno indiscutibilmente favorito la diffusione di Mathematica all’interno della comunità
scientifica riguardano la versatilità del sistema ovvero la possibilità di essere eseguito su molte piattaforme (PC
IBM compatibili, Macintosh, sistemi UNIX, etc.) e di essere integrato con altri programmi esterni (ad es. in
FORTRAN o in C).
Da quanto detto si capisce come Mathematica rappresenti un ambiente avanzato ideale per lo sviluppo di modelli
analitici in ambito teorico e al contempo per l’analisi, la rappresentazione e la modellistica di dati dove la precisione del calcolo (piuttosto che la velocità) sia una condizione non prescindibile. La disponibilità in rete di pacchetti contenenti funzioni aggiuntive specializzate per i vari ambiti disciplinari (Chimica, Fisica, Ingegneria,
Biologia, etc.) contribuisce a rendere il programma uno strumento dalle enormi potenzialità per qualsiasi ambitodi
ricerca.
2. Nozioni di base sull'uso di Mathematica
2.1 Input e output
L’architettura di Mathematica è articolata in due applicazioni distinte ma collegate tra loro: il Front End e il
Kernel. Il FrontEnd costituisce l'interfaccia con l'utente e si avvale di un programma di elaborazione testi che
gestisce i comandi di Input/Output verso la parte di sistema (il Kernel) che esegue materialmente l'elaborazione. Il
Kernel è essenzialmente un manipolatore di espressioni simboliche in grado di restituire risultati in termini di
simboli, numeri, stringhe, grafici, suoni e animazioni. L'architettura descritta permette di avere il Kernel e FrontEnd su diverse piattaforme con il vantaggio di poter realizzare ambienti Mathematica multiutente, dotati di un
unico Kernel su una macchina particolarmente performante collegato a molti Front End su macchine personali.
L'interfaccia con l'utente è realizzata dal Front End tramite fogli di lavoro Notebook su cui l'utente scrive i comandi
e le stringhe di input da inviare al Kernel e su cui vengono visualizzati i risultati prodotti dall'elaborazione. Il
Notebook è organizzato in celle segnalate da parentesi quadre visibili sulla destra del foglio di lavoro. Ogni cella
può a sua volta essere partita in sottocelle. Celle e sottocelle sono automaticamente generate da Mathematica
scrivendo sul Notebook un qualsiasi comando generico o stringa. Se si vuole che l’Input sia elaborato dal Kernel,
con produzione di un Output, è necessario dare l’invio all’espressione di input scritta utilizzando il comando
Shift+Invio. Mathematica a questo punto elabora istantaneamente l’espressione inviata e restituisce l’Output
risultante. Gli input inviati e gli output restituiti sono rappresentati e progressivamente numerati sul Notebook in
coppie di sottocelle In[n] e Out[n] con n numero progressivo di input inviati e output ricevuti nella sessione di
lavoro. I risultati ottenuti nel corso di una sessione di lavoro sono salvati in un file notebook con estensione .nb. Si
noti che quando un file notebook viene salvato, chiuso e successivamente riaperto, i tags In[n] e Out[n] identificativi delle sottocelle non ricompaiono nel notebook finchè eventualmente l'utente non richieda di valutare di nuovo
le stringhe di input.
2.2 La funzione Help
Esistono molte risorse per intraprendere lo studio di Mathematica. I libri inerenti l’utilizzo del programma nei più
disparati settori della matematica, della fisica o delle diverse discipline scientifiche e tecniche è certamente rilevante. Si veda a tal riguardo i testi e gli articoli disponibili su Internet e in particolare sul sito della casa produttrice
www.wolfram.com. Un risorsa fondamentale è costituita dalla guida in linea del programma, alla quale si può
accedere premendo il tasto F1 o attivando la funzione Help dal menù pricipale. All’interno della guida si può
trovare per intero il libro The Mathematica Book versione 10 di S. Wolfram, all’interno del quale si può facilmente
navigare in base all’argomento a cui si è interessati. Libri simili sono disponibili per tutte le versioni precedenti di
Mathematica , a partire dalla prima nel 1988 a quella più recente (versione 10.0) del 9 luglio 2014.
Introduzione all'uso di Mathematica.nb
6
Mathematica , a partire dalla prima nel 1988 a quella più recente (versione 10.0) del 9 luglio 2014.
Da un punto di vista operativo le ricerche su uno specifico argomento possono essere eseguite in diverse modalità,
tra le altre attivando ricerche generali su uno specifico argomento dal menù generale (HelpØDocumentation Center
con click sulla funzione Search), attivando la ricerca mediante selezione di un espressione o comando nel Notebook e conseguente comando dal menù principale (HelpØFind Selected Function) o ancora digitando su un cella di
input il comando o l'espressione da ricercare preceduto dal simbolo?. L'esempio seguente illustra la ricerca attivata
tramite la terza modalità indicata.
Esempio 2.2.1
Utilizzando l’operatore
? associato alla funzione Help si esegua la ricerca di informazioni inerenti l’operatore
Manipulate.
? Manipulate
Manipulate [expr, {u,umin,umax}]
generates a version of expr with controls added to allow interactive manipulation of the value of u.
manipulate [expr,{u,...},{v...},...]
provides controls to manipulate each of the u, v, ...
Manipulate@Plot@8A Sin@2 Pi a t + bD<, 8t, 0, 6<,
PlotRange → 8− 5, 5<, PlotStyle −> 8Thick, Red<D,
8A, 0, 5<, 8a, 1, 4<, 8b, 0, 10<D
A
4.65
a
2.
b
0.
4
2
1
2
3
4
5
6
−2
−4
à
Introduzione all'uso di Mathematica.nb
Esempio 2.2.2
Sempre utilizzando l’operatore ? si esegua la ricerca di informazioni circa l’espressione ChemicalData.
? ChemicalData
ChemicalData[]”name”,”propery”]
gives the value of the specified property for the chemical “name”.
ChemicalData@"C60", "Properties"D
8AcidityConstant, AcidityConstants, AdjacencyMatrix,
AlternateNames, AtomPositions, AutoignitionPoint,
BeilsteinNumber, BoilingPoint, BondTally, CASNumber,
CHColorStructureDiagram, CHStructureDiagram, CIDNumber,
Codons, ColorStructureDiagram, CombustionHeat,
CompoundFormulaDisplay, CompoundFormulaString,
CriticalPressure, CriticalTemperature, Density,
DensityGramsPerCC, DielectricConstant, DOTHazardClass,
DOTNumbers, EdgeRules, EdgeTypes, EGECNumber,
ElementMassFraction, ElementTally, ElementTypes, EUNumber,
FlashPoint, FlashPointFahrenheit, FormalCharges,
FormattedName, GmelinNumber, HBondAcceptorCount,
HBondDonorCount, HenryLawConstant, HildebrandSolubility,
HildebrandSolubilitySI, InChI, IonEquivalents,
Ions, IonTally, IsoelectricPoint, IsomericSMILES,
IUPACName, LogAcidityConstant, LowerExplosiveLimit,
MDLNumber, MeltingBehavior, MeltingPoint,
Memberships, MolarVolume, MolecularFormulaDisplay,
MolecularFormulaString, MolecularWeight, MoleculePlot,
Name, NFPAFireRating, NFPAHazards, NFPAHealthRating,
NFPALabel, NFPAReactivityRating, NonHydrogenCount,
NonStandardIsotopeCount, NonStandardIsotopeNumbers,
NonStandardIsotopeTally, NSCNumber, OdorThreshold,
OdorType, PartitionCoefficient, pH, Phase, RefractiveIndex,
Resistivity, RotatableBondCount, RTECSClasses,
RTECSNumber, SideChainAcidityConstant, SMILES, Solubility,
SolubilityType, SpaceFillingMoleculePlot, StandardName,
StructureDiagram, SurfaceTension, TautomerCount,
ThermalConductivity, TopologicalPolarSurfaceArea,
UpperExplosiveLimit, VanDerWaalsConstants, VaporDensity,
VaporizationHeat, VaporPressure, VaporPressureTorr,
VertexCoordinates, VertexTypes, Viscosity<
ChemicalData@"C60", "Name"D
buckminsterfullerene
ChemicalData@"C60", "AlternateNames"D
8buckminsterfullerene−C60, fullerene C60,
footballene, soccerballene, HC60−IhL@5,6Dfullerene<
7
Introduzione all'uso di Mathematica.nb
8
ChemicalData@"C60", "MolecularWeight"D
720.642
ChemicalData@"C60", "Density"D
1.65 × 103
ChemicalData@"C60", "StructureDiagram"D
ChemicalData@"C60", "MoleculePlot"D
ChemicalData@"C60", "SpaceFillingMoleculePlot"D
à
Introduzione all'uso di Mathematica.nb
9
3. Calcolo numerico e calcolo simbolico
3.1 Preliminari
Il modo più semplice di lavorare con Mathematica è usarlo come calcolatore in grado di svolgere calcolo numerico
esatto ed approssimato a qualunque grado di precisione richiesto dall’utente. Per seguire le più comuni operazioni
aritmetiche è necessario seguire alcune semplici regole lessicali per evitare errori sulle stringhe di input.
a. le stringhe di input utilizzano caratteri alfa-numerici del codice ASHI;
b. le quattro operazione sono rappresentate dai simboli +, -, *, / . Per la moltiplicazione l’asterico è facoltativo: se
si tralascia l’asterisco i fattori devono essere separati da uno spazio;
c. l’elevamento a potenza è espresso con il simbolo ^ ;
d. il separatore decimale è il punto;
e. le uniche parentesi algebriche sono quelle tonde, sempre bilanciate, eventualmente annidate;
f. le parentesi quadre sono utilizzate per racchiusere gli argomenti delle numerose funzioni predefinite (built-in
functions) presenti nelle librerie di Mathematica. Le espressioni per il calcolo di logaritmi ed esponenziali (Log[
], Exp[ ]), della radice quadrata (Sqrt[ ]), di valori di seni, coseni ed altre espressioni trigonometriche (Sin[
], Cos[ ], Tan[ ], ArcSin[ ], ArcCos[ ], ArcTan[ ], Sinh[ ], Cosh[ ], Tanh[ ]...) sono alcuni
esempi di funzioni libreria predefinite. Si noti che tutti questi elementi vanno scritti con la lettera iniziale in maiuscolo;
g. le parentesi graffe vanno utilizzate principalmente per contenere gli elementi che costituiscono una lista. Il
concetto di lista in Mathematica identifica una collezione ordinata di oggetti (simboli) di natura non necessariamente numerica. Mathematica utilizza liste per definire e manipolare, tra le altre cose, grandezze vettoriali e
matrici;
h. i commenti di testo all'interno del Notebooks vanno posti tra due asterischi (stringa del tipo * commento * ).
Esempio 3.1.1
Sperimentare le caratteristiche di mathematica provando le seguenti stringhe di input.
2 H3 ∗ 4L^ 2 − 64 ê 2
256
Sqrt@256D
16
8 Log@1 ê ED + Log@ED
−7
HLog@ED + Log@10, 10DL ^3
8
4 HCos@Pi ê 4DL^ 2 + Sin@Pi ê 2D
3
ArcSin@0D + ArcCos@1D + ArcTan@0D
0
à
Da un punto di vista operativo, allo scopo di velocizzare le operazioni di scrittura delle stringhe di input, Mathematica dispone di alcuni operatori che permettono di richiamare nella cella attiva Out[n] i contenuti di input o di output
Introduzione all'uso di Mathematica.nb
10
ica dispone di alcuni operatori che permettono di richiamare nella cella attiva
i contenuti di input o di output
presenti in una delle celle precedenti. Le operazioni di richiamo sono eseguite tramite comandi conteneti il simbolo
%.
%
%%
%n
indica l'ultimo output prodotto;
indica il penultimo output prodotto;
indica l'n-esimo output prodotto;
Esempio 3.1.2
Sperimentare l'utilizzo dell'operatore % su una sequenza di operazioni inviate al Kernel con (caso a) lo stesso ordine
con cui sono state scritte sul Notebook e (caso b) con ordine inverso.
Si considerino ad esempio le operazioni 3! e 4! e le si invii al Kernel una ad una seguendo l’ordine con cui sono
state scritte. Si esegua di seguito l’operatore % .
3!
6
4!
24
%
24
Come atteso l' operatore % scritto sulla cella attiva richiama l’ultimo output prodotto.
Si considerino ora le stesse operazioni ma eseguendo l’invio in ordine inverso rispetto all’ordine con cui sono state
scritte (si dia l'invio prima all'espressione scritta nella cella sotto e solo successivamente alla cella sopra):
3!
6
4!
24
in tal caso l’operatore % continua a richiamare la cella scritta per ultima anche se scritta sopra.
%
24
à
3.2 Aritmetica degli interi
Come accennato sopra in Mathematica il calcolo sugli interi è sempre esatto e completo a differenza di quanto
avviene nei linguaggi di programmazione di calcolo numerico che per interi molto grandi passano forzatamente alla
notazione esponenziale con mantissa approssimata. Da questo punto di vista la capacità di Mathematica di effettuare calcoli esatti anche con numeri molto grandi è davvero impressionante. Questo porta spesso ad ottenere
output molto pesanti dal punto di vista della memoria con conseguente possibilità di crash del programma al
momento del salvataggio del Notebook. Si noti che l’eventuale cancellazione di una cella Out[n] tramite selezione
della cella avviene solo visibilmente sul Notebook ma non in termini di contenuto di memoria. Questo significa che
nel corso di una sessione di lavoro Mathematica mantiene sempre in memoria nel Kernel l’intero insieme di Inputi
Introduzione all'uso di Mathematica.nb
11
nel corso di una sessione di lavoro Mathematica mantiene sempre in memoria nel Kernel l’intero insieme di Inputi
inviati e di Output prodotti. In altre parole Mathematica conserva l’informazione del contenuto di tutte le stringhe
numeriche o simboliche elaborate sul Notebook. Con macchime poco performanti è dunque di fondamentale
impotanza (a) evitare di richiedere precisioni troppo elevate nella definizione di dati numerici per evitare di lavorare con stringhe di output troppo pesanti dal punto di vista della memoria e (b) di eseguire spesso l’operazione di
cancellazione memoria nel Kernel. Il modo più semplice per eseguire l’annullamento della memoria nel Kernel è di
attivate dal menù principale la funzione: Evaluation -> Quit Kernel -> Local e confermare l’operazione con quit .
Esempio 3.2.1
Si testi la capacita di Mathematica nel riprodurre istantaneamnete valori numerici estremamente grandi esprimibili
in termini di exponenti con potenza superiore al 1000. Eseguire successivamente l’operazione di cancellazione di
memoria del Kernel.
13^1000;
13^10 000;
13^100 000;
Mathematica è perfettamente in gradi di produrre i risultati richiesti (assenza di errore di overflow) . Per motivi di
spazio (e di memoria...) è stato inserito il simbolo ; alla fine di ogni stringa di input per omettere la visualizzazione dell’output ottenuto. Per eseguire l’operazione di cancellazione memoria del Kernel si attivi dal menù
principale la funzione Evaluation -> Quit Kernel -> Local e si confermi l’operazione con quit .
à
L'aritmetica sugli interi prevede l'uso di un certo numero di operatori che agiscono in modo specifico per
eseguire le più comuni operazioni matematiche. Si noti che in tutti i casi, in analogia al lessico relativo alle funzioni
libreria predefinite, il nome identificativo degli operatori va scritto con la prima lettera in maiuscolo e l'argomento
dell'operatore va sempre inserito tra parentesi quadre. Alcuni operatori di uso comune su sono elencati di seguito.
: produce il quoziente intero della divisione tra due interi n1 e n2;
Mod[n1,n2]
: produce il resto intero della divisione tra gli stessi due interi;
GCD[n1,...,nk]
: produce il Massimo Comun Denominatore (Greatest Common Divosor) degli interi
n1,...nk;
LCM[n1,...,nk]
: produce il Minimo Comun Multiplo (Least Common Multiple) degli interi n1,...nk;
PrimeQ[n]
: produce la risposta in termini di True o False sulla questione inerente se n è un
numero primo;
Prime[n]
: produce l'n-esimo numero primo;
Divisors[n]
: produce l’elenco (stringa) dei divisori dell'intero n;
FactorInteger[n] : produce la scomposizione in fattori primi dell'intero n.
Quotient[n1,n2]
Esempio 3.2.2
Provare le seguenti stringhe di input relative ad alcuni operatori comunemente usati nell'ambito dell'aritmetica dei
numeri interi.
Quotient@64, 12D
5
Introduzione all'uso di Mathematica.nb
12
Mod@64, 12D
4
GCD@64, 12D
4
LCM@64, 12D
192
PrimeQ@121D
False
Prime@4D
7
Divisors@264D
81, 2, 3, 4, 6, 8, 11, 12, 22, 24, 33, 44, 66, 88, 132, 264<
FactorInteger@264D
882, 3<, 83, 1<, 811, 1<<
à
3.3 Aritmetica dei razionali e degli irrazionali
In analisi matematica un numero razionale è un numero ottenibile come rapporto tra due numeri interi a e b con b
diverso da 0. I numeri razionali formano un campo, indicato con il simbolo
, che può essere pensato come
sottocampo del campo dei numeri reali . Numeri irrazionali sono numeri reali non esprimibili in termini di
frazioni. Numeri razionali ed irrazionali sono sempre esprimibili in forma approssimata utilizzando le forme
decimali. I linguaggi di programmazione e i programmi di calcolo utilizzano la notazione esponziale con mantissa
approssimata quando si trovano a dover gestire e rappresentare espressioni numeriche razionali e irrazionali.
Come già accennato, il programma Mathematica è pensato per lavorare con espressioni simboliche piuttosto che
numeri e questa capacità di eseguire manipolazioni su espressioni non necessariamente numeriche è in realtà la
chiave per poter eseguire calcoli esatti non solo con numeri interi ma anche con numeri razionali ed irrazionali. In
particolare se il risultato di un calcolo è un numero razionale non esprimibile in forma numerica esatta Mathematica, a differenza di un programma in grado di gestire solo calcolo numerico, utilizza una notazione simbolica (con
il simbolo di frazione) piuttosto che una notazione numerica approssimata e questo gli permette di non dover
necessariamente introdurre approssimazioni sulla valutazione del risultato. In modo analogo se a seguito di un’elabotazione, Mathematica si trova a dover restituire risultati caratterizzati dalla presenza di espressioni numeriche
irrazionali (espressioni contenenti radicali, esponenziali e logaritmi o ancora funzioni trigonometriche e trascendenti valutate su argomenti razionali o irrazionali) allora i suoi algoritmi prevedono output espressi in linguaggio
simbolico (utilizzando i simboli
a , , Log[a], π) piuttosto che numerico approssimato e questo consente di
considerare il risultato ancora una volta espresso in forma esatta. Gli esempi che seguono illustrano bene come
Mathematica fornisca nei diversi casi sempre soluzioni esatte.
Introduzione all'uso di Mathematica.nb
13
Esempio 3.3.1
Si dimostri che il calcolo eseguito con Mathematica nel caso di espressioni caratterizzate dalla presenza di (a)
razionali; (b) radicali; (c) logaritmi; (d) numeri irrazionali; (e) forme trigonometriche produce soluzioni espresse
quando possibile in forma numerica esatta o in alternativa in forma simbolica (comunuqe esatta).
Si considerino ad esempio le seguenti operazioni:
1+1ê3
4
3
2 Sqrt@2D
2
2
E + Pi
+π
Cos@Pi ê 3D + Sin@Pi ê 3D
1
2
+
3
2
4 Log@ED
4
Cos@Pi ê 2D + Sin@Pi ê 2D
1
Le prime quattro operazioni sono caratterizzate da risultati non esprimibili tramite interi ossia risultati esprimibili
solo in termini di numeri razionali o irrazionali. Mathematica in questi casi restituisce output contenenti forme
simboliche in quanto non in grado di riprodurre i risultati numerici in forma esatta. Risultati simbolici sono risultati
esatti. Le ultime due operazioni, pur contenendo nell’input numeri irrazionali, producono risultati esprimibili in
termini di interi e dunque gli algoritmi di Mathematica forniscono le soluzioni in forma numerica esatta senza
dover ricorrere all’uso di simboli. In tutti i casi i risultati forniti dal programma sono risultati esatti.
à
3.4 Calcolo esatto e approssimato
In Mathematica risultati caratterizzati da espressioni contenenti numeri razionali (frazioni) e irrazionali (radicali,
logaritmi, valori di funzioni algebriche o trascendenti di argomenti razionali) sono sempre matematicamente esatti
perchè espressi o in forma numerica esatta (quando possibile) o in forma simbolica (in tutti gli altri casi). Tuttavia,
se richiesto dall’utente, Mathematica è in grado di gestire espressioni numeriche anche come un progranmma di
calcolo numerico e in tal caso fornire i risultati in forma numerica esatta (quando possibile) o in forma numerica
approssimata introducendo la notazione decimale. A differenza però dei linguaggi di programmazione o dei
migliori programmi di calcolo, veloci nell’elaborazione ma con precisione limitata, Mathematica non presenta
limiti di precisione e l’approssimazione sui decimali nella valutazione di un risultato può essere resa piccola a
piacere. L’elavata precisione è però pagata in termini di tempi di elaborazione e da questo punto di vista Mathematica non può certo competere con i programmi che lavorano esclusivamente con dat ed elementi numerici.
La valutazione dei risultati in termini decimali viene fornita (con un numero di decimali grande a piacere) solo se
Introduzione all'uso di Mathematica.nb
14
La valutazione dei risultati in termini decimali viene fornita (con un numero di decimali grande a piacere) solo se
espressamente richiesta dall’utente. In particolare la richiesta può essere eseguita o introducendo un input espresso
in notazione decimale o utilizzando l’operatore N[ ] che permette la valutazione di un’espressione
espr con
una precisione eventualmente definita dall’operatore. Ilsimbolo espr indica un’espressione contenente numeri
razionali non esprimibili in forma esatta o numeri irrazionali.
: produce l’approssimazione con 5 decimali dopo
la virgola di un’espressione espr non esprimibile
in forma esatta.
N[espr,m]
: produce l’approssimazione con un numero m di cifre
decimali dopo la virgola.di un’espressione espr
non esprimibile in forma esatta.
block[{$MaxExtraPrecision=mmax},N[espr,m]] : produce l’approssimazione con un numero m di cifre
decimali dopo la virgola.di un’espressione espr
dopo che essa sia stata espressa con un numero
nmax di cifre decimali dopo la virgola.
N[espr]
Esempio 3.4.1
Si verifiche che i numeri razionali in Mathematica sono espressi in forma numerica esatta (quando possibile) o in
forma simbolica (comunque esatta) in tutti gli altri casi.
8ê4
2
10 ê 4
5
2
11 ê 4
11
4
La prima frazione è esprimibile attraverso un intero ed in effetti gli algoritmi di Mathematica restituiscono un
risultato espresso in forma numerica esatta. Negli altri casi le frazioni non sono riconducibili a numeri interi e
Mathematica restituisce una rappresentazione dei numeri utilizzando la forma simbolica (frazione ridotta ai minimi
termini). In tutti i casi i risultati forniti sono espressi in forma esatta.
à
Esempio 3.4.2
Si verifichi che Mathematica, nel caso le frazioni non siano esprimibili in forma numerica esatta, può fornire (se
richiesto dall'utente) anche una rapresentazione dei numeri in forma numerica approssimata con un numero di
decimali grande a piacere.
L' utente può richiedere la notazione decimale direttamente inserendo la notazione decimale nelle espressioni di
input o tramite l'operatore N.
8 ê 4.
2.
Introduzione all'uso di Mathematica.nb
15
10 ê 4.
2.5
11 ê 3.
3.66667
N@8 ê 4, 15D
2.00000000000000
N@10 ê 4, 15D
2.50000000000000
N@11 ê 3, 15D
3.66666666666667
à
Esempio 3.4.3
Si verifichi che la notazione con cui è espresso il risultato di una determinata elaborazione è strettamente correlato
alla notazione delle forme numeriche di input.
5ê2−5ê2
0
5 ê 2 − 2.5
0.
2.5 − 2.5
0.
I tre casi considerati dimostrano come Mathematica elabora in modo molto diverso i numeri espressi in forma
esatta e quelli espressi in forma approssimata. In tutti i casi il risultato è lo stesso ma la notazione utilizzata da
Mathematica per esprimerlo è diversa. La differenza tra due numeri uguali, entrambi espressi in forma esatta, porta
ad un risultato espresso in forma esatta. La differenza tra due numeri uguali, uno solo dei quali espresso in forma
approssimata o entrambi espressi in forma approssimata, porta ad un risultato espresso in forma approssimata.
Nella scelta della notazione è bene tener presente che, in Mathematica, la valutazione di espressioni complesse
contenenti numeri in forma approssimata richiede un tempo tipicamente inferiore rispetto alle stesse valutazioni
eseguite in forma esatta. Tenere a mente questa differenza può portare pertanto a realizzare modelli con tempi di
esecuzione ottimizzati.
à
Esempio 3.4.4
Si verifichi che nel caso di (a) numeri etremamente grandi o estremamente piccoli; (b) radicali; (c) valori espressi
tramite funzioni trigonometriche calcolate su argomenti razionali; Mathematica, se esplicitamente richiesto dall’utente, è in grado di fornisce risultati esprimendoli in forma numerica esponenziale con mantissa approssimata con
un numero di cifre dopo la virgola grande a piacere.
Introduzione all'uso di Mathematica.nb
16
a.
3^H− 80L
1
147 808 829 414 345 923 316 083 210 206 383 297 601
N@3^H− 80LD
6.7655 × 10−39
N@3^H− 80L, 10D
6.765495701 × 10−39
N@3^H− 80L, 100D
6.76549570118537666651396927813051162547608550347538624611248
3390156825201895989694421015932752895595 × 10−39
b.
Sqrt@3D
3
N@Sqrt@3DD
1.73205
N@Sqrt@3D, 10D
1.732050808
N@Sqrt@3D, 100D
1.73205080756887729352744634150587236694280525381038062805580
6979451933016908800037081146186757248576
c.
Sin@Pi ê 3D + Cos@Pi ê 3D
1
2
+
3
2
N@Sin@Pi ê 3D + Cos@Pi ê 3DD
1.36603
N@Sin@Pi ê 3D + Cos@Pi ê 3D, 100D
1.36602540378443864676372317075293618347140262690519031402790
3489725966508454400018540573093378624288
à
Introduzione all'uso di Mathematica.nb
17
Esempio 3.4.5
Si sperimentimo le modalità con cui l'operatore block[{$MaxExtraPrecision = mmax}, N[espr, m]]
opera su un’espressione numerica estremamente piccola.
Cos@1D^2 + Sin@1D^2 − Sqrt@1 − Exp@−1000DD
−
1−
1
1000
+ Cos@1D2 + Sin@1D2
N@Cos@1D^2 + Sin@1D^2 − Sqrt@1 − Exp@−1000DDD
−1.11022 × 10−16
N@Cos@1D^2 + Sin@1D^2 − Sqrt@1 − Exp@−1000DD, 10D
— N::meprec :
Internal precision limit $MaxExtraPrecision = 50.` reached while
evaluating -
1-
1
‰
1000
+ Cos@1D2 + Sin@1D2 . à
0. × 10−60
N@Cos@1D^2 + Sin@1D^2 − Sqrt@1 − Exp@−1000DD, 100D
— N::meprec :
Internal precision limit $MaxExtraPrecision = 50.` reached while
evaluating 0. × 10
1-
1
‰
1000
+ Cos@1D2 + Sin@1D2 . à
−150
N@Cos@1D^2 + Sin@1D^2 − Sqrt@1 − Exp@−1000DD, 500D
— N::meprec :
Internal precision limit $MaxExtraPrecision = 50.` reached while
evaluating -
1-
1
‰
1000
+ Cos@1D2 + Sin@1D2 . à
2.53797944877472838264590473978716845965279964144641868091619
6922705270271487409587839831084523271433931833553415533 × 10−435
Block@8$MaxExtraPrecision = 500<,
N@Cos@1D^ 2 + Sin@1D^ 2 − Sqrt@1 − Exp@− 1000DD, 20DD
2.5379794487747283826 × 10−435
à
Introduzione all'uso di Mathematica.nb
18
3.5 Algebra
Per le sue caratteristiche Mathematica trova il suo più naturale impiego nell’ambito dell’elaborazione e della
manipolazione di espressioni algebriche. Gli algoritmi di cui è dotato permettono di trasformare una espressione
algebrica di input in un’espressione equivalente di output, sepre rimanendo nell’ambito del linguaggio simbolico. In
particolare Mathematica è in grado di sviluppare, fattorizzare e semplificare polinomi estremamente complessi,
calcolare le soluzioni di equazioni e sistemi di equazioni polinomiali e più in generale manipolare espressioni
algebriche estremamente complesse. Di seguito sono riportati gli operatori attraverso cui eseguire le più comuni
operazioni di tipo algebrico su un polinomio (indicato con il simbolo px) o più polinomi (indicati con pxi,
i=1,...,n).
Expand[px]
Factor[px]
Simplify[px]
FullSimplify[px]
Together[px]
Apart[px]
:
:
:
:
:
:
produce lo sviluppo di px ;
produce la fattorizzazione di px;
produce la semplificazione di px;
produce la semplificazione di px ad un livello superiore;
produce la composizione di un px a partire dalla somma di frazioni;
produce la scomposizione in frazioni di px;
Gli esempi che seguono illustrano l’utilizzo degli operatori visti.
Esempio 3.5.1
Si consideri la forma algebrica px = Hab + b + cL3 - 1 e si eseguano le più comuni operazioni algebriche di scomposizione in monomi e semplificazione.
Le operazioni algebriche richieste sono pressochè immediate:
Ha b + b + cL ^3 − 1
−1 + Hb + a b + cL3
Expand@Ha b + b + cL ^3 − 1D
−1 + b3 + 3 a b3 + 3 a2 b3 + a3 b3 +
3 b2 c + 6 a b2 c + 3 a2 b2 c + 3 b c2 + 3 a b c2 + c3
SimplifyA−1 + b3 + 3 a b3 + 3 a2 b3 + a3 b3 +
3 b2 c + 6 a b2 c + 3 a2 b2 c + 3 b c2 + 3 a b c2 + c3 E
−1 + H1 + aL3 b3 + 3 H1 + aL2 b2 c + 3 H1 + aL b c2 + c3
FullSimplifyA−1 + b3 + 3 a b3 + 3 a2 b3 +
a3 b3 + 3 b2 c + 6 a b2 c + 3 a2 b2 c + 3 b c2 + 3 a b c2 + c3 E
−1 + Hb + a b + cL3
Si noti che già con un’espressione semplice come quella vista è stato necessario utilizzare il comando FullSimplify per ottenere con successo la semplificazione alla forma iniziale.
à
Introduzione all'uso di Mathematica.nb
19
Esempio 3.5.2
2
Si consideri la forma algebrica px = Ix2 - 1M Ix2 - 2M Ix2 - 4M
3
e si eseguano le più comuni operazioni algebriche
di scomposizione in monomi e fattorizzazione. Si calcoli l’espressione algebrica ottenuta per x=a e se ne esegua
l’elevamento a potenza 3/2.
Hx^2 − 1L Hx^2 − 2L^2 Hx ^2 − 4L ^3
I−4 + x2 M I−2 + x2 M I−1 + x2 M
3
2
Le operazioni di scomposizione in monomi e fattorizzazione possono essere eseguite con i comandi Expand
e
Factor:
Expand@Hx^2 − 1L Hx^2 − 2L^2 Hx ^2 − 4L ^3D
256 − 704 x2 + 752 x4 − 404 x6 + 116 x8 − 17 x10 + x12
FactorA256 − 704 x2 + 752 x4 − 404 x6 + 116 x8 − 17 x10 + x12 E
H−2 + xL3 H−1 + xL H1 + xL H2 + xL3 I−2 + x2 M
2
E’ possibile a questo punto assegnare il valore a alla variabile x e successivamente calcolare il valore assunto da px
in a semplicemente richiamando il polinomio stesso:
x=a
a
FactorA256 − 704 x2 + 752 x4 − 404 x6 + 116 x8 − 17 x10 + x12 E
H−2 + aL3 H−1 + aL H1 + aL H2 + aL3 I−2 + a2 M
2
Si noti che lo stesso risultato avrebbe potuto essere raggiunto utilizzando anche l’operatore
% , ossia richiamando
la stringa che identifica il polinomio:
%%%
H−2 + aL3 H−1 + aL H1 + aL H2 + aL3 I−2 + a2 M
2
L’elevamento a potenza 3/2 dell’espressione ottenuta è immediata:
%^H3 ê 2L
JH−2 + aL3 H−1 + aL H1 + aL H2 + aL3 I−2 + a2 M N
2 3ê2
à
Esempio 3.5.3
2 ax
Si consideri la forma algebrica px = Ha−3L Ha+5L e la si elevi alla potenza 10. Si eseguano le stesse operazioni dopo
aver posto (a) a=5 e (b) a=3.
Le operazioni che seguono sono immediate se si assegna al polinomio la variabile espr:
2 ax ê HHa − 3L Ha + 5LL
2 ax
H−3 + aL H5 + aL
Introduzione all'uso di Mathematica.nb
20
expr = 2 a ê HHa − 3L Ha + 5LL
2a
H−3 + aL H5 + aL
expr^10
1024 a10
H−3 + aL10 H5 + aL10
a=5
5
expr^10
1
1024
a=3
3
expr^10
— Power::infy : Infinite expression
ComplexInfinity
1
0
encountered. à
à
4 Equazioni e sistemi di equazioni lineari
4.1 Risoluzione di equazioni in forma esatta
Mathematica è in grado di risolvere equazioni di grado uguale o superiore al primo o utilizzando algoritmi diversi a
seconda che si cerchino soluzioni esatte o approssimate. Trovare le soluzioni esatte di una equazione significa, con
passaggi algebrici opportuni, determinare il valore esatto delle sue radici (è questo il caso, ad es. delle radici fornite
dalla formula per la risoluzione delle equazioni di secondo grado). Risolvere un’equazione con approssimazione
significa determinare, con metodi dell’analisi numerica (ad es. mediante algoritmi iterativi) una soluzione approssimata o tutte le soluzioni approssimate dell’equazione. La risoluzione esatta delle equazioni è eseguita mediante gli
operatori Solve e NSolve. In caso non fosse possibile trovare le soluzioni esatte di un’equazione gli operatori
Solve e NSolve non producono risultato. Solve e NSolve si differenziano unicamente per come rappresen-
tano le soluzioni calcolate in modo esatto. L’operatore Solve produce le soluzioni esatte attraverso, quando
possibile, espressioni numeriche esatte (ossia con numeri interi) o in alternativa tramite linguaggio simbolico.
L’operatore NSolve restituisce invece le soluzioni esatte utilizzando la notazione decimale e dunque introducendo
un’approssimazione sulla rappresentazione dei numeri. Si noti che in entrambi i casi il segno di uguaglainza va
indicato, come in C e Java, raddoppiando l’usuale segno algebrico = . Ovviamente la scelta della variabile è
indifferente.
Introduzione all'uso di Mathematica.nb
21
: produce le soluzioni esatte (reali o complesse) di un’equazione di grado uguale
o superiore al primo e ne fornisce la rappresentazione in notazione esatta;
NSolve[A[x]==B[x], x] : produce le soluzioni esatte (reali o complesse) di un’equazione di grado uguale
o superiore al primo e ne fornisce la rappresentazione in notazione (decimale)
approssimata.
Solve[A[x]==B[x], x]
Esempio 4.1.1
Si calcolino le radici dell'equazione di secondo grado: x2 - 4 = 0 .
La soluzione dell'equazione porta a due radici reali e distinte. Utilizzando Solve e NSolve le due radici possono
essere espresse , rispettivamente, in notazione simbolica esatta o in notazione numerica approssimata.
x^2 − 4 == 0
−4 + x2 0
Solve@x^2 − 4 == 0, xD
88x → −2<, 8x → 2<<
NSolve@x^2 − 4 0. xD
88x → −2.<, 8x → 2.<<
à
Esempio 4.1.2
Si calcolino le radici dell'equazione di terzo grado: x3 + x2 + 1 = 0 .
In questo caso si tratta di una radice reale e due radici complesse coniugate.
x^3 + x^2 + 1 == 0
1 + x2 + x3 0
Solve@x^3 + x^2 + 1 0, xD
::x →
1
−1 −
3
:x → −
1
+
3
3×
1
3
−
29 − 3
1
6
J1 + +
22ê3
1
6
J1 − 1
2
3
J29 − 3
93 N
3N
1
2
1
2
93
3N
1−
−
1ê3
2
1ê3
1ê3
J29 − 3
93 N
>,
1ê3
J29 − 3
93 N
+
>, :x →
1ê3
J29 − 3
93 N
1+
+
3×
22ê3
J29 − 3
3
1ê3
93 N
>>
Introduzione all'uso di Mathematica.nb
22
NSolve@x^3 + x^2 + 1 0, xD
88x → −1.46557<, 8x → 0.232786 − 0.792552 <,
8x → 0.232786 + 0.792552 <<
à
Esempio 4.1.3
Si determinino le radici dell'equazione ‰2 x - 3 ‰x + 1 = 0 . Si tratta di un'equazione di secondo grado in x che
può essere calcolata esattamente. Il calcolo porta a due radici reali e distinte.
Exp@2 xD − 3 Exp@xD + 1 0
1 − 3 x + 2 x 0
Solve@Exp@2 xD − 3 Exp@xD + 1 0, xD
— Solve::ifun :
Inverse functions are being used by Solve, so some solutions may not
be found; use Reduce for complete solution information. à
::x → LogB
1
2
I3 −
5 MF>, :x → LogB
1
2
I3 +
5 MF>>
NSolve@Exp@2 xD − 3 Exp@xD + 1 0, xD
— NSolve::ifun :
Inverse functions are being used by NSolve, so some solutions may not
be found; use Reduce for complete solution information. à
88x → −0.962424<, 8x → 0.962424<<
Mathematica produce tuttavia un messaggio di testo nel quale viene suggerito di utilizzare il comando Reduce per
trovare altre possibili soluzioni.
Reduce@Exp@2 xD − 3 Exp@xD + 1 0, xD
C@1D ∈ Integers && Ix 2 π C@1D − Log@2D + LogA3 −
x 2 π C@1D − Log@2D + LogA3 +
5 EM
5 E »»
In effetti il comando Reduce produce l'insieme delle radici complesse cercate.
à
Introduzione all'uso di Mathematica.nb
23
Esempio 4.1.4
Si determinino le radici dell'equazione 1 - 2 x2 + ax3 = 0.
Si tratta di un'equazione simbolica di terzo grado di cui Mathematica è in grado di calcolare le radici (una radice
reale e due complesse coniugate).
a x^3 − 2 x^2 + 1 0
1 − 2 x2 + a x3 0
Solve@a x^3 − 2 x^2 + 1 0, xD
::x →
1
2
3
a
4 × 21ê3
+
+
1ê3
a 16 − 27 a2 + 3
−32 a2 + 27 a4
3
1ê3
16 − 27 a2 + 3
− 32 a2 + 27 a4
3
>,
21ê3 a
:x →
2
2 × 21ê3 J1 + −
3N
−
1ê3
3a
3 a 16 − 27 a2 + 3
J1 − −32 a2 + 27 a4
3
1ê3
3 N 16 − 27 a2 + 3
−32 a2 + 27 a4
3
>,
6 × 21ê3 a
:x →
2
2 × 21ê3 J1 − −
3a
J1 + 3N
−
1ê3
3 a 16 − 27
a2
+3
3 N 16 − 27 a2 + 3
−32
3
a2
+ 27
a4
1ê3
3
6 × 21ê3 a
−32 a2 + 27 a4
>>
Introduzione all'uso di Mathematica.nb
24
NSolve@a x^3 − 2 x^2 + 1 0, xD
::x → 0.333333
2.
a
5.03968
+
+
1ê3
a 16. − 27.
a2
+ 5.19615
− 32.
a2
+ 27.
a4
1ê3
0.793701 16. − 27. a2 + 5.19615
−32. a2 + 27. a4
>,
a
:x →
0.666667
a
a 16. − 27. a2 + 5.19615
− 32. a2 + 27. a4
H0.132283 − 0.229122 L
1ê3
16. − 27. a2 + 5.19615
:x →
0.666667
1
a
−
1ê3
a
1
0.839947 + 1.45483 −
a
−32. a2 + 27. a4
>,
0.839947 − 1.45483 −
−
1ê3
a 16. − 27.
a2
+ 5.19615
−32.
a2
+ 27.
a4
H0.132283 + 0.229122 L
1ê3
16. − 27. a2 + 5.19615
−32. a2 + 27. a4
>>
In entrambi i casi le soluzioni fornite da Mathematica appaiono estremamente complesse non essendo il programma in grado di produrre ulteriori semplificazioni delle soluzioni in assenza di una migliore identificazione del
simbolo a.
Con a=1, per esempio, le soluzioni, tutte reali, assumono forma semplificata.
Solve@x^3 − 2 x^2 + 1 0, xD
1
1
:8x → 1<, :x →
I1 − 5 M>, :x →
I1 +
2
2
5 M>>
NSolve@x^3 − 2 x^2 + 1 0, xD
88x → −0.618034<, 8x → 1.<, 8x → 1.61803<<
à
Introduzione all'uso di Mathematica.nb
25
Esempio 4.1.5
Verificare che nel caso dell’equazione x5 - x3 + 1 = 0 Mathematica è in grado di produrre il calcolo delle radici
esatte ma non è in grado di rappresentarne le radici in forma esatta.
x^5 − x^3 + 1 == 0
1 − x3 + x5 0
Solve@x^5 − x^3 + 1 == 0, xD
99x → RootA1 − 13 + 15 &, 1E=,
9x → RootA1 − 13 + 15 &, 2E=, 9x → RootA1 − 13 + 15 &, 3E=,
9x → RootA1 − 13 + 15 &, 4E=, 9x → RootA1 − 13 + 15 &, 5E==
Le espressioni sopra evidenziano l'impossibilità di ottenere da Mathematica radici esatte dell'equazione espresse in
forma esatta. Il calcolo delle radici in forma decimale approssimata con l'operatore NSolve fornisce invece il
risultato richiesto. Si tratta di una soluzione reale e quattro soluzioni complesse, a due a due complesse coniugate.
NSolve@x^5 − x^3 + 1 == 0, xD
88x → −1.23651<, 8x → − 0.340795 − 0.785423 <,
8x → −0.340795 + 0.785423 <,
8x → 0.959048 − 0.428366 <, 8x → 0.959048 + 0.428366 <<
à
4.2 Risoluzione di equazioni in forma approssimata
Quando per un'equazione non è possibile ottenere soluzioni esatte, Mathematica fornisce soluzioni calcolate in
forma approssimata con l’operatore FindRoot. Il comando trova soluzioni approssimate dell'equazione utilizzando
algoritmi iterativi calcolati a partire da un determinato valore iniziale x0 fornito dall'utente. Essendo il valore di
convergenza dell'algoritmo (valore approssimato della soluzione) dipendente dal valore iniziale del calcolo, la
soluzione trovata necessita di una verifica eseguita a posteriori per via grafica. L’operatore Plot permette di
rappresentare graficamente le espressioni A(x) e B(x) che compongono l’equazione da risolvere per evidenziare
l’effettiva coincidenza delle radici calcolate con i punti di intersezione dei due grafici. L’esempio 4.3.1 illustra bene
il metodo.
FindRoot[A[x]==B[x],x,x0]
Plot[{A[x],B[x]},{x,a,b}]
: produce le soluzioni approssimate di un’equazione con soluzioni
non calcolabili analiticamente;
: produce la rappresentazione grafica delle espressioni A[x] e B[x]
nell'internallo [a,b] della variabile indipendente x.
Esempio 4.2.1
Si determinino le soluzioni dell’equazione sen HxL =
x
2
L’espressione è un'equazione trascendente il cui calcolo delle radici non è fattibile in termini analitici. L'operatore
FindRoot permette di calcolarne le soluzioni in forma approssimata.
Sin@xD x ê 2
x
Sin@xD 2
Introduzione all'uso di Mathematica.nb
26
Il calcolo delle radici in forma approssimata è sensibilmente dipendente dal punto iniziale x0 da cui gli l’algoritmi
di Mathematica intraprendono il calcolo iterativo. Per valori di x0 diversi il calcolo iterativo delle radici porta a
soluzioni diverse, come si evince dai seguneti casi.
FindRoot@Sin@xD x ê 2, 8x, 1.5<D
8x → 1.89549<
FindRoot@Sin@xD x ê 2, 8x, 1.<D
8x → 0.<
FindRoot@Sin@xD x ê 2, 8x, −1.<D
8x → 0.<
FindRoot@Sin@xD x ê 2, 8x, −1.5<D
8x → −1.89549<
A partire da diversi valori di x0 il calcolo iterativo produce soluzioni numeriche. La rappresentazione grafica delle
espressioni A[x] e B[x] che compongolo l’equazione permette la verifica a posteriori dell’effettiva correttezza delle
radici calcolate (punti di intersezione dei grafici A[x] e B[x]).
Plot@8Sin@xD, x ê 2<, 8x, −2 Pi, 2 Pi<,
PlotStyle −> 8Thick, Red<, PlotStyle −> 8Thick, Blue<D
3
2
1
−6
−4
−2
2
4
6
−1
−2
−3
In effetti il grafico prodotto conferma che le radici ({x→-1.89549},{x→0},{x→-1.89549}) calcolate dagli
algoritmi di Mathematica, a partire da diversi valori di x0, cpoincidono con i punti di intersezione delle curve.
à
Introduzione all'uso di Mathematica.nb
27
Esempio 4.2.2
Si calcolino in forma approssimata le radici dell'equazione tg HxL = x.
Tan@xD x
Tan@xD x
FindRoot@Tan@xD x, 8x, Pi ê 4<D
9x → 2.03897 × 10−8 =
FindRoot@Tan@xD x, 8x, Pi ê 12<D
9x → 1.48945 × 10−8 =
FindRoot@Tan@xD x, 8x, H5 ê 4L Pi<D
8x → 4.49341<
FindRoot@Tan@xD x, 8x, H18 ê 12L Pi<D
8x → 4.71239<
FindRoot@Tan@xD x, 8x, H5 ê 3L Pi<D
8x → 7.72525<
Le radici calcolate con metodi iterativi appaiono di difficile interpretazione in riferimento al valore del parametro
x0 scelto. In questa situazione la verifica grafica è essenziale per comprendere la natura delle radici e dell'equazione data.
Plot@8Tan@xD, x<, 8x, −4 Pi, 4 Pi<,
PlotStyle −> 8Thick, Red<, PlotStyle −> 8Thick, Blue<D
20
10
−10
−5
5
10
− 10
− 20
Il grafico ottenuto è esplicativo delle radici ({x→-1.89549},{x→0},{x→-1.89549}) calcolate dagli algoritmi di
Mathematica, a partire da diversi valori di x0.
à
Introduzione all'uso di Mathematica.nb
28
4.3 Sistemi di equazioni (cenni)
In modo analogo a quanto fatto con le equazioni ma con comprensibile cambio di sintassi Mathematica è in grado
di risolvere sistemi di equazioni lineari e (talvolta) non lineari. Gli operatori Solve e NSolve permettono di
ottenere le soluzioni esatte del sistema rappresentate in forma esatta e decimale approssimata, rispettivamente. Si
noti come siano state utilizzate le liste { } per indicare la presenza di più equazioni del tipo A1 ( x1 ,
... xn ) = B1 (x1 ,
... xn ) , ... , An (x1 , ... xn ) = Bn (x1 , ... xn ) da risolvere simultaneamente.
Solve[{A1[x1,...,xn]==B1[x1,...,xn],...,An[x1,...,xn]==Bn[x1,...,xn]},{x1,...,xn}]
produce le soluzioni esatte (reali o complesse) di un sistema di equazioni e ne fornisce la rappresentazione in
notazione esatta;
NSolve[{A1[x1,...,xn]==B1[x1,...,xn],...,An[x1,...,xn]==Bn[x1,...,xn]},{x1,...,xn}]
produce le soluzioni esatte (reali o complesse) di un sistema di equazioni e ne fornisce la rappresentazione in
notazione (decimale) approssimata;
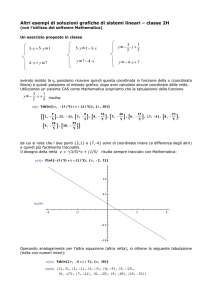
Esempio 4.3.1
Si verifichi che la soluzione esatta dei seguenti sistemi è immediata.
8x ê 2 + y ê 3 3 a, H1 ê 3L x − y 1<
x y
x
: + 3 a,
− y 1>
2 3
3
Solve@8x ê 2 + y ê 3 3 a, H1 ê 3L x − y 1<, 8x, y<D
6
9
18 a
::x →
H1 + 9 aL, y → −
+
>>
11
11
11
NSolve@8x ê 2 + y ê 3 3 a, H1 ê 3L x − y 1<, 8x, y<D
88x → 0.545455 + 4.90909 a, y → − 0.818182 + 1.63636 a<<
Esempio 4.3.2
Come l’esempio 4.3.1 ma con un sistema più complicato da risolvere e spingendo l’approssimazione numerica a 20.
8x^2 ê 2 + y^ 3 ê 3 3, H1 ê 3L x − y 1<
x2 y3
x
:
+
3,
− y 1>
2
3
3
Introduzione all'uso di Mathematica.nb
29
Solve@8x^2 ê 2 + y^ 3 ê 3 3, H1 ê 3L x − y 1<, 8x, y<D
::x →
3
−7 +
2
1
y→
−9 +
2
:x →
3
15
1
J3
J− 29 + 2 15
1
J3
−14 −
4
J−29 + 2 1
J3
J−29 + 2 15 J1 + 4
:x →
3
J−29 + 2 −14 −
4
71 NN
71 NN
71 N
3N
71 NN
1ê3
−
1ê3
+ 32ê3 J−29 + 2 71 N
1
4
−
1ê3
J 3 J−29 + 2 3 31ê6 J−29 + 2 15 J1 − 4 J 3 J−29 + 2 3N
71 NN
1ê3
−
1ê3
1
4
J− 29 + 2 32ê3 J1 − 71 NN
71 N
15 35ê6
− 32ê3 J−29 + 2 15
1
1
1ê3
71 N
15
3 31ê6 J−29 + 2 1
J3
71 NN
1ê3
+ 32ê3 J− 29 + 2 +
1ê3
71 N
71 N
1ê3
− 32ê3 J−29 + 2 1ê3
, y→−
9
−
2
71 N
71 N
>,
+
3 N J− 29 + 2 J− 29 + 2 ,
1ê3
15 35ê6
32ê3 J1 + 1ê3
71 N
1ê3
>,
−
1ê3
1ê3
, y→−
3 N J− 29 + 2 9
−
2
71 N
1ê3
>>
NSolve@8x^2 ê 2 + y^ 3 ê 3 3, H1 ê 3L x − y 1<, 8x, y<D
88x → −30.3156, y → − 11.1052<,
8x → 2.45033, y → − 0.183224<, 8x → −3.63474, y → −2.21158<<
NSolve@8x^2 ê 2 + y^ 3 ê 3 3, H1 ê 3L x − y 1<, 8x, y<, 20D
88x → −30.315582348461309331, y → − 11.105194116153769777<,
8x → 2.4503266536476877954, y → − 0.18322444878410406819<,
8x → −3.634744305186378465, y → −2.2115814350621261549<<
à
Introduzione all'uso di Mathematica.nb
30
5 Funzioni reali
5.1 Premessa: l'uguaglianza
In Mathematica esistono tre tipi di uguaglianza e ciascuna di esse svolge un ruolo ben preciso: la definizione, la
definizione differita, l'uguaglianza in una equazione.
In particolare:
la definizione semplice si ottiene con il simbolo = . L’espressione alla sinistra del simbolo = diventa immediatamente uguale all’espressione che compare alla sua destra e l’identità asserita è fissa nel senso che ogni qualvolta
venga richiamata l’espressione di sinistra Mathematica automaticamente e istantaneamente esegue l’associazione
con l’espressione a destra.
La definizione differita si ottiene con il simbolo := . Il suo significato è profondamente diverso dalla definizione
semplice. Dopo aver eseguito la definizione differita ad ogni richiamo successivo dell’espressione di sinistra
Mathematica non restituisce immediatamente ed automaticamente l’espressione di destra ma la valuta di volta in
volta tenendo conto di eventuali aggiornamenti eseguiti nel frattempo in riferimento alle espressioni o alle variabili
presenti nell’identificazione.
L’uguaglianza in un’equazione si ottiene con il simbolo == . Si tratta dell’operatore logico utilizzato per scrivere e
gestire equazioni o sistemi di equazioni.
In particolare le operazioni di definizione permettono di assegnare nomi a espressioni matematiche (ad es. a
funzioni) o valori a variabili. Le definizioni su espressioni possono essere successivamente annullate tramite
l’operatore Clear. Le definizioni su variabili possono essere annullate utilizzando il simbolo =. .
Gli esempi che seguono sono importanti per comprendere il significato dei tre tipi di uguaglianza e i loro rispettivi
ruoli.
Esempio 5.1.1
Si verifichino le modalità di esecuzione, richiamo ed annullamento dell’operazione di definizione semplice.
L’assegnazione di un nome ad un’espressione (ad es. ad una funzione) e l’assegnazione del valore ad una variabile
sono due tipiche situazioni dove viene utilizzata la definizione semplice.
f = Hx^2 − 1L^2
I−1 + x2 M
2
x=2
2
2
Dopo le assegnazioni richiamando l'espressione f Mathematica restituisce la funzione f = I-1 + x2 M calcolata in
x=2:
f
9
Liberando la variabile x:
x =.
l'espressione f torna ad essere una funzione simbolica:
f
I−1 + x2 M
2
Annullando la definizione di f :
Clear@fD
Introduzione all'uso di Mathematica.nb
31
il simbolo f torna ad essere libero:
f
f
à
Esempio 5.1.2
Si verifichino le modalità di esecuzione, richiamo ed annullamento dell’operazione di definizione differita.
Nelle righe che seguono la derivata della funzione f è calcolata attraverso l’operatore D[ ].
f = Hx^2 − 1L^2
I−1 + x2 M
2
D@f, xD
4 x I−1 + x2 M
Si esegua ora la definizione di h come la derivata di f utilizzando l’operazione di definizione semplice. Immeditamamente Mathemathica restituisce l’espressione della derivata di f:
h = D@f, xD
4 x I−1 + x2 M
Si definisca g allo stesso modo ma utilizzando questa volta l’operazione di definizione differita. Mathematica in
questo caso non fornisce output. Per avere l’output (la derivata) è inftti necessario richiamare esplicitamente g . In
altre parole con la definizione differita g non è immediatamente uguale all’espresione derivata ma lo diventa solo se
(e quando) viene richiamata.
g := D@f, xD
g
4 x I−1 + x2 M
Le due identificazioni hanno implicazioni diverse rispetto alle successive operazioni inerenti la funzione f. Ad
esempio richiamando h e g dopo aver modificato f si ottengono risultati diversi:
f = f^2
I−1 + x2 M
4
h
4 x I−1 + x2 M
g
8 x I−1 + x2 M
3
Richiamando h si è ottenuta l’espressione derivata calcolata sulla funzione f senza tener conto della modifica f = f 2
eseguita ossia sull’espressione di f presente nel momento dell’identificazione. Richiamando g si è ottenuta invece
l’espressione derivata della funzione f tenendo conto della modifica f = f 2 eseguita dopo la dichiarazione. La
4
funzione g, se richiamata, è la derivata della funzione f al momento del richiamo (ossia di f = I-1 + x2 M ) e non di f
2
nel momento della dichiarazione (ossia di f = I-1 + x2 M ).
à
Introduzione all'uso di Mathematica.nb
32
Esempio 5.1.3
Si verifichino le modalità di esecuzione dell’operatore di uguaglia in un’equazione.
L’uguaglianza in un’equazione si comporta come un operatore logico:
23
False
33
True
Il simbolo == è utilizzato per formulare e risolvere un'equazione o un sistema di equazioni. Per risolvere un'equazione è buona regola prima assicurarsi che la variabile x sia una variabile libera e poi utilizzare, come visto in
precedenza, con l’operatore Solve[ ]:
x =.
Solve@2 x^2 + 3 x − 2 0, xD
1
:8x → −2<, :x → >>
2
Le soluzioni sono date sotto forma di regole di sostituzione per la variabile x, che rimane non assegnata.
x
x
à
5.2 Funzioni libreria predefinite
Mathematica è in grado di studiare e rappresentare graficamente funzioni reali di variabile reale da a . Le
funzioni più comuni sono già contenute nella librerie del programma (funzioni libreria predefinite) e possono essere
utilizzate semplicemente dopo essere state richiamate in modo corretto. Per richiamare una funzione libreria è
sufficiente scrivere l’identificatore con la prima lettera maiuscola e l’argomento inserito tra parentesi quadrate. La
notazione comunemente usata è F[x]. In particolare, dopo essere state richiamate, le funzioni libreria possono
essere tabulate, graficate, utilizzate per risolvere equazioni o per definire altre funzioni senza richiedere prima
alcuna dichiarazione. Di seguito sono illustrate le funzioni libreria più comuni.
Sqrt[x]
: funzione esponenziale di base e;
: funzione logaritmo in base e;
: funzione logaritmo in base a;
: funzioni trigonometriche;
: funzioni trigonometriche inverse;
: funzioni iperboliche;
: funzione radice quadrata;
Abs[x]
: funzione valore assoluto;
Exp[x]
Log[x]
Log[x,a]
Sin[x], Cos[x], Tan[x]
ArcSin[x], ArcCos[x], ArcTan[x]
Sinh[x], Cosh[x], Tanh[x]
Le funzioni libreria e le funzioni con esse costruite possono essere valutate in un determinato punto a con l’operatore /.x->a . La tabulazione delle stesse funzioni calcolandone i valori numerici punto per punto attraverso l’operatore Table . Gli operatori MatrixForm e ColumnForm consentono di ottenere i dati, rispettivamente, in forma
Introduzione all'uso di Mathematica.nb
Table
MatrixForm
33
ColumnForm
matriciale o come collezione di liste. La rappresentazione grafica delle funzioni è eseguita tramite l’operatore
Plot .
F[x]/.x->a
Table[{x,F[x]},{x,a,b}]
MatrixForm[Table[{x,F[x]},{x,a,b}]]
: valuta la funzione nel punto x=a ;
: calcola la funzione punto per punto nel dominio [a,b]
della variabile indipendente x e fornisce la collezione
di dati numerici in forma di lista di liste;
: fornisce la collezione di dati numerici in forma matri-
ciale;
ColumnForm[Table[{x,F[x]},{x,a,b}]]
Plot[{F[x]},{x,a,b}]
: fornisce la collezione di dati numerici in forma di colonna
di liste;
: produce il grafico nel piano xOy della funzione F[x] nel
dominio [a,b] della variabile indipendente x;
Esempio 5.2.1
Riprendendo l’equazione dell’Esempio 5.1.3 si verifichi la validità del Teorema di Ruffini.
E' sufficiente utilzzare l'operatore di sostituzione /.-> x1 per verificare che le radici dell' equazione verificano la
segenbte espressione Una regola di sostituzione, mediante il comando /. , permette di valutare l' espressione f nel
punto x = 2. Si ottiene :
2 x^2 + 3 x − 2 0
−2 + 3 x + 2 x2 0
Solve@2 x^2 + 3 x − 2 0, xD
1
:8x → −2<, :x → >>
2
La modalità con cui l’operatore Solve restituisce le radici non assegna la variable x alle radici:
x
x
Per assegnare le due soluzioni a due variabili si può usare la regola di sostituzione eseguita mediante l’operatore
/.x->
x ê. 88x → −2<, 8x → 1 ê 2<<
1
:−2, >
2
8a, b< = 8−2, 1 ê 2<
1
:−2, >
2
adesso a e b sono le due soluzioni.
La verifica può essere eseguita come segue:
2 x^2 + 3 x − 2 ê. x → a
0
Introduzione all'uso di Mathematica.nb
34
2 x^2 + 3 x − 2 ê. x → b
0
Naturalmente è di immediata verifica il Teorema di Ruffini, ossia che l’epressione 2 (x-a) (x-b) coincide con il
polinomio che costituisce l’equazione iniziale.
2 Hx − aL Hx − bL
1
2 − + x H2 + xL
2
Expand@%D
−2 + 3 x + 2 x2
à
Esempio 5.2.2
Si consideri la funzione f(x) = cos HxL log H-1 + xL +
Sin@xD
x
. Si tabulino i valori di f in forma (a) di lista di liste, (b)
matricale, (c) di colonna di liste e se ne rappresenti il grafico.
Cos@xD Log@x − 1D + Sin@xD ê x
Sin@xD
Cos@xD Log@−1 + xD +
x
La tabulazione della funzione in termini (a) di lista di liste, (b) matriciali, (c) di colonna di liste e si ottengono
tramite esecuzione degli operatori Table, MatrixForm e ColumnForm:
Table@8x, Cos@xD Log@x − 1D + Sin@xD ê x<, 8x, 0.01, 15<D
880.01, 0.989934 + 3.14144 <, 81.01, −1.61086<,
82.01, 0.446063<, 83.01, −0.648506<,
84.01, − 0.90225<, 85.01, 0.216419<, 86.01, 1.50679<,
87.01, 1.43501<, 88.01, −0.179262<, 89.01, −1.85953<,
810.01, − 1.88769<, 811.01, − 0.0575874<,
812.01, 1.99304<, 813.01, 2.27811<, 814.01, 0.396197<<
MatrixForm@
Table@8x, Cos@xD Log@x − 1D + Sin@xD ê x<, 8x, 0.01, 20<DD;
ColumnForm@
Table@8x, Cos@xD Log@x − 1D + Sin@xD ê x<, 8x, 0.01, 20<DD;
Il simbolo di
; alla fine delle due stringhe precedenti permette di evitare la visualizzazione di tutti i dati nell’out-
put ed in tal modo risparmiare spazio nel Notebook..
Introduzione all'uso di Mathematica.nb
35
Il grafico della funzione è ottenuto attraverso l’operatore Plot e la seguente stringa di input:
Plot@8Cos@xD Log@x − 1D + Sin@xD ê x<, 8x, 0.01, 20<,
PlotRange → 8−4, 4<, PlotStyle → 8Thick, Red<D
4
2
5
10
15
20
−2
−4
à
5.3 Calcolo e rappresentazione di funzioni da in In aggiunta alle funzioni libreria (built-in functions) Mathematica lavora con qualsiasi funzione f[x] a patto che
essa venga correttamente definita dall’utente. Si noti che nel caso di funzioni definite dall’utente è bene utilizzare
un’identificatore (nome simbolico) scritto con prima lettera minuscola (identificatori con prima lettera maiuscola,
come si è visto, indicano le funzioni libreria). Per la dichiarazione di nuove funzioni esistono precise regole di
sintassi. Quando si è definita una nuova funzione la si può utilizzare come quelle di libreria per calcolarne i valori
specifici, per tabularla, per graficarla, per risolvere equazioni, per definire altre funzioni. Per definire una funzione
è necessario stabilirne l’intestazione e il corpo: l’intestazione è data da un identificatore del tipo f[x_], il corpo è
l’espressione matematica che rappresenta effettivamente la funzione. Naturalmente il nome della variabile indipendente è arbitrario (in questo caso si è scelto x). L’associazione tra l’identificatore e il corpo viene eseguita tramite il
simbolo := . Una volta dichiarata la funzione f[x] è possibile calcolarne i valori numerici punto per punto e
ottenerne la rappresentazione in forma di lista di liste attraverso l’operatore Table. Gli operatori MatrixForm e
ColumnForm consentono di ottenere i dati in forma matriciale o come colonna di liste. La rappresentazione grafica
di funzioni è eseguita tramite l’operatore Plot.
f[x_]:= espressione
Table[{x,f[x]},{x,a,b}]
MatrixForm[Table[{x,f[x]},{x,a,b}]]
ColumnForm[Table[{x,f[x]},{x,a,b}]]
Plot[{f[x]},{x,a,b}]
: dichiara una funzione f[x] generica non predefinita;
: calcola la funzione punto per punto nel dominio [a,b]
della variabile x e fornisce la collezione di dati
numerici in forma di lista di liste;
: calcola la funzione punto per punto nel dominio [a,b]
della variabile x e fornisce la collezione di dati
numerici in forma matriciale;
: calcola la funzione punto per punto nel dominio [a,b]
della variabile x e fornisce la collezione di dati
numerici in forma di colonna di liste;
: produce il grafico della funzione f[x] non predefinita nel
dominio [a,b] della variabile indipendente x;
Quando si esegue la dichiarazione di una funzione (f[x_]:= espressione) o si assegna il valore ad una variabile (x=a), Mathematica continua a mantenere valida l’assegnazione fatta per l’intera sessione di lavoro. In taluni
Introduzione all'uso di Mathematica.nb
36
x=a
casi questo può costituire un problema (ad esempio nel caso in cui si debbano dichiarare molte funzioni senza
dover necessariamente cambiare sempre il nome). In questi casi è utile interrompere l’assegnazione fatta in precedenza per poter associare un nome già usato ad una nuova espressione. Una dichiarazione di funzione precedentemente eseguita può essere annullata tramite l'operatore Clear. In modo analogo, è necessario a volte dover interrompere un'assegnazione precedentemente eseguita su una variabile (ad esempio quando a seguito di un'assegnazione eseguita del tipo x=a si voglia evitare che una funzione f(x), definita, porti automaticamente al calcolo di
f(a)). L'annullamento della dichiarazione su una variabile può essere eseguita con l'operatore x=. .
Clear[f]
x=.
: annulla una dichiarazione precedentemente eseguita sulla funzione f[x];
: annulla una dichiarazione precedentemente eseguita sulla variabile x ;
Esempio 5.3.1
Si consideri la funzione f(x) = x2 - x3 . Si tabulino i valori di f in forma (a) di lista di liste, (b) matricale, (c) di
colonna di liste e se ne rappresenti il grafico.
La funzione f[x] non è una funzione predefinita appartenente alle librerie di Mathematica e necessita di essere
dichiarata tramite uguaglianza differita:
f@x_D := x^2 − x^3
f@xD
x2 − x3
Dopo aver dichiarato la funzione è possibile calcolare il valore di f[x] molto facilmente su qualsiasi punto a:
f@aD
a2 − a3
La tabulazione di f[x] in termini di di lista di liste, (b) matricale, (c) di colonna di liste e si ottengono tramite
esecuzione degli operatori Table, MatrixForm e ColumnForm. Per ragioni di spazio nella tabulazione della
funzione f viene omessa la rappresentazione esplicita dei dati. Per fare questo alla fine delle stringhe relative agli
operatori Table, MatrixForm e ColumnForm è stato inserito il simbolo ; . Per evidenziare in modo esplicito i
valori numerici è sufficiente eliminare tale simbolo dalla fine di ogni stringa.
Table@8x, f@xD<, 8x, −10, 10<D;
MatrixForm@Table@8x, f@xD<, 8x, −10, 10<DD;
ColumnForm@Table@8x, f@xD<, 8x, −10, 10<DD;
Introduzione all'uso di Mathematica.nb
37
La rappresentazione grafica della funzione è eseguita con il comando Plot .
Plot@8f@xD<, 8x, − 10, 10<,
PlotRange → 8−800, 800<, PlotStyle −> 8Thick, Red<D
500
−10
−5
5
10
− 500
La dichiarazione eseguita della funzione f[x] (f[x] = x2 − x3 ) se non annullata è mantenuta nella memoria del
Notebook per l'intera sessione di lavoro. Volendo dichiarare una nuova funzione mantenendo il nome f[x] è
necessario, prima della nuova dichiarazione, annullare la dichiarazione precedente:
f@xD
x2 − x3
Clear@fD
f@xD
f@xD
à
Esempio 5.3.2
Si consideri la funzione f(x) =
Sin@xD
x
. Si tabulino i valori di f in forma (a) di lista di liste, (b) matricale, (c) di
colonna di liste e se ne rappresenti il grafico.
La funzione f(x) è una funzione costruita con la funzione sen(x) predefinita appartenente alle librerie di Mathematica. In generale funzioni di questo tipo devono essere dichiarate tramite uguaglianza differita:
f@x_D := Sin@xD ê x
f@xD
Sin@xD
x
La funzione dichiarata è comunque una funzione nota a Mathematica. Nel punto di discontinuità x0 =0 Mathematica associa il corretto valore calcolato dal limite per x tendente a x0 :
f@0D = 1
1
Introduzione all'uso di Mathematica.nb
38
Per rappresentare il grafico della funzione si utilizza l’operatore plo[ ]. L’argomento dell’operatore contiene le
informazioni inerenti lo stile del grafico:
Plot@8f@xD<, 8x, − 10 Pi, 10 Pi<,
PlotStyle −> 8Thick, Red<, PlotRange → 8−0.3, 1.1<D
1.0
0.8
0.6
0.4
0.2
−30
−20
−10
10
20
30
−0.2
à
Una particolare categoria di funzioni importanti per le applicazioni in elettronica e teoria dei segnali solo le funzioni a tratti. In Mathematica le funzioni a tratti si ottengono con l’uso dell’operatore
If abbinato al comando di
uguaglianza imposta = . L’operatore If richiede la definizione di tre argomenti: la condizione, l’azione nel caso di
verifica della condizione, l’azione in caso di falsità della condizione. La struttura è fondamentalmente quella dell’if
...then...else... dei linguaggi di programmazione. Nella definizione di funzioni discontinue il comando di
uguaglianza imposta = viene utilizzato per eliminare le discontinuità eliminabili ossia per imporre un determinato
valore assunto dalla funzione in una sua singolarità x0 (punto di discontinuità). La corretta defnizione di una
funzione a tratti necessita ovviamente della sintassi appropriata.
h[x_]:=If[condizione,f1[x],f2[x]] : dichiara una funzione a tratti del tipo f[x]=f1[x] se la
h[x0]= h0
condizione è verificata, f[x]=f2[x] se la condizione
è negata;
: dichiara il valore imposto h0 della funzione h[x] in
una sua singolarità x0 (punto di discontinuità);
Esempio 5.3.3
senxê x per x < 0
0
per x = 0 e se ne rappresenti il grafico.
Si consideri la funzione a tratti f(x) =
-senxê x per x > 0
h@x_D := If@x  0, Sin@xD ê x, −Sin@xD ê xD
h@0D = 0
0
Per rappresentare il grafico della funzione si utilizza l’operatore plot[ ]. L’argomento dell’operatore contiene le
Introduzione all'uso di Mathematica.nb
39
plot[ ]
informazioni inerenti lo stile del grafico:
Plot@8h@xD<, 8x, − 10 Pi, 10 Pi<,
PlotRange → 8−1.1, 1.1<, PlotStyle −> 8Thick, Red<D
1.0
0.5
− 30
− 20
− 10
10
20
30
−0.5
−1.0
à
5.4 Elementi di calcolo infinitesimale: limiti di funzioni da in Mathematica è in grado di eseguire il calcolo di limiti mediante l’operatore Limit . La freccia si ottiene digitando
- seguito da > . Se il limite destro e il limite sinistro sono diversi Mathematica calcola di defaul il limite destro. Nel
caso Mathematica fornisca un risultato è necessario porre attenzione che il limite potrebbe esistere anche solo da
destra. Per chiedere esplicitamente a Mathematica di calcolare un limite destro o sinistro si usa l’opzione Direction->1 per il limite sinistro o Direction->-1 per il limite destro.
Limit[f, x->x0, Direction->1]
: calcolo di limite per x tendente ad una singolarità x0 da destra.
Limit[f, x->x0, Direction->-1] : calcolo di limite per x tendente ad una singolarità x0 da sinistra.
Limit[f, x->infinity]
Limit[f, x->-infinity]
: calcolo di limite per x tendente a + infinito.
: calcolo di limite per x tendente a - infinito.
Esempio 5.4.1
I seguenti esempi illustrano la corretta sintassi nel calcolo dei limiti.
Limit@Sin@xD ê x, x → 0, Direction −> 1D
1
Limit@Sin@xD ê x, x → 0, Direction −> −1D
1
Limit@x ê Abs@xD, x → 0, Direction −> 1D
−1
Limit@x ê Abs@xD, x → 0, Direction −> −1D
1
Introduzione all'uso di Mathematica.nb
40
Limit@Hx^2 + 2^xL ê H1 + x^ 3L, x −> InfinityD
∞
Limit@Hx^2 + 2^xL ê H1 + x^ 3L, x −> −InfinityD
0
à
Esempio 5.4.2
Nel caso si provi a calcolare un limite che non esiste Mathematica restituisce un output che significa che il limite
1
non esite. Si calcolino ad esempio i limiti delle funzioni (a) f HxL = sen I x M e (b) f HxL = x sen HxL per x che tende a
zero e ad infinito, rispettivamente.
(a)
Sin@1 ê xD
1
SinB F
x
Limit@ Sin@1 ê xD, x → 0D
Interval@8−1, 1<D
L’output significa che il limite non esite e la classe limite è l’intervallo [-1,1].
Plot@8Sin@1 ê xD<, 8x, −3, 3<, PlotStyle −> 8Thick, Red<D
1.0
0.5
−3
−2
−1
1
2
3
−0.5
−1.0
(b)
x Sin@xD
x Sin@xD
Limit@ x Sin@xD, x → InfinityD
Interval@8−∞, ∞<D
L’output significa che il limite non esite e la classe limite è l’intervallo (-Infinito,Infinito).
Introduzione all'uso di Mathematica.nb
41
Plot@8x Sin@xD<, 8x, − 80, 80<, PlotStyle −> 8Thick, Red<D
50
−50
50
−50
à
5.5 Elementi di calcolo infinitesimale: derivate di funzioni da in Mathematica è in grado di eseguire il calcolo di derivate di funzione reali di libreria F[x] o di funzioni f[x] precedentemente dichiarate dall’utente. Per eseguire la derivata è utilizzato l’operatore D con argomenti racchiusi tra parentesi quadre dati dall’espressione della funzione da derivare e dalla variabile rispetto cui derivare. Se la derivata è
di ordine superiore al primo (derivata seconda, terza, ecc.) è necessario specificare, all’interno delle parentesi
quadre, l’espressione della funzione da derivare e la lista costituita dalla variabile e dall’ordine di derivazione. Il
differenziale della funzione si ottiene omettendo di definire la variabile e l’ordine.
D[f[x],x]]
D[f[x],{x,n}]]
D[f[x]]]
: produce la derivata prima della funzione f rispetto a x;
: produce la derivata n-esima della funzione f rispetto a x;
: produce il differenziale della funzione f ;
Esempio 5.5.1
Si consideri la funzione f(x)=
sin HxL
x
sin HxL 2
cos HxL log HxL+
1+log Ix
M
e se ne calcoli la derivata f '(x) . Si rappresentino graficamente
la funzione f (x) e f '(x).
Conviene prima dichiarare la funzione:
f@x_D := HCos@xD Log@xD + Sin@xD ê xL ê H1 + Log@x^ HSin@xDLD^2L
verificare la dichiarazione eseguita:
f@xD
Cos@xD Log@xD +
Sin@xD
x
1 + LogAxSin@xD E
2
Introduzione all'uso di Mathematica.nb
42
e poi eseguirne la derivata:
D@f@xD, xD
−
2 LogAxSin@xD E ICos@xD Log@xD +
Sin@xD 2
M
x
J1 + LogAxSin@xD E N
+
2 2
2 Cos@xD
x
−
Sin@xD
x2
− Log@xD Sin@xD
1 + LogAxSin@xD E
2
I grafici di f (x) e f '(x) permettono di verificare la correttezza del calcolo eseguito. Ancora una volta conviene
prima dichiarare la funzione derivata:
derf@x_D := −
2 LogAxSin@xD E ICos@xD Log@xD +
2
J1 + LogAxSin@xD E N
2 Cos@xD
x
−
Sin@xD
x2
Sin@xD 2
M
x
+
2
− Log@xD Sin@xD
1 + LogAxSin@xD E
2
verificare la dichiarazione eseguita:
derf@xD
−
2 LogAxSin@xD E ICos@xD Log@xD +
Sin@xD 2
M
x
J1 + LogAxSin@xD E N
+
2 2
2 Cos@xD
x
−
Sin@xD
x2
− Log@xD Sin@xD
1 + LogAxSin@xD E
2
e solo successivamente rappresentare, come richiesto, il grafico delle funzioni f[x] e derf[x] dechiarate:
Plot@8f@xD, derf@xD<, 8x, −0.1 Pi, 10 Pi<, PlotRange → 8−8., 8.<,
PlotStyle −> 8Thick, Red<, PlotStyle −> 8Thick, Blue<D
5
5
10
15
20
25
30
−5
à
Introduzione all'uso di Mathematica.nb
43
5.6 Elementi di calcolo infinitesimale: primitive di funzioni da in Mathematica calcola l’integrale indefinito di una funzione f[x] mediante l’uso dell’operatore Integrate con
argomenti dati dalla funzione integranda e dalla variabile rispetto alla quale integrare. Gli integrali indefiniti
prodotti da Mathematica non riportano la costante addittiva indeterminata. Nel caso la primitiva non fosse una
funzione elementare Mathematica non produce risultato.
: produce il calcolo della primitiva della funzione f[x] a meno di una costante
addittiva arbitraria.
Integrate[f[x],x]
Esempio 5.6.1
1+x
Si calcoli la primitiva della seguente funzione integrabile in : f(x)= 1+x+x
;
2
f@xD = H1 + xL ê H1 + x + x^ 2L
1+x
1 + x + x2
Integrate@f@xD, xD
ArcTanB
1+2 x
3
F
1
+
2
3
LogA1 + x + x2 E
Per verificare che il risultato è corretto eseguiamo la derivata della primitiva trovata a meno di una costante arbitraria k:
ArcTanB
1+2 x
3
Fx =
1+2 x
3
k+
F
2
I1 + x + x2 M
+
1
2
3
D@Fx, xD
1+2 x
+
1
2
3
ArcTanB
F
+
LogA1 + x + x2 E + k
LogA1 + x + x2 E
2
3 I1 +
1
3
H1 + 2 xL2 M
FullSimplify@%D
1+x
1 + x + x2
à
Esempio 5.6.2
Si calcoli la primitiva della funzione f HxL =
f@xD = 1 ê HArcTan@xDL
1
ArcTan@xD
1
arctan HxL
:
Introduzione all'uso di Mathematica.nb
44
Integrate@f@xD, xD
1
x
‡
ArcTan@xD
La primitiva non è una funzione elementare e Mathematica restituisce la funzione integranda inalterata.
à
Esempio 5.6.3
Si calcoli la primitiva della funzione f HxL =
1
log HxL
:
In questo caso Mathematica è in grado di fornire il risultato anche se la primitiva non una funzione elementare.
f@xD = 1 ê Log@xD
1
Log@xD
Integrate@1 ê Log@xD, xD
LogIntegral@xD
Per Mathematica LogIntegral[x] è la funzione f(x)=log(Ÿ x x) ed in effetti questa è la primitiva, definita a meno
della costante arbitraria, della dunzione f iniziale.
Il risultato trovato è di immediata verifica:
D@ LogIntegral@xD, xD
1
Log@xD
à
5.7 Calcolo di integrali definiti esatto ed approssimato
La sintassi per il calcolo dell'integrale definito di una funzione f[x] nell'intervalloa [a,b] prevede l'utilizzo dell'operatore Integrate con argomento costituito dal corpo della funzione da integrare e da una stringa contenente la
variabile di integrazione e gli estremi. Il comando Integrate calcola, se possibile, un integrale definito in modo
esatto, passando attraverso la primitiva o con altri metodi esatti. Quando questo non fosse possibile, ossia nel caso
di integrali definiti caratterizzati da calcoli di primitive non elementari, Mathematica non produce risultato. In tal
caso è possibile eseguire il calcolo approssimato dell’integrale definito coi metodi dell’analisi numerica. Il calcolo
del valore approssimato utilizza l’operatore NIntegrate con lo stesso argomento utilizzato nel caso del calcolo
dell’integrale esatto.
: produce il calcolo dell'integrale definito di una funzione f[x] nell'intervallo
di integrazione [a,b] ;
NIntegrate[f[x],{x,a,b}] : produce il calcolo approssimato dell’integrale definito di una funzione f[x]
nell’intervallo di integrazione [a,b] ;
Integrate[f[x],{x,a,b}]
Esempio 5.7.1
Si calcoli il valore dell'integrale definito della funzione f HxL =
1+x
1+x+x2
nell’intervallo di integrazione [0,1].
Introduzione all'uso di Mathematica.nb
45
f@xD = H1 + xL ê H1 + x + x^ 2L
1+x
1 + x + x2
Integrate@f@xD, 8x, 0, 1<D
1
J 3 π + 9 Log@3DN
18
Per capire l'entità del numero calcolato è utile avere il risultato in termini di numeri decimali.
1
J 3 π + 9 Log@3DNF
18
0.851606
NB
à
Esempio 5.7.2
Si calcoli il valore dell’integrale definito della funzione f HxL =
1
1+‰x +x
nell’intervallo di integrazione [0,1].
Nel caso della funzione considerata calcolo della primitiva con metodi esatti non produce risultato:
f@xD = 1 ê H1 + Exp@xD + xL
1
1 + x + x
Integrate@f@xD, 8x, 0, 1<D
1
1
x
‡
x
0 1+ +x
Al contrario il calcolo dell’integrale approssimato produce output numerico:
NIntegrate@f@xD, 8x, 0, 1<D
0.329971
à
Esempio 5.7.3
Si consideri la funzione f HxL =
1
1+x2
si calcoli l’integrale definito nell’intervallo [0,1] in forma esatta (utilizzando
Integrate)e in forma approssimata (con NIntegrate ). Si confrontino i risultati ottenuti.
f@xD = 1 ê H1 + x ^2L
1
1 + x2
Integrate@f@xD, 8x, 0, 1<D
π
4
NIntegrate@f@xD, 8x, 0, 1<D
0.785398
Introduzione all'uso di Mathematica.nb
46
Si osservi che:
N@Pi ê 4D
0.785398
cioè il valore “approssimato” è approssimato davvero bene.
à
5.8 Integrali generalizzati (cenni)
Mathematica è in grado di calcolare integrali definiti generalizzati in forma esatta purchè, ovviamente, risultino
convergenti. In caso di non convergenza è possibile tentare il calcolo approssimato degli integrali mediante opportuni algoritmi.
Esempio 5.8.1
1
1
Si calcoli l’integrale definito generalizzato Ÿ0
x
dx .
f@xD = 1 ê Sqrt@xD
1
x
Integrate@f@xD, 8x, 0, 1<D
2
L’integrale converge ed è calcolabile esattamente.
à
Esempio 5.8.2
+¶
2
Si calcoli l’integrale definito generalizzato Ÿ-¶ ‰-x dx .
f@xD = Exp@−x^ 2D
2
−x
Integrate@f@xD, 8x, − Infinity, Infinity<D
π
L’integrale converge ed è calcolabile esattamente.
à
Esempio 5.8.3
11
Si calcoli l’integrale definito generalizzato Ÿ0
f@xD = 1 ê x
1
x
x
dx .
Introduzione all'uso di Mathematica.nb
47
Integrate@f@xD, 8x, 0, 1<D
— Integrate::idiv : Integral of
‡
1
0
1
1
x
does not converge on 80, 1<. à
x
x
L’integrale non converge. In questo caso Mathematica non produce risultato e fornisce un messaggio di testo in cui
è dichiarata la non convergenza.
Tentando di risolvendo l’integrale in forma approssimata Mathematica fornisce un risultato numerico ma mette in
guardia sul fatto che la convergenza dell’algoritmo di approssimazione è lenta.
NIntegrate@f@xD, 8x, 0, 1<D
— NIntegrate::slwcon :
Numerical integration converging too slowly; suspect one of the
following: singularity , value of the integration is 0, highly
oscillatory integrand, or WorkingPrecision too small. à
— NIntegrate::ncvb :
NIntegrate failed to converge to prescribed accuracy after 9
recursive bisections in x near 8x< = 91.22413 µ 10-225 =.
NIntegrate obtained 191612.2902185145` and
160378.51781028978` for the integral and error estimates. à
191 612.
In questa situazione l’output prodotto è certamente inattendibile.
à
5.9 Equazioni differenziali (cenni)
Mathematica è in grado di risolvere in modo esatto equazioni differenziale semplici. La sintassi per esprimere le
equazioni differenziali prevede per la funzione incognita la forma y[x]. La variabile all’interno delle parentesi
quadre è ovviamenete arbitraria. Le derivate sono espresse nella forma y'[x], y''[x], y'''[x] ... , e tra i due membri
dell’equazione è inserito il imbolo
==. Mathematica utilizza l’operatore
DSolve per risolvere le equazioni
differenziali.
: produce il calcolo di equazioni differenziali
lineari del primo ordine.
DSolve[A[x]y''[x]+B[x]y’[x]+C[x]y==D[x],y[x],x] : produce il calcolo di equazioni differenziali
lineari del secondo ordine.
DSolve[A[x]y’[x]+B[x]y[x]==D[x],y[x],x]
Esempio 5.9.1
Si calcoli l’equazione differenziale lineare del primo ordine: y'(x) + x y(x) = x .
DSolve@y'@xD + x y@xD x, y@xD, xD
::y@xD → 1 + − 2 C@1D>>
x2
Introduzione all'uso di Mathematica.nb
48
Mathematica produce le soluzioni indicando con C[1] la costante arbitraria di integrazione.
à
Esempio 5.9.2
Si calcoli l’equazione differenziale lineare, del secondo ordine, a coefficienti costanti, non omogenea: y''(x) + 3y'(x)
- 2 y(x) = sen(x) .
DSolve@y''@xD + 3 y '@xD − 2 y@xD Sin@xD, y@xD, xD
3
17
3
17
4 HCos@xD + Sin@xDL
− −
x
− +
x
::y@xD → 2 2
C@1D + 2 2
C@2D +
>>
3 J− 5 + 17 N J5 + 17 N
à
Esempio 5.9.3
Si calcoli l’equazione differenziale, del primo ordine, a variabili separabili: coefficienti costanti, anche non omogenea: y(x) y'(x) = x2 .
DSolve@y@xD y'@xD x^ 2, y@xD, xD
::y@xD → −
2
3
x3 + 3 C@1D >, :y@xD →
2
3
x3 + 3 C@1D >>
à
6 Rappresentazione di curve nel piano e nello spazio e di superfici nello spazio
6.1 Equazioni parametriche di curve in 2 e 3
2 e 3 possono essere opportunamente descritte e rappresentate attraverso equazioni parametriche. In
generale equazioni parametriche di curve in 2 e in 3 sono esprimibili, rispettivamente, come mappe da a 2
(f: Ø2 ) e da a 3 (f: Ø3 ). A seconda dei casi (e comunque nei casi più semplici) le equazioni parametCurve in
riche possono essere espresse in termini di coordinate cartesiane, polari o cilindriche. In Mathematica le equazioni
parametriche vanno scritte utilizzando il simbolo = . La rappresentazione grafica dei supporti delle curve in 2 e in
3 è eseguita in attraverso i comandi parametricPlot e parametricPlot3D , rispettivamente.
: definisce la parametrizzazione di una curva in 2 ;
f:={{x[t],y[t],z[t]},{t,a,b}}
: definisce la parametrizzazione di una curva in 3 ;
parametricPlot[{x[t],y[t]},{t,a,b}]
: produce il sostegno (grafico) di una curva in 2
descritta tramite equazioni parametriche
del tipo f[t]={x[t], y[t]} al variare di t in [a,b];
parametricPlot3D[{x[t],y[t],z[t]},{t,a,b}] : produce il sostegno di una curva in 3 descritta
tramite equazioni parametriche del tipo
f[t]={x[t], y[t], z[t]} al variare di t in [a,b];
f:={{x[t],y[t]},{t,a,b}}
Introduzione all'uso di Mathematica.nb
49
Esempio 6.1.1
Si rappresenti sul piano 2 l'arco spirale di Archimede caratterizzato da due giri e mezzo .
Le equazioni parametriche per la spirale di archimede sul piano possono essere scritte nella seguente forma:
x(t)= t cos(t)
y(t)= t sen(t)
con 0 § t § n 2p dove n rappresenta il numero dei giri della spirale. In particolare nell’esempio considerato vale 0
§ t § (5/2) 2p.
Tradotte in sintassi di Mathematica le equazioni parametriche della spirale si scrivono:
x@t_D = t Cos@tD
t Cos@tD
y@t_D = t Sin@tD
t Sin@tD
e in termini di liste:
spir@t_D = 8t Cos@tD, t Sin@tD<
8t Cos@tD, t Sin@tD<
con 0 § t § 5 p .
La rappresentazione grafica della spirale è data dal sostegno della curva in 2 :
ParametricPlot@8x@tD, y@tD<,
8t, 0, 5 Pi<, PlotStyle −> 8Thick, Red<D
10
5
− 15
− 10
−5
5
10
−5
− 10
A partire dalle equazioni parametriche di una curva è possibile calcolare la sua lunghezza. Per far questo è prima
necessario definire una funzione lunghezza. Tale funzione è esprimibile tramite la seguente stringa di comandi (la si
prenda come definizione):
lungh[curv_,a_,b_]:=Integrate[Simplify[Sqrt[D[curv,t].D[curv,t]]],{t,a,b}]
dove l’espressione curv indica la parametrizzazione della curva eseguita rispetto al parametro t variabile tra gli
estremi a e b .
Introduzione all'uso di Mathematica.nb
50
La lunghezza della spirale è quindi calcolata definendo la funzione lunghezza:
lungh@curv_, a_, b_D :=
Integrate@Simplify@Sqrt@D@curv, tD.D@curv, tDDD, 8t, a, b<D
e applicando tale funzione alle equazioni parametriche della spirale (spir[t]) con estremi a e
b , nel caso
presente, rispettivamente, 0 e 5p :
lungh@spir@tD, 0, 5 PiD
1
5 π 1 + 25 π2 + ArcSinh@5 πD
2
1
5π
2
125.344
NB
1 + 25 π2 + ArcSinh@5 πD F
à
Esempio 6.1.2
L’estensione al caso della spirale rappresentata in 3 è immediata.
Parametrizzazione dell’arco spirale di Archimede in 3 :
x(t) = t cos(t)
y(t) = t sen(t)
z(t) = t
con 0 § t § 5p .
Tradotte in sintassi di Mathematica, le equazioni parametriche della spirale in
seguente:
x@t_D = t Cos@tD
t Cos@tD
y@t_D = t Sin@tD
t Sin@tD
z@t_D = t
t
e tramite liste :
spir@t_D = 8t Cos@tD, t Sin@tD, t<
8t Cos@tD, t Sin@tD, t<
sempre con 0 § t § 5 p .
3 si possono scrivere nella forma
Introduzione all'uso di Mathematica.nb
51
La rappresentazione è data dal sostegno della curva in 3 :
ParametricPlot3D@8x@tD, y@tD, z@tD<,
8t, 0, 5 Pi<, PlotStyle −> 8Thick, Red<D
15
10
5
10
0
-10
0
0
-10
10
La lunghezza della spirale in 3 è calcolata definendo la funzione lunghezza (la stringa continua a valere anche con
curve in 3 ) :
lungh@curv_, a_, b_D :=
Integrate@Simplify@Sqrt@D@curv, tD.D@curv, tDDD, 8t, a, b<D
e applicando tale funzione alle equazioni parametriche della spirale (spir[t]) con estremi a e b , rispettivamente, 0 e 5p :
lungh@spir@tD, 0, 5 PiD
5
5π
F
π 2 + 25 π2 + ArcSinhB
2
2
NB
5
π
2
126.972
2 + 25 π2 + ArcSinhB
5π
2
FF
Appare curioso che la differenza di lunghezza tra la spirale in
intuitivamente ci sarebbe aspettata.
2 e quella in 3 appare minore di quella che
à
6.2 Equazioni parametriche di superfici in 3
Superfici in 3 possono essere opportunamente descritte e rappresentate attraverso equazioni parametriche. In
generale equazioni parametriche di superfici in 3 sono esprimibili come mappe da 2 a 3 (f: 2 Ø3 ). A
seconda dei casi (e comunque nei casi più semplici) le equazioni parametriche possono essere espresse in termini di
coordinate cartesiane, polari o cilindriche. In Mathematica le equazioni parametriche vanno scritte utilizzando il
simbolo = . La rappresentazione grafica dei supporti delle curve in 3 è eseguita tramite l’operatore parametric-
Introduzione all'uso di Mathematica.nb
52
=
parametric-
Plot3D.
f:={{x[u,v],y[u,v],z[u,v]},{u,a,b},{v,c,d}}
definisce la parametrizzazione di una superficie in
:
;
3
parametricPlot3D[x[u,v],y[u,v],z[u,v],{u,a,b},{v,c,d}] :
produce il sostegno di una superficie in 3 descritta tramite equazioni parametriche del tipo
f[u, v]={x[u, v],y[u, v],z[u, v]]} al variare di u in [a,b] e di v in [c,d];
Esempio 6.2.1
Si rappresenti un toro di raggio equatoriale R e raggio meridiano r immerso nello spazio 3 .
La parametrizzazione di un toro di raggio equatoriale R e meridiano r può essere scritta nella forma:
x(u,v) = (R+rcos(u)) cos(v)
y(u,v) = (R+rcos(u)) sen(v)
z(u,v) = sen(u)
con 0 § u § 2p , 0 § v § 2p .
tradotta in sintassi di mathematica (con R=6, r=2):
x@u_, v_D = H6 + 2 Cos@uDL Cos@vD
H6 + 2 Cos@uDL Cos@vD
y@u_, v_D = H6 + 2 Cos@uDL Sin@vD
H6 + 2 Cos@uDL Sin@vD
z@u_, v_D = Sin@uD
Sin@uD
e in termini di liste:
toro@t_D = 8x@u, vD, y@u, vD, z@u, vD<
8H6 + 2 Cos@uDL Cos@vD, H6 + 2 Cos@uDL Sin@vD, Sin@uD<
con 0 § u § 2p , 0 § v § 2p .
La rappresentazione è data dal sostegno della superficie in 3 :
ParametricPlot3D@8x@u, vD, y@u, vD, z@u, vD<,
8u, 0, 2 Pi<, 8v, 0, 2 Pi<D
Introduzione all'uso di Mathematica.nb
53
La rappresentazione del toro eseguita prende in considerazione R e r fissi. Se si vuole considerare R e r come
variabili si deve ridefinire la parametrizzazione della superficie in termini di R e r variabile:
x@R_, r_D = HR + r Cos@uDL Cos@vD
HR + r Cos@uDL Cos@vD
y@R_, r_D = HR + r Cos@uDL Sin@vD
HR + r Cos@uDL Sin@vD
z@R_, r_D = Sin@uD
Sin@uD
A questo punto la rappresentazione di tori caratterizzati da diversi valori di R e r è immediata:
Tori@R_, r_D := ParametricPlot3D@
8x@R, rD, y@R, rD, z@R, rD<, 8u, 0, 2 Pi<, 8v, 0, 2 Pi<D
Tori@6, 5D
à
Esempio 6.2.2
Si realizzi un’animazione della superfie del toro mantenendo di raggio equatoriale R fisso e facendo variare in
modo dinamico il raggio meridiano dal valore iniziale r=1 al valore finale r=6.
Mathematica realizza un’animazione su una determinata superficie utilizzando le equazioni parametriche che
descrivono la superfice stessa e iterando in modo dinamico uno dei parametri che la caratterizzano. Per introdurre
animazioni dinamiche su curve e superfici descritte mediante equazioni parametriche si usa l’operatore Manipulate.
Per realizzare l’animazione richiesta si deve considerare la parametrizzazione (realizzata nell’esempio precedente)
dei tori di raggio equatoriale R e di raggio meridiano r:
x@R_, r_D = HR + r Cos@uDL Cos@vD
HR + r Cos@uDL Cos@vD
y@R_, r_D = HR + r Cos@uDL Sin@vD
HR + r Cos@uDL Sin@vD
Introduzione all'uso di Mathematica.nb
54
z@R_, r_D = Sin@uD
Sin@uD
Tori@R_, r_D := ParametricPlot3D@
8x@R, rD, y@R, rD, z@R, rD<, 8u, 0, 2 Pi<, 8v, 0, 2 Pi<D
(con 0 § u § 2p , 0 § v § 2p )
e utilizzare il comando Manipulate per tenere fisso il raggio equatoriale (R=6) e far scorrere il parametro r (da
r=1 a r=6). Il parametro di finezza dell’animazione è stato posto in modo arbirario uguale a 0.1
Manipulate@Tori@6, rD, 8r, 1, 6, 0.1<D
r
3.
à
6.3 Rappresentazione di curve e superfici in forma implicita
Curve e superfici possono essere descritte anche attraverso equazioni espresse in forma implicita in assenza di
parametrizzazione. Equazioni del tipo f(x, y) = 0 e f(x ,y, z) = 0 possono rappresentare rispettivamente equazioni di
curve in 2 e superfici in 3 . Mathematica è in grado di rappresentare curve e superfici in forma implicita a
condizione di importare un apposito Package (Graphics’ContourPlot3D’) e utilizzando il comando ContourPlot
e ContourPlot3D. Si noti che nelle versioni di Mathematica più recenti il Package è incluso di defaul
all’interno del Kernel e in tal modo non vi è la necessita di eseguire il comando di richiamo.
: carica il package di Mathematica per
rappresentare superfici espresse in forma
implicita (i.e. da equazioni del tipo
f(x, y, z) = 0) ;
ContourPlot3D[f(x,y,z),{x,a,b},{y,c,d},{z,e,f}] : produce il grafico di una superficie in 3
espressa in forma implicita ;
<<Graphics’ContourPlot3D’
Introduzione all'uso di Mathematica.nb
55
Esempio 6.3.1
Si rappresenti la superficie della sfera descritta in forma implicita dall’equazione x2 + y2 + z2 = 4 e la si intersechi
con il piano z = x - y.
L’equazione che rappresenta in forma implicita la superfice sferica si scrive: x2 + y2 + z2 - 4 = 0. Il grafico dell’equazione in questione si ottiene con la seguente stringa di comando:
ContourPlot3D@x^2 + y^2 + z^2 − 9 0,
8x, − 3, 3<, 8y, −3, 3<, 8z, −3, 3<D;
L’equazione che rappresenta in forma implicita il piano si scrive: z - x + y = 0. Il grafico dell’equazione in questione si ottiene con la seguente stringa di comando:
ContourPlot3D@−x + y + z == 0, 8x, − 3, 3<, 8y, −3, 3<, 8z, −3, 3<D;
L’intersezione tra due superfici generiche si ottiene in modo semplice con il comando Show[s1, s2] dove con s1 e
s2 si sono indicate le stringhe di rappresentazione ContourPlot3D delle due superfici.
s1 = ContourPlot3D@x^2 + y^2 + z^2 − 9 0,
8x, −3, 3<, 8y, −3, 3<, 8z, − 3, 3<D;
s2 = ContourPlot3D@−x + y + z == 0,
8x, −3, 3<, 8y, −3, 3<, 8z, − 3, 3<D;
Show@s1, s2D
à
6.4 Rappresentazione di funzioni a più variabili
E’ noto che una funzione a due variabili f(x, y) è rappresentata da una superficie in 3 . In Mathematica la rappresentazione di una funzione f[x,y] in 3 è eseguita utilizzando l’operatore Plot3D. La sintassi richiesta nei comandi
di input segue sostanzialmente quella già vista, con l’operatore Plot, per la rappresentazione dei grafic delle
funzioni f[x] ad una variabile. Gli argomenti inseriti nelle parentesi quadre dell’operatore Plot3d devono ovviamente tenere conto del dominio di entrambe le variabili x e y.
Plot[{f[x]},{x,a,b}]
Plot3D[{f[x,y]},{x,a,b},{y,c,d}]
: produce il grafico della funzione f[x] nei domini [a,b] della
variabile indipendenti x;
: produce il grafico della funzione f[x,y] nei domini [a,b] e [c,d]
della variabili indipendenti x e y , rispettivamente;
Introduzione all'uso di Mathematica.nb
56
Esempio 6.4.1
Si rappresenti la funzione f(x,y) = x 2 - 2y2 - 5xy nel dominio C={(x,y) t.c. °x2 + y2 § 0.1 †} . La funzione f mappa punti
da C Õ 2 su 3 ed è rappresentabile da una superfice nello spazio 3 .
Dopo aver definito opportunamente la funzione la rappresentazione di f(x,y) è immediata nell’insieme Q del piano
xy corrispondente al quadrato di lato 6 e centrato sull’origine (insieme Q={(x,y) t.c. † x † § 3 † , †y † § 3 † }.
f@x_, y_D := 8 x^ 2 − 3 y^ 2 − 10 x y
f@x, yD
8 x2 − 10 x y − 3 y2
Plot3D@f@x, yD, 8x, −1, 1<, 8y, −3, 3<D
La rappresentazione di f(x,y) nel dominio C è più complicata. Per avere il grafico di f nel cerchio di raggio R=0.1
(insieme di punti C) è necessario parametrizzare f sui punti del cerchio espressi per semplicità in coordinate polari.
La rappresentazione della superficie di f espressa in forma parametrica è eseguita tramite il comando ParametricPlot.
x@r_, θ_D = r Cos@θD
r Cos@θD
y@r_, θ_D = r Sin@θD
r Sin@θD
In termini di liste la parametrizzazione può essere riscritta come segue:
sup@r_, θ_D = 8r Cos@θD, r Sin@θD<
8r Cos@θD, r Sin@θD<
con 0≤r≤0.01 e 0≤θ<5π.
Introduzione all'uso di Mathematica.nb
57
Alla fine la rappresentazione della funzione f(x,y) nel dominio C diventa:
ParametricPlot3D@8x@r, θD, y@r, θD, f@x@r, θD, y@r, θDD<,
8r, 0, 0.1<, 8θ, 0, 2 Pi<, PlotPoints −> 820, 30<D
à