27-09-2012
10:05
Pagina 1
1
A2 • Bipoli elettrici e loro collegamenti
Esercizi aggiuntivi – Unità A2
Esercizi svolti
Esercizio 1
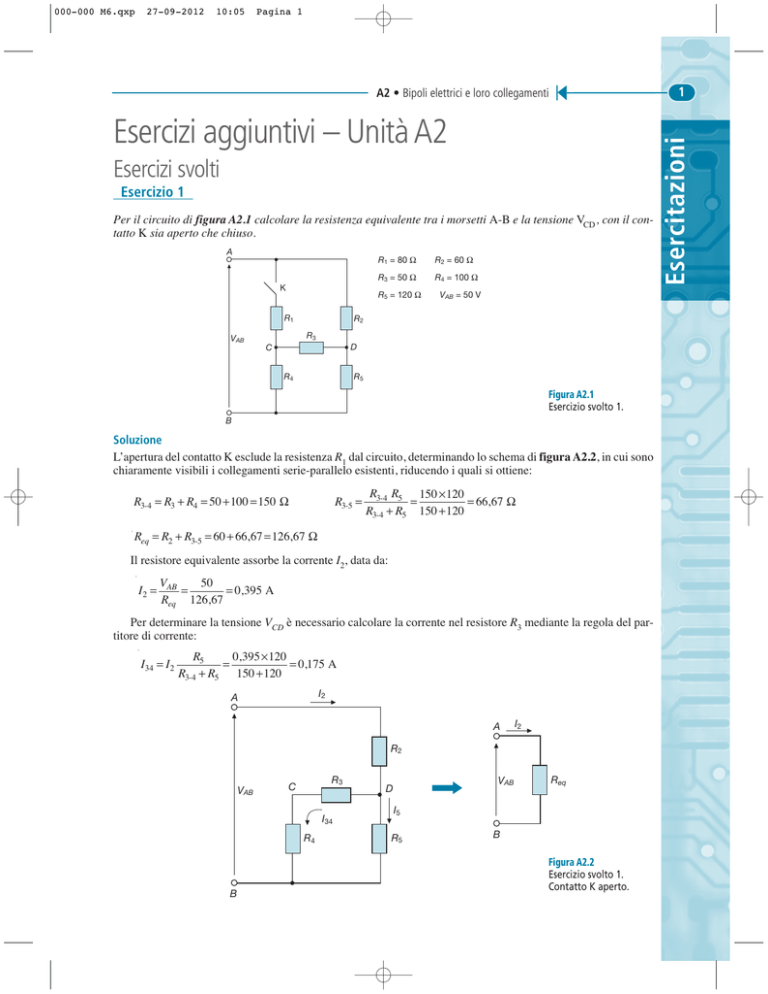
Per il circuito di figura A2.1 calcolare la resistenza equivalente tra i morsetti A-B e la tensione VCD , con il contatto K sia aperto che chiuso.
A
K
R1 = 80 Ω
R2 = 60 Ω
R3 = 50 Ω
R4 = 100 Ω
R5 = 120 Ω
R1
VAB = 50 V
R2
R3
VAB
D
C
R4
R5
Figura A2.1
Esercizio svolto 1.
B
Soluzione
L’apertura del contatto K esclude la resistenza R1 dal circuito, determinando lo schema di figura A2.2, in cui sono
chiaramente visibili i collegamenti serie-parallelo esistenti, riducendo i quali si ottiene:
R3-4 = R3 + R4 = 50 + 100 = 150 Ω
R3-5 =
R3-4 R5 150 × 120
=
= 66, 67 Ω
R3-4 + R5 150 + 120
Req = R2 + R3-5 = 60 + 66, 67 = 126, 67 Ω
Il resistore equivalente assorbe la corrente I2, data da:
I2 =
VAB
50
=
= 0, 395 A
Req 126, 67
Per determinare la tensione VCD è necessario calcolare la corrente nel resistore R3 mediante la regola del partitore di corrente:
I34 = I2
R5
0, 395 × 120
=
= 0,175 A
R3-4 + R5 150 + 120
I2
A
A
I2
R2
VAB
R3
C
I34
R4
B
VAB
D
Req
I5
R5
B
Figura A2.2
Esercizio svolto 1.
Contatto K aperto.
Esercitazioni
000-000 M6.qxp
000-000 M6.qxp
27-09-2012
10:05
Esercitazioni
2
Pagina 2
Modulo A • Grandezze elettriche fondamentali e loro legami, bipoli elettrici
Tenendo presente che la corrente I3-4 circola dal punto D (punto a potenziale maggiore) al punto C (potenziale
minore), la tensione VCD sarà negativa:
VCD = − R3 I34 = − 50 × 0,175 = − 8, 75 V
Con il contatto K chiuso il circuito assume la struttura a ponte riportata nella figura A2.3 e occorre quindi ricorrere a una trasformazione stella-triangolo o viceversa. Trasformando il triangolo R1-R2-R3 nella stella equivalente RA, RC, RD, si ottiene lo schema di figura A2.4, riducendo il quale si calcola la resistenza equivalente:
RA =
R1 R2
80 × 60
=
= 25, 26 Ω
R1 + R2 + R3 80 + 60 + 50
RC =
R1 R3
80 × 50
=
= 21, 05 Ω
R1 + R2 + R3 80 + 60 + 50
RD =
R2 R3
60 × 50
=
= 15, 79 Ω
R1 + R2 + R3 80 + 60 + 50
R4 C = R4 + RC = 100 + 21, 05 = 121 Ω
Req = RA +
R5 D = R5 + RD = 120 + 15, 79 = 135,8 Ω
R4 C R5 D
121 × 135, 8
= 25, 26 +
= 89, 25 Ω
R4 C + R5 D
121 + 135, 8
La corrente circolante nel resistore equivalente è data da:
I=
VAB
50
=
= 0, 56 A
Req 89, 25
Le correnti circolanti nei due rami in parallelo sono pari a:
I4C = I
R5 D
0, 56 × 135,8
=
= 0, 296 A
R4 C + R5 D 121 + 135,8
I5 D = I − I4 C = 0, 56 − 0, 296 = 0, 264 A
Per calcolare la tensione VCD si applica la formula della tensione tra due punti; scegliendo il percorso RC -RD
e tenendo conto dei segni delle tensioni sui due resistori si ottiene:
VCD = − RC I4 C + RD I5 D = −21, 05 × 0, 296 + 15, 79 × 0, 264 = −2, 06 V
Allo stesso risultato si arriva scegliendo il percorso R4-R5:
VCD = R4 I4 C − R5 I5 D = 100 × 0, 296 − 120 × 0, 264 = −2, 06 V
A
A
I
RA
R1
RC
VAB
RA
R2
RD
A
D
C
I4C
I5D
RC
RD
R3
VAB
R4
VAB
Req
R5
D
C
R4
B
Figura A2.3
Esercizio svolto 1.
Contatto K chiuso.
I
B
B
R5
Figura A2.4
Esercizio svolto 1.
Trasformazione dello
schema di figura A2.3.
000-000 M6.qxp
27-09-2012
10:05
Pagina 3
A2 • Bipoli elettrici e loro collegamenti
3
Per il circuito di figura A2.5 calcolare le correnti nei vari rami, la tensione VAC , le potenze assorbite dalle singole resistenze, la f.e.m. del generatore, le potenze (generata, utile e persa) e il rendimento del generatore.
I
R3
A
Ri = 5 Ω
I34
R1 = 100 Ω R2 = 50 Ω
I12
+
R1
E
VAB = 50 V
R4
R3 = 60 Ω
R4 = 40 Ω
R5 = 80 Ω
R6 = 20 Ω
B
Ri
R2
R5
R6
I5
I6
Figura A2.5
Esercizio svolto 2.
C
Soluzione
In questo tipo di problema è nota una delle grandezze del circuito alimentato dal generatore, in questo caso la tensione VAB ai capi della serie R3-R4, e pertanto il dato di partenza è proprio tale tensione. Risolvendo il lato A-B si
ricava la corrente I34, da cui è poi facile risalire alle correnti I5 e I6:
I34 =
VAB
50
=
= 0, 5 A
R3 + R4 60 + 40
I5 = I34
R6
0, 5 × 20
=
= 0,1 A
R5 + R6 80 + 20
I6 = I34 − I5 = 0, 5 − 0,1 = 0, 4 A
La tensione tra i nodi A e C si calcola con la formula della tensione tra due punti, scegliendo un percorso lungo
la parte di circuito già risolta:
VAC = VAB + R5 I5 = 50 + 80 × 0,1 = 58 V
Si determinano quindi le correnti rimanenti:
VAC
58
I = I12 + I34 = 0, 387 + 0, 5 = 0,887 A
=
= 0, 387 A
R1 + R2 100 + 50
La f.e.m. è calcolabile dalla formula della caratteristica esterna del generatore:
I12 =
E = VAC + Ri I = 58 + 5 × 0,887 = 62, 43 V
Il calcolo delle potenze assorbite dai singoli resistori alimentati dal generatore è immediato:
2
P1 = R1 I12
= 100 × 0, 3872 = 15 W
2
P2 = R2 I12
= 50 × 0, 3872 = 7, 5 W
2
P3 = R3 I34
= 60 × 0, 52 = 15 W
2
P4 = R4 I34
= 40 × 0, 52 = 10 W
P5 = R5 I52 = 80 × 0,12 = 0,8 W
P6 = R6 I62 = 20 × 0, 4 2 = 3, 2 W
Con le formule tipiche del generatore reale di tensione si determinano le potenze e il rendimento, tenendo
conto che la tensione ai capi del generatore corrisponde alla VAC :
Pg = EI = 62, 43 × 0, 887 = 55, 37 W
Pu = VAC I = 58 × 0,887 = 51, 4 W
Pp = Pg − Pu = 55, 37 − 51, 4 = 3, 97 W
η=
Pu 51, 4
=
= 0, 928
Pg 55, 37
È possibile verificare il bilancio energetico del circuito: la somma delle potenze assorbite dai resistori di carico deve essere pari alla potenza utile del generatore, che è la potenza che il generatore eroga al carico collegato
ai suoi morsetti. Con i valori calcolati si ha:
PT = P1 + P2 + P3 + P4 + P5 + P6 = 15 + 7, 5 + 15 + 10 + 0,8 + 3, 2 = 51, 5 W
valore che corrisponde, salvo l’approssimazione sull’ultima cifra, alla potenza utile.
Esercitazioni
Esercizio 2
000-000 M6.qxp
27-09-2012
10:05
4
Pagina 4
Modulo A • Grandezze elettriche fondamentali e loro legami, bipoli elettrici
Esercitazioni
Esercizio 3
Per il circuito di figura A2.6 calcolare la corrente I, i rendimenti dei bipoli attivi e le correnti I1 e I2.
I
I01
I1
I2
R1
R2
I01 = I02 = 0,5 A
R1 = 100 Ω
I02
R2 = 80 Ω
R3 = R4 = 160 Ω
R4
R3
Figura A2.6
Esercizio svolto 3.
Soluzione
Trasformando i bipoli attivi di corrente negli equivalenti bipoli attivi di tensione, si ottiene lo schema di figura
A2.7, per il quale si ha:
E2 = R2 I02 = 80 × 0, 5 = 40 V
E1 = R1 I01 = 100 × 0, 5 = 50 V
Essendo E1 > E2 la corrente I ha effettivamente il verso indicato sullo schema; il bipolo attivo E1-R1 si comporta da generatore, mentre il bipolo attivo E2-R2 funziona da utilizzatore attivo.
I
+
V1
+
V2
E1
E2
R1
R2
R3
R4
Figura A2.7
Esercizio svolto 3. Schema
equivalente dopo la
trasformazione dei bipoli
attivi di corrente.
Applicando il secondo principio di Kirchhoff alla maglia si ricava la corrente I:
− E1 + E2 + R2 I + R4 I + R3 I + R1 I = 0
I=
E1 − E2
50 − 40
=
= 0, 02 A = 20 mA
R1 + R2 + R3 + R4 100 + 80 + 160 + 160
Mediante le equazioni tipiche del generatore e dell’utilizzatore attivo si calcolano le tensioni ai capi dei due
bipoli attivi e i loro rendimenti:
V1 = E1 − R1 I = 50 − 100 × 0, 02 = 48V
η1 =
V1 48
=
= 0, 96
E1 50
V2 = E2 + R2 I = 40 + 80 × 0, 02 = 41, 6V
η2 =
E2
40
=
= 0, 9615
V2 41, 6
000-000 M6.qxp
27-09-2012
10:05
Pagina 5
5
A2 • Bipoli elettrici e loro collegamenti
I1 = I01 − I = 0, 5 − 0, 02 = 0, 48 A
I2 = I02 + I = 0, 5 + 0, 02 = 0, 52 A
Esercizi proposti
Esercizio 4
La rete resistiva di figura A2.8 è formata da otto resistenze uguali, di valore 30 Ω. Calcolare i valori delle resistenze equivalenti viste rispettivamente tra i punti A-B e tra i punti A-C.
R2
R4
A
R7
R6
R3
R1
B
R8
R5
C
D
Figura A2.8
Esercizio proposto 4.
R1 = R2 = R3 = R4 = R5 = R6 = R7 = R8 = 30 Ω
[RAB = 21 Ω; RAC = 16 Ω]
Esercizio 5
Del circuito di figura A2.9 sono note tutte le resistenze e la corrente I6. Calcolare tutte le altre correnti indicate
sullo schema, le tensioni VAC e VBG , la resistenza equivalente del carico e il rendimento del generatore.
I
A
E
I1
I45
R1
R4
I6
+
E
Ri = 5 Ω
R1 = 40 Ω
R2 = R3 = 50 Ω
B
R6
G
Ri
C
R2
R3
I2
I3
D
R5
F
R4 = 30 Ω
R5 = 50 Ω
R6 = 100 Ω
I6 = 0,5 A
Figura A2.9
Esercizio proposto 5.
[I = 1,894 A; I1 = 0,769 A; I2 = I3 = 0,3845 A; I45 = 0,625 A; VCA = 50 V;
VBG = –12 V; Req = 26,4 Ω; η = 0,841]
Esercitazioni
Applicando il primo principio di Kirchhoff si determinano le correnti nei due resistori R1 e R2:
000-000 M6.qxp
27-09-2012
10:05
Esercitazioni
6
Pagina 6
Modulo A • Grandezze elettriche fondamentali e loro legami, bipoli elettrici
Esercizio 6
I1
R1
R3
I3
R5
V = 20 V
I56
P1 = 10 W
I2
α
I4
β
R2
V
P2 = 30 W
γ
R6
R4
P3 = 20 W
P4 = 20 W
P5 = 10 W
P6 = 10 W
Figura A2.10
Esercizio proposto 6.
Conoscendo le potenze assorbite dai vari resistori e la tensione totale V del circuito di figura A2.10, calcolare i
valori delle resistenze e delle intensità di corrente.
[R1 = 0,4 Ω; R2 = 10,8 Ω; R3 = 1,8 Ω; R4 = 7,2 Ω; R5 = R6 = 3,61 Ω; I1 = 5 A;
I2 = 1,67 A; I3 = 3,33 A; I4 = 1,67 A; I56 = 1,66 A]
Esercizio 7
Per il circuito di figura A2.11 calcolare le correnti nei vari lati, la corrente impressa, le potenze e il rendimento
del generatore reale di corrente.
I1
I56
B
VBD = 12 V
I2
R1 = 1 kΩ
R2 = 0,5 kΩ
R5
R2
R1
A
R3 = R4 = 1 kΩ
R5 = 0,3 kΩ R6 = 0,7 kΩ
C
Ri = 0,5 kΩ
I0
Figura A2.11
Esercizio proposto 7.
Ri
R3
R4
I3
I4
R6
D
[I1 = 24 mA; I2 = 12 mA; I3 = I4 = 6 mA; I56 = 12 mA; I0 = 96 mA;
Pg = 3,456 W; Pu = 0,864 W; Pp = 2,592 W; η = 0,25]