MODELLO DEL DIODO

MODELLO DEL DIODO
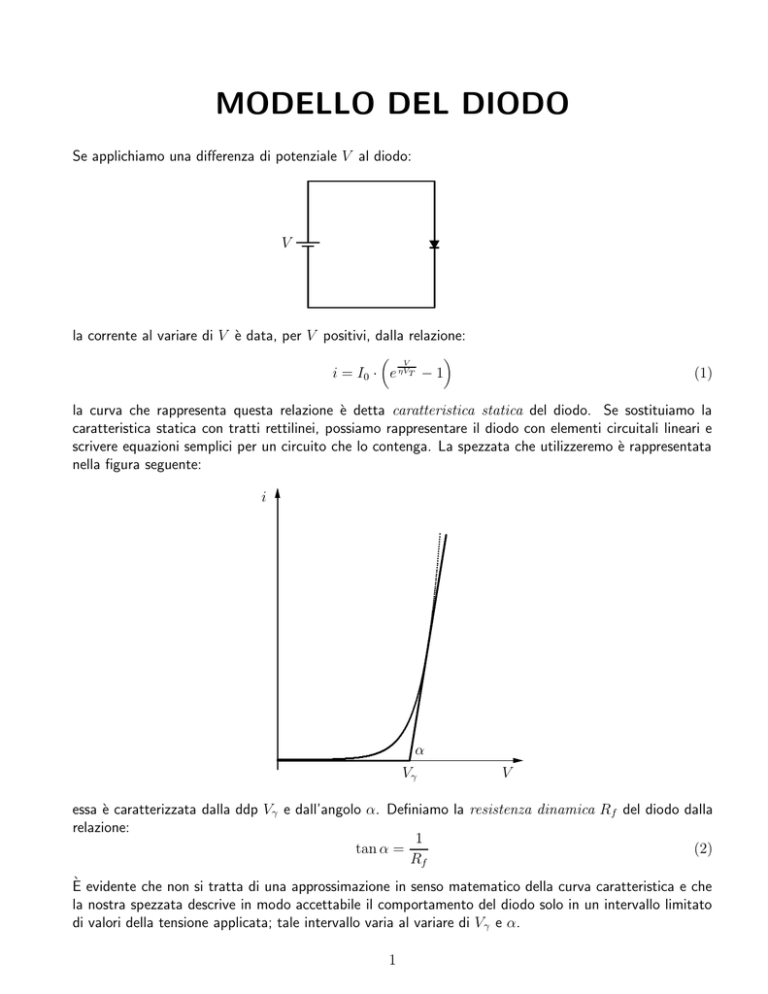
Se applichiamo una differenza di potenziale V al diodo:
V
la corrente al variare di V è data, per V positivi, dalla relazione:
i = I0 · e
V
ηVT
−1
(1)
la curva che rappresenta questa relazione è detta caratteristica statica del diodo. Se sostituiamo la
caratteristica statica con tratti rettilinei, possiamo rappresentare il diodo con elementi circuitali lineari e
scrivere equazioni semplici per un circuito che lo contenga. La spezzata che utilizzeremo è rappresentata
nella figura seguente:
i
··
···
··
···
··
···
··
···
··
···
··
···
··
···
··
····
··
····· α
·
·
·
·
·
·
·
·
··························································
Vγ
V
essa è caratterizzata dalla ddp Vγ e dall’angolo α. Definiamo la resistenza dinamica Rf del diodo dalla
relazione:
1
tan α =
(2)
Rf
È evidente che non si tratta di una approssimazione in senso matematico della curva caratteristica e che
la nostra spezzata descrive in modo accettabile il comportamento del diodo solo in un intervallo limitato
di valori della tensione applicata; tale intervallo varia al variare di V γ e α.
1
Il tratto orizzontale della spezzata rappresenta un circuito aperto (corrente nulla per qualunque valore
della tensione applicata); o, se preferite, è la curva caratteristica di una resistenza infinita. Per il tratto
inclinato abbiamo invece:
1
i = (V − Vγ ) ·
(3)
Rf
che è l’equazione del circuito seguente:
Vγ
V
Rf
nel nostro modello, che potremmo chiamare lineare a tratti, il diodo viene dunque rappresentato nel modo
seguente:
≡
R=∞
V < Vγ
Vγ
V > Vγ
≡
Rf
Il caso estremo di questo modello, quello in cui Rf = 0 e la linea obliqua diventa verticale, costituisce un
modello ancor più semplificato, in cui il diodo viene rappresentato da una resistenza infinita per V < V γ
e da un generatore ideale di ddp Vγ per V > Vγ .
2
1
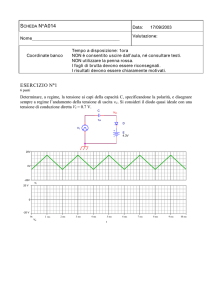
Un esempio: limitatore di tensione
Dato un generatore di tensione alternata Vin possiamo, mediante un diodo ed un generatore in continua
VR , limitare verso l’alto la tensione in uscita Vout utilizzando il seguente circuito:
R
+
Vin (t)
Vout (t)
VR
−
Per calcolare Vout utilizziamo il modello lineare a tratti: nel tratto orizzontale il diodo equivale a una
resistenza infinita e nel ramo che lo contiene non passa corrente, quindi V out = Vin , ossia la tensione di
input si trasferice completamente sull’output. Questo si verifica per V in − VR < Vγ :
Vout = Vin
per
Vin < VR + Vγ
(4)
Per Vin − VR > Vγ , cioè nel tratto obliquo, sostituiamo il diodo col modello visto in precedenza:
+
R
Vγ
Rf
Vin (t)
Vout (t)
VR
−
per questo circuito possiamo scrivere:
Vout = Vγ + VR + Rf i = Vγ + VR +
Rf
(Vin − Vγ − VR )
R + Rf
3
per
Vin > VR + Vγ
(5)
da questa equazione si verifica facilmente che Vout è minore di Vin . Per descrivere ciò che succede,
Rf
possiamo dire che la parte di Vin che eccede Vγ + VR viene ridotta sull’output di un fattore R+R
.
f
La figura seguente mostra l’andamento di Vin e Vout per
Rf
R+Rf
= 0.3.
V
Vin
········
··············
·············
···· ······
·
·· ·· ooooooooooooooo ·····
····· oooooooooooooooo ·····
·
·ooooooooooooo oooooooooooooooooo·oo·oo·
··ooooooooooooooooooooooooooooooooooooooooooo····
·ooooooooooooooo oooooooooooooooooo·o·oo·o
VR +Vγ
o
·oo·oo·
o
·oo·oooo·oooooo
o
·oo·oo·o
·oo·oooo·oooooo Vout ooooooo·oo·oo·oo·o
o
·oo·ooo·ooooo
o
o
·o·oo·o
o
·oo·oo·
o
o
·o·oo·o
o
o
·ooo·o
o
·ooo·o
o
·ooo·o
o
o
o
o
o
·o·oo·
o
o
·oo·oo·
o
o
o
·
o
·
o
o
·
o
o
o
·
o
o
o
·oo·ooooo·o
o
o
·
o
o
·
o
·ooo·o·
o
o
o
o
·o·oo·
o
o
o
·
o
·
o
o
o
o
o
·
o
·
·oo·oo
o
o
o
o
·ooo·o·
o
o
o
o
·o·oo·
o
o
·
o
·
o
o
o
o
o
·
·o·ooo
o
o
·
o
o
o
·
-o·o-------------------------------------------------------------oo·-o·o-o·oo-o·------------------------------------------------------------oo·-oo·-ooo·-o------------------------------------------------------------ooo·-o·o-o·oo-·-----------------------------------------------------------o-o·o-o·o-oo·o------------------------------------------------------------------------------------------------ t
o
o
o
o
·oo·oo·
o
o
·
·
o
·
o
o
·ooo·o·
o
·oo
o
o
·oo·oo·
o
·ooo·o
o
o
o
o
·ooo·o·
·oooo·o
o
o
·
o
o
o
o
o
o
·oo·oo·
o
·
o
·
o
o
·ooo·o·o
o
·oo
o
o
o
·oo·ooo·
o
·ooo·o
o
o
·ooo·o·
·ooo·o
oo
o
o
·oo·oo·o
·o·oooo·o
o
o
·
o
o
·oo·o·
o
·o
o
o
·oo·o·o
·o
oo
oo
·oo·o·o
·oo·o
·
o
oo
ooo
·oo·oo·
o
·
o
·
o
o
·oo·oo·o
oo
·oo·oo·oo·o oo·ooo·ooo·o·o
o
·oo·oo·oo·oo·o o·oooo·o·ooo·oo·o·o
o
·oo·oo·oo·oo·oo·oo·oo·oo·oo·oo·
o
·oo·oo·oo·oo·oo·o
Mentre nel caso estremo Rf = 0 abbiamo:
V
Vin
·············
·············
················
····· ·····
·· ·· ·····
···
·····
·
·
·oo·oooooooooooooooooooooooooooooooooooooooooooooooooo·oo·oo·oo·o·o
·ooo·oooooooooooooooooooooooooooooooooooooooooooooooooo·o·oo·oo·oo·
o
VR +Vγ
oo
·ooo·ooooooooooooooooooooooooooooooooooooooooooooooooooooooo·oo·oo·oo·oo·
o
·
o
oo
o
o
o
·oo·oo·
·oo·ooooo·o
o
o
·
o
·
o
o
·o
·o·oo·o
o
·oo Vout oo·oo·oo·oo·o
o
o
oo
o
o
o
o
·oo·oo·
·
o
·
o
oo
o
·oo·oo·
o
o
o
·
·oo·ooooo·o
o
o
o
·
o
·
o
o
·oo·oo·
o
·oo·oo·
o
·oo
o
o
·oooo·o
o
o
o
o
o
·oo·oo·
o
o
·oo·oo·
·oo·oooo·o
o
o
·
·oo·oooo·o
o
·oo
o
o
o
o
o
·oo·oo·
o
·
o
·oo·oo·
·o·ooo
o
·oo·oo
o
-o·o--------------------------------------------------------------o-o·oo-·o------------------------------------------------------------oo·-oo·-o-------------------------------------------------------------o-o·o-o·oo-·-----------------------------------------------------------o-o·o-oo·o-o·o------------------------------------------------------------------------------------------------ t
o
o
·oo·oo·
o
o
·o
·oo·oo·
o
o
·oo·o
o
o
o
o
o
·oo·oo·
·ooo·o
o
o
o
·
·
o
o
o
o
o
o
·
o
·
o
o
·
o
o
·o·oo·
o
o
·oo·oo·
·ooo·o
o
·ooo·o
o
o
o
oo
o
·o·oo·o
o
o
o
o
·oo·oo·
o
·
o
·
o
o
o
o
o
·
o
·
o
o
o
o
·o·oo·
o
o
·oo·oo·
o
·ooo·o
·oo·o
o
o
o
·o·oo·
·oo·oo·
oo
oo
o
·
o
·
o
o
o
·
o
·
oo
o
·o·oo·o
·oo·oo·o
o
oo
o
·oo·oo·oo· oooo·o·oo·ooo·
o
·oo·oo·oo· o·ooo·ooo·o·oo·
·
o
o
oo
o
o
·
o
·
o
·
·oo·oo·oo·oo·oo·oo·oo·oo·oo·oo
oo
·oo·oo·oo·oo·oo·oo·oo·oo·ooo
Invertendo le polarità del generatore VR e/o del diodo possiamo ottenere limitazioni verso l’alto o verso il
basso, per valori positivi o negativi di Vin (esercizio). Infine, inserendo due rami diodo-generatore con le
polarità del diodo opposte possiamo ottenere la limitazione verso l’alto e verso il basso.
4