CENNI DI OTTICA INTEGRATA
L'ottica integrata è nata nel 1969 presso i laboratori della Bell. Il principio di
funzionamento della guide ottiche, su cui si basa tutta l'ottica integrata, era noto da
tempo tuttavia non aveva avuto applicazione per l'assenza di sorgenti luminose
adatte. La sorgente luminosa è stata inizialmente il laser ad He-Ne e successivamente
il laser a semiconduttore, notoriamente molto più efficiente e compatto al punto da
potere essere, in certi casi, integrato nello stesso circuito ottico.
Lo sviluppo dell'ottica integrata è stato stimolato dal contemporaneo sviluppo delle
fibre ottiche. Le comunicazioni in fibra ottica oggi sono preferite a quelle in cavo
coassiale per la minore attenuazione e la maggiore velocità di trasmissione dei
segnali.
Il circuito ottico è più vantaggioso del circuito elettronico non tanto perché il segnale
ottico è più veloce di quello elettrico (su piccole distanze, quali quelle dei circuiti
integrati ottici, la differenza in genere è irrilevante) quanto per il fatto che, per le
dimensioni micrometriche ottenibili, è possibile mettere a punto dispositivi basati
sull'interazione dei campi elettromagnetici, irrealizzabili con l'ottica convenzionale.
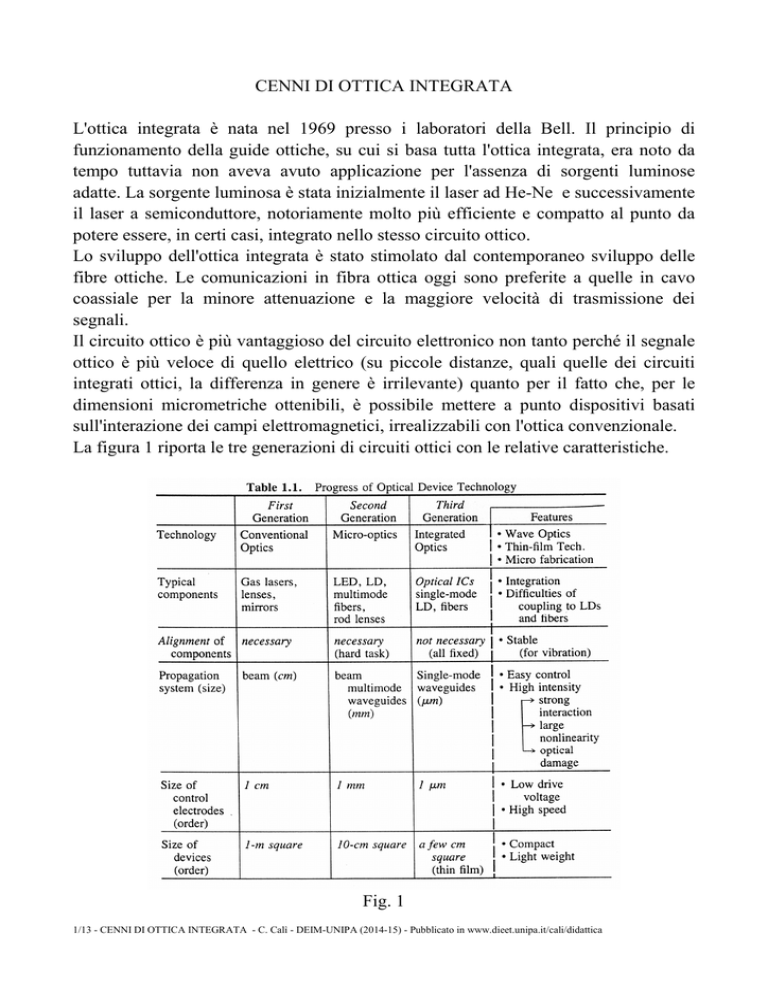
La figura 1 riporta le tre generazioni di circuiti ottici con le relative caratteristiche.
Fig. 1
1/13 - CENNI DI OTTICA INTEGRATA - C. Calì - DEIM-UNIPA (2014-15) - Pubblicato in www.dieet.unipa.it/cali/didattica
Guide ottiche planari
La guida ottica planare è costituita da uno stato sottile dielettrico di indice di
rifrazione nf posto fra un substrato di indice di rifrazione ns e uno strato coprente
(cladding layer) di indice di rifrazione nc (Fig. 2a).
Si osservi che la radiazione è confinata soltanto lungo la direzione x mentre è libera
di propagarsi sul piano yz; questo è il motivo per cui la guida è detta "planare".
Quando invece la radiazione è confinata anche sul piano yz la guida è detta "a
canale".
Fig. 2
L'indice di rifrazione della guida può essere uniforme e quindi aversi una
discontinuità nel passaggio dal substrato alla guida, come indicato in figura 2b,
oppure variabile gradualmente nel passaggio dal substrato alla guida, come in figura
2c. Nel caso di figura 2b la guida è detta del tipo con "indice a gradino" (step-index
type) mentre nel caso di figura 2c è detta del tipo con "indice graduale" (graded-index
type).
Affinché lo strato di indice di rifrazione nf possa guidare la radiazione luminosa è
necessario che il suo di indice di rifrazione nf sia superiore a quello dello strato
coprente così come a quello del substrato. Infatti soltanto in questa caso si può
verificare la situazione di riflessione interna totale e quindi l'effettivo confinamento
della radiazione luminosa.
Spesso l'aria funge da strato coprente e comunque, tranne casi molto particolari,
l'indice di rifrazione dello strato coprente è inferiore a quello del substrato.
Le condizioni sugli indici di rifrazione, ossia nf > nc e nf > ns sono necessarie ma non
sufficienti alla propagazione della radiazione guidata. E' necessario che lo spessore T
della guida sia superiore ad un certo valore, come sarà chiarito più avanti.
2/13 - CENNI DI OTTICA INTEGRATA - C. Calì - DEIM-UNIPA (2014-15) - Pubblicato in www.dieet.unipa.it/cali/didattica
Guide ottiche planari con indice a gradino.
La propagazione della radiazione all'interno della guida rappresentata in figura 2b
può essere spiegata, in modo semplice e intuitivo, mediante l'ottica geometrica, ossia
analizzando il comportamento di un raggio luminoso immesso in qualche modo
all'interno della guida, con un'inclinazione tale da formare un angolo θ rispetto alla
normale alle superfici di discontinuità della guida.
Affinché il raggio venga completamente riflesso nell'incidere sulle superfici di
discontinuità (Fig. 3a) è necessario che l'angolo θ sia superiore, o al limite uguale, al
maggiore dei due angoli critici:
θc = sin-1(nc/nf)
(1)
-1
θs = sin (ns/nf)
(2)
Come già detto, normalmente l'indice di rifrazione del substrato è maggiore di quello
dello strato coprente, di conseguenza, affinché si abbia propagazione guidata, è
necessario che:
θs < θ < 90°
(3)
Qualora questo non dovesse verificarsi si avrebbe perdita di parte della radiazione
verso lo strato coprente e/o verso il substrato, come mostrato in figura 3b e 3c dove si
è supposto che ns > nc.
Fig. 3
3/13 - CENNI DI OTTICA INTEGRATA - C. Calì - DEIM-UNIPA (2014-15) - Pubblicato in www.dieet.unipa.it/cali/didattica
La costante di fase nella direzione di propagazione z è la componente lungo questa
direzione della costante di fase nel dielettrico di indice di rifrazione nf, ossia:
kz = k0 nf sinθ = k0 N,
dove
N = nf sinθ
(4)
prende il nome di "indice di rifrazione effettivo" della guida.
Dalla precedente condizione (3) con la (2) e per la (3) si trova che affinché i raggi
siano confinati dalla guida è necessario che:
ns < N < nf
(5)
Inoltre, affinché si abbia propagazione lungo la guida è necessario che lo spessore T
della guida soddisfi la condizione di risonanza trasversale, ossia lungo la direzione x.
La risonanza si ottiene quando il ritardo di fase in un percorso completo è pari a 2π o
ad un suo multiplo.
Nel computo del ritardo di fase del raggio luminoso lungo la direzione x si deve
considerare lo sfasamento dovuto alle superfici di discontinuità guida-substrato e
guida-strato coprente in presenza di riflessione interna totale.
Per le equazioni di Maxwell nei dielettrici isotropi, privi di perdite ed in assenza di
cariche e nell’ipotesi in cui la propagazione sia lungo l’asse z , per la propagazione
TE si ha l'equazione:
∂ 2E y
− k 02 N 2 − n 2 E y = 0
2
∂x
Le soluzioni di questa equazioni dipendono dalla differenza N2-n2. Precisamente, se
la differenza N2-n2 è negativa la soluzione è di tipo sinusoidale, viceversa la
soluzione è di tipo esponenziale decrescente, ossia si è in presenza di un "campo
evanescente".
Nel caso delle guide planari la soluzione è di tipo esponenziale nel substrato e nello
strato coprente mentre è sinusoidale (o cosinuisoidale) nello strato guidante.
Avendo posto l’origine dell’asse x sulla superficie di discontinuità strato guidante strato coprente diretto verso lo strato coprente e lo spessore dello strato guidante pari
a T (Fig.2b), le soluzioni per la propagazione di tipo TE sono:
(
E y = E c e − γcx
)
per x>0
E y = E f cos(k x x + φ c )
per -T<x<0
E y = E s e γ s ( x +T )
per x< -T
dove, per la continuità dei campi Ey e Hz nell'interfaccia guida - strato coprente:
φ c = tan −1 γ c k x
4/13 - CENNI DI OTTICA INTEGRATA - C. Calì - DEIM-UNIPA (2014-15) - Pubblicato in www.dieet.unipa.it/cali/didattica
La figura 4 rappresenta la distribuzione del campo elettrico per i modi di ordine 0, 1 e
2, nell'ipotesi in cui ns > nc.
Fig. 4
Si osservi che lo sconfinamento della radiazione è maggiore verso il substrato, dove il
salto di indice di rifrazione è minore, ed aumenta con l'aumentare dell'ordine del
modo. Inoltre è possibile dimostrare che lo sconfinamento della radiazione è
maggiore per i modi TM, a parità di ordine del modo e delle caratteristiche delle
guide.
A causa dello sconfinamento menzionato, la sostituzione del substrato o dello strato
coprente con un metallo sarebbe causa di attenuazione della radiazione luminosa.
Qualora fosse necessario porre in prossimità della guida un metallo, ad esempio per
realizzare un elettrodo, dovrà essere interposto uno strato dielettrico di indice di
rifrazione nb più basso di quello dello strato guidante (buffer layer), come
rappresentato in figura 5.
Fig. 5
Guide ottiche planari con indice graduale.
La propagazione della radiazione all'interno della guida planare con indice di
rifrazione graduale, rappresentata nella figura 2c, può essere ancora spiegata
mediante l'ottica geometrica immaginando di suddividere la guida in tanti strati,
5/13 - CENNI DI OTTICA INTEGRATA - C. Calì - DEIM-UNIPA (2014-15) - Pubblicato in www.dieet.unipa.it/cali/didattica
ciascuno di indice di rifrazione decrescente con l'aumentare della profondità x, ed
applicando la legge della rifrazione ad ogni discontinuità.
Guide ottiche a canale
Il vantaggio delle guide a canale consiste nel confinamento della radiazione anche
lungo la direzione y e quindi un fascio stretto, nel propagarsi, non si allarga per
diffrazione come invece avviene nelle guide planari. A parte questo, una guida a
canale, opportunamente progettata, è in grado di deviare il percorso di un fascio
luminoso o ripartire la potenza su più canali, come si vedrà più avanti. Il
confinamento della radiazione luminosa è ottenuto facendo in modo che nella zona
limitrofa alla guida l'indice di rifrazione effettivo sia minore di quello della guida.
Fig. 6
La figura 6 riporta vari tipi di guida a canale. A parte la situazione ovvia della figura
6a, l'aumento dell'indice di rifrazione effettivo della guida è ottenuto, nella 6b
aumentando lo spessore, nella 6c sovrapponendo un dielettrico sulla guida o un
metallo ai margini (l'effetto del metallo è la riduzione dell'indice di rifrazione), nella
6d mediante un campo elettrico (se la guida è elettroottica); in questa ultima figura si
osservi la presenza dello strato di isolamento ottico (buffer).
Tutte le guide a canale possono essere ricondotte ad una struttura generale avente la
forma di un parallelepipedo di sezione rettangolare di lunghezza indefinita.
Per la teoria dei campi elettromagnetici derivante dalle equazioni di Maxwell, le
guide rettangolari a pareti metalliche (ideali) ammettono modi TE e TM. Le guide
ottiche a pareti dielettriche ammettono invece la propagazione di modi "ibridi", ossia
sono "quasi TEM" poiché si ha sia una componente trasversale elettrica sia una
magnetica, con prevalenza di una o di un'altra. Se il campo elettrico è predominante
nella direzione x si dice che l'onda è di tipo x e si indica con Expq, viceversa per la
6/13 - CENNI DI OTTICA INTEGRATA - C. Calì - DEIM-UNIPA (2014-15) - Pubblicato in www.dieet.unipa.it/cali/didattica
direzione y e si indica con Eypq. Le quantità p e q rappresentano l'ordine del modo
nelle direzioni x ed y, così come visto nelle guide planari. Se l'onda ha il campo
elettrico predominante lungo x allora il campo magnetico sarà predominante lungo y
e di conseguenza l'onda è approssimativamente di tipo TM. Viceversa è di tipo TE.
Quindi, riassumendo, Expq→TM, Eypq→TE.
La guida a canale può essere trattata come l'intersezione di due guide planari (sia con
indice di rifrazione a gradino sia graduale), una il cui spessore è lungo la direzione x,
l'altra lungo la direzione y; quindi è pure prevedibile l'andamento dei campi:
sinusoidali all'interno della guida, esponenziali decrescenti all'esterno. La figura 7
rappresenta quanto detto.
Fig. 7
Trasferimento della radiazione luminosa nella e dalla guida ottica
L'efficiente trasferimento della radiazione luminosa rappresenta un problema di una
certa complessità dato che le dimensioni delle guide sono dell'ordine di alcuni
micron.
Il modo più intuitivo per trasferire la radiazione nella/dalla guida è l'accoppiamento
diretto che consiste nell'utilizzare le estremità della guida; queste estremità devono
essere perfettamente piane e ortogonali al piano del substrato. Inoltre, nel
funzionamento in ingresso si deve avere una forte focalizzazione con conseguente
ampio campo angolare dei "raggi", dei quali solo alcuni soddisfano la condizione di
risonanza all'interno della guida. Infine, in presenza di guida multimodale, si avrebbe
l'immissione contemporanea di tutti i modi. Nel funzionamento in uscita, a causa
delle dimensioni delle guide, si avrebbe una elevata diffrazione.
Fig. 8
7/13 - CENNI DI OTTICA INTEGRATA - C. Calì - DEIM-UNIPA (2014-15) - Pubblicato in www.dieet.unipa.it/cali/didattica
Soltanto utilizzando fibre ottiche monomodali (Fig.8a), il cui nucleo guidante è di
pochi micron, o laser a semiconduttore (Fig. 8b), posti a contatto delle facce delle
guide, è possibile ottenere una buona efficienza; comunque è molto critico
l'allineamento della fibra o del laser sulla faccia della guida e rimane la difficoltà di
lavorare otticamente le estremità delle guide.
Un modo più efficiente e selettivo è quello di utilizzare un accoppiatore a prisma,
rappresentato in figura 9 nel funzionamento in ingresso e in figura 10 nel
funzionamento in uscita.
Fig. 9
Fig.10
Si osservi che fra il prisma e la guida è presente un piccolo (ordine delle frazioni di
micron) intercapedine di aria. Nel funzionamento in ingresso l'angolo di incidenza θ e
l'indice di rifrazione np del prisma sono tali che si avrebbe riflessione interna totale in
assenza di guida sottostante. Tuttavia, a causa della piccola distanza fra prisma e
guida si verifica un trasferimento di energia a causa della presenza dei campi
evanescenti presenti all'esterno del prisma. Il fascio deve essere abbastanza largo per
avere fronti d'onda equifase piani e deve essere posizionato in prossimità dello
spigolo del prisma per evitare che la radiazione luminosa rientri nello stesso prisma.
Agendo sull'angolo θ', da cui dipende θ, è possibile immettere selettivamente un
modo anziché un altro. Infatti l'angolo deve essere tale che all'interno della guida i
raggi soddisfino la condizione di risonanza, che equivale a fare in modo che la
velocità di fase nel prisma e nella guida siano uguali.
Analogo è il funzionamento in uscita, ossia le onde evanescenti dei modi che
viaggiano nella guida trasferiscono l'energia luminosa al prisma. Qualora nella guida
viaggiano più modi, questi escono dal prisma con angoli differenti. Nella figura 12b
si osserva il raggio luminoso all'interno della guida che trasferisce gradualmente la
sua energia all'esterno tramite il prisma. Analogo comportamento si ha in ingresso. E'
possibile dimostrare che nel funzionamento in ingresso, in presenza di superfici di
discontinuità piane, l'efficienza massima è dell' 86%, mentre in uscita del 100%.
I vantaggi di questo dispositivo sono che si evita di trattare le estremità delle guide,
consente di immettere un solo modo, è facilmente posizionabile sulla guida ed è
trasferibile da una guida ad un'altra. Questo dispositivo presenta l'inconveniente di
8/13 - CENNI DI OTTICA INTEGRATA - C. Calì - DEIM-UNIPA (2014-15) - Pubblicato in www.dieet.unipa.it/cali/didattica
essere difficilmente integrabile, poco stabile a causa dell'aleatorietà dell'intercapedine
di aria realizzato in genere per semplice pressione sfruttando le piccolissime
imperfezioni delle superfici e abbastanza costoso per la presenza del prisma che deve
essere ben lavorato e realizzato con un dielettrico di indice di rifrazione superiore a
quello della guida.
Un altro modo, sempre selettivo ed efficace, per immettere e prelevare radiazione in
una guida è quello di utilizzare un accoppiatore a reticolo ottenuto realizzando sulla
guida un reticolo di diffrazione. Per effetto del reticolo si generano delle "armoniche
spaziali" e la velocità di fase, che nella guida priva di reticolo è β0 = k0N, assume
valori dati da βq = β0 + q 2π/Λ, dove Λ è il passo del reticolo e q = 0, ±1, ±2, ... Nel
funzionamento in uscita, se si verifica che βq < k0 nc e/o βq < k0 ns allora la radiazione
sfugge dalla guida con un angolo θq che deve soddisfare la relazione:
βq = k0 nc sin θq(c) o/e βq = k0 ns sin θq(s)
ossia che la costante di propagazione nella guida deve essere uguale alla costante di
propagazione nello strato coprente o/e nel substrato. Questo è rappresentato
graficamente in figura 11 per due differenti passi del reticolo.
Fig. 11
Un funzionamento duale si ha in ingresso. I vantaggi di questo tipo di accoppiatore,
oltre alla selettività e all'efficienza comuni all'accoppiatore a prisma, la stabilità,
l'integrabilità e il basso costo se prodotto in larga serie. Gli svantaggi sono la non
trasportabilità da una guida ad un'altra e l'impossibilità di aggiustamenti, ossia il
reticolo, una volta costruito, non lo si può rimuovere o modificare.
I dispositivi ottici integrati possono essere divisi in tre categorie: passivi, funzionali
ed attivi. I dispositivi passivi sono quelli che modificano le caratteristiche della
propagazione all'interno della guida senza l'intervento di agenti esterni; i dispositivi
funzionali necessitano invece di un agente esterno; i dispositivi attivi operano una
conversione di frequenza dell'energia come l'oscillatore laser e il fotodiodo.
9/13 - CENNI DI OTTICA INTEGRATA - C. Calì - DEIM-UNIPA (2014-15) - Pubblicato in www.dieet.unipa.it/cali/didattica
Dispositivi passivi ottici integrati
Dispositivi adatti a ripartire la radiazione luminosa
La guida ramificata, rappresentata in figura 12, ha la funzione di ripartire la potenza
in ingresso sui due rami A e B. La larghezza della guida, dimensionata in modo
supportare il solo modo fondamentale, deve aumentare gradualmente affinché non si
inneschino modi di ordine superiore, la cui propagazione è consentita dalla nuova
dimensione della guida; inoltre l'angolo θ deve essere piccolo (non più di un grado)
per evitare perdita di radiazione (verso il substrato) in prossimità dello spigolo.
Fig. 12
Fig. 13
La figura 13 rappresenta il funzionamento inverso dello stesso dispositivo della figura
precedente, ossia ha la funzione di combinatore di radiazione in dipendenza dalla
relazione di fase fra le due onde immesse. Si osservi che nella situazione (a) l'onda
entrante eccita i modi "0" e "1" ma quest'ultimo non riesce ad essere guidato nella
zona in cui la larghezza della guida diminuisce e pertanto è perduto; nella situazione
(b) le onde entranti eccitano i modi "0" che si sommano perché in fase e i modi "1"
che si elidono perché in opposizione di fase; nella situazione (c) viceversa i modi di
ordine "0" si elidono perché in opposizione di fase e i modi di ordine "1" si sommano
ma non riescono ad essere guidati nella zona in cui la larghezza della guida
diminuisce e pertanto sono perduti.
La potenza può anche essere ripartita mediante un accoppiatore direzione.
10/13 - CENNI DI OTTICA INTEGRATA - C. Calì - DEIM-UNIPA (2014-15) - Pubblicato in www.dieet.unipa.it/cali/didattica
Fig. 14
Come si può osservare nella figura 14, Inizialmente, ossia sulla sinistra della figura,
le due guide, monomodali, si trovano a distanza tale da non interagire fra loro.
Successivamente, a seguito della doppia curvatura della guida inferiore, le due guide
si trovano ad una distanza tale da interagire fra loro per effetto dei campi evanescenti
(accoppiamento delle guide) e quindi si viene a creare una guida equivalente più larga
nella quale posso viaggiare i modi di ordine 0 e 1. Poiché questi modi viaggiano con
velocità differenti (l'indice effettivo N dipende dall'ordine del modo) al temine della
zona di accoppiamento, dovuto alla doppia curvatura della guida superiore, si ha
un'interferenza dipendente dalla lunghezza della zona di accoppiamento. Nella figura
14 la radiazione entra nel canale superiore e il ritardo di fase è tale da avere
interferenza costruttiva all'ingresso del canale inferiore, quindi totale trasferimento
della radiazione da un canale all'altro. Agendo nella zona di accoppiamento sulla
lunghezza o sull'indice di rifrazione delle guide, che potrebbe essere variato
dall'esterno per via elettroottica è possibile ripartire la potenza fra le due guide o
indirizzarla soltanto su una delle due.
E' da osservare che raggi di curvatura grandi e biforcazioni con angoli piccoli
implicano che i dispositivi sopra descritti, come tanti altri, possono avere dimensioni
delle decine di micron lungo la direzione trasversale alla propagazione della
radiazione ma di parecchi millimetri lungo la direzione di propagazione.
Dispositivi separatori o combinatori di lunghezze d'onda
E' possibile realizzare uno specchio selettivo, ossia in grado di riflettere una sola
lunghezza d'onda mediante un reticolo di diffrazione realizzato sulla stessa guida,
come mostrato in figura 15a. La figura 15b evidenzia il comportamento selettivo del
dispositivo che è detto di tipo collineare a differenza di altri che sono di tipo
coplanare. Si osservi che questa struttura è la stessa adottata nella realizzazione degli
specchi nei laser a semiconduttore del tipo "Distributed Bragg Reflector".
11/13 - CENNI DI OTTICA INTEGRATA - C. Calì - DEIM-UNIPA (2014-15) - Pubblicato in www.dieet.unipa.it/cali/didattica
Fig. 15
Dispositivi funzionali ottici integrati
Modulatore basato sull'interferometro Mach-Zehnder
Questo dispositivo è basato sul ritardo di fase conseguente alla variazione dell'indice
di rifrazione dovuta all'effetto elettrottico (Fig. 16) su uno dei due bracci di un
interferometro; di conseguenza le onde nel ricombinarsi non sono più in fase e si
verifica o una somma parziale o nulla secondo il meccanismo riportato nella
descrizione della figura 13.
Fig. 16
Ovviamente la velocità di risposta del dispositivo basato sull'effetto elettroottico è di
gran lunga superiore.
Qualche esempio di sistema ottico integrato
Analizzatore di spettro di radiofrequenza
Con riferimento alla figura 17, il segnale di radiofrequenza da analizzare è inviato
agli elettrodi di un trasduttore piezoelettrico che genera un'onda acustica superficiale
il cui passo dipende dalla frequenza del segnale; di conseguenza la deflessione di un
fascio luminoso generato da un laser funzionante in continua dipende dalla frequenza
del segnale elettrico.
Fig. 17
12/13 - CENNI DI OTTICA INTEGRATA - C. Calì - DEIM-UNIPA (2014-15) - Pubblicato in www.dieet.unipa.it/cali/didattica
Uno dei fotorivelatori di una schiera intercetta il fascio opportunamente focalizzato e
quindi, dal fotorivelatore illuminato e dal livello di illuminazione si può ottenere
l'informazione sulla frequenza e sulla intensità. Poiché un segnale contenente più
frequenze genera più onde acustiche superficiali contemporaneamente, il sistema è in
grado di dare le informazioni sul contenuto armonico del segnale, così come un
analizzatore di spettro tradizionale.
Sensore di temperatura
Fig. 18
Questo sensore, riportato in figura 18, è costituito da tre interferometri di cui due (A e
B) con rami molto differenti e che differiscono di poco (λ/4Neff) fra loro e uno (C) i
cui rami sono poco differenti. Questi interferometri ricevono l'energia luminosa da
una sorgente costante ed uniformemente ripartita. La radiazione che esce dagli
interferometri e convertita, tramite fotorivelatori non rappresentati in figura, in
segnali elettrici.
Se gli interferometri avessero i rami di eguale lunghezza e uguale sezione, una
variazione di temperatura, che induce una variazione dell'indice di rifrazione
dell'intero substrato, non causerebbe una variazione dell'intensità luminosa presente
alle uscite. Cosa che invece si verifica quando i rami sono differenti e tanto più
quanto lo sono. Per ottenere una elevata risoluzione è opportuno avere interferometri
del tipo A o B, tuttavia, tenendo presente che l'intensità luminosa in uscita varia
periodicamente con la temperatura, la dinamica risulta bassa. Per ottenere una
dinamica maggiore, ma una minore risoluzione, si deve prelevare l'informazione
dall'interferometro C. La piccola, ma calibrata, differenza fra gli interferometri A e B
permette di avere una buona risoluzione anche quando l'intensità di uscita di uno dei
due si trova in una situazione di minimo o di massimo dove la sensibilità assume il
valore minimo. In queste condizioni l'altro interferometro si trova nella condizione di
massima sensibilità, essendo la sua uscita sfasata di λ/4Neff.
Riassumendo, l'insieme dei tre interferometri consente di ottenere una elevata
risoluzione in un campo di temperature grande.
Tutte le figure riportate in queste note sono tratte, in certi casi opportunamente modificate e
corrette, dal testo:H.Nishihara, M.Haruna, T.Suhara: "Optical Integrated Circuits" - McGraw-Hill
13/13 - CENNI DI OTTICA INTEGRATA - C. Calì - DEIM-UNIPA (2014-15) - Pubblicato in www.dieet.unipa.it/cali/didattica












