Modello di Elmore: generalizzazione
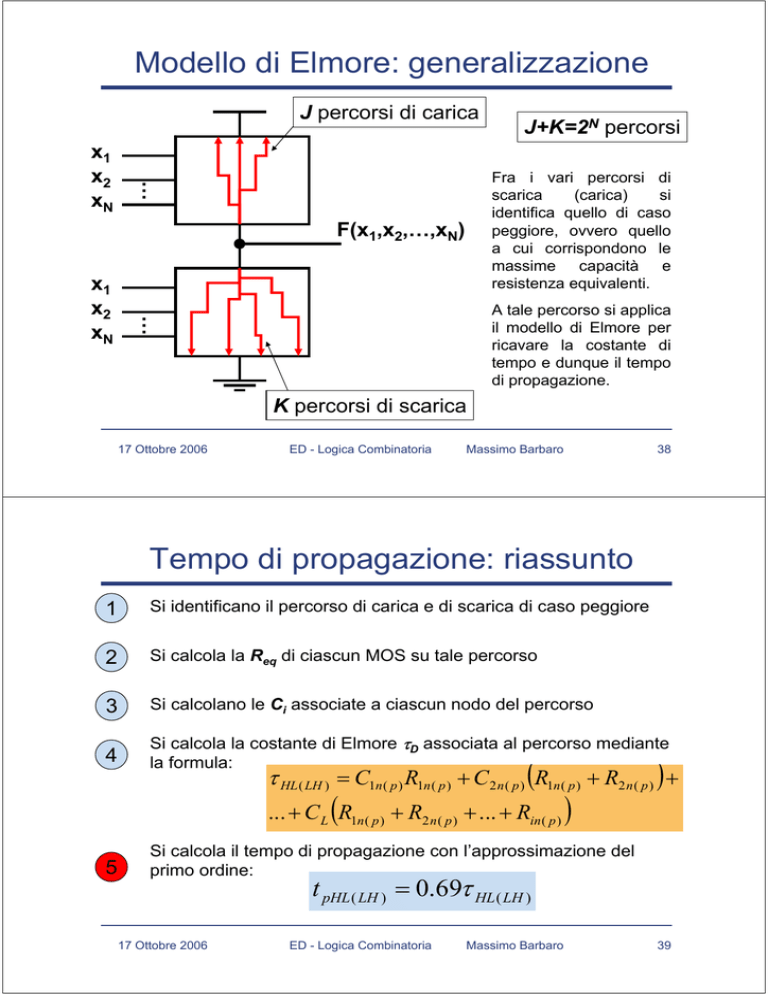
J percorsi di carica
Fra i vari percorsi di
scarica
(carica)
si
identifica quello di caso
peggiore, ovvero quello
a cui corrispondono le
massime capacità e
resistenza equivalenti.
…
x1
x2
xN
F(x1,x2,…,xN)
A tale percorso si applica
il modello di Elmore per
ricavare la costante di
tempo e dunque il tempo
di propagazione.
…
x1
x2
xN
J+K=2N percorsi
K percorsi di scarica
17 Ottobre 2006
ED - Logica Combinatoria
Massimo Barbaro
38
Tempo di propagazione: riassunto
1
Si identificano il percorso di carica e di scarica di caso peggiore
2
Si calcola la Req di ciascun MOS su tale percorso
3
Si calcolano le Ci associate a ciascun nodo del percorso
4
Si calcola la costante di Elmore τD associata al percorso mediante
la formula:
τ HL ( LH ) = C1n ( p ) R1n ( p ) + C2 n ( p ) (R1n ( p ) + R2 n ( p ) ) +
... + C L (R1n ( p ) + R2 n ( p ) + ... + Rin ( p ) )
5
Si calcola il tempo di propagazione con l’approssimazione del
primo ordine:
t pHL ( LH ) = 0.69τ HL ( LH )
17 Ottobre 2006
ED - Logica Combinatoria
Massimo Barbaro
39












