Accelerometri
Accelerometri
Modello di riferimento e similari
Taratura
Tipi e modelli
Usi comuni
Montaggio e precauzioni
Modello di riferimento
y, y& , &y& x, x& , &x&
vibrazione da misurare
m
y, y& , &y& vibrazione della massa inerziale
kel
c
z, z&, &z& vibrazione relativa tra massa inerziale
x, x& , &x&
e guscio del trasduttore
Imponendo l’equilibrio dinamico:
m&y&
kel ( y − x)
z = x− y
m&y& + kel ( y − x) + c( y& − x& ) = 0
⇒ m&z& + cz& + kel z = m&x&
c( y& − x& )
Modello del II ordine
z(t) è l’output del trasduttore, che viene poi
misurato da un trasduttore di spostamento.
Modello di riferimento
~
x(t ) = X ⋅ Sin(ωt ) ⇒ X = X ⋅ exp(iωt )
~
~
x& (t ) = ωX ⋅ Cos(ωt ) ⇒ X& = iω ⋅ X ⋅ exp(iωt ) = iω ⋅ X
~
~
&& = −ω 2 X ⋅ exp(iωt ) = −ω 2 X
x&&(t ) = −ω 2 X ⋅ Sin(ωt ) ⇒ X
~
y (t ) = Y ⋅ Sin(ωt ) ⇒ Y = Y ⋅ exp(iωt )
~
~
y& (t ) = ωY ⋅ Cos(ωt ) ⇒ Y& = iω ⋅ Y ⋅ exp(iωt ) = iω ⋅ Y
~
~
y&&(t ) = −ω 2Y ⋅ Sin(ωt ) ⇒ Y&& = −ω 2Y ⋅ exp(iωt ) = −ω 2Y
~
z(t ) = Z ⋅ Sin(ωt ) ⇒ Z = Z ⋅ exp(iωt )
~
~
z&(t ) = ωZ ⋅ Cos(ωt ) ⇒ Z& = iω ⋅ Z ⋅ exp(iωt ) = iω ⋅ Z
~
~
z&&(t ) = −ω 2Z ⋅ Sin(ωt ) ⇒ Z&& = −ω 2Z ⋅ exp(iωt ) = −ω 2Z
Sostituendo le equazioni complesse in (1)…
Modello di riferimento
m&z& + cz& + kel z = m&x& ⇒ ( − mω 2 + iωc + k el ) ⋅ Z~ = − mω 2 X~
Diverse grandezze possono essere considerate input:
• Spostamento
~
Z
− mω 2
H (iω ) = ~ =
X (k s − mω 2 ) + iωc
Sismometro
• Velocità
~
Z
iωm
H (iω ) = ~ =
iωX (k s − mω 2 ) + iωc
Velocimetro
• Accelerazione
H (iω ) =
~
Z
m
~ = (k − mω 2 ) + iωc
−ω X
s
2
accelerometro
Modello di riferimento
Divido numeratore e denominatore per kel …
m
1
= 2 and
kel ωn
m
2⋅c⋅
k el
c
2⋅c⋅m
2ξ
=
=
=
k el 2 ⋅ k el ⋅ m 2 ⋅ k el ⋅ m ωn
Perciò:
~
Z
− ω 2 / ωn2
H (iω ) = ~ =
X (1 − ω 2 / ωn2 ) + 2iξω / ωn
Sismometro
~
iω / ωn2
Z
H (iω ) = ~ =
iωX (1 − ω 2 / ωn2 ) + 2iξω / ωn
velocimetro
~
Z
1/ ωn2
H (iω ) =
=
2 ~
− ω X (1 − ω 2 / ωn2 ) + 2iξω / ω n
accelerometro
Sismometro
Il misurando è l’oscillazione dell’elemento vibrante.
3
0 .0 0 0 5
0 .2
0 .3
0 .4
0 .5
1
1 .5
2 .5
2
1 .5
1
0 .5
ξ↑
ω /ω
0
0
1
2
3
ω
−
~
Z
ωn
H(iω) = ~ =
2
X ω
ω
1− + 2iξ
ωn
ωn
4
5
2
6
7
2
H(iω) =
ω
ωn
2
2
ω 2
ω
1− +4ξ2
ωn
ωn
8
9
n
10
ω
2ξ
ω
∠H(iω) = n ⋅ π − tan−1 n 2
ω
1−
ωn
Accelerometro
Il misurando è l’accelerazione, la lettura avviene misurando lo
spostamento della massa inerziale
→ accelerometro a deflessione.
Second order instrument: FRF (phase)
Second order instrument: FRF (Module)
0
qo/(Kqi)
6
5
ξ=0
4
3
ξ = 0.1
ξ = 0.2
2
ξ = 0.4
ξ = 0.6
1
ξ = 1.5
ω/ωn
0
0
1
2
3
2
1
~
Z
ωn
H (iω ) = ~ =
2
X ω
ω
1
−
+
2
i
ξ
ωn
ωn
4
5
0
-10
-20
-30
-40
-50
-60
-70
-80
-90
-100
-110
-120
-130
-140
-150
-160
-170
-180
2
1
2
3
4
ω/ωn
5
ξ = 0.1
ξ = 1.5
ξ=0
φ[°]
1
ωn
H ( iω ) =
2 2
2
ω
2 ω
1 − + 4ξ
ωn
ωn
ω
2ξ
ωn
∠H (iω ) = nπ − tan −1
2
ω
1−
ωn
K=m/ks – sensibilità statica
Modello di riferimento
Gli accelerometri a deflessione possono essere realizzati usando diversi principi
di misura per valutare lo spostamento della massa
• Accelerometri a spostamenti relativi: capacitivo, induttivo, potenziometrico
• Accelerometri estensimetrici o piezoresistivi
• Accelerometri piezoelettrici
•Accelerometri MEMS – capacitivi or piezoresistivi
Ad esempio considerando un accelerometro estensimetrico…
Estensimetri
vibrazione da misurare
Forza inerziale sulla massa
m
Deformazione dell’asta
x, x&, x&&
Misura di deformazione (∆R)
Modello di riferimento
Proprietà degli accelerometri a deflessione:
DEFLESSIONE
AZZERAMENTO
RELATIVO
ASSOLUTO
CONTATTO
SENZA CONTATTO
Modello di riferimento
Effetti di carico:
• sulla relazione massa – molla
• sulla frequenza del misurando
F = M ⋅a ⇒ a = F
M
a~ = F
a
m
=
1
+
M
a~
( M + m)
m
a
M
F
K
ωrf =
a~
C
K
M
M
K
ω~rf =
K
M +m
F
C
La massa
dell’accelerometro
dovrebbe essere
piccola se
confrontata con la
massa vibrante
ω rf
= 1+ m
~
M
ω rf
Taratura degli accelerometri
Gli accelerometri sono
solitamente tarati a
1000 rad/s = 159.2 Hz
con ampiezze di 10 m/s2.
Taratura degli accelerometri
Il metodo interferometrico è usato solo per la taratura di standard
primari nazionali, mentre tecniche più pratiche sono usate
comunemente con trasduttori campione:
• Back to back
Vu
amp.
accelerometro
da tarare
amp
Aosinωt
Tavola vibrante
Sensibilità
Accelerometro
campione
Vr
DAQ
au = ar
Vu Vr
=
ku k r
ku = k r ⋅
Vu
Vr
Taratura degli accelerometri
Tipi e modelli di accelerometri
• Accelerometri capacitivi: sensibili ad un cambio nella
capacità elettrica derivante dall’accelerazione.
L’accelerometro misura la variazione di capacità tra una
condizione stazionaria ed una dinamica.
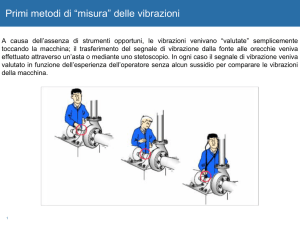
• Piezoaccelerometri: sfruttano materiali come cristalli di
quarzo, che generano potenziale elettrico se viene imposta
una deformazione. L’effetto piezoelettrico consiste nella
ridisposizione di cariche elettriche a causa dello sforzo meccanico.
• Accelerometri piezoresistivi (ed estensimetrici): funzionano
misurando la resistenza elettrica di un materiale che varia
quando questo viene deformato.
• Accelerometri ad effetto Hall Effect: misurano la variazione di
tensione originata da un cambiamento del campo magnetico
attorno all’accelerometro
Tipi e modelli di accelerometri
• Accelerometri Magnetoresistivi: funzionano misurando variazioni di
resistenza elettrica causata da un campo magnetico. La struttura ed il
funzionamento sono analoghi agli accelerometri ad effetto Hall, ma non è
richiesta una misura di tensione, solo di resistenza.
• Accelerometri a trasferimento di calore: misura i cambiamenti interni
di trasmissione termica legati all’accelerazione. Una singola sorgente di
calore è sospesa su una cavità, termistori posti tutt’attorno misurano
asimmetrie geometriche nel trasferimento termico dovuti allo
spostamento della massa calda.
• Micro-Electro Mechanical System (MEMs): tecnologie basate su una
vasta serie di strumenti e metodologie, che sono usate per creare
strutture di dimensioni micrometriche (un millesimo di metro). Queste
tecnologie si rifanno come principio di misura a quanto già visto in
precedenza, ma la loro scala li rende molto facilmente usabili in molti
settori e facili da integrare.
Servoaccelerometri
L’accelerazione è
compensata da una
retroazione che
mantiene la massa
ferma: metodo ad
azzeramento
• alta sensibilità (> 1000 mV/g)
• basse frequenze (0÷500 Hz)
Piezoaccelerometro
• Il parallelo massa molla smorzatore è dato da un prisma
piezoelettrico, con una piccola massa ed una alta rigidezza.
• Normalmente il cristallo è precaricato.
• Nessuno smorzatore aggiunto: smorzamento molto basso (0.3).
High sensitivity
accelerometro
High frequency
accelerometro
Mass 43 g
Mass 0.63 g
Sens.10 pC/(ms-2)
Sens. 0.15 pC/(ms-2)
Freq. 1-4800 Hz
Freq. 1-26000 Hz
Piezoaccelerometro
Il cristallo ha un’alta impedenza, quindi per misurare la
carica è necessario usare un voltmetro ad alta
impedenza, al fine di evitare che la misura stessa causi
la scarica del cristallo. Poichè spesso questo è
impossibile, un preamplificatore è usualmente
collegato tra il trasduttore ed il sistema di acquisizione.
La preamplificazione può avvenire in carica o in tensione.
Solitamente si usano amplificatore di carica oppure
amplificatori di tensione direttamente a bordo del
trasduttore (circuiti a bordo).
L’amplificazione in tensione è da evitare quando si usano
cavi lunghi a causa della resistenza dei cavi.
Piezoaccelerometro
Piezoaccelerometri con circuito a bordo sono disponibili sul mercato con
vari nomi: ICP (trade mark di PCB piezotronics), IEPE (Bruel & Kjaer) e
molti altri. L’acronimo più noto è ICP – Integrated Circuit Piezoelectric.
Piezoaccelerometro
L’amplificazione a bordo ICP/IEPE richiede a sua volta un
condizionatore per fornire l’alimentazione richiesta
Piezoaccelerometro
Three axial ICP
I condizionatori ICP sono compatti, affidabili
ed utili, ma possono presentare problemi in
temperatura, legati alla sensibilità termica del
circuito a bordo
Mono axial ICP
Tipi e modelli di accelerometri
ATTENZIONE: I cristalli piezoelettrici col tempo
riallineano le loro cariche internamente, quindi
misure in bassa frequenza (3-5Hz) non sono possibili
Usi principali
Vibrazione:
Comfort vibrazionale umano
Diagnostica industriale su macchinari
Diagnostica civile su edifici
Accelerazione:
Sistemi di navigazione inerziale
Misura e rilevamento degli impatti
Caratterizzazione dinamica dei materiali
Montaggio e precauzioni
Montaggio e precauzioni
Montaggio e precauzioni
Montaggio e precauzioni