baschieri138877

Nome:ELENA BASCHIERI
N ° matricola:138877
Data:13.12.2001, 0re: 14.00 / 16.00
Il ciclo frigorifero
Attraverso un esercizio relativo al ciclo frigorifero è possibile comprendere quali
sono le grandezze coinvolte in un impianto frigorifero.
Il ciclo è un ciclo classico. Si utilizza come fluido refrigerante il freon 12, un
liquido inserito nei frigoriferi di vecchia maniera , che non gela a temperature
inferiori lo 0. Oggi, per problematiche ambientali, il freon 12 è stato sostituito con
altre tipologie di fluidi aventi caratteristiche simili.
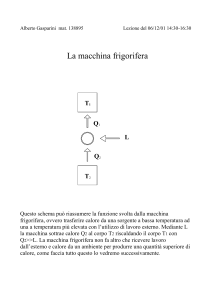
Il diagramma TS (temperatura assoluta in funzione dell’entropia specifica) del
freon 12 è abbastanza simile al diagramma a campana dell’acqua (chiaramente i
valori saranno differenti). Rappresentiamo il diagramma TS:
T
3
2
4
1
S
Per eseguire l’esercizio serviranno le tabelle energetiche relative a questo fluido.
Nel ciclo si avranno:
 compressore
 condensatore
 strozzatore
 evaporatore
Chiamiamo i tratti: 1, 2, 3, 4 e vediamo dal diagramma quello che avviene
nei vari passaggi.
-1-
Data:13.12.2001, 0re: 14.00 / 16.00
3
condensatore
2
valvola di
laminazione
calore
sottratto
compressore
1
4
lavoro speso
evaporatore
Rispettivamente sappiamo che nel passaggio dal punto 1 al punto 2, in cui si ha
il compressore, sarà fornito lavoro al fluido, quindi partendo dal punto 1 sulla curva
limite superiore, si opera una compressione adiabatica reversibile (a entropia
costante) che trasforma il fluido in stato liquido a causa dell’alta pressione a cui è
sottoposto; si salirà così in verticale fino al punto 2. Nel passaggio dal punto 2 al
punto 3 si trova il condensatore, cioè uno scambiatore, costituito da un insieme di
tubi metallici alettati e caratterizzati da una buona conduttività termica,che sottrae
calore al nostro fluido ( qc ). Nel grafico ci saranno due andamenti: uno orizzontale
(all’interno della campana) e uno caratteristico di un’isobara (all’esterno della
campana). A questo punto il fluido viene fatto espandere attraverso una
trasformazione adiabatica che tende a far diminuire la temperatura; ciò consente, a
seguito di un processo di evaporazione, di sottrarre calore all’ambiente che si vuole
refrigerare (passaggio 3 -4). Riportando infine la sostanza operante nelle condizioni
iniziali attraverso un processo isobarico, si può realizzare una successione continua
di cicli di raffreddamento, purché si fornisca energia al sistema.
Supponendo di avere una pressione a monte e a valle del compressore
rispettivamente di 3.6 bar e 9.6 bar e nota la struttura del nostro ciclo, quindi avendo
a disposizione il diagramma del freon, si possono ricavare punto per punto i valori
delle pressioni e soprattutto delle entalpie specifiche del fluido.
Riportiamo in una semplice tabella i valori.
1
2
3
p
3.6 bar
9.6 bar
9.6 bar
t
5 °C
50 °C
40 °C
-2-
H (Kj / Kg)
353.611
371.06
288.53
Data:13.12.2001, 0re: 14.00 / 16.00
4
3.6 bar
5 °C
238.52
Volendo calcolare il rendimento hF , si dovrà calcolare qE , cioè il calore sottratto
dall’evaporatore, e l c , ovvero il lavoro speso dal compressore. Infatti ricordiamo
che:
hF =
qE
lC
Scriviamo dunque le equazioni per il sistema aperto rispettivamente per
l’evaporatore e per il compressore
qE  h1  h4 = 115,085
Kj
K
lC  h2  h1  17,459
Kj
K
Sostituendo i valori trovati si otterrà così
F  6,6
Se vogliamo confrontare il nostro rendimento con quello della macchina ideale
di Carnot ( in cui si considera come temperatura massima quella di evaporazione e
come temperatura minima quella di condensazione) basta sostituire i valori nell’
equazione
C 
tev
278

 7,9
tcon
35
Da ciò è possibile rilevare il fatto che la nostra macchina non è ideale poiché
introduce un ciclo differente da quello di Carnot con un rendimento inferiore rispetto
a quello ideale.
-3-
Data:13.12.2001, 0re: 14.00 / 16.00
Il comfort termoigrometrico
Interessarsi alla questione del “comfort termoigrometrico” significa ricercare in
un ambiente una condizione tale da consentire di avvertire una sensazione di
piacevolezza dal punto di vista fisico.
La prima grandezza che viene in mente e con la quale pensiamo di poter definire
un ambiente è la temperatura; questa però non è sufficiente. Avere una temperatura,
infatti, di 20 °C all’interno di un ambiente non significa necessariamente che questo
sia più o meno confortevole. Se ci troviamo ad esempio in una sauna, per quanto la
temperatura non sia molto alta, la sensazione è di spiacevolezza dal momento che,
essendo l’umidità, contrariamente, molto elevata, percepiamo estremo caldo. Se,
invece, ci troviamo al mare alla stessa temperatura, ma in condizione di brezza e aria
molto secca, la sensazione è di un ambiente piacevole, o addirittura fresco.
Dunque, è possibile intuire come non basti determinare soltanto la temperatura,
ma anche l’umidità.
La casistica è anzi più complessa perché occorre accertarsi della funzione del
locale e conseguentemente dell’ abbigliamento indossato dalle persone che questo
accoglie. Comprendiamo ciò se per esempio paragoniamo una palestra con un
ospedale: nella prima la temperatura può essere più bassa perché facendo attività
fisica il nostro corpo produce calore mentre nel secondo, ove ci sono delle persone
malate e in situazioni disagevoli, con la stessa temperatura si potrebbe addirittura
percepire freddo.
Quindi, solo considerando la funzione del locale, l’attività svolta e l’
abbigliamento tenuto in questo, si potranno stabilire gli intervalli di temperatura e di
umidità che rendono la vita al suo interno sana e piacevole.
E’ certo comunque che non si potrà mai raggiungere una situazione di comfort
totale, ovvero valido per tutti, dal momento che il cambiamento di percezione varia
da persona a persona. Come fece Fanger, uno scienziato danese che ricreò precise
condizioni di caldo e di freddo, usando gli studenti come cavie, e riuscì a stabilire la
temperatura ottimale di un ambiente in relazione all’età, all’attività e
all’abbigliamento (variabile legata a usi e costumi della popolazione), si deve cercare
di riprodurre una situazione piacevole al maggior numero di persone.
Nel difficile compito di raggiungere un comfort termoigrometrico di cui può
beneficiarela maggioranza, sono state ricavate, da teorie più o meno efficaci o
fantasiose, delle tabelle empiriche a rilievi sperimentali che permettono di decidere
in funzione dell’ utilizzo del locale quali devono essere gli intervalli di temperatura e
di umidità entro cui bisogna rimanere per mantenere il locale vivibile.
Questi si basano maggiormente sulla teoria che considera il corpo umano un
sistema aperto, ovvero un sistema che scambia calore con l’ esterno.
-4-
Data:13.12.2001, 0re: 14.00 / 16.00
M  LP  LG  U  ED  ES  ER  VS  R  C
Questa è l’ equazione energetica del nostro sistema aperto in condizione di
equilibrio. E’ con tale scambio che l’organismo può difendersi dal caldo e dal freddo
attraverso la regolazione della sudorazione: se l’ambiente è troppo freddo, infatti, il
nostro corpo disattiva i meccanismi di sudorazione minimizzando lo scambio con
l’esterno e la dispersione di calore, mentre se l’ambiente è troppo caldo aumenterà la
sudorazione.
Definiamo quindi i termini che compaiono nella suddetta equazione:
M: energia prodotta internamente dal metabolismo. Si misura in watt ed è
l’unico positivo nella formula. Altre energie sono negative perché abbandonano
l’organismo per una serie di trasferimenti di energia meccanica e termica.
Lp: energia prodotta dal metabolismo usata per l’attività polmonare, molto
dispendiosa, che cede energia meccanica nell’aria e che è dissipata negli attriti (ex:
naso).
L g: energia usata per svolgere lavoro contro le forze esistenti ( come la forza di
gravità). Si parla di meccanismo dell’erogazione : quando un muscolo eroga energia
brucia O2 , quando rientra nel corpo non viene riconvertita in energia, ma dissipata in
calore che scalda il muscolo.
U: energia accumulata nel nostro organismo.
E d: calore disperso per evaporazione sulla pelle che richiede calore latente di
vaporizzazione. Si parla di evaporazione secca ( come succede ad esempio nel
deserto)
E s : calore disperso per evaporazione del sudore sulla superficie della pelle.
Ed – Es =Ws : identifica la sudorazione massima e minima.
Er - Vs : calore disperso con la respirazione.
R + C = calore scambiato dalla superficie esterna con il nostro corpo mediante
l’irraggiamento e la convezione.
Il metodo di regolazione del nostro organismo è dunque la sudorazione: se un
ambiente quindi è saturo, il nostro sudore non potrà evaporare perché l’aria sarà già
piena di tutto il vapore acqueo disponibile, il nostro meccanismo di regolazione sarà
impedito e dovrà aumentare maggiormente la sudorazione.
Ciò serve a ribadire ulteriormente il concetto che per definire il comfort
dell’ambiente, oltre la temperatura che regola i nostri scambi con questo in termini di
convezione e irraggiamento, conta anche il bilancio dell’umidità relativa perché in
funzione di questa il nostro organismo sarà più o meno facilitato nello scambiare
calore.
Tornando all’esempio della sauna, in cui l’umidità è quasi pari al 100%, si può
capire come qui, non essendo possibile l’evaporazione di un’altra massa liquida e
malgrado ciò sia messo in azione il meccanismo della sudorazione, il sudore che si
trova sulla pelle non possa evaporare e quindi refrigerare l’organismo. Ecco così
spiegata la sensazione di caldo estremo. Contrariamente, al mare, essendoci meno
umidità e più ventilazione, la refrigerazione sarà agevoltata poiché viene asportato
più facilmente il calore.
-5-
Data:13.12.2001, 0re: 14.00 / 16.00
Nella definizione del comfort ambientale è utile avvalersi del DIAGRAMMA
PSICROMETRICO in cui è riportata la temperatura (sull’asse delle ascisse) e il
titolo, ovvero la grandezza che serve a identificare l’umidità dell’aria (sull’asse delle
ordinate).
X
t
0 °C
20 °C 40 °C 60°C 80 °C 100°C
linee a titolo costante
linee a entalpia costante
linee a temperatura costante
DEFINIZIONI
titolo: X 
MV
Kgv

M VS
Kg a
Mv
Pv  Ptot
Vv
n
v
 Ptot v  Ptot
Mv Ma
Vtot
ntot

v
pressioni parziali:
-6-
a
Data:13.12.2001, 0re: 14.00 / 16.00
Ma
Pa  Ptot
Va
n
a
 Ptot a  Ptot
Mv Ma
Vtot
ntot

v
dove a  29Kg / Kmol
v  18Kg / Kmol
M   n
m: massa molare
a
n: n° moli
massa di vapore di saturazione: Mvs
umidità relativa o grado igrometrico
(rapporto tra masse) o (rapporto tra pressioni)

Mv
n
P
 v  v
M vs nvs Pvs
ESERCIZIO
In una situazione di aria umida a una temperatura di 30 °C, umidità del 60 % e
pressione di 1 bar, determinare il titolo X e la pressione parziale del vapore ( pv ).
Per definizione sappiamo che:

Mv
n
 v
M vs nvs
Identificando con Mv e Mvs rispettivamente la massa del vapore e la massa del
vapore in saturazione e con mv, e mvs il numero di moli del vapore e il numero di
moli del vapore in condizione di saturazione.
Poiché il vapor d’ aria e d’ acqua sono assimilabili a un gas perfetto, possiamo
scrivere l’equazione dei gas perfetti:
PvV  v  R0  T
essendo V il volume, R0 la costante universale dei gas e T la temperatura
assoluta. Questa è valida in situazione di non saturazione. Se invece ci si trova in
questa condizione con volume e temperatura uguale si avrà
-7-
Data:13.12.2001, 0re: 14.00 / 16.00
PvsV  vs  R0  T
riscriviamo dunque il rapporto tra moli in termini di pressione, volume e
temperatura:

Pv
da cui Pv    Pvs
P vs
 0,6  0,04241
 2545Pa
Il secondo valore da trovare è il titolo assoluto, avendo umidità relativa:
X 
M v mv  nv
P
P
  Pvs

 0,622 v  0,622 v  0,622
M a ma  na
Pa
P  Pv
P    Pvs
Sostituiamo i valori numerici
X  0,622 
0,025446
 0,0162
1  0,025446
ovvero 16,24
ga
Kg a
ESERCIZIO
Calcolare i valori del flusso in uscita in un miscelatore ove si ha una semplice
miscelazione senza scambio di calore e umidità in cui entrano due flussi d’aria in
condizioni differenti. Sono note la pressione di 1 bar, la portata in massa di aria della
prima e della seconda corrente, rispettivamente pari a M1a = 400 kg / h e M2a = 800
Kg / h, la temperatura del primo e del secondo flusso, pari a t1 = 32 °C e t2 = 26 °C e
le rispettive umidità relative f1= 0.8 e f2 = 0.5.
-8-
Data:13.12.2001, 0re: 14.00 / 16.00
1
3
2
Ciò che richiede il problema è la determinazione del titolo x 3, dell’entalpia J3,
della temperatura t3 e dell’umidità f3 .
Cominciamo a considerare il bilancio in termini di massa e di energia e quindi
con la legge di conservazione della massa andiamo a defini re le varie grandezze in
ingresso e in uscita. Saprò che:
M 3a  M 1a  M 2 a  (400  800) Kg / h  0,33Kg / s
Posso scrivere la medesima equazione per il bilancio in massa del vapore d’
acqua perché so che l’acqua entrerà sotto forma di vapore da a1 e a2 e uscirà da a3
sempre sotto forma di vapore, conservandosi quindi la portata del vapore.
M 3v  M 1v  M 2v
Devo però calcolare i valori dei vapori in ingresso. Sapendo che
X 
M v
M
a
ricavo che
M v  X  M a
riscriviamo l’equazione
X 3 M 3a  X 2 M 2 a  X 1M 1a
Sappiamo che
-9-
Data:13.12.2001, 0re: 14.00 / 16.00
X  0,622 
  Pvs (t )
P  (  Pvs )
Ricaviamo quindi X1 e X2 . Avrò che:
X  0,622 
0,8  0,4753
Kg v
g
 0,0245 
 24,5 v
1  0,8  0,4753
Kga
Kga
e, allo stesso modo, ottengo
gv
Kga
Possiamo così trovare il titolo 3
X 2  10,6
X3 
X 2  M 2 a  X 1  M 1a
g
 15,23 v
M 3a
Kg a
N.B: Si poteva ottenere ciò molto facilmente anche per via grafica: conoscendo
il punto 1 e il punto 2 è possibile determinare il punto 3 in quanto è la media pesata
in funzione dei titoli e delle temperature. Si rappresentano le due situazioni
termodinamiche all’ingresso dei due condotti e si ricava con i dati la situazione d’
uscita. Questa dovrà risultare su un segmento congiungente i due punti d’ ingresso.
Si scrive l’equazione per i sistemi aperti :
 h  q l  0
l’ entalpia specifica non cambia
= 0=0
Quindi, scritta in termini di entalpia specifica per Kg d’aria secca, scriviamo :
M 3a  J 3a  M 1a  J 1  M 2 a  J 2
Equazione che esprime semplicemente la legge di conservazione dell’energia
sotto forma di entalpia.
Si ricava da qui J 3
J 3a 
M 1a  J 1  M 2 a  J
M
3a
-10-
Data:13.12.2001, 0re: 14.00 / 16.00
Dobbiamo ricavare J1 e J2 . A tal fine basta ricordare la formula ricavata in
teoria per ottenerli.
J 1  t1  X 1  2500  1,9t1 
Kj
Kg a
 32  0,245  2500  1,9  32   94,7
Kj
Kg a
J 2  26  0,056  2500  1,9  26  56
Kj
Kg a
J 3  t 3  X 3  2500  1,9t 3 

Kj
Kg a
400  94,7  800  53
Kj
 66,9
1200
Kg a
J 3  2500  X 3 66,9  2500  0,01523

 28C
1  1,9  X 3
1  1,9  0,01523
 3  Ps 3
X 3  0,622 
P  Ps 3   3
t 
Ps 3  0,03778bar
3 
P X3
1  0,01523

 63%
Ps 3   X 3  0,622 0,03778  0,01523  0,622
-11-