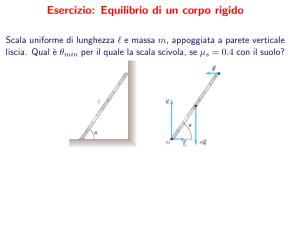
Problema 1:
Una scala di lunghezza L metri e massa M kg è appoggiata al muro con un’inclinazione α (ignota) rispetto al terreno.
Supponiamo per semplicità che sia trascurabile l’attrito muro-scala mentre il coefficiente di attrito statico del pavimento vale
µs . La scala è omogenea e quindi il suo centro di massa è in L/2. La scala è in equilibrio e l’angolo α è l’angolo limite oltre
il quale la scala scivola, cioè la forza di attrito statico esercitata dal pavimento è la massima possibile.
1. Calcolare il modulo della reazione vincolare, N, del pavimento.
2. Calcolare il modulo della forza Fa di attrito tra pavimento e scala.
3. Calcolare il modulo, Fm , della reazione vincolare del muro.
4. Calcolare l’inclinazione α della scala rispetto al terreno.
Problema 2:
Ad un oggetto, di massa m kg, inizialmente in quiete su un piano orizzontale senza attrito, viene applicata una forza parallela
al piano, costante, per un tempo di t secondi ed esso acquista una velocità di v m/s.
5. Calcolare il modulo della forza, F, applicata.
6. Successivamente il corpo sale lungo un piano inclinato privo di attrito. Calcolare la massima altezza, H, raggiunta.
Problema 3:
Una ruota di bicicletta è libera di ruotare attorno ad un asse passante per il suo centro O. Una forza costante di Fb N è
applicata ad un raggio della ruota in un punto P che dista d metri dal centro con una direzione che giace sul piano della
ruota ed è perpendicolare alla direzione del raggio con verso antiorario.
7. Qual è il modulo, M, del momento della forza agente sulla ruota?
8. Qual è la variazione, ∆L, del modulo del momento angolare della ruota dopo un tempo di τ secondi?
9. Se il momento di inerzia della ruota rispetto all’asse di rotazione è I ed inizialmente la ruota è ferma, qual è il modulo
della sua velocità angolare ω dopo lo stesso tempo τ ?
Problema 4:
Due blocchetti di massa rispettivamente m1 kg e m2 kg si muovono nello stesso verso lungo una traiettoria rettilinea con
velocità v1 m/s e v2 m/s. Quando il secondo corpo raggiunge il primo l’urto è totalmente anelastico.
10. Calcolare la quantità di energia cinetica, ∆E, dissipata nell’urto.
Soluzioni
Problema 1:
1. Le forze agenti sulla scala sono: la forza di reazione del muro e la forza di attrito tra scala e pavimento (dirette
orizzontalmente), la forza peso e la forza di reazione del pavimento (dirette verticalmente). Perchè la scala sia in
equilibrio la somma vettoriale delle forze agenti deve essere uguale a zero ed anche la somma vettoriale dei momenti
delle forze rispetto ad un qualunque polo deve annullarsi. Uguagliando a zero la somma delle forze lungo la direzione
verticale si trova che il modulo della reazione vincolare del pavimento è:
N = M g.
2. Il modulo della forza di attrito statico tra pavimento e scala, che corrisponde alla massima forza di attrito statico
possibile, è quindi dato da:
Fa = µs N = µs M g.
è:
Fm = Fa = µs M g.
4. Per trovare l’inclinazione della scala uguagliamo a zero i momenti delle forze calcolati prendendo come polo il punto di
appoggio della scala sul pavimento cosı̀ che il momento della forza di attrito e della reazione vincolare del pavimento
siano uguali a zero. I momenti delle forze sono tutti lungo una stessa direzione quindi possiamo tralasciare il segno di
vettore. Assegniamo, per convenzione, segno positivo al momento delle forze che farebbero ruotare la scala in verso
antiorario. Si ha quindi:
L
Fm Lsenα − M g cosα = 0.
2
Ma |Fm |=µs Mg da cui:
tgα =
1
1
→ α = arctg
.
2µs
2µs
Problema 2:
5. L’impulso della forza costante F esercitata per il tempo t è Ft. Per effetto della forza il corpo, inizialmente in quiete,
acquista la quantità di moto mv. Dalla relazione tra impulso e variazione della quantità di moto :
F t = mv → F =
mv
.
t
6. Le uniche forze che agiscono sul corpo sono la gravità (che è conservativa) e la reazione vincolare dei piani orizzontale ed
inclinato, che sono a lavoro nullo; si conserva quindi l’energia totale meccanica del corpo. Quando il corpo raggiunge la
sua massima ampiezza sul piano inclinato la sua velocità si annulla. Se imponiamo la conservazione dell’energia totale
meccanica del corpo tra la base del piano inclinato (dove abbiamo scelto di prendere lo zero dell’energia potenziale) ed
il punto di massima altezza, troviamo:
v2
1
mv 2 = mgH → H =
.
2
2g
Problema 3:
7. Per convenzione assumiamo come positivo il momento della forza che farebbe ruotare la ruota in senso antiorario. Con
questa scelta, quindi, il momento della forza Fb è positivo e vale:
M = Fb d.
8. Dato che la forza è costante nel tempo dalla relazione tra momento M della forza, calcolato nella domanda precedente,
e variazione del momento angolare (sono entrambi nella stessa direzione quindi possiamo omettere il segno di vettore)
si ha:
∆L = M τ = Fb dτ.
9. Il modulo del momento angolare di un corpo rigido in rotazione attorno ad un asse è L(t)= I ω(t) dove ω(t) è la velocità
angolare di rotazione attorno all’asse. Inizialmente la ruota è ferma, quindi ω=0 ed L=0. Dalla domanda precedente
sappiamo che, dopo un tempo τ il momento angolare è variato di ∆L, quindi L(τ )= ∆L e perciò:
L(τ ) = Iω(τ ) = ∆L → ω(τ ) =
Problema 4:
Fb dτ
Mτ
=
.
I
I
moto non ci sono forze esterne impulsive, perciò si conserva la quantità di moto totale del sistema. Dopo l’urto, quindi,
le due masse, unite, si muovono con velocità vf tale che:
m1 v1 + m2 v2 = (m1 + m2 )vf → vf =
m1 v1 + m2 v2
m1 + m2
L’energia cinetica iniziale, Eicin del sistema era:
i
Ecin
=
1
1
m1 v12 + m2 v22 ;
2
2
mentre quella finale è:
f
Ecin
=
1
(m1 + m2 )vf2 .
2
L’energia cinetica ∆E dissipata nell’urto è quindi:
f
i
∆E = Ecin
− Ecin
=
1
1
1
m1 v12 + m2 v22 − (m1 + m2 )vf2 .
2
2
2