Esercizio: Equilibrio di un corpo rigido
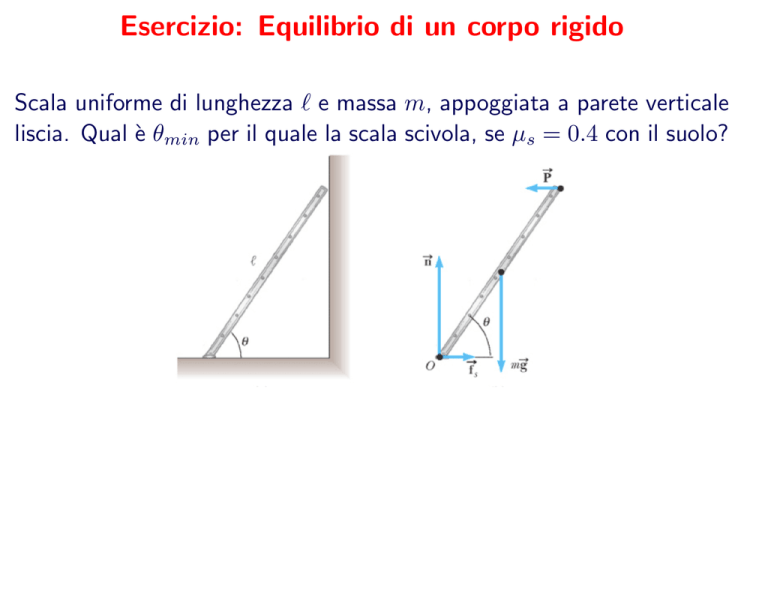
Scala uniforme di lunghezza ` e massa m, appoggiata a parete verticale
liscia. Qual è θmin per il quale la scala scivola, se µs = 0.4 con il suolo?
Esercizio: Equilibrio di un corpo rigido
Scala uniforme di lunghezza ` e massa m, appoggiata a parete verticale
liscia. Qual è θmin per il quale la scala scivola, se µs = 0.4 con il suolo?
Condizione di equilibrio sulle forze: n = mg, P = fa ≤ mgµs.
Condizione di equilibrio sui momenti (che conviene calcolare rispetto al punto O):
mg(`/2) cos θ = ` sin θP da cui P = (mg/2 tan θ) ≤ mgµs, condizione che può essere
rispettata solo se tan θ ≥ (1/2µs) = 1.25, ovvero θmin = 51◦.
Momento delle forze gravitazionali
Notare che il momento delle forze gravitazionali agenti su di un corpo è
uguale al momento della forza peso, concentrata nel centro di massa:
!
X
X
~τ =
~ri × (mi~g ) =
mi~ri × ~g
i
i
ma per la definizione di centro di massa:
!
X
X
~ cm = McmR
~ cm
mi~ri =
mi R
i
i
da cui
~ cm × (Mcm~g )
~τ = R
Esercizio: accelerazione angolare di una ruota
Una ruota di raggio R, massa M , momento
di inerzia I può ruotare su di un asse
orizzontale. Una corda è avvolta attorno
alla ruota e regge un oggetto di massa
m. Calcolare l’accelerazione angolare della
ruota, l’accelerazione lineare dell’oggetto, la
tensione della corda (si trascurino massa
della corda, attrito, resistenza dell’aria, etc.)
Soluzione: accelerazione angolare di una ruota
Momento torcente esercitato sulla ruota:
τ = T R, dove T è la forza esercitata dalla
corda sul bordo della ruota. Da Iα = τ si
TR
ottiene α =
.
I
Legge di Newton per l’oggetto sospeso:
mg − T = ma
→
mg − T
a=
m
Relazione che lega a e α: a = Rα, da cui
T R2 mg − T
a = Rα =
=
I
m
mg
T =
1 + (mR2/I)
Esercizio: Energia cinetica di un corpo che rotola
Corpo rigido di massa M , velocità del centro di massa v, momento
d’inerzia I per rotazioni attorno al centro di massa, velocità angolare ω.
Energia cinetica totale:
1
1 2
2
K = M v + Iω
2
2
Esempio: sfera (o cilindro) che rotola
giù per un piano inclinato. Avremo:
2
1 1
7
2
2
v = ωR , I = M R =⇒ K =
+
M v = M v2
5
2 5
10
Per la conservazione dell’energia meccanica, la velocità finale sarà
r
7
10
2
Ui = M g(h + R) = M v + M gR = Kf + Uf =⇒ v =
gh.
10
7
Dinamica di un corpo che rotola
Notare che l’energia potenziale gravitazionale di un corpo è la stessa che se tutta la
massa fosse concentrata nel centro di massa:
!
!
X
X
X
U=
mighi = g
mihi = g
mi hcm = M ghcm
i
i
i
Risolviamo ora il problema con forze e momenti.
• Lungo il piano: M a = M g sin θ − Fa, dove Fa è la forza di attrito.
• Rispetto al centro della sfera: Iα = τ = RFa, dove α = a/R.
I
2
2
5
Fa = 2 a = M a =⇒ (M + M )a = M g sin θ =⇒ a = g sin θ
R
5
5
7
ovvero un moto uniformemente accelerato, che può essere facilmente
risolto e dà lo stesso risultato del calcolo precedente. Notare che la
forza di attrito entra nelle equazioni del moto pur non facendo lavoro!
Esercizio (facoltativo): urto con rotazione
Disco di massa m = 2 kg che viaggia a vdi = 3 m/s colpisce asta
di massa M = 1 kg e lunghezza ` = 4 m ad un estremo, come in
figura. Disco e asta sono appoggiati ad una superficie ghiacciata con
attrito trascurabile. Conosciamo il momento d’inerzia I = 1.33 kg·m2
dell’asta attorno al suo centro di massa. Si assume che la collisione sia
perfettamente elastica e che il disco non sia deviato dalla sua traiettoria.
Determinare il moto (vdf , vs, ω) del sistema dopo l’urto.
Soluzione: urto con rotazione
1. Per la conservazione della quantità di moto: m~vdi = m~vdf + M~vs
(tutti i vettori lungo la stessa direzione)
2. Conservazione del momento angolare (calcolato rispetto alla posizione iniziale del
centro dell’asse) :
1
2 m`vdi
3. Conservazione dell’energia:
= 21 m`vdf + Iω (nella direzione ortogonale al piano)
1
2
mv
di
2
2
= 12 mvdf
+ 21 M vs2 + 12 Iω 2
Da (1): mvdi = mvdf + M vs; da (2): mvdi = mvdf + 2I
` ω, da cui: ω =
M`
2I vs
.
Da (1): vdf = vdi − M
m vs .
Sostituiamo ω nella (3):
1
2
2 mvdi
1
2
2 mvdi
=
1
2
2 mvdf
1
2
2 mvdi
+
1
2M
1+
M `2
4I
1 M2 2
2 m vs
vs2
1
2M
M `2
4I
Sostituiamo vdf :
+
=
− M vdivs +
1+
vs2, da cui
2
2
1
M
M`
M`
M
M
1
+
+
v
=
M
v
(se
v
=
6
0).
Infine
+
v
=
2v
/
1
+
s
di
s
s
di
2
m
4I
m
4I
Inserendo i dati: vs = 1.33 m/s, vf = 2.33 m/s, ω = 2.0 rad/s.












