LE PROIEZIONI ASSONOMETRICHE
La proiezione assonometrica fa parte delle proiezioni parallele, o
cilindriche.
Essa è caratterizzata quindi dall’avere il centro di proiezione all’infinito
(S∞
S∞), per cui è generata da raggi proiettanti paralleli tra loro, che
colpiscono l’oggetto nello spazio e vengono sezionati da un piano π , su cui
si forma l’immagine proiettata.
Affinché, però, si possa risalire alla posizione esatta dell’oggetto nello
spazio, esso viene collocato all’interno di un sistema di riferimento,
formato da una terna di piani π 1, π 2, π 3 ortogonali tra loro a due a due,
sui quali l’oggetto viene proiettato ortogonalmente; gli assi di intersezione
tra i piani suddetti risultano anch’essi ortogonali tra loro, convergono in
un punto O, origine del sistema di riferimento, e vengono denominati assi
di riferimento cartesiano x, y, z. Su ciascuno di essi è inoltre identificata
l’unità di misura.
Pertanto dal centro di proiezione S∞
∞ vengono proiettati, oltre all’oggetto
anche le sue proiezioni sui piani π 1, π 2, π 3, e la terna cartesiana x,y,z: sul
quadro, quindi, si avrà la vera proiezione assonometrica, sia dell’oggetto
che del sistema di riferimento, ma anche le tre proiezioni assonometriche
delle immagini dell’oggetto
In base alla direzione dei raggi proiettanti rispetto al quadro π, si ha:
Ass. ortogonale, se la direzione S∞
S∞ è ortogonale al quadro
Ass. obliqua, se la direzione S
S∞
∞ è obliqua al quadro
Nella proiezione del sistema di riferimento, in entrambi i casi di ass. obliqua
e ortogonale l’unità di misura (u
u) di ciascuno degli assi può avere
un’immagine assonometrica di dimensioni diverse da quella vera.
Il rapporto di riduzione u/u’ in cui u è il segmento dato e u’ la sua immagine,
dipende solo dalla direzione della retta r, che lo contiene, rispetto al piano.
Nell’assonometria obliqua si può avere:
u/u’< u oppure u/u’> u
Nell’assonometria ortogonale si ha:
u/u’= cos rr’ < u
rapporto di accorciamento
ASSONOMETRIA ORTOGONALE
IL TRIANGOLO DELLE TRACCE
Nell’assonometria ortogonale, si definisce triangolo delle tracce o fondamentale
quello formato dalle tracce dei tre piani di riferimento sul quadro, o dai segmenti
che congiungono le tracce dei tre assi di riferimento su π. La proiezione dell’origine
O, denominata O’, risulta essere l’ortocentro del triangolo delle tracce (Tx, Ty, Tz).
Per determinare u’x, u’y, u’z sulle immagini x’, y’, z’ occorre ribaltare il punto O sul
quadro, attorno ad almeno due dei lati del triangolo, per ottenere così la vera unità
di misura u.
Poiché il triangolo TzOTy è rettangolo in O, tale angolo dovrà mantenersi tale su l
piano p;dopo aver tracciato la semicirconferenza di diametro TzTy l’intersezione di
TxO’ con tale semicirconferenza individua O* ribaltamento di O su π. Unendo O* con
Tz e Ty si determinano z* e y* ribaltamento di z e y, sui quali a partire da O* si
riportano u*z e uy*.
Tra le immagini z’, O’, y’, e i ribaltamenti z*, O*, y* intercorre una affinità omologica
di ribaltamenti che ha per asse il lato TzTy, per centro U∞ la direzione ad esso
ortogonale e per elementi corrispondenti O’ e O* oppure z’ e z* etc.
Ricordando che punti corrispondenti sono allineati con il centro dell’omologia, è
possibile definire le unità asson. u’z e u’y. Si procede analogamente per trovare u’x.
Applicando le regole della trigonometria, esse risultano funzione degli angoli α, β, γ
che gli assi cartesiano formano con il quadro.
Il triangolo delle tracce e i rapporti di accorciamento possono essere determinati in
funzione degli angoli che gli assi X,Y,Z formano con x’, y’,z’.
ASSONOMETRIA ORTOGONALE
Determinazione delle unita’ assonometriche noti gli angoli
a ,b ,g.
Il triangolo delle tracce e i relativi
rapporti di accorciamento sulle
immagini degli assi, x’,y’z’, possono
essere determinati in relazione agli
angoli a b e g che gli assi x,y,z
formano con le loro immagini sul
piano di quadro.
Si dimostra che il triangolo delle
tracce è acutangolo, per cui noti
due angoli a e b il terzo angolo g
resta determinato.
Pertanto noti gli angoli è possibile
costruire il triangolo delle tracce
graficamente;viceversa noto il
triangolo delle tracce è possibile
determinare gli angoli a,b,g.
In figura, posizionati glia assi x’,y’,z’, e preso ad arbitrio Tz e O’, si è tracciato l’angolo g,
noto, e si è ottenuto O* sulla retta passante per O’ perpendicolare a z’, determinando così
u’z. Procedendo graficamente costruendo gli angoli noti, a e b, si determinano le tracce Tx e
Ty e si individuano le altre unità assonometriche u’x e u’y.
Assonometria Ortogonale
Determinazione delle unità assonometriche mediante il procedimento grafico che
consiste nel ribaltare i piani coordinati y’z’,x’y’, x’z’, sul piano di quadro
adoperando come cerniere di ribaltamento i lati del triangolo delle tracce.
Ass. trimetrica, se il triangolo delle
tracce è scaleno
α≠β≠γ u’x≠u’y≠u’z<1
Ass. dimetrica,se il
triangolo delle tracce è
isoscele
α ≠β
β ≠γγ u’x=u’y≠u’z<1
Ass. isometrica, se il triangolo delle tracce è equilatero α=β=γ u’x=u’y=u’z<1
Se le unità di misura
assonometriche hanno
valori tra loro uguali,
l’assonometria si dice
isometrica.
isometrica
Se su due assi le
unità hanno valori
uguali e sul terzo un
valore diverso, si
dice dimetrica
Se i tre valori sono tra loro distinti, l’assonometria si dice trimetrica
Rappresentazione di un
solido in assonometria
dimetrica assegnate le
proiezioni ortogonali
mediante ribaltamento
La pianta viene determinata
per omologia di ribaltamento:
u=TxTy (asse dell’omologia)
U∞⊥TxTy
La quota riportata sull’asse
viene determinata per
omologia:
u=TzTy (asse dell’omologia)
U∞⊥TzTy
ASSONOMETRIA OBLIQUA
Nel caso in cui la direzione di proiezione assonometrica S∞ è obliqua rispetto
al piano di quadro π, vale il cosiddetto teorema di Polke-Schwarz, secondo
cui, presa una qualsiasi terna di assi, comunque orientati, convergenti in un
punto, e tre valori di unità di misura, è sempre possibile risalire ad una
direzione assonometrica, a tre assi nello spazio mutuamente ortogonali ed a
tre rispettive unità di misura, di cui quelle date risultino essere le proiezioni
assonometriche.
In realtà si utilizzano tipi di assonometria obliqua in cui il quadro π risulti
parallelo o coincidente con uno dei piani cartesiani.
Questo tipo di assonometria è detto ass. cavaliera.
In tal modo, l’angolo formato dagli assi appartenenti al piano parallelo al
quadro rimane invariato, ovvero di 90°, per cui l’immagine assonometrica
conserva la forma e le dimensioni originarie.
In particolare, quando il quadro π è parallelo a π1, essa si chiama
ass. cavaliera militare.
L’immagine indeformata sarà quindi un prospetto o una pianta, a seconda che
si utilizzi la cavaliera o la cav. militare.
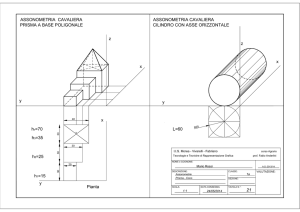
ASSON.
CAVALIERA
ASSONOMETRIA
CAVALIERA MILITARE
Per consuetudine si usano spesso terne di assi assonometrici che dividono
l’angolo in gio in 90°, 135°, 135° oppure in 90°, 120°, 150°, mentre per la
u’z i valori più utilizzati sono quelli di 1 o di 1/3 o 2/3 rispetto all’unità vera,
ma ciò viene fatto per comodità e non è vincolante.
RAPPRESENTAZIONE DEGLI ENTI GEOMETRICI
FONDAMENTALI
● I VARI TIPI DI ASSONOMERIA NON COMPORTANO CONCETTI
TEORICI DIVERSI PUR DETERMINANDO IMMAGINI DIFFERENTI.
● SARA’
QUINDI INDIFFERENTE PARLARE DI ASSONOMETRIA
ORTOGONALE O OBLIQUA.
● DI
UN ELEMENTO RIFERITO AD UNA TERNA TRIORTOGONALE DI
RIFERIMENTO SI DOVRANNO DETERMINARE LE PROIEZIONI
ORTOGONALI RISPETTO ALLA TERNA CARTESIANA STESSA
RAPPRESENTAZIONE DEL PUNTO
Assegnate le coordinate del
punto, tenendo presente che i
segmenti PP’ PP’’ PP’’’ sono
paralleli nello spazio alla terna
cartesiana di riferimento, è
semplice determinare le
proiezione del punto.
RAPPRESENTAZIONE DELLA RETTA
Per raffigurare una retta occorre
conoscere due sue proiezioni o due
sue tracce distinte, per potere
risalire a tutti gli elementi della
retta stessa.
RAPPRESENTAZIONE DEL PIANO
Per definire un piano basta dare due sole
tracce. E’ noto però che un piano è anche
individuato assegnando tre suoi punti distinti e
non allineati, una retta ed un punto non
appartenenti, due rette sue rette incidenti,
etc.
RAPPRESENTAZIONE DI UN SOLIDO IN ASSONOMETRIA
RAPPRESENTAZIONE DI UN CILINDRO IN ASSONOMETRIA
CAVALIERA MILITARE
Rappresentazione di
un cilindro sezionato
da un generico piano
α
Per costruire la figura di
sezione occorre
adoperare un piano
ausiliario che nel caso
specifico è stato scelto
in posizione radiale,
ovvero facendolo
ruotare n volte attorno
al centro della
circonferenza di base in
modo da individuare n
punti, che uniti daranno
la figura di sezione
cercata, ovvero,
l’ellisse.
Rappresentazione di
un cilindro sezionato
da un generico piano
α
Per costruire la figura di
sezione occorre
adoperare un piano
ausiliario che nel caso
specifico è stato scelto
in posizione parallela al
paino zy, ovvero
spostandolo n volte
parallelamente al piano
zy in modo da
individuare n punti, che
uniti daranno la figura
di sezione cercata,
ovvero, l’ellisse.
Rappresentazione di un
cilindro verticale intersecato
da un cilindro ad asse
orizzontale di raggio inferiore
Per costruire la figura di
sezione occorre
adoperare un piano
ausiliario che nel caso
specifico è stato scelto
in posizione parallela al
paino xz, ovvero
spostandolo n volte
parallelamente al piano
xz in modo da
individuare n punti, che
uniti daranno la curva di
intersezione cercata.