Esercitazioni del 07/04/2010
Il piano inclinato
Consideriamo un piano inclinato di un angolo ripetto all’ orizzontale e poniamo sopra
di esso un corpo di massa m. Quale sara’ il moto della massa m?
Soluzione
y
N
Px
Py
P
x
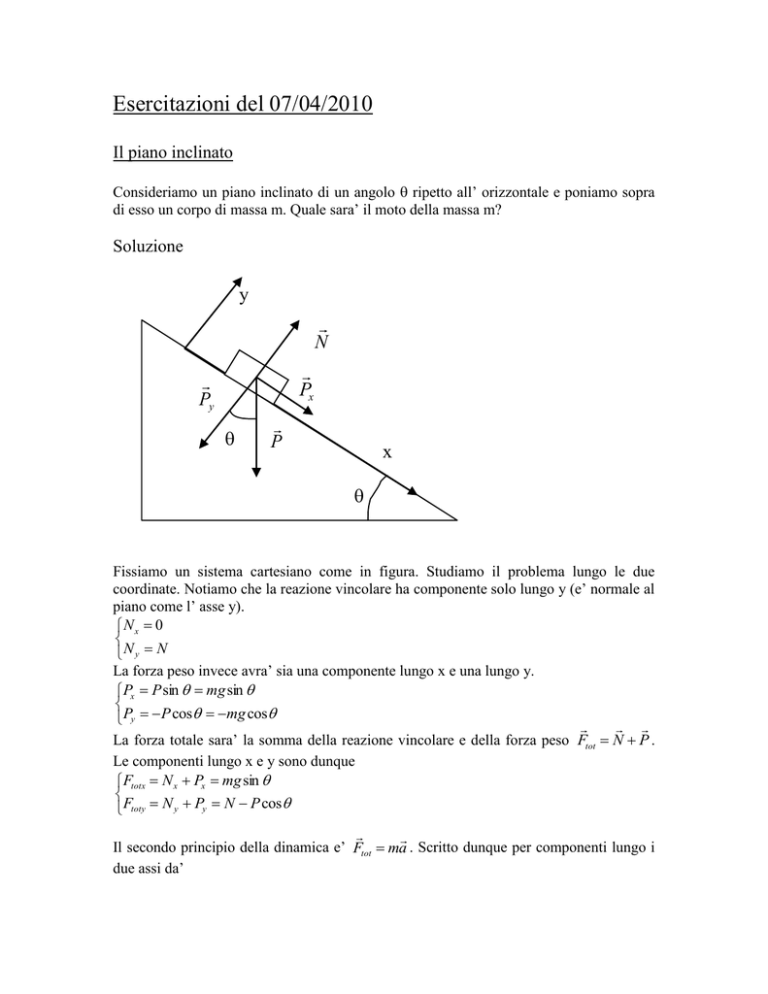
Fissiamo un sistema cartesiano come in figura. Studiamo il problema lungo le due
coordinate. Notiamo che la reazione vincolare ha componente solo lungo y (e’ normale al
piano come l’ asse y).
N x 0
N y N
La forza peso invece avra’ sia una componente lungo x e una lungo y.
Px P sin mg sin
Py P cos mg cos
La forza totale sara’ la somma della reazione vincolare e della forza peso Ftot N P .
Le componenti lungo x e y sono dunque
Ftotx N x Px mg sin
Ftoty N y Py N P cos
Il secondo principio della dinamica e’ Ftot ma . Scritto dunque per componenti lungo i
due assi da’
max Ftotx mg sin
may Ftoty N mg cos
Il vincolo costituito dal piano e’ impenetrabile e quindi l’ accelerazione lungo y e’ nulla
(ay=0). Percio’
0 N mg cos
N mg cos
Lungo x l’ accelerazione risulta dunque
ax g sin
La massa dunque e’ soggetta ad una accelerazione costante e compie percio’ un moto
uniformemente accelerato.
Il piano inclinato con attrito
Consideriamo il piano inclinato visto nel caso precedente questa con l’ aggiunta di attrito.
I coefficienti di attrito statico e dinamico tra il corpo e il piano sono s e d
rispettivamente. Quale sara’ il moto della massa m? Come dipende dall’ angolo ?
Soluzione
y
Fa
N
Px
Py
P
x
Supponiamo che sia sufficientemente piccolo che la massa m posta sul piano resti
ferma per azione della forza di attrito statico. Rispetto alle equazioni scritte nell esercizio
precedente avremo anche la presenza della forza di attrito statico che ha componenti
Fsx Fs
Fsy 0
poiche’ la forza di attrito e’ parallela all’ asse x. La forza totale e’ dunque
Ftot N P Fs . La seconda legge della dinamica scritta per componenti sara’ percio’
max Ftotx mg sin Fs
may Ftoty N mg cos
Nuovamente il vincolo da’ ay=0, cioe’ N mg cos come in assenza di attrito.
Abbiamo assunto che la massa rimanga ferma, quindi anche ax=0. Percio’
0 mg sin Fs
Fs mg sin
Si nota che la forza di attrito statico dipende dall’ angolo di inclinazione.
La forza di attrito statico e’ minore di un valore massimo, cioe’
Fs Fs ,max
con Fs ,max s N
Sostituendo nella disuguaglianza Fs e N ricavati precedentemente abbiamo
mg sin s mg cos
sin
tan s
cos
che da’
max arctan s
Si nota che la massa rimane ferma finche’ l’ angolo di inclinazione e’ minore di un certo
valore critico max .
Al di sopra di tale angolo la massa si muove e la forza di attrito sara’ di attrito dinamico.
Le equazioni scritte in precedenza sono tutte simili con la differenza che questa volta ax
sara’ diversa da zero.
max Ftotx mg sin Fd
may 0 Ftoty N mg cos
La forza di attrito dinamico vale
Fd d N
Quindi la seconda legge lungo x diventa
max mg sin d mg cos e cioe’
ax g sin d cos
Nel caso in cui il corpo avesse avuto una velocita’ iniziale negativa (cioe’ verso l’ alto) la
forza di attrito dinamico (che ha verso opposto alla velocita’) avrebbe avuto segno
positivo. In questo caso l’ accelerazione totale sarebbe stata
ax g sin d cos
Problema
Un corpo di massa m e’ posto con velocita’ nulla su un piano inclinato di altezza h=2m
ed inclinazione =300. Tra il piano e il corpo c’e’ attrito e i coefficienti di attrito statico e
dinamico sono s=0.25 e d=0.2. Si calcoli
1. l’ accelerazione del corpo
2. il tempo impiegato per arrivare in fondo al piano inclinato
3. la velocita’ con cui arriva in fondo.
Soluzione












