a/r

Lezione 6
Magnetostatica: forze magnetiche e campo magnetico
B (r )
(nomenclatura “storica”; in realtà si
dovrebbe chiamare, e spesso lo è,
campo magnetico)
è un “campo di forze” vettoriale nello
spazio, cioè una grandezza fisica con
modulo B ≡ B e direzione, funzione
della posizione nello spazio r = ( x, y, z )
(teorie di Faraday-Maxwell)
Campo di induzione
r r
magnetica
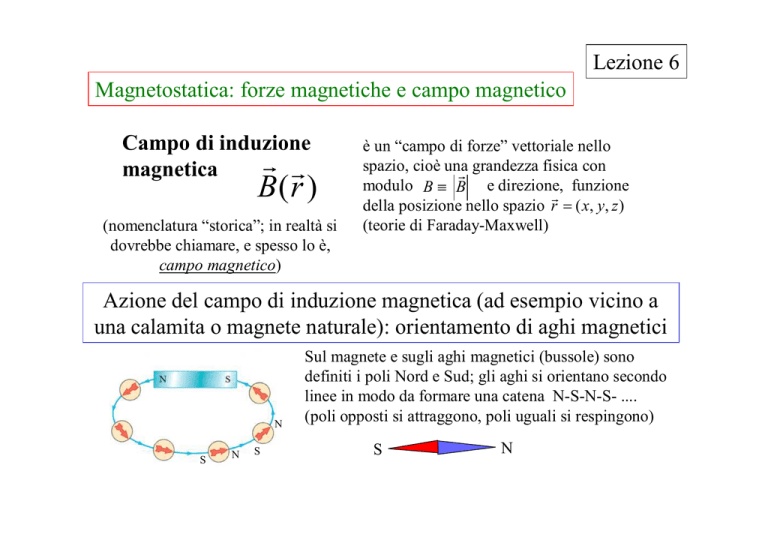
Azione del campo di induzione magnetica (ad esempio vicino a
una calamita o magnete naturale): orientamento di aghi magnetici
N
S
N
S
Sul magnete e sugli aghi magnetici (bussole) sono
definiti i poli Nord e Sud; gli aghi si orientano secondo
linee in modo da formare una catena N-S-N-S- ....
(poli opposti si attraggono, poli uguali si respingono)
S
N
Rappresentazione del campo magnetico per
mezzo di linee di forza: la direzione del
campo è tangente alle linee, che escono dal
polo N (Nord) ed entrano dal polo S (Sud)
r
B
Campo di induzione
magnetica della terra
Dipolo magnetico: oggetto simile al
dipolo elettrico: è formato da due poli
magnetici opposti a distanza d, la
struttura delle linee di forza è simile
Polo Nord
N
S
Terra
S
N
Polo Sud
Sole
Azione del campo di induzione magnetica: forze su fili percorsi
da una corrente elettrica
(seconda legge di Laplace)
r
B campo di induzione magnetica
r
∆l
N
tratto di filo, orientato nel verso
della corrente I
La forza è proporzionale alla corrente, alla
lunghezza del tratto di filo e al campo, ed è
diretta perpendicolarmente alle direzioni del
filo e del campo secondo la regola del cacciavite
(o della mano destra)
I
r
∆l
r
B
r r
r
F = I ∆l × B
vettore F = I ⋅ prodotto vettoriale tra i vettori ∆l e B
Più esattamente: forza infinitesima su un
tratto di filo di lunghezza infinitesima
r r
r
dF = I dl × B
S
r
F
Prodotto vettoriale
a è nella direzione di
avanzamento della vite
r
a
r r r
a = b ×cr
r
r
a perpend. a b e c
modulo a = b c sen θ
r
b
a = bc
a=0
θ
c × b = −b × c
il prodotto vettoriale
non è commutativo!
se b ⊥ c
se b || c
r
c
r
F
z
Forza del campo B
r r
r
F = I ∆l × B
modulo F = I B sen θ ∆l
r θ
∆l
r
B
y
x
terna di assi cartesiani
ortogonali (x,y,z)
[B] =
F
I ∆l
Si definisce il Tesla,
unità di misura di B
dimensioni di B =
1T =
F = I ∆l × B
La forza su fili definisce completamente B
[F ] = [I ∆ l B ]
Forza
Corrente ⋅ Lunghezza
1N
1 A ⋅1 m
Esempi: Elettromagnete B ≈ 2 T
Ferromagnete B ≈ 0.2 T
Campo magnetico terrestre ≈ 10-4 T
Si usa anche il Gauss: 1 Gauss = 10-4 T
Simbologia:
Campo entrante nel foglio
Campo uscente dal foglio
Forza totale su filo rettilineo in
campo magnetico uniforme e
perpendicolare al filo
dl
B costante, θ = π/2, sen θ = 1
F diretta verso sinistra
F=
∫ dF = ∫ I B sen θ
filo
filo
dl = I B ∫ dl = I B L
filo
L
r
F
I
direzione entrante nel piano
direzione uscente dal piano
Esempio di calcolo: forza totale su
un circuito semicircolare in campo
magnetico uniforme (vedi figura)
I
L
B diretto come x
r raggio del semicerchio
I corrente
d l tratto di filo infinitesimo
θ angolo tra la direzione di
dl e quella di B
y
O
θr
dl
r
F1
Forza sul tratto rettilineo del circuito:
direzione entrante nel piano
F1 = I L B
r
θ
dθ
r
F2
0
Forza sul tratto semicircolare: direzione uscente dal piano; dato che dl = r dθ e che
l’angolo va da 0 a π percorrendo il semicerchio (nel verso della corrente) si ha
F2 =
r
B
∫ I B senθ dl = ∫ I B r senθ dθ = I B r [− cos θ ]0 = 2 I B r = I B L
π
semicerchio
π
0
uguale e opposta alla precedente. Quindi la forza totale è nulla.
(questa conclusione è valida per spire di forma qualsiasi percorse da corrente!).
Sarà possibile però un moto di rotazione (coppia di forze e momento meccanico)
x
Momento meccanico su una spira
θ
Vista dall’alto
r
F1
r
F1
r
B
I
y
F2
x
r
B
Spira rettangolare di superficie S = a b,
con corrente I, immersa in campo
magnetico uniforme B diretto come x
Forze sui tratti diretti come x
(paralleli a B) : nulle
Forze sui tratti diretti come z
(perpendicolari a B) : F1 = F2 = I B b
x
r
F2
r
F2
F1 e F2 hanno direzioni opposte coppia di forze
moto rotatorio intorno al punto centrale O
momento meccanico rispetto a O:
a
a
a
M = F1 sen θ + F2 sen θ = 2 ⋅ IbB sen θ =
2
2
2
M = I ⋅ S ⋅ B ⋅ sen θ
F1
z
n
θ
r
B
Vista di fronte
Corrente entrante nel foglio
Corrente uscente dal foglio
Angolo tra B e la normale
alla superficie della spira
Momento meccanico = corrente · superficie · campo
θ =π
r
B
n
[M] = [I ⋅ S ⋅ B] = Am2 T = Am2
θ =π /2
r
B
o
n o
Momento meccanico zero
(posizione di equilibrio instabile)
energia massima U = + I S B
N
= Nm
Am
θ =0
n
Momento meccanico zero
(posizione di equilibrio stabile)
energia minima U = - I S B
Momento meccanico massimo
energia zero
M =ISB
U =0
Energia della spira nel campo magnetico: U = − I S B cosθ
(N.B la normale n alla spira
corrisponde alla regola del
cacciavite ruotando secondo la
rotazione della corrente)
(si ricava calcolando il lavoro meccanico per la rotazione della spira)
Motori elettrici: si ottiene lavoro meccanico sfruttando il movimento della spira nel
campo di induzione magnetica, variando nel tempo sinusoidalmente la corrente per
mantenere momento meccanico e rotazione (motori sincroni)
Il campo magnetico B viene generato da: magneti
⇒
N
S
Al limite le linee di forza di B si richiudono
su se stesse; non esistono cariche
magnetiche (differenza col campo elettrico)
Non ci sono sorgenti del campo B; si dice
che il campo B è solenoidale.
N
r
B
+
N
S
Non è possibile isolare
un polo magnetico (ad
esempio dividendo il
materiale in pezzi più
piccoli); i poli N e S
sono sempre accoppiati.
Geometria del campo B
∫ B ⋅ n dS
Legge di Gauss per B
ΦB =
= 0!
Sup. chiusa
S
e in forma puntuale
r
div B = 0
Lezione 7
Il campo magnetico B viene generato da: correnti
(prima osservazione sperimentale: Oersted 1819)
P
Il campo di induzione magnetica infinitesimo dB nel
punto P creato dal tratto di filo infinitesimo dl è dato
dalla legge di Biot-Savart (o prima legge di Laplace)
r
r
I
µ0 d l × r
dB =
I
4π
r3
dB =
µ0 I
senθ d l
2
4π r
 a) è perpendicolare a dl e a r secondo la
regola del prodotto vettoriale

r  b) è inversamente proporzionale a r2
dB  (legge dell’inverso del quadrato)
 c) è proporzionale alla corrente e alla
 lunghezza del filo
r
dl
dl
tratto infinitesimo di filo, orientato
nel verso della corrente I
r
r
vettore posizione del punto P da O
(ad angolo θ rispetto a dl )
in modulo:
O
in P: campo di induzione
magnetica B uscente dal foglio
(regola della mano destra)
Costante di proporzionalità µ0: dipende dalla scelta di definire B
dalla forza esercitata su fili percorsi da corrente (vedi)
Il campo di induzione magnetica B generato da
conduttori percorsi da correnti sarà quindi dato da
−1
4πε 0
C2
N
µ0
1
=
=
4π ε 0 µ0
N m 2 C 2 /s 2
1
Il rapporto tra le costanti nelle leggi che
definiscono i campi, costante elettrica /
costante magnetica è indipendente dalla
scelta dell'unità elettrica e ha le dimensioni
di una velocità al quadrato (… la luce…)
µ0 = 4π ⋅10 −7 Tm/A = 4π ⋅10 −7 N/A 2
Def.: permeabilità magnetica del vuoto:
m2
= 2 = c2
s
µ0 d l × r
B = ∫ dB = ∫
I
3
4
π
r
fili
fili
r ∂Bx ∂B y ∂Bz
Si dimostra che per i campi
div B =
=0
+
+
magnetici generati da correnti vale
∂z
∂y
∂x
seconda equazione di Maxwell:
la divergenza di B è sempre zero
(a meno che non venga scoperto un monopolo magnetico ……)
campo di induzione magnetica B generato da conduttore rettilineo
Calcoliamo il campo nel punto P, a distanza R
dal punto di intersezione del filo col piano
Osserviamo che: dl = dz
z
O
+∞
−∞
dl
θ
=
µ0 I
2π R
µ0 I
Quindi B è inversamente
B=
proporzionale alla distanza dal filo
2π R
R
r
r
R
r2 = z2 + R2
senθ = ;
r
µ I
B(in P) = ∫ dB = ∫ 0 2 senθ d l =
4π r
filo
filo
µ0 +∞
µ0
R
z
=
=
I∫
dz
I
4π −∞(z 2 + R2 )3/ 2
4π R z 2 + R 2
I
Filo conduttore infinito diretto come z e percorso da
corrente I; B è perpendicolare al filo e quindi giace su un
qualunque piano perpend. al filo. Data la simmetria
cilindrica, le linee di forza del campo B sono circolari.
B
P
vista dall’alto: osserviamo che la
direzione delle linee di forza
circolari e la direzione della
corrente sono legate dalla regola
del cacciavite (o mano destra)
r
B
campo di induzione magnetica B sull’asse di una spira circolare
z
dB 1 cos θ
θ
d B2
d B1
Spira circolare di raggio a, percorsa da corrente I e
giacente sul piano x-y; sul punto indicato dell’asse, il tratto
di spira dl1 contribuisce al campo di induzione magnetica
per la quantità dB1 ; dato che dl1 è perpendicolare al raggio
vettore r1 si ha:
d l1 × r1
µ
µ I
µ0 I
dl1
dB 1 = 0 I
= 0 2 dl1 =
3
4π
4π (z 2 + a 2 )
4π r1
r1
Per la simmetria circolare, il tratto di spira dl2, opposto a dl1,
contribuisce con il campo dB2 che ha la stessa componente su
z, ma componente opposta sul piano x-y. Quindi la parte di
campo di induzione magnetica che non si annulla è dB1 cosθ
(con cosθ = a/r1). Il campo totale B è diretto come z e vale:
µ0 I
B = dB1 cos θ =
cos θ dl1 =
2
2
π
z
a
(
)
4
+
spira
spira
=
4π (z + a
2
2
)
a
z +a
2
B( z ) =
µ0 I a
µ0 I
dl1 =
2
(
spira
4π (z + a
2
µ0 I a 2
2 z +a
2
)
2 3/ 2
)
2 3/ 2
r1
r2
d l2
θ
x
a
y
I
d l1
r
B
2π a
I
la direzione delle linee di forza e la
direzione della corrente sono legate dalla
regola del cacciavite (o mano destra)
Forza magnetica tra conduttori paralleli
Due conduttori paralleli di lunghezza L e a
distanza d con correnti I1 e I2 di verso concorde
µ I
Il conduttore 1 genera un campo B1 (r ) = 0 1
2π r
(diretto come linee di forza circolari)
r
B1
d
Sul conduttore 2 agisce la forza F1 = I 2 ∆l2 × B1 ( d )
I1
r
F1
()
r
I2 F
2
µ 0 I1 I 2
L e direzione verso il conduttore 1
2π d
Per simmetria (come è evidente
Due conduttori paralleli con correnti
dalla
formula)
anche
sul
nello stesso verso si attraggono con F = µ 0 I1 I 2
⇒
conduttore 1 agisce la stessa
L 2π d
una forza per unità di lunghezza :
forza, diretta verso il conduttore 2
(legge di azione e reazione)
di modulo F1 = I 2 L B1 ( d ) =
Se le correnti scorrono in versi
opposti (discordi) è evidente che
le forze sono in direzioni opposte
⇒
Due conduttori paralleli con correnti
F µ 0 I1 I 2
in versi opposti si respingono con
=
L 2π d
una forza per unità di lunghezza :
La definizione precisa dell’Ampere (unità di misura della corrente elettrica del
Sistema Internazionale) avviene attraverso la misura di forze tra fili conduttori
Campi E e B: alcune somiglianze e differenze
⇒
∫ E ⋅ n dS =
Sup. chiusa
Qcont
ε0
del campo: ⇒
⇐ geometria
Legge di Gauss
Campo conservativo, esiste
la funzione Potenziale e
r r
∫ E ⋅ ds = 0
∫ B ⋅ n dS = 0
Sup. chiusa
Esiste funzione Potenziale ?
(No!, si vedrà più avanti)
Lavoro delle forze
del campo
⇐
ΦB =
Non permette di calcolare B !
Permette di calcolare E per varie
configurazioni di cariche
percorso
chiuso
div B = 0
ΦE =
ρ
ε0
dB =
linee di forza
div E =
µ0 d l × r
I
4π
r3
r
r
generazione del campo
Q
r2
⇐
Da correnti elettriche
(cariche in movimento)
Legge di Biot-Savart
E (r ) = k
Da cariche elettriche:
(dalla legge di Coulomb)
Campo magnetostatico
Campo elettrostatico
r
B
r
E
circuitazione
⇒
r r
∫ B ⋅ d s = ??
percorso
chiuso
Teorema di Ampere
Dalla legge di Biot-Savart (o prima legge di
Laplace) si ricava il Teorema di Ampere:
circuitazione di B ⇔ corrente concatenata
I3
I3
I4
C
I2
percorso
chiuso
corrente concatenata, cioè corrente totale stazionaria che passa
all’interno del percorso chiuso di integrazione, presa col segno
positivo se la direzione corrisponde alla regola della mano
destra o del cacciavite (segno negativo nel caso opposto)
(più esattamente IC è la corrente che passa attraverso una
qualunque superficie che ha per bordo il percorso chiuso C)
IC
I1
r r
∫ B ⋅ ds = µ 0 I C
Esempio: nel sistema di fili percorsi
da corrente come in figura, la corrente
concatenata al circuito C vale:
r
I C = I1 − I 2
il Teorema di Ampere svolge per B le
stesse funzioni della legge di Gauss per E
Campo magnetico creato da un conduttore rettilineo di
raggio R, percorso da corrente I0 distribuita uniformemente
B
ds
Data la simmetria cilindrica le linee di forza di B sono
circolari, e dirette come le frecce per la regola della mano
destra (o cacciavite)

B ⋅ ds = ∫ B(r ) ⋅ d s = B(r ) ⋅ ∫ d s = B(r ) ⋅ 2π r = µ I
∫

µ I
B
r
(
)
=
I
=
I

2π r
Per r > R, all’esterno del conduttore, calcoliamo il campo B
scegliendo un percorso circolare (cerchio 1):
r
0



cerchio 1
corrente concatenata:
cerchio 1
0
cerchio 1
C
C
Per r < R, all’interno del conduttore, calcoliamo il campo B
scegliendo ancora un percorso circolare (cerchio 2):
∫ B ⋅ ds = B(r ) ⋅ 2π r = µ
0
(risultato già noto)
B (r )
1
r
r
IC
cerchio 2
π r2
IC = I0
π R2
la corrente concatenata è la frazione della corrente totale
che passa all’interno del cerchio 2
B( r ) =
µ0 I 0
r
2
2π R
o
R
Grafico di B(r)
r
I
il solenoide
Il solenoide è costituito da un filo conduttore avvolto a
elica e percorso dalla corrente I ; nel caso ideale di
solenoide infinito il campo B rimane confinato
all’interno, ed è quasi uniforme (per simmetria).
L
circuito
1
2
3
Corrente concatenata:
4
B ⋅ d s = ∫ B ⋅ ds + 02,3,4 = B ⋅ L
1
IC = n ⋅ L ⋅ I
(n: numero delle spire per unità di lunghezza)
B ⋅ L = µ0 I C
⇒ B = µ0 n I
(formula valida al centro di solenoidi molto lunghi)
Linee di forza di B per un solenoide realistico
r
B≠0
B=0
∫ B⋅ d s = ∫ + ∫ + ∫ + ∫
Calcolo del campo magnetico con il Teorema di Ampere:
si considera il circuito rettangolare in figura
Lastra conduttrice di piccolo spessore s percorsa da densità di corrente J
3
Corrente concatenata:
J
4
IC = J ⋅ s L
1
B = µ0 s J
2
Bobina toroidale con N spire percorse dalla corrente I
Se le spire sono molto fitte, il campo B è confinato all’interno
della bobina e (per simmetria) tangente al cerchio di raggio r,
centrale alle spire. Calcoliamo il campo su questo cerchio:
∫ B(r) ⋅ ds = B(r) ⋅ 2π r
Corrente concatenata: I C = N ⋅ I
cerchio
B=
µ0 N I
2π r
(N.B. dipende da r, cioè non è costante all’interno della bobina)
4
y
J
1
x
J=
2
z
s
1
3
L
2
B ⋅ ds = 2BL
circuito
B
∫ B ⋅ ds = ∫ + ∫ + ∫ + ∫
Per una lastra di grande superficie, B è quasi
uniforme; se la corrente scorre verso x, per la
regola della mano destra le linee di forza di B
sono orientate verso +y in basso e –y in alto.
Sul circuito rettangolare di lato L:
corrente
superficie
r
B