Capitolo5: Azionamenti con motori asincroni
La coppia prodotta dal motore vale allora:
C
(5.61)
P (1 S)
P
Pm
Rr
t
t 3
I 2r
0 (1 S) 0
S 0
Trascurando I0 nel modello di Fig.5.16 (11), la corrente di rotore vale, in valore efficace:
I 2r
(5.62)
Vs2
2
R
2
R s r X ks
S
,
dunque l’espressione della coppia diviene:
3Vs2
Rr /S
C
2
0
Rr
2
R
s
X ks
S
(5.63)
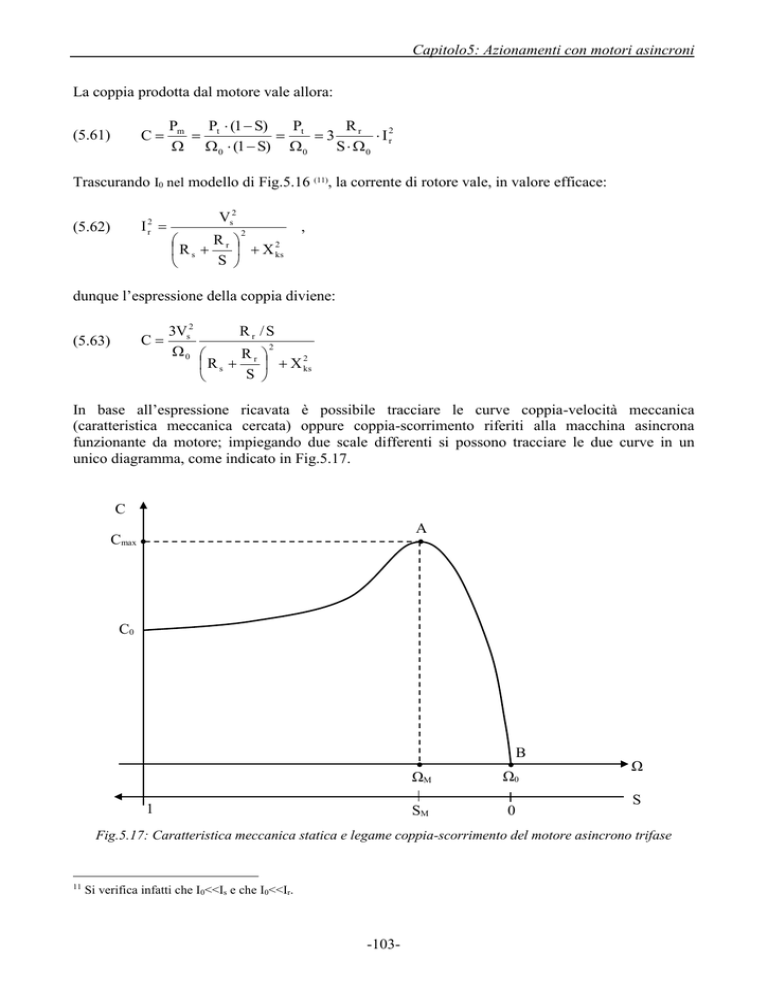
In base all’espressione ricavata è possibile tracciare le curve coppia-velocità meccanica
(caratteristica meccanica cercata) oppure coppia-scorrimento riferiti alla macchina asincrona
funzionante da motore; impiegando due scale differenti si possono tracciare le due curve in un
unico diagramma, come indicato in Fig.5.17.
C
A
Cmax
C0
B
1
ΩM
Ω0
SM
0
Ω
S
Fig.5.17: Caratteristica meccanica statica e legame coppia-scorrimento del motore asincrono trifase
11
Si verifica infatti che I0<<Is e che I0<<Ir.
-103-
Francesco Della Torre - Azionamenti elettrici
All’avviamento si ha Ω=0, S=1 e la coppia vale:
(5.64)
C0
3Vs2
Rr
0 R s R r 2 X 2ks
Mentre invece lo scorrimento corrispondente al punto di coppia massima vale:
(5.65)
SM
Rr
R X 2ks
2
s
,
da cui si ricava che la coppia massima è:
(5.66)
C max
3Vs2
0
Rr
Rs
2 R s2 X 2ks 1
2
R s X 2ks
Rr
3Vs2
0 2 R s2 K 2KS 2 R s
Il tratto stabile della caratteristica va dal punto A=(C max, ΩM) al punto B=(0, Ω0). Si noti come il
motore non possa mai funzionare in condizioni di sincronismo (punto B) in quanto, per esso, si ha
coppia prodotta nulla. In effetti la possibilità di esistenza di un punto di lavoro di regime è legata
alla presenza di uno scorrimento non nullo fra il campo rotante di statore ed il rotore; l’unico caso in
cui ci si potrebbe trovare al sincronismo è quello per cui si ha funzionamento a vuoto, ma nella
realtà anche in tale situazione la velocità è inferiore ad Ω0 a causa delle perdite addizionali e delle
perdite meccaniche per attrito e ventilazione, fin qui trascurate ma comunque presenti.
Il campo di operatività della macchina si traccia considerando il servizio continuativo e tenendo
conto dei seguenti vincoli:
Le caratteristiche di isolamento e raffreddamento impongono la tensione nominale di statore
Vs,n;
Il tipo di materiale ferromagnetico impiegato limita il flusso e ne impone il valore nominale Ψ n,
sia per lo statore che per il rotore;
Le parti meccaniche impongono un limite sulla massima velocità di rotore Ωmax;
Gli avvolgimenti impongono un limite alle correnti circolanti; nell’ottica dell’impiego del
motore asincrono in un azionamento, tale limite è imposto in concomitanza con la corrente
massima che può circolare nel convertitore statico a monte del motore.
Come per il motore a corrente continua, anche in questo caso il campo di operatività sarà diviso in
due distinte zone:
0<Ω<Ωb: inizialmente si cerca di sfruttare al meglio il ferro della macchina, dunque si lavora a
flusso costante e pari al suo valore nominale; per ottenere un aumento della velocità è necessario
allora aumentare la tensione di statore, fino a raggiungerne il valore nominale, in cui la velocità
di rotore ha raggiunto il suo valore base Ωb;
-104-
Capitolo5: Azionamenti con motori asincroni
Ωb<Ωb<Ωmax: superata la velocità base, l’unico modo per aumentare ancora la velocità del rotore
è quella di diminuire il flusso di macchina: si è dunque in zona di deflussaggio.Trascurando le
cadute resistive di statore, risulta, dalla prima delle (5.58):
(5.67)
vs s ,
JXksIs
dunque in zona di deflussaggio la tensione viene
mantenuta costante ed il flusso diminuirà come 1/Ω.
Vs
RrIs
Il campo di operatività è da completare valutando gli
andamenti della coppia e della coppia massima; dalla (5.66) è
facile vedere che:
(5.68)
C max
Vs2
2
f
, f
0
2 n 2 n (1 S) 2
Inoltre, tenendo conto che il diagramma vettoriale di regime (12)
è quello rappresentato in Fig.5.18, si ha:
(5.69)
C
Es
Er
1
E s I s cos s I s cos
0
Is
γ
Ir
I0
Fig.5.18: Diagramma vettoriale
relativo ad una fase della macchina
asincrona in regime sinusoidale
Superata la velocità per cui la coppia è massima, anche la coppia stessa presenta variazioni
proporzionali ad 1/Ω2, in quanto deve mantenersi pari al valor massimo.
In base a tutte le considerazioni fatte, il campo di operatività è quello rappresentato in Fig.5.19.
Cmax
≡1/Ω2
C
Ψ
≡1/Ω2
≡1/Ω
≡1/Ω
V
≡Ω
Ωb
Fig.5.19: Campo di operatività del motore asincrono trifase
12
Le grandezze E indicano le forze elettromotrici di statore e di rotore a regime.
-105-
Ωmax
Ω
Francesco Della Torre - Azionamenti elettrici
5.5 Descrizione dei blocchi impiegati negli schemi di controllo
Nei vari schemi di controllo per gli azionamenti con motore asincrono che verranno ora presentati
compariranno alcuni blocchi che, per varie ragioni, saranno estremamente semplificati rispetto agli
analoghi visti per gli azionamenti con motore in corrente continua; dunque è necessario, prima di
esporre le varie tecniche, mostrare tale blocchi e fare alcune considerazioni.
5.5.1 Blocco “Motore asincrono trifase”
Come visto ai paragrafi precedenti, il
motore asincrono è un sistema
ia(t)
elettromagnetico fortemente non lineare, va(t)
dunque
non
potrebbe
essere vb(t)
ASIN
ib(t)
rappresentato nel dominio di Laplace; in
3~
realtà ciò viene reso possibile vc(t)
ic(t)
linearizzandone il sistema descrittivo
attorno ad un punto di funzionamento e
ricavandone le relative funzioni di
trasferimento. Poiché questo non rientra
negli scopi delle presenti Note, le quali
Ω(t)
( t )
vogliono soltanto essere uno strumento di
analisi dei vari tipi di azionamento, si
rimanda
a
lavori
più
specifici
Fig.5.20: Rappresentazione impiegata per il motore
sull’argomento (13) per una trattazione
asincrono trifase
completa. Per tale motivo il blocco
relativo al motore asincrono trifase verrà qui rappresentato semplicemente come in Fig.5.20,
intendendo che esso rappresenta la macchina descritta dalle equazioni viste in precedenza
accoppiata con il carico meccanico in questione; tale blocco, che verrà denominato come
“ASIN3~”, presenta come ingressi le tensioni statoriche va(t), vb(t), vc(t) o le correnti statoriche ia(t),
ib(t), ic(t) e come possibili uscite la velocità meccanica, la posizione angolare, la terna di correnti
statoriche ia(t), ib(t), ic(t) o la terna di tensioni statoriche va(t), vb(t), vc(t); è opportuno osservare che,
avendo ipotizzato il sistema come simmetrico ed equilibrato, in realtà le correnti da misurare
potrebbero essere soltanto due in quanto la terza è ricavabile per differenza.
5.5.2 Blocco inverter
Gli inverter impiegati per il
controllo verranno rappresentati
y1
y
1,c
come dispositivi in grado, in base
ingressi y2,c
y
2
ai segnali di controllo applicati,
INV
di controllo
uscite
di fare in modo che le grandezze
y
3,c
y3
in uscita inseguano fedelmente le (modulanti )
variabili di riferimento; questo
permette di pensare al relativo
Fig.5.21: Rappresentazione impiegata per gli inverter
blocco come un sistema avente
funzione
di
trasferimento
costituita da un guadagno statico e da un polo reale che rappresenta il ritardo con il quale, nella
realtà, l’inverter fornisce le variabili in uscita. Il blocco con il quale verranno rappresentati gli
Vedasi, ad esempio, G.Superti Furga, “Modellistica dei sistemi elettromeccanici”, dispense del corso tenutosi al
Politecnico di Milano-Dipartimento di Elettrotecnica, disponibili sul sito http://www.etec.polimi.it .
13
-106-
Capitolo5: Azionamenti con motori asincroni
inverter è dunque quello di Fig.5.21; si noti che, a seconda del tipo di inverter, gli ingressi e le
uscite potranno essere costituite da tensioni (VSI), da correnti (CSI) oppure da correnti gli ingressi e
da tensioni le uscite (Inverter CRPWM, ossia “Current Ratio Pulse Width Modulation”); è
necessario però non dimenticare che anche i segnali di corrente sono in realtà dei segnali in
tensione.
Anche per gli inverter valgono le considerazioni già fatte per il motore circa una loro possibile
rappresentazione nel dominio di Laplace mediante linearizzazione attorno ad un punto di
funzionamento; si osservi che la semplificazione qui adottata vale perfettamente con inverter a
tecnica di controllo PWM ad elevata frequenza di commutazione (tipicamente > 3 kHz), mentre in
altre situazioni potrebbe risultare troppo grossolana. Infine è necessario osservare che, nel caso di
inverter comandati con tecnica di modulazione “Trifase Space Vector”, il problema sarebbe ben più
complesso in quanto tale tecnica è realizzata, come già discusso al capitolo 2, mediante dispositivi
numerico-digitali che presupporrebbero l’impiego di tecniche di calcolo, progettazione e
rappresentazione dedicate (14).
5.5.3 Blocchi “Trasformata di Park” e “Trasformata inversa di Park”
Negli schemi di azionamento che verranno descritti vi sarà la necessità di ottenere le grandezze in
gioco nel dominio di Park a partire dalle grandezze reali; i blocchi con i quali vengono
rappresentate le Trasformate su assi fissi e su assi rotanti e le relative antitrasformate sono
rappresentati in Fig.5.22 e Fig.5.23; essi “lavorano” secondo la Teoria (e le relative equazioni)
esposta al paragrafo 5.3.2. Si osservi come in uscita non venga prelevata la grandezza omopolare in
quanto essa non interviene, secondo quanto visto in precedenza, nel modello impiegato.
( t )
ya(t)
yb(t)
[T0]
yα (t)
yb(t)
yβ (t)
yc(t)
ya(t)
[T2]
yq (t)
yc(t)
(Trasformata diretta)
yd (t)
(Trasformata diretta)
( t )
yα (t)
ya(t)
[T0]t
yβ (t)
yd (t)
yb(t)
yc(t)
(Trasformata inversa)
ya(t)
[T2]t
yq (t)
yb(t)
yc(t)
(Trasformata inversa)
Fig.5.22: Blocchi impiegati per rappresentare la
Trasformata di Park su assi fissi e la relativa
Fig.5.23: Blocchi impiegati per rappresentare la
Trasformata di Park su assi rotanti e la relativa
14
Il sistema che ne risulta è di tipo ibrido, ossia costituito da segnali sia analogici che digitali; la definizione di una
funzione di trasferimento equivalente nel dominio di Laplace a partire da ciò è complessa (cfr. anche paragrafo 3.8 per
farsi un’idea, seppur vaga, delle problematiche in questione…).
-107-
Francesco Della Torre - Azionamenti elettrici
antitrasformata
antitrasformata
5.6 Controllo scalare
E’ la tecnica di controllo impiegata in tutti quei casi in cui si hanno specifiche dinamiche di medio
livello; si basa sull’andamento del campo di operatività visto in precedenza ed in particolare: fino
alla velocità base viene mantenuto costante il rapporto fra il modulo (ampiezza) della tensione
statorica e la frequenza (legata alla velocità), mantenendo in tal modo il flusso concatenato costante
e pari al valore nominale; successivamente si opera un deflussaggio della macchina, mantenendo
costante la tensione statorica al suo valore nominale (col che il flusso decresce, come visto, come
1/Ω). Lo schema di controllo è abbastanza elementare; esso è rappresentato in Fig.5.24.
|V|
|Vs|
va,c
Ωrif
n
ω
ωrif
K | Vs | e js
V/Hz
1/s
va
vb,c
INV
vc,c
vb
vc
ASIN
3~
s
Tensioni di fase
Fig.5.24: Controllo scalare del motore asincrono trifase
Il blocco “tensioni di fase” genera, a partire dal modulo della tensione statorica e dall’angolo fra gli
assi d,q e gli assi fissi, le tensioni statoriche di riferimento nel seguente modo:
(5.70)
v ( t ) K | V | cos ( t )
s
s
a
2
v b ( t ) K | Vs | cos s ( t ) , K
3
2
v c ( t ) K | Vs | cos s ( t )
3
2
3
Tali segnali vengono poi impiegati come modulanti per il
controllo PWM dell’inverter che alimenta il motore
asincrono.
Il blocco “V/Hz” (leggasi “Volt su Hertz”) fornisce in
uscita, in base al campo di operatività, il modulo della
tensione statorica a seconda della pulsazione del campo
rotante di statore; esso, in realtà, presenta un valore di
tensione non nullo, detto Vboot, in corrispondenza di valori
nulli di tale pulsazione (cfr. Fig.5.25); ciò è dovuto al fatto
che, anche se nella (5.67) è stata trascurata la resistenza Rs
di statore, in condizioni di avviamento tale resistenza
provoca una caduta di tensione non trascurabile e pari,
appunto, a Vboot.
Si noti come tale schema sia realizzato ad anello
aperto, senza alcun controllo in retroazione dell’effettiva
-108-
|Vs|
Vboot
ω=nΩ= s
Fig.5.25: Caratteristica reale del blocco
V/Hz
Capitolo5: Azionamenti con motori asincroni
velocità del motore; ciò implica senz’altro minori costi di esecuzione ma anche, come anticipato, un
suo impiego in situazioni con specifiche dinamiche poco spinte.
5.7 Controllo “Volt su Hertz”
Trattasi in sostanza di un controllo scalare che migliora lo schema di base di cui al paragrafo
precedente. Esso è basato sull’osservazione che si è praticamente obbligati a lavorare sul tratto di
stabilità della caratteristica meccanica (cfr. Fig.5.17, tratto AB); in tale tratto, come verrà ora
mostrato, la coppia è direttamente proporzionale, sotto certe condizioni, alla pulsazione ω e dunque
alla velocità Ω. Per dimostrare tale proprietà, si immagini che l’asse d di Park sia sempre allineato
con il favore spaziale del flusso rotorico, ossia che risulti sempre:
(5.71)
r rd r
rq 0
Si riprenda ora il modello dinamico a quattro parametri visto in precedenza (cfr. Fig.5.11);
l’equazione di rotore è rappresentata dalla seconda delle (5.55), ossia:
(5.72)
0 R r i r p r j
r
r
Ricordando ora la quarta delle (5.54):
(5.73)
r M (is i r ) i r
r
is ,
M
e che r s , la (5.72) diviene:
(5.74)
0
Rr
)
r R r is p r j(
s
r
M
Scomponendo tale equazione sugli assi d,q di Park si ha, tenendo conto di (5.71):
(5.75)
Rr
r R r i sd p r
d : 0
M
)
q : 0 R r i sq j(
s
r
,
dalla seconda delle quali si ricava:
(5.76)
) r
i sq (
s
Rr
L’espressione della coppia nel dominio di Park è stata ricavata in precedenza (vedasi la (5.36) e nel
presente caso si particolarizza come:
(5.77)
C n ( rd i sq rq i sd ) n ( r i sq ) n
2r
) K (
) ,
( s
s
Rr
-109-
Francesco Della Torre - Azionamenti elettrici
espressione che a regime diviene:
(5.78)
C KS ,
come volevasi dimostrare; in tale espressione il prodotto ωS è detto “coppia di scorrimento” mentre
la costante K è detta “costante di coppia”.
Sfruttando allora quanto appena ricavato è possibile costruire lo schema del controllo
denominato “Volt su Hertz”, derivandolo da quello visto al paragrafo precedente (cfr. Fig.5.24) e
chiudendo quest’ultimo in retroazione come mostrato in Fig.5.26, nella quale viene anche indicato il
trasduttore di velocità necessario.
|V|
|Vs|
Ωrif
Regolato
re
di
velocità
Crif
1/K
ω
ωrif
s
K | Vs | e js
V/Hz
1/s
va,c
va
vb,c
INV vb
vc,c
vc
ASIN
3~
s
Tensioni
di fase
n
Ωmis
Ω
H1
Fig.5.26: Controllo “Volt su Hertz” del motore asincrono; H1 indica il trasduttore di velocità
5.8 Controllo vettoriale (o “ad orientamento di campo”) indiretto
I sistemi di controllo diretto forniscono transitori meccanici molto soddisfacenti, mentre invece il
transitorio elettromagnetico presenta elevate sovraelongazioni di corrente, specie in fase di
avviamento. Per migliorare quest’ultimo è possibile impiegare la famiglia dei controlli vettoriali
(detti anche “ad orientamento di campo”), basata sull’idea di considerare una macchina equivalente
a collettore della macchina asincrona (operazione efficacemente facilitata dalla visione vettoriale
insita nella Trasformata di Park); ragionando su quest’ ultima sarà poi possibile, idealmente,
adottare le tecniche utilizzate per il controllo della macchina a corrente continua. Per far ciò si
ipotizzerà uno dei due assi mobili d,q solidale con il flusso r , ad esempio l’asse d; un osservatore
solidale con tale asse vedrà allora una corrente, la isd, solidale col flusso, dunque assimilabile a
quella circolante nel circuito di eccitazione della macchina a corrente continua, responsabile del
flussaggio della macchina equivalente; vedrà poi una corrente, la isq, in quadratura rispetto al flusso,
dunque assimilabile a quella circolante nell’avvolgimento di armatura, responsabile della
generazione della coppia.
A seconda del flusso che si decide di allineare con l’asse d si hanno vari tipi di controllo vettoriale:
FAM (Flux Acceleration Method)
SFOC (Stator Field Oriented Control)
MFOC (Magnetic Field Oriented Control)
RFOC (Rotor Field Oriented Control)
-110-
Capitolo5: Azionamenti con motori asincroni
Nelle presenti Note verrà approfondita soltanto la tecnica FAM, la quale prevede di allineare il
flusso rotorico con l’asse d, esattamente come per il controllo “Volt su Hertz” visto in precedenza.
La tecnica di controllo FAM è la tipologia più semplice di controllo vettoriale, realizzata ad anello
aperto. Si ipotizza che il sistema di controllo “funzioni bene” e che sia in grado di far raggiungere
istantaneamente al motore i valori di isd e isq desiderati, cioè si ipotizza che :
(5.79)
i sd i sdrif
i sq i sqrif
per ogni istante di funzionamento.
Si considerino allora come variabili di stato la corrente is ed il flusso r e si rielaborano le
equazioni (5.55) descrittive del modello a 4 parametri al fine di riscriverle in funzione di esse. Si
ottiene:
(5.80)
v s R s i s p s j
s s
L i j
v s R s i s L ks p i s p r j
0 R r i r p r j
s ks s
s r
r
r
Rr
r
r R r i s p r j
is
i r
0
r
r
M
M
s L ks i s r
Da cui:
(5.81)
Rr
v s R S is L ks p is R r is M r j r r js L ks is js r
0 R r R i p j
r
r s
r
r
r
M
,
cioè:
(5.82)
r
v s R S is L ks p is R r is R r M j r r js L ks is js r
p R i R r j
r s
r
r
r
r
M
__
Proiettando entrambe le (5.82) sugli assi d,q, dovendo considerare r solidale con l’asse d ed
osservando dunque che, anche in questo caso, valgono le (5.71), si ottiene:
(5.83)
d :
q :
d :
q :
Rr
L i
r
s ks sq
M
L i
v sq (R s R r ) i sq L ks pi sq
r
r
s ks sd
s r
v sd (R s R r ) i sd L ks pi sd
Rr
r R r i sd p r
M
0 R r i sq
r r
0
-111-
Francesco Della Torre - Azionamenti elettrici
Inoltre risulta:
(5.84)
C n r i sq
Rr
Rr
s r i sq s i sq dt
r
r
Grazie poi alla scelta fatta per l’orientamento degli assi d,q si osserva che, a regime, è p r 0 , ciò
che porge, dalla terza delle (5.83):
(5.85)
r M i sd
Tale relazione mostra che la corrente isd è responsabile del flussaggio della macchina, mentre la
prima delle (5.84) mostra che la corrente isq è responsabile della generazione della coppia, come si
voleva inizialmente. Indicando come “FAM” un blocco descritto dalle (5.83) in cui si impongono le
(5.79), lo schema di controllo che si ottiene è quello rappresentato in Fig.5.27.
Ωrif
Regolato
re
di
velocità
Crif
÷
nΨr
isdrif
n
Campo di
operatività
Ψ
vsd,c
isqrif
FAM
vsq,c
[T2]t
s
va,c
va
vb,c
INV vb
vc,c
vc
1/M
ASIN
3~
Ω
Ψr
n
Ω
Ωmis
H1
Fig.5.27: Controllo FAM del motore asincrono trifase
Un controllo implementato in tale modo presenta due difetti principali:
Forte dipendenza dai parametri del motore asincrono da parte del blocco FAM, il che conferma
quanto anticipato al paragrafo 5.3.5;
Nessun controllo sulle correnti che effettivamente circolano nello statore del motore: infatti, in
base alla (5.83), è necessario “fidarsi” completamente del funzionamento dell’azionamento e
supporre sempre che tali correnti coincidano con i valori di riferimento. Sostanzialmente, si
lavora con il solo anello di velocità chiuso in retroazione, ma gli anelli di corrente (e flusso)
sono aperti.
5.9 Controllo vettoriale indiretto con disaccoppiamento
Trattasi di un evoluzione rispetto al controllo vettoriale appena visto e verrà qui mostrato ancora in
riferimento alla tecnica FAM; si tratta, in sostanza, di chiudere gli anelli di flusso e corrente per
-112-
Capitolo5: Azionamenti con motori asincroni
avere un costante controllo dei parametri di stato ( r ed is ). Si riconsiderino ancora le equazioni
elettromagnetiche (5.55) descrittive della macchina asincrona con modello a quattro parametri, che
qui per comodità si richiamano:
v s R s is p s j
s
s
0 R r i r p r j
r
r
s L ks is r
M i i
s
r
r
(5.86)
Sfruttando la seconda equazione, si rielabori la prima in modo che risulti dipendente dalle sole
variabili di stato, ottenendo:
(5.87)
v s R s is L ks pis R r is
Rr
j
L i j
r j
r r
s ks s
s r
M
Si proietti tale equazione sugli assi d,q tenendo conto, al solito, che per la scelta fatta è:
__
(5.88)
r rd
e che risulta:
(5.89)
j
j
j
r
r
s r
r
Si ottiene in tal modo:
(5.90)
Rr
L i
r
s ks sq
d : v sd (R s R r )i sd L ks pi sd
M
L i
q : v sq (R s R r )i sq L ks pi sq
r
s ks sd
Il controllo che si vorrebbe realizzare è del tipo
disaccoppiato, come indicato in Fig.5.28; in realtà,
osservando le (5.90) appena scritte, ci si accorge che vsq
dipende non solo da isq, ma anche da isd, e lo stesso dicasi
di vsd, che dipende, oltre che da isd, anche da isq. In tal
modo, agendo su vsq si varia anche la isd (e viceversa),
ossia le azioni sugli assi risultano essere accoppiate. Per
avere azioni disaccoppiate le (5.90) sarebbero dovute
essere del tipo:
isdrif
Regolatore vsd,c
di corrente
isd
isqrif
Regolatore vsq,c
di corrente
isq
(5.91)
v sd R tot i sd L ks pi sd
v sq R tot i sq L ks pi sq
Fig.5.28: Anatomia del disaccoppiamento
avendo indicato con:
(5.92)
R tot R s R r
-113-
Francesco Della Torre - Azionamenti elettrici
la resistenza totale. Per risolvere tale problema esistono vari modi; di essi verrà ora qui indicato
quello più intuitivo. In base alle (5.90), è possibile introdurre dei termini di feed-back (precompensazione) che, prelevando mediante misura gli angoli , s , il flusso di rotore, le correnti di
statore e conoscendo i parametri della macchina, consentano di ottenere in uscita delle relazioni del
tipo (5.91). Lo schema che realizza tale operazione (e che sarà poi da inserire nello schema
generale) è rappresentato in Fig.5.29; tale schema sarà sinteticamente indicato con un unico blocco
equivalente, con ingressi ed uscite indicate nella stessa figura. Sfruttando tale accorgimento, lo
schema a blocchi di cui alla Fig.5.27 e relativo alla tecnica FAM “classica” si modifica nello
schema di Fig.5.30; come si vedrà al paragrafo 5.11, tale schema è ancora da modificare in quanto,
nella applicazioni reali, si impiega un unico dispositivo in grado di misurare ψr, s e s .
Rr
r
M
L i
s
ks
sq
isd
vsd,c
isq
vsd,c
vsq,c
v’sd,c
vsq,c
v’sq,c
v’sd,c
Disaccoppia
mento FAM
v’sq,c
s
ψr
L i
s
ks
sd
r
Fig.5.29: Disaccoppiamento FAM realizzato e blocco equivalente
s
Ωrif
Regolato
re
di
velocità
Crif
÷
nΨr
isdrif
n
vsd,c
isqrif
v’
vsq,c Disacc sd,c
FAM s
oppiam
ento
FAM v’sq,c
va,c
[T2]t
vc,c
Ψr
INV vb ASIN
3~
vc
1/M
Campo di
operatività
Ψ
vb,c
va
ψrmis
n
idmis
Ω
iqmis
Ωmis
H1
-114-
Ω
[T2]
iamis
ibmis
icmis
H2
ψr
ia
H3
ib
s
Capitolo5: Azionamenti con motori asincroni
Fig.5.30: Controllo vettoriale FAM con disaccoppiamento per il motore asincrono trifase
5.10 Controllo vettoriale diretto
Tale tipologia di controllo, impiegata nei casi in cui si necessita di frequenze di commutazione
elevate, prevede l’azione diretta sul convertitore a valle del motore asincrono da parte di un
opportuno regolatore di corrente; è essenziale osservare come in tal caso venga sempre impiegato o
un inverter di tipo CSI (Current Source Inverter) oppure di tipo CRPWM, già introdotto in
precedenza, entrambi controllati in corrente. Nel seguito, verranno introdotte brevemente le due
principali tecniche di controllo diretto.
5.10.1 Tecnica a banda d’isteresi (o “bang-bang”)
Lo schema di principio relativo a tale tecnica è rappresentato in Fig.5.31, supponendo di impiegare
un inverter CSI; il regolatore varia le correnti modulanti dell’inverter soltanto quando le differenze
fra le correnti di riferimento e quelle reali fuoriescono da un’opportuna banda, detta banda di
isteresi (cfr. Fig.5.32); in tal modo non si conosce però con esattezza la frequenza di commutazione,
che risulta essere variabile. Inoltre si è fin qui supposto il motore asincrono come un sistema
equilibrato, con conseguenti componenti omopolari nulle, ma con tale tenica potrebbe accadere che
la somma delle correnti iniettate nello statore non sia nulla, ossia che il sistema non sia più, nel
complesso, a simmetria fisica.
Δia
iarif
Δib
ibrif
Δic
icrif
ia,c
Regolatore
Bang-bang
Regolatore
Bang-bang
ib,c
Regolatore
Bang-bang
ic,c
iamis
ibmis
icmis
ia
CSI
ASIN
3~
ib
ic
H1
H2
H3
Fig.5.31: Schema di principio del controllo vettoriale diretto del motore asincrono realizzato mediante
tecnica a banda d’isteresi
Δirif +ε
Δirif
Δirif -ε
Δi
Istante di
commutazione
t
Fig.5.32: Anatomia della tecnica a banda d’isteresi
-115-
Francesco Della Torre - Azionamenti elettrici
5.10.2 Tecnica della banda d’isteresi a pettine
Come già detto, utilizzando la tecnica a banda d’isteresi non si ottiene una frequenza fissa di
commutazione; ciò genera delle subarmoniche nell’alimentazione del motore asincrono, con
conseguente rumore dovuto a battimenti nella macchina stessa. Per ovviare a tale problema è
possibile utilizzare la tecnica a banda d’isteresi a pettine, in cui il controllo sul segnale d’errore
viene eseguito come per la tecnica a banda d’isteresi “classica” ma soltanto in determinati istanti di
tempo, distanti fra loro di un lasso temporale pari al periodo di commutazione (campionamento)
desiderato. In tal modo si ottiene una frequenza di commutazione costante, con conseguente
eliminazione delle subarmoniche.
Δirif +ε
Δirif
Δirif -ε
Δi
tcomm
ta tb
t
Fig.5.33: Anatomia della tecnica a banda d’isteresi a pettine; ta è l’istante di commutazione che si avrebbe
con tecnica “classica”, tb è l’istante di commutazione con tecnica a pettine
5.11 Stimatori ed osservatori di stato
Per realizzare le tecniche di controllo vettoriale viste in precedenza, è necessario poter conoscere,
istante per istante, le seguenti grandezze:
r r
s (Angolo formato dagli assi d,q di Park rispetto agli assi fissi a,b,c)
s (Velocità degli assi d,q di Park rispetto agli assi fissi a,b,c)
(Modulo del flusso rotorico)
In linea teorica tali grandezze sarebbero misurabili direttamente dalla macchina mediante opportuni
trasduttori; in realtà, considerazioni di tipo economico consigliano, in ambito industriale, di
ricavarle da altre grandezze più facilmente (ed economicamente) misurabili, come tensioni, correnti
e velocità meccanica. Per realizzare ciò si impiegano dei dispositivi detti Stimatori di stato se
realizzati in anello aperto ed osservatori di stato se realizzati ad anello chiuso; data la complessità
strutturale e di progettazione di questi ultimi, si è qui scelto di occuparsi soltanto degli Stimatori.
5.11.1 Stimatore VI
Mediante lo stimatore VI è possibile ricavare le grandezze d’interesse a partire dalla misura delle
tensioni e delle correnti statoriche; considerando la Trasformata di Park rispetto ad assi fissi α,β,
l’equazione relativa allo statore della macchina asincrona (la prima delle (5.55)) diviene:
-116-
Capitolo5: Azionamenti con motori asincroni
(5.93)
vs, R s is, ps,
Si noti come, coerentemente con la Teoria di Park, in tale equazione manchi il contributo
mozionale, in quanto scritta, appunto, rispetto ad assi fissi. Note le tensioni di statore e le relative
correnti, è allora possibile scrivere:
(5.94)
p s , v s , R s is , s , ( v s , R s is , )dt
Proiettando tale equazione sugli assi fissi di Park si ottiene:
(5.95)
: s ( v s R s i s )dt
,
: s ( v s R s i s )dt
le quali permettono di ricavare le componenti del flusso di statore. Osservando ora che la terza delle
(5.55), scritta su assi rotanti di Park, vale anche su assi fissi, ossia che risulta:
(5.96)
s, L ks is, r , ,
è possibile ricavare finalmente le componenti del flusso rotorico come:
(5.97)
r , s , L ks i s
r , s , L ks i s
Da tali relazioni sono immediatamente calcolabili il modulo del flusso rotorico e l’angolo s :
(5.98)
r 2r , 2r ,
r ,
, s arcTg
r ,
Inoltre la velocità s è ricavabile come:
(5.99)
d arcTg r ,
s
dt
r ,
p r , r , p r , r ,
2r
In Fig.5.35 viene riportato lo schema a blocchi di tale stimatore. Esso presenta una serie di problemi
e particolarità che è necessario, seppur brevemente, analizzare:
Dalle (5.95) si nota come tutte le grandezze stimate vengano ottenute passando attraverso uno
stadio di integrazione; ciò comporta innanzitutto un ritardo inevitabile nella stima e, di
conseguenza, in tutto il controllo dell’azionamento. In secondo luogo, è necessario osservare che
se il valore della resistenza statorica subisce una qualsiasi variazione (tipicamente dovuta alle
variazioni della temperatura di funzionamento), allora tale variazione verrà anch’essa integrata e
genererà un’incertezza sulla stima stessa. Per ovviare a tale problema, si è soliti impiegare
integratori non puri (funzione di trasferimento 1/s, come in Fig.5.34) bensì del tipo 1/(1+sτ); ciò
significa ridurre la banda di frequenza entro la quale effettivamente avviene l’integrazione (cfr.
Fig. 5.34; la banda effettiva di integrazione è quella in cui la pendenza vale –20 dB/decade).
-117-
Francesco Della Torre - Azionamenti elettrici
Inoltre viene introdotto uno sfasamento pari a π/2, del quale, in alcuni casi, è necessario tener
conto (ovviamente tale sfasamento è introdotto anche con un integratore puro). Il valore corretto
di τ viene, in genere, ricavato mediante
un’opportuna simulazione;
Le
correnti
di
statore
presentano
inevitabilmente dei ripple che si ripercuotono
anche sui valori dei flussi di rotore e, infine,
sulle grandezze da stimare, introducendo, se
non corretti, incertezze di misura addizionali;
La non perfetta conoscenza dei parametri di
macchina (Rs, Lks), soprattutto alla basse
velocità di rotazione, porta ad ulteriori
incertezze che affliggono la stima delle
grandezze.
Tenendo conto di tutti i problemi indicati, si
conclude che lo stimatore di tipo VI è da
impiegarsi preferibilmente nei funzionamenti del
motore asincrono ad alta velocità.
vamis
vbmis
vcmis
iamis
ibmis
icmis
(1/τ)
Fig.5.34: Andamento del diagramma di Bode del
modulo di un integratore ideale (linea
tratteggiata) e di un integratore reale (linea
continua) avente un polo in 1/τ =100 rad/s
vαmis
[T0]
1/s
vβmis
1/s
isαmis
[T0]
ψs,α
ψr,α
ψs,β
ψr,β
Rs
isβmis
Rs
Lks
Lks
s
r ,
arcTg
r ,
ψr,β
ψr,α
ψr,β
|ψr|
2r , 2r ,
ψr,α
X
X
s
s
ψr,β
|ψr|2
ψr,α
X
÷
Fig.5.35: Schema a blocchi dello stimatore VI
-118-
s
Capitolo5: Azionamenti con motori asincroni
5.11.2 Stimatore IΩ
Con questo tipo di stimatore si ottengono le grandezze r r , s e s dalla misura delle
correnti statoriche e della velocità meccanica. Si riconsideri l’equazione su assi rotanti (5.75), che
qui si riporta:
(5.100)
Rr
r R r i sd p r
d : 0
M
)
q : 0 R s i sq (
s
r
Dalla prima di esse si ha, applicando la trasformata di Laplace:
(5.101)
r (s)
Rr
i (s) ,
R r sd
s
M
mentre dalla seconda:
(5.102)
R r i (s)
s
sq
r (s)
n è nota perché Ω è direttamente misurabile ed il numero n di coppie polari è un
La velocità
dato costruttivo, dunque è possibile scrivere:
(5.103)
R
dt
s r i sq
r
E’ necessario conoscere, a partire dalla misura di iabc, le correnti trasformate isd e isq; per effettuare
tale trasformazione serve però s , che è a priori incognito in quanto costituisce proprio una delle
grandezze da stimare; come si rileva facilmente nello schema a blocchi di Fig.5.36, il metodo
impiegato è allora di tipo iterativo: l’angolo s impiegato nel blocco “[T2]” che esegue la
Trasformata di Park su assi rotanti è da intendersi come valore al passo precedente del calcolo
iterativo.
Uno stimatore di questo tipo presenta alcuni problemi:
Al passo k è noto l’angolo s k 1 , dunque vengono calcolate i sd k 1 e i sq k 1 , cioè sono ricavabili le
correnti al passo precedente ma non a quello attuale (trattandosi di un metodo iterativo ciò è del
resto ovvio). Questo aspetto dà problemi in termini di errori di misura, soprattutto alle alte
velocità ;
La non perfetta conoscenza dei parametri della macchina introduce delle inevitabili incertezze
nella stima eseguita; si osservi che, a differenza dello stimatore VI , nello stimatore IΩ entra in
gioco anche la mutua induttanza M, che non è costante ma deve essere rappresentata mediante
un’opportuna curva sperimentale;
Alle alte velocità anche è elevata; dato che il controllo, di qualsiasi genere esso sia, è sempre
implementato con tecniche digitali, è necessario associare il valore di fondo scala al valore
-119-
Francesco Della Torre - Azionamenti elettrici
corrispondente a max , commettendo cosi un errore di risoluzione soprattutto, appunto, alle alte
velocità.
Per tutte queste ragioni si predilige l’uso dello stimatore IΩ alle basse velocità di funzionamento.
iamis
idmis
ibmis
[T2]
iqmis
icmis
Rr
R
s r
M
ψr
Rr/ψr
s
s
Ωamis
mis
n
1/s
s
Fig.5.36: Schema a blocchi dell0 stimatore IΩ
5.11.3 Stimatori combinati
Nella maggior parte delle applicazioni pratiche il campo delle velocità di funzionamento copre sia
le basse che le alte velocità; per quanto detto sopra, allora, si rende necessario l’uso di entrambi gli
Stimatori appena introdotti. Si realizza allora uno stimatore combinato, in cui un’opportuna logica
di controllo commuta, in base alla velocità effettiva, sullo stimatore VI o sullo stimatore IΩ.
E’ opportuno infine far presente che gli schemi di controllo visti in precedenza (in particolare
quelli di Fig.5.27 e Fig.5.30) andrebbero completati con lo stimatore appena introdotto.
iamis
ibmis
icmis
Stimatore
vamis
VI
vbmis
vcmis
ψr
VI
s
Stimatore
IΩ
Ωamis
IΩ
Logica di
commutazione
-120-
s
Capitolo5: Azionamenti con motori asincroni
Fig.5.37: Stimatore combinato
-121-










