f.e.m.

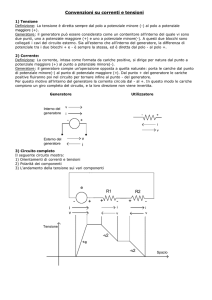
Forza elettromotrice – Estensione della legge di Ohm.
Affinché in un tratto di conduttore omogeneo AB circoli una corrente elettrica stazionaria di intensità I è
necessario che un opportuno dispositivo capace di fornire la d.d.p. VA-VB (generatore), sia collegato agli
estremi A e B del conduttore provvedendo, in un certo senso, a controbilanciare
continuamente l'effetto del movimento delle cariche che tende ad annullare la d.d.p.
stessa. Consideriamo allora un circuito completo (anche se il più semplice che si possa
immaginare) costituito da un conduttore i cui estremi sono collegati, mediante due
morsetti, ad un generatore di d.d.p. costante. Il circuito sia quello rappresentato in Fig.1;
G è il generatore di d.d.p. (potrebbe essere una pila, un accumulatore, un Van der Graaf ),
I è l'intensità di corrente che interessa il circuito.
Il generatore stesso costituisce una porzione dell’intero circuito; esso è caratterizzato da
una resistenza propria r che viene chiamata resistenza interna per distinguerla dalla
Fig.1
resistenza esterna R del resto del circuito.
Ora, se P1 è la potenza dissipata per effetto Joule nell'interno del generatore e P2 quella dissipata nel
circuito esterno si ha, per la legge di Joule:
P1 = r I 2
P2 = R I 2
(1)
per cui la potenza totale dissipata sotto forma di calore è:
P = P1 + P2 = (r + R ) I 2
(2)
Questa potenza è fornita dal generatore G; esso è essenzialmente un dispositivo che trasforma in energia
elettrica energia di altra natura e per questo motivo costituisce un generatore di energia elettrica. I
generatori elettrostatici e le macchine elettriche a funzionamento elettromagnetico (come le dinamo)
convertono in energia elettrica il lavoro meccanico compiuto su di esse da forze di natura non elettrica; le
pile sono dispositivi che convertono in energia elettrica l'energia delle reazioni chimiche che avvengono
in esse; negli effetti termoelettrico e fotoelettrico, che saranno considerati più avanti, si ha conversione di
energia termica e di energia luminosa in energia elettrica.
Nella parte esterna di un circuito l'energia elettrica può essere utilizzata, almeno in parte, per ottenere
nuovamente energia meccanica mediante un motore, o energia chimica, come avviene nella carica di un
accumulatore. Tutte queste trasformazioni tra una forma e l'altra di energia avvengono, ovviamente, con
rendimento minore della unità; infatti una certa frazione dell'energia erogata dal generatore viene
sempre dissipata in calore per effetto Joule. In particolare, se il circuito è puramente ohmico, come è
supposto che sia quello rappresentato in Fig.1, l'energia elettrica erogata dal generatore è interamente
dissipata in calore per effetto Joule (un bilancio energetico più generale potrà essere discusso solo più
avanti) sia nella parte del circuito che comprende il generatore che nella parte esterna.
La potenza P erogata dal generatore di Fig.1 può essere espressa mediante la relazione:
P=EI
(3)
dove la nuova grandezza
P
E = = (r + R ) I
(4)
I
che ha le dimensioni di una d.d.p. e quindi è misurata in volt chiamasi forza elettromotrice (f.e.m.) del
generatore.
Nota - II termine "forza elettromotrice" è quanto mai inopportuno perché questa grandezza non ha,
ovviamente, nulla a che fare con una "forza", nel senso che usualmente si da ad essa in Meccanica. Tale
termine però è ormai entrato nell'uso comune e va accettato.
Applicando la legge di Ohm al conduttore esterno AB di Fig.1 si ha:
VA − VB = R I = E − r I
(5)
Se r è trascurabile rispetto a R, anche r I è trascurabile rispetto a RI e la d.d.p. VA-VB risulta praticamente
uguale alla f.e.m. del generatore; a circuito aperto (I = 0) risulta
VA − VB = E
(6)
ossia: la f.e.m. di un generatore è uguale alla d.d.p. misurata ai suoi morsetti A e B quando esso non
eroga corrente.
1
Essa può essere misurata, per esempio, connettendo i due morsetti del generatore con un elettrometro.
Dalla (5) risulta che se il circuito è chiuso e quindi G eroga corrente, la d.d.p. misurata tra i morsetti A e
B è minore della f.e.m.; infatti, in questo caso, alla corrente di intensità I corrisponde una "caduta di
potenziale" ΔV = r I all'interno di G e quindi la d.d.p. tra i suoi morsetti risulta diminuita di ΔV rispetto
alla f.e.m. E.
Il fatto che a circuito aperto (I = 0) esista una d.d.p. non nulla tra i morsetti A e B del generatore (che è un
conduttore!), sta a significare che in questo sono attive delle forze sotto l'azione delle quali le cariche
assumono una configurazione di equilibrio, caratterizzata da eccesso di cariche positive in A e negative in
G
B. A tale configurazione corrisponde un campo elettrico E , il cui verso va da A a B, e quindi la d.d.p. tra
A e B che si misura con l'elettrometro. Se si collegano i morsetti di G agli estremi di un conduttore
(indicato in Fig.1 con R), in questo si ha movimento di cariche nel verso che va da A a B perché anche in
G
esso è attivo lo stesso campo elettrico E di cui sopra. Tale movimento di cariche tende ad annullare la
d.d.p. tra A e B; ma per effetto delle forze attive nel generatore, in questo prende origine un movimento di
cariche, nel verso che va da B ad A, tale da mantenere la primitiva configurazione di equilibrio
( V A − V B ≠ 0 ) e quindi una corrente elettrica di intensità pari a quella che fluisce nel conduttore esterno
R.
Questa si mantiene finché agisce il generatore e l'energia dissipata, o comunque utilizzata nella parte
esterna del circuito, va a spese dell'energia interna di G o dell'energia che esso, a sua volta, può ricevere
dall'esterno. La corrente elettrica, intesa come “movimento di cariche positive”, fluisce nel conduttore
esterno nel verso che va da A a B e nell'interno del generatore nel verso che va da B ad A; il suo valore è
dato dalla:
I = E / (r + R )
(7)
Ci possiamo ora chiedere quali siano le caratteristiche delle forze attive nel generatore. Fino a questo
G
punto abbiamo sempre supposto che il responsabile del moto delle cariche fosse il campo E . Ma poiché
G
questo è conservativo deve essere C( E ) = 0 (vedi l’appendice!) per una qualsiasi linea chiusa e quindi, in
particolare, per la linea materializzata da un circuito chiuso (generatore più conduttore esterno); ne segue,
per evidenti ragioni energetiche, che il responsabile del moto di insieme delle cariche in un circuito
G
completo non può essere il solo campo E e che quindi in qualche parte del circuito e precisamente nel
generatore, devono essere attive forze di natura non conservativa.
Le considerazioni qualitative appena fatte possono essere precisate quantitativamente nel modo che
segue. Supponiamo che il generatore di f.e.m. non eroghi corrente (circuito aperto); in tal caso una carica
G
G
elettrica q è, nell'interno di G, in equilibrio sotto l'azione di una forza elettrostatica F = q E e di una forza
G
motrice K attiva nel generatore. La condizione di equilibrio è:
G G
(8)
F+K =0
G
G
relazione questa che può sussistere solo se la forza K è essa stessa proporzionale a q, perché E è
G
indipendente dalla carica q su cui agisce. Si può allora scrivere K nella forma
G
G
(9)
K = qE m
G
ed E m chiamasi campo elettromotore. La caratteristica di un generatore è dunque quella di dar luogo
(attraverso meccanismi che variano a seconda dei casi) ad un campo elettromotore; quando non si ha
erogazione di corrente la distribuzione delle cariche nel generatore è configurata in modo da dar luogo ad
G
un campo elettrico statico E tale da soddisfare, sovrapponendosi al campo elettromotore, alla condizione
(8) oppure, tenuto conto della (9), alla:
G
G
(10)
E = − Em
G
Mentre in un semplice conduttore in condizioni di equilibrio E = 0 , in un generatore tali condizioni sono
determinate dalla (10). Se si ammette poi che a caratterizzare un generatore sia essenzialmente il campo
G
G
elettromotore E m e che E m sia indipendente dalla corrente che esso può erogare (circostanza questa che
si verifica nella maggior parte dei casi) si arriva a risultati che sono consistenti con i fatti sperimentali.
2
G
G
G
La situazione è illustrata in Fig.2. E m e E sono in modulo uguali ma hanno versi opposti; E ha il verso
G
che va (come deve essere) dalle cariche positive alle cariche negative; E m ha verso opposto,
essendo dovuto ad esso l'eccesso di cariche positive al morsetto A e l'eccesso di cariche
negative al morsetto B. La natura del campo elettromotore è diversa a seconda del generatore
che si considera; si tratta sempre, comunque, di un campo non conservativo. Il campo
elettromotore è diverso da zero soltanto nel generatore essendo nullo all’esterno.
Nel caso di un circuito completo in cui circoli corrente si ha:
VA − VB = R I = E − r I e quindi essendo VA − VB < E , si ha anche E < E m .
Si noti che a circuito chiuso (I≠0) la d.d.p. V A − V B è sempre minore della f.e.m. erogata dal
Fig.2
generatore. Vale inoltre la pena di sottolineare che mentre la differenza di potenziale V A − V B
G
dipende dal valore della intensità di corrente erogata, la f.e.m. E (ovvero E m ) ne è indipendente,
circostanza questa che effettivamente si verifica almeno nella maggior parte dei casi.
B
A
A
B
Fig.3
In Fig.3 (a) si rappresenta il circuito di Fig.1 sviluppato in linea orizzontale ed in Fig.3(b) è rappresentato
l'andamento del potenziale lungo di esso supponendo il morsetto B del generatore collegato a terra
(VB=0) e trascurabile la resistenza dei conduttori che collegano R al generatore G. Partendo da B e
procedendo da sinistra a destra nel verso della corrente, si incontra il generatore di f.e.m. E dove è attivo il
G
G
campo elettromotore E m . E esprime il lavoro compiuto da E m per unita di carica nel passaggio,
nell’interno di G, delle cariche dai punti a potenziale minore VB a quelli a potenziale maggiore VA; questo
G
lavoro è fatto in parte contro il campo E (all'interno del generatore E m > E ) e per il resto è dissipato
sotto forma di calore nella resistenza interna di G.
G
In A il potenziale è E – r I = V A − V B e le cariche fluendo in R sotto l'azione di E riducono il loro
G
potenziale a zero tornando in B; il lavoro compiuto da E nella resistenza R uguaglia quello compiuto da
G
G
E m (contro E ) nel generatore ed è interamente dissipato sotto forma di calore nella resistenza esterna.
Se si moltiplica la E = r I + R I per la intensità di corrente si ottiene:
E I = r I2 + R I2
Le considerazioni svolte ne chiariscono ulteriormente il significato: il prodotto E I esprime, per
definizione stessa di E la potenza erogata dal generatore; questa è dissipata sotto forma di calore: in r per
un ammontare pari r I 2 ed in R per un ammontare pari a R I 2 .
3
Appendice
4