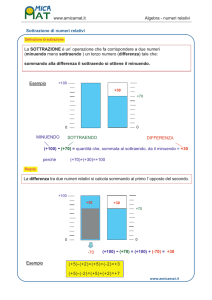
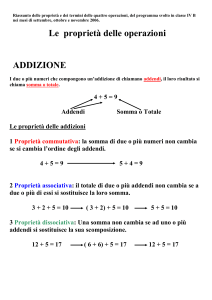
La sottrazione
La differenza di due numeri naturali, col primo numero maggiore o uguale al secondo, è il
numero naturale che addizionato al secondo dà come somma il primo. Nella sottrazione il primo
numero si chiama minuendo, il secondo sottraendo ed il risultato che si ottiene si chiama
differenza. La sottrazione può essere eseguita soltanto quando il minuendo è maggiore o uguale
al sottraendo. Il sottraendo è il numero che deve essere sottratto, il minuendo è il numero di
partenza che deve essere diminuito.
a b c a b c cioè la sottrazione è l’operazione inversa dell’addizione.
a si chiama minuendo, b si chiama sottraendo, c si chiama differenza.
Nella sottrazione lo zero lascia invariato il minuendo solo se esso rappresenta il
sottraendo. Infatti la sottrazione non gode della proprietà commutativa.
La sottrazione gode della proprietà invariantiva che afferma quanto segue: se aggiungo o
sottraggo uno stesso numero al minuendo e al sottraendo la differenza non
cambia.
Proprietà invariantiva: a b a x b x a x b x
Eseguire sottrazioni in colonna con due cambi
La sottrazione con il cambio o prestito presenta delle difficoltà perché implica una notevole capacità
di astrazione. Analizziamo la sottrazione con due cambi:
651-182=469 utilizzando la seguente
tabella:
Iniziamo l’operazione partendo dalla colonna delle unità. Poiché non è possibile togliere 2 unità da
1 unità, si trasforma una delle 5 decine del numero 651 in 10 unità che si aggiungono alle unità
del minuendo che diventano 11. Da queste 11 unità togliamo le 2 unità del sottraendo e rimangono
9 unità della differenza. Si passa alla colonna delle decine e, poiché dalle 4 decine rimaste non è
possibile toglierne 8 , si trasforma 1 centinaio del numero 651 con 10 decine che diventano 14 ;da
queste se ne tolgono 8 e restano solo 6 decine della differenza. Infine dalle 5 centinaia si sottrae 1
centinaio del sottraendo; rimangono solo 4 centinaia della differenza.
Adesso effettuiamo la stessa sottrazione incolonnando i numeri in modo che ogni cifra sia collocata
secondo il suo valore posizionale per cui le unità sono sempre incolonnate sotto le altre unità,
le decine sotto le altre decine, le centinaia sotto le altre centinaia e così di seguito.
La sottrazione 1 2 non è possibile. Allora l’ 1 si fa prestare 1 decina e
h da u
diventa 11 unità. 11 2 9 . Rimangono 4 decine; 4 8 non è possibile. Il 4
6
1
4
5
si fa prestare 1 centinaio e diventa 14 decine. 14 8 6 . Rimangono 5
centinaia. 5 1 4 .
5
8
6
14
1
2
9
1
Nel seguente esempio 201147 55 , che è una sottrazione con doppio cambio, non si possono
prendere in prestito le decine perché c’è lo zero. Si procede come segue:
(1) Si prende in prestito un centinaio così da avere 10 decine
h
da
(2) Si lasciano 9 decine nella colonna delle decine e si porta 1 decina nella
1
2
1
//
9
colonna delle unità
(3) Adesso è possibile effettuare la differenza tra le unità, le decine, le centinaia.
0
4
5
u
2
7
5
1
Eseguire la prova della sottrazione
Per verificare l’esattezza della differenza di due numeri basta ricordare che la sottrazione è
l’operazione inversa dell’addizione. Infatti noi sappiamo che la differenza tra due numeri è quel
numero naturale che sommato al sottraendo dà come risultato il minuendo.
643 412 231
6 4 3
2 3 1
4 1 2
prova 4 1 2
2 3 1
6 4 3