2
Edutecnica.it – Esercizi sui filtri attivi
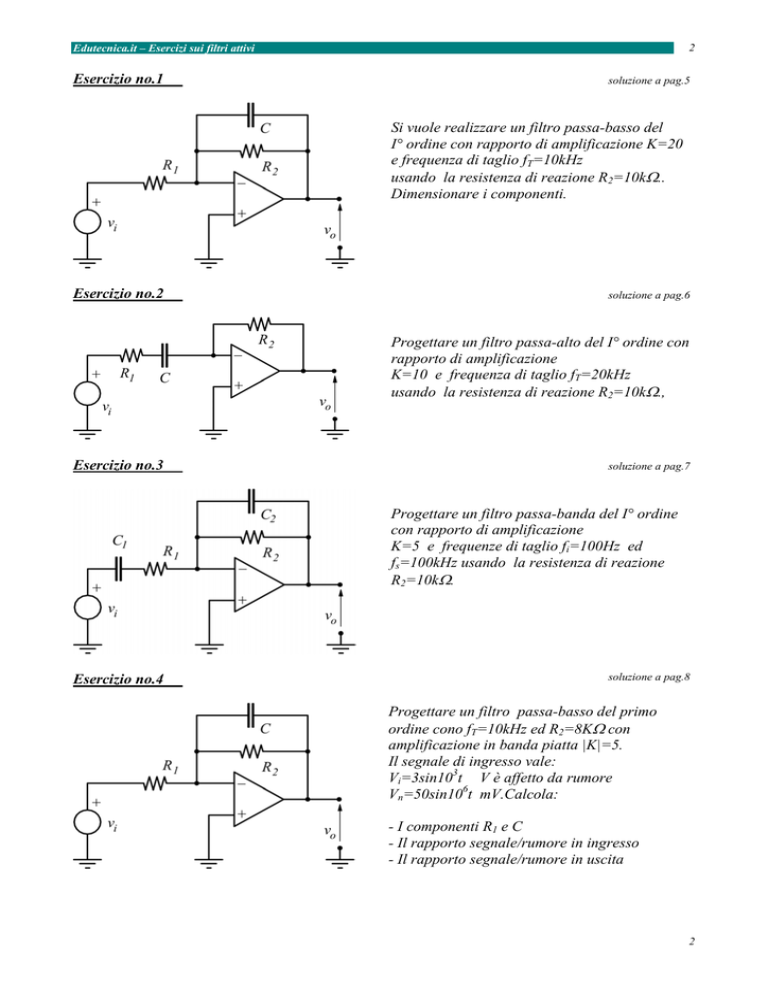
Esercizio no.1
▄
soluzione a pag.5
Si vuole realizzare un filtro passa-basso del
I° ordine con rapporto di amplificazione K=20
e frequenza di taglio fT=10kHz
usando la resistenza di reazione R2=10kΩ..
Dimensionare i componenti.
Esercizio no.2
▄
soluzione a pag.6
Progettare un filtro passa-alto del I° ordine con
rapporto di amplificazione
K=10 e frequenza di taglio fT=20kHz
usando la resistenza di reazione R2=10kΩ.,
Esercizio no.3
▄
soluzione a pag.7
Progettare un filtro passa-banda del I° ordine
con rapporto di amplificazione
K=5 e frequenze di taglio fi=100Hz ed
fs=100kHz usando la resistenza di reazione
R2=10kΩ.
Esercizio no.4
▄
soluzione a pag.8
Progettare un filtro passa-basso del primo
ordine cono fT=10kHz ed R2=8KΩ con
amplificazione in banda piatta |K|=5.
Il segnale di ingresso vale:
Vi=3sin103t V è affetto da rumore
Vn=50sin106t mV.Calcola:
- I componenti R1 e C
- Il rapporto segnale/rumore in ingresso
- Il rapporto segnale/rumore in uscita
2
3
Edutecnica.it – Esercizi sui filtri attivi
Esercizio no.5
▄
soluzione a pag.9
Progettare un filtro passa-bassi di
Butterworth con circuito a retroazione
multipla con frequenza di taglio fT=1kHz
ed amplificazione in banda |K|=12
con il condensatore C2=1 nF.
Esercizio no.6
▄
soluzione a pag.9
Nel filtro passa-alto VCVS si ha
R1=R2=R=10kΩ;
RA=22kΩ.
C1=C2=C=10nF.
Calcola RB in modo che venga
soddisfatta la condizione di
Butterworth.
Calcola, inoltre, la frequenza di taglio
del filtro.
Esercizio no.7
▄
soluzione a pag.10
Progettare un filtro passa-banda con pulsazioni ti taglio ω i=102r/s e ω s=105r/s con guadagno a
centro banda di 40dB, usando due filtri (passa-basso e passa-alto) a reazione multipla, disposti in
cascata.
3
4
Edutecnica.it – Esercizi sui filtri attivi
Esercizio no.8
▄
soluzione a pag.11
Progettare un filtro passa-basso a retroazione multipla alla Chebyshev con ξ=0,2.
Si vuole una amplificazione in banda piatta K=10 con pulsazione naturale ωn=125,6krad/s.
Assumere C2=1nF. Calcolare:
- Tutti i restanti componenti
- L’amplificazione massima |T(jω)|max in corrispondenza del picco di risonanza.
Esercizio no.9
▄
soluzione a pag.11
Calcola il guadagno e la frequenza di taglio di un filtro attivo passa-basso a retroazione multipla,
sapendo che:
R1=21kΩ
R2=1,2kΩ
Esercizio no.10
▄
R3=0,21MΩ C1=0,1 µF
C2=1 nF
soluzione a pag.12
Determina la funzione di trasferimento di un filtro passa-basso alla Butterworth con guadagno
12dB e frequenza di taglio fT=2000Hz.
4
5
Edutecnica.it – Esercizi sui filtri attivi
Esercizio no.1
Si vuole realizzare un filtro passa-basso del
I° ordine con rapporto di amplificazione K=20
e frequenza di taglio fT=10kHz
usando la resistenza di reazione R2=10kΩ.
Esercizio no.1:soluzione
Dal circuito illustrato si ricava:
T( s ) = −
1
1
sC = − R2 ⋅
R1
R1 ( 1 + sCR2 )
R2 //
T ( jω ) = −
in regime sinusoidale
R2
1
⋅
R1 ( 1 + jωCR2 )
la frequenza di taglio si ha in corrispondenza dell’unico polo:
jω = −
1
1
1
→ | ωT |=
→ f T =
R2 C
R2 C
2π R2 C
C=
1
1
=
= 1,59 nF
2π R2 f T 2π 10 4 ⋅ 10 4
K=
R2
R1
→ R1 =
da cui
dato che
R2 10
=
= 0 ,5 kΩ
K 20
5
6
Edutecnica.it – Esercizi sui filtri attivi
Esercizio no.2
Progettare un filtro passa-alto del I° ordine con
rapporto di amplificazione
K=10 e frequenza di taglio fT=20kHz
usando la resistenza di reazione R2=10kΩ.,
Esercizio no.2:soluzione
Dal circuito si ricava:
R2
T( s ) = −
R1 +
quindi K =
R2
R1
1
sC
=−
sR2 C
RC
s
→ | T ( s ) |= 2
1 + sR1C
R1C ( s + 1 / R1C )
→ R1 =
R2 10
=
= 1 kΩ
K 10
la frequenza di taglio, coincide con la frequenza del polo
| ωT |=
1
questa formula ci permette di calcolare il condensatore
R1C
2π f T =
1
1
1
→ C =
=
= 8 nF
R1C
2π f T R1 2π 20 ⋅ 10 310 3
6
7
Edutecnica.it – Esercizi sui filtri attivi
Esercizio no.3
Progettare un filtro passa-banda del I° ordine
con rapporto di amplificazione
K=5 e frequenze di taglio fi=100Hz ed
fs=100kHz
usando la resistenza di reazione R2=10kΩ.
Esercizio no.3:soluzione
Abbiamo già visto come la funzione di trasferimento sia:
T( s ) = K
ω ss
( s + ω i )( s + ω s )
ω i = 2π 100 = 614 r / s
ω s = 2π 10 5 = 6 ,14 ⋅ 10 5 r / s
ωs =
1
C2 R2
K=
R2
10
10
→ 5=
→ R1 =
= 2 kΩ
R1
R1
5
ωi =
1
R1C1
→ C2 =
1
1
= 4
= 0 ,16 ⋅ 10 − 9 F = 0 ,16 nF = 160 pF
5
ωs R2 10 ⋅ 6 ,14 ⋅ 10
→ 614 =
1
2000 ⋅ C1
→ C1 =
1
= 7,95 ⋅ 10 -7 F = 795 nF
2000 ⋅ 614
7
8
Edutecnica.it – Esercizi sui filtri attivi
Esercizio no.4
Progettare un filtro passa-basso del primo
ordine con frequenza di taglio fT=10kHz e
resistenza di reazione R2=8KΩ con
amplificazione in banda piatta |K|=5.
Il segnale di ingresso vale:
Vi=3sin103t
V
è affetto da rumore
Vn=50sin106t mV
Calcola:
I componenti R1 e C
Il rapporto segnale/rumore in ingresso
Il rapporto segnale/rumore in uscita
Esercizio no.4:soluzione
Abbiamo già visto che la frequenza di taglio vale:
fT =
| K |=
1
1
1
→ 10 4 =
→ C =
= 2 nF
3
2π R2 C
2π 8 ⋅ 10 C
2π 8 ⋅ 107
R2
R1
→ 5 =
10 4
R1
→
R1 =
10 4
= 2 kΩ
5
3
S
= 60
=
N in 50 ⋅ 10 − 3
All’ingresso il rapporto segnale/rumore:
Per tale rapporto calcolato in uscita bisogna considerare che ωT = 2π ⋅ f T = 62831 r/s
si nota come sia ωT < 10 6 quindi, il rumore non viene pienamente amplificato (la frequenza di
rumore è ben oltre la frequenza di taglio).
| T ( jω ) |=
R2
1
⋅
R1 1 + ( ω R C )2
2
Vo = KVi = 5 ⋅ 3 = 15 V
→ | T ( j10 6 ) |=
5
6
3
1 + ( 10 8 ⋅ 10 2 ⋅ 10
−9 2
)
= 0 ,313
Vno = 0 ,313 ⋅ Vni = 0 ,313 ⋅ 50 ⋅ 10 −3
V
15
S
= 957
= o =
N o Vno 0 ,313 ⋅ 50 ⋅ 10 − 3
L’uso del filtro ha prodotto, oltre che l’amplificazione del segnale anche un netto miglioramento
del rapporto segnale/rumore.
8
9
Edutecnica.it – Esercizi sui filtri attivi
Esercizio no.5
Progettare un filtro passa-bassi di Butterworth
con circuito a retroazione multipla con
frequenza di taglio fT=1kHz
ed amplificazione in banda |K|=12
con il condensatore C2=1 nF.
Esercizio no.5:soluzione
La condizione di Butterworth impone: ξ =
ωn = 2π ⋅ fT = 6283 r / s
R3 =
R2 =
1
2QωnC2
=
1
1
=
2Q
2
1
= 112,5 kΩ
6283 ⋅ 10 − 9 2
R1 =
applicando le formule di progetto:
R3 112 ,5
=
= 9,3 kΩ
|K|
12
R3
112 ,5
=
= 8,6 kΩ
| K | +1
13
Esercizio no.6
Nel filtro passa-alto VCVS si ha
R1=R2=R=10kΩ;
RA=22kΩ.
C1=C2=C=10nF.
Calcola RB in modo che venga
soddisfatta la condizione di
Butterworth.
Calcola, inoltre, la frequenza di taglio
del filtro.
Esercizio no.6:soluzione
Usando le formule di progetto:
3−K
2
→ K = 3 − 2ξ
→ K = 3 −
= 1,586
2
2
R
K = 1+ B
→ RB = KR A − RA = RA ( K − 1 ) = 0 ,586 RA = 12 ,89 kΩ
RA
ξ=
La frequenza di taglio del filtro:
ωn =
ω
1
1
= 4
= 10 4 r / s
→ fT = n = 1591,5Hz = 1,59 kHz
−8
RC 10 ⋅ 10
2π
9
10
Edutecnica.it – Esercizi sui filtri attivi
Esercizio no.7
Progettare un filtro passa-banda con pulsazioni ti taglio ω i=102r/s e ω s=105r/s con guadagno a
centro banda di 40dB, usando due filtri (passa-basso e passa-alto) a reazione multipla, disposti in
cascata.
Esercizio no.7:soluzione
Come si vede in figura, abbiamo, prima un filtro passa-alto la cui pulsazione di taglio ωT=ωi del
filtro passa-banda.
In cascata ad esso, viene disposto un filtro passa-basso la cui pulsazione di taglio ωT=ω s.
Per entrambi i filtri, riteniamo valida la condizione di Butterworth ξ =
1
1
=
2Q
2
Ovviamente i guadagni dei due stadi saranno identici e pari a
| G |dB = 40 dB = 20 lg G
→ G = K1 ⋅ K 2 = 100
→ K1 = K 2 = K = 10
questo è quello che avviene a centro banda.
per il primo stadio, passa-alto:
ωn = ω i = 10 2 r / s K1 = 10
C3 =
C1
= 68 nF
| K1 |
ξ=
R1 =
1
ponendo C1=C2=680nF dalle formule di progetto:
2
1
1
⋅ C1
Qωn 2 +
| K1 |
= 9 ,9 kΩ
R2 = 218 kΩ
per il secondo stadio, passa-basso:
ωn = ω s = 10 5 r / s K 2 = 10
R30 =
R20 =
1
2QωnC20
= 7 ,09 kΩ
R30
= 0 ,644 kΩ
| K 2 | +1
ξ=
R10 =
1
ponendo C20=1 nF dalle formule di progetto:
2
R3
= 0 ,709 kΩ
| K2 |
C10 = 4C20Q 2 ( | K 2 | +1 ) = 22 nF
10
11
Edutecnica.it – Esercizi sui filtri attivi
Esercizio no.8
Progettare un filtro passa-basso a retroazione multipla alla Chebyshev con ξ=0,2.
Si vuole una amplificazione in banda piatta K=10 con pulsazione naturale ωn=125,6krad/s.
Assumere C2=1nF. Calcolare:
- Tutti i restanti componenti
- L’amplificazione massima |T(jω)|max in corrispondenza del picco di risonanza.
Esercizio no.8:soluzione
Usando le formule di progetto:
C1 = 4C2Q 2 ( | K | +1 ) = 1,76 nF
R1 =
R3 =
R3
= 1,99 kΩ
|K|
R2 =
dalle formule, poi risulta: | T ( jω ) | max =
1
2QωnC2
= 19 ,9 kΩ
R3
= 1,8 kΩ
| K | +1
K
2ξ 1 − ξ 2
= 25 ,5
questo massimo si ha in corrispondenza della frequenza f M = f n 1 − 2ξ 2 = 19 ,18 kHz
dove f n =
ωn
= 20 kHz
2π
Esercizio no.9
Calcola il guadagno e la frequenza di taglio di un filtro attivo passa-basso a retroazione multipla,
sapendo che:
R1=21kΩ
R2=1,2kΩ
R3=0,21MΩ C1=0,1 µF
C2=1 nF
Esercizio no.9:soluzione
Dalle formule K = −
1 C2 R2
+
ξ=
2 C1 R3
dato che ξ =
R3
210
=−
= −10
R1
21
R3
+
R2
R2 R3
R1
1 10 − 9 1,2
210
210 ⋅ 1,2
=
= 0 ,707
+
+
2 10 −7 210
1
,
2
21
1
il filtro è a banda piatta.
2
11
Edutecnica.it – Esercizi sui filtri attivi
12
Esercizio no.10
Determina la funzione di trasferimento di un filtro passa-basso alla Butterworth con guadagno
12dB e frequenza di taglio fT=2000Hz.
Esercizio no.10:soluzione
Stavolta il guadagno è espresso in dB.
12 = 20lgK
→ K = 1012 / 20 = 3 ,98
1
= 0 ,707
2
K ⋅ ω n2
la funzione di trasferimento per un LPF di II° ordine è T ( s ) = 2
per cui
s + 2 sξω n + ω n2
ωn = 2π ⋅ fT = 2π ⋅ 2000 = 12566 rad / s mentre ξ =
T( s ) =
628,47 ⋅ 106
s 2 + 0 ,0177 ⋅ 106 s + 157,9 ⋅ 106
12









