Moto lungo un piano
inclinato
Si abbia un punto materiale di massa M che
scivola lungo un piano inclinato privo di
attrito, la cui lunghezza sia l e la cui altezza
sia h. Sul corpo, nella ipotesi in cui si possa
trascurare la resistenza dell’aria, agiscono
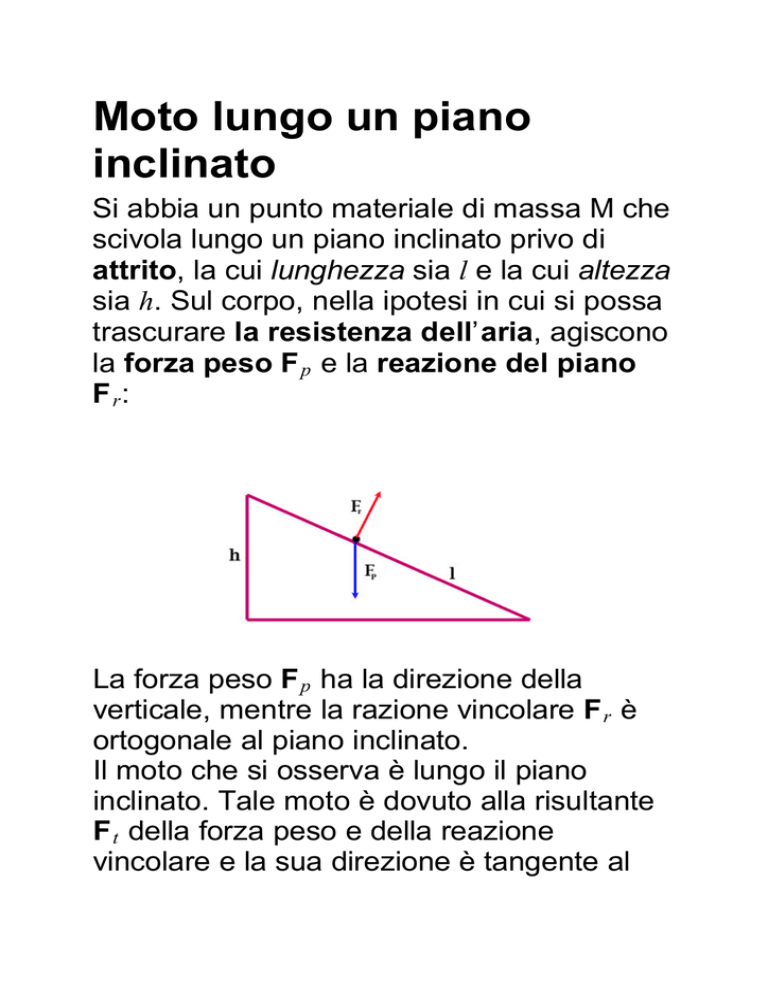
la forza peso F p e la reazione del piano
Fr:
La forza peso F p ha la direzione della
verticale, mentre la razione vincolare F r è
ortogonale al piano inclinato.
Il moto che si osserva è lungo il piano
inclinato. Tale moto è dovuto alla risultante
F t della forza peso e della reazione
vincolare e la sua direzione è tangente al
piano inclinato:
L’intensità della reazione vincolare del piano
può esprimersi in termini della forza peso.
Dal precedente grafico si vede che
l’intensità della reazione vincolare è uguale
e di segno contrario alla componente
normale, F n della forza peso:
Calcoliamo esplicitamente l’intensità della
forza risultante F t , responsabile del moto
del corpo.
Possiamo valutare l’intensità della forza
F t usando la similitudine tra i triangoli ABC e
DEF.
Avremo
DF : CB = DE : CA
ovvero
Mg : l = F t : h
da cui
Mgh
l
Scegliendo l’asse x come indicato in Figura,
Ft =
possiamo utilizzare l’equazione del moto
di un punto materiale e scrivere
gh
Ma x = M
l
Il punto materiale, durante la sua discesa, si
muove con una accelerazione costante
gh
ax =
l
L’accelerazione non dipende dalla massa
del corpo, come i corpi in caduta libera.
Poiché l è maggiore di h l’accelerazione di
un punto materiale, lungo un piano
inclinato, è inferiore all’accelerazione di un
corpo in caduta libera. Essa è inferiore di un
fattore h/l .
Nota l’accelerazione di un punto materiale,
si può risalire dal diagramma
accelerazione-tempo alla velocità
posseduta dal punto materiale nel corso del
tempo e poi dal diagramma
velocità-tempo ottenere lo spazio percorso
da esso.
Se il punto materiale, parte al tempo t = 0
con velocità nulla, dal diagramma
accelerazione-tempo (porre nel grafico
g=gh/l)
troviamo che la velocità lungo l’asse x è
gh
v x Ýt Þ =
t
1
l
mentre dal diagramma velocità-tempo
(porre nel grafico g=gh/l)
abbiamo lo spazio percorso:
gh 2
1
t
2
xÝt Þ =
2
l
Quando il punto materiale arriva alla fine del
piano inclinato, avrà percorso il tratto l; il
tempo, t l , impiegato dal punto materiale per
percorrere l’intero piano inclinato, si otterrà
dalla (2) ponendo x = l:
gh 2
tl
l= 1
2
l
Risolvendo rispetto a t l , otteniamo
l th
=
3
t l = l 2h
h g
h
dove abbiamo introdotto, il tempo t h ,
impiegato da un punto materiale, in caduta
libera, a cadere da un’altezza h.
Il tempo che impiega un punto materiale a
scendere tutto il piano inclinato è l/h volte
più grande del tempo che impiega un corpo
a cadere, in caduta libera da un’altezza h.
Il risultato (3), come il tempo nella caduta
libera, non dipende dalla massa del punto
materiale, quindi non dipende dal corpo.
Possiamo dire che tutti i corpi,
approssimabili a dei punti materiali che,
partendo dalla sommità di un piano
inclinato, privo di attrito, scivolano lungo lo
stesso piano inclinato, se si trascura la
resistenza dell’aria, impiegano lo stesso
tempo ad arrivare alla fine del piano
inclinato.
La velocità che possiede un qualunque
punto materiale quando arriva alla fine del
piano inclinato, si ottiene sostituendo il
valore di t l , dato dalla (3), nell’equazione
(1):
gh l 2h
vÝt l Þ =
= 2gh
4
g
l h
La velocità di arrivo alla fine del piano
inclinato è uguale alla velocità di arrivo al
suolo di un qualunque punto materiale che
cade in caduta libera da una altezza h.












