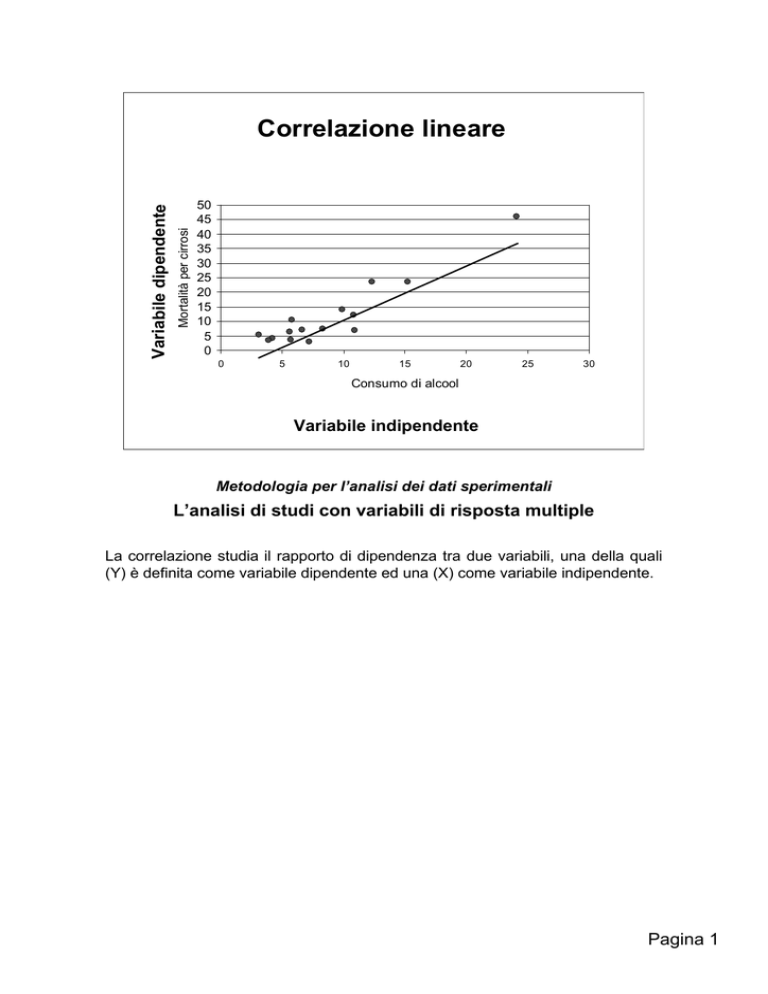
Mortalità per cirrosi
Variabile dipendente
Correlazione lineare
50
45
40
35
30
25
20
15
10
5
0
0
5
10
15
20
25
30
Consumo di alcool
Variabile indipendente
Metodologia per l’analisi dei dati sperimentali
L’analisi di studi con variabili di risposta multiple
La correlazione studia il rapporto di dipendenza tra due variabili, una della quali
(Y) è definita come variabile dipendente ed una (X) come variabile indipendente.
Pagina 1
Correlazione lineare
• Viene utilizzata quando si voglia valutare la
relazione lineare tra due o più variabili
• Viene di solito rappresentata come
diagramma di dispersione sul piano
cartesiano
• La correlazione significativa tra due variabili
NON IMPLICA NECESSARIAMENTE un
nesso di casualità
Pagina 2
Coefficiente di correlazione lineare
r=0.60
r=1
r=0
Il coefficiente di correlazione lineare r è una misura di associazione tra due
variabili che variano in modo congiunto. Il valore di r varia tra -1 (correlazione
negativa perfetta) a 0 (assenza totale di correlazione ad 1 (correlazione positiva
perfetta).
Pagina 3
Coefficiente di correlazione lineare
∑ x∑ y
(xi − x )(yi − y ) ∑ (xy ) − n
∑
COV (x, y ) =
=
(n − 1)
(n − 1)
r=
∑ (x − x )(y − y )
∑ (x − x ) (y − y )
i
i
2
i
2
i
=
( x )( y )
∑ xy − ∑ n∑
( x ) y² − (∑ y )
∑ x² − ∑
∑
n
n
2
2
Pagina 4
Coefficiente di correlazione lineare
La statistica:
t=
r ⋅ n−2
1− r 2
è distribuita come t di Student con (n-2) gradi di libertà
Pagina 5
Y
50
45
40
35
30
25
20
15
10
5
0
0
5
10
15
20
25
30
X
Il metodo matematico per individuare la retta di regressione è il metodo dei
minimi quadrati, che minimizza la somma degli scarti quadratici tra y osservata
ed y attesa.
Pagina 6
Y
Funzione lineare
50
45
40
35
30
25
20
15
10
5
0
0
5
10
15
20
25
30
X
ŷ i = b 0 + b1x i
Pagina 7
Correlazione lineare
y = b0 + b1x
b1 =
COD(x, y )
=
DEV (x )
∑ xi yi − ∑
xi ∑ yi
n
2
(
xi )
∑
2
∑ xi − n
b0 = y - b1x
Pagina 8
Scomposizione della devianza
DEV(y ) = ∑ (y i − y )
2
(y i − y ) = y i − ŷ i + ŷ i − y = (y i − ŷ i ) − (ŷ i − y )
∑ (y
− y ) = ∑ (ŷ i − y ) + ∑ (y i − ŷ ) + 2∑ (ŷ i − y )(y i − ŷ i )
2
2
i
∑ (y
2
− y ) = ∑ (ŷ i − y ) + ∑ (y i − ŷ )
2
2
i
SS(b1)
devianza
DOVUTA alla
regressione
2
SS(e)
devianza
RESIDUA
Ma la regressione può essere analizzata come un modello di analisi della
varianza. L’analisi è concettualmente simile a quella dell’ANOVA ad un criterio di
classificazione.
Pagina 9
Devianza dovuta alla regressione
[∑ (x − x )(y − y )] = [COD(x, y )]
SS(b ) =
2
i
1
∑ (x
i
− x)
2
i
2
DEV (x )
∑ x∑ y
∑ (xy ) −
n
=
2
( x)
∑ x 2 − ∑n
2
Pagina 10
ANOVA applicata alla regressione
Fonte di
variazione
SS
g.l.
MS
Regressione
SS(b1)
1
MS(b1)
Residuo
Per
differenza
n-2
MS(e)
TOTALE
SS(y)
n-1
Pagina 11
A differenza degli studi che riportano media e deviazione standard delle variabili
di risposta, quelli che descrivono i dati come regressione sono difficilmente
ricostruibili a partire dai risultati.
Utilizziamo quindi i risultati di un esempio di Armitage, che descrivono un gruppo
di lavoratori dell’industria del cadmio, esposti da più di 10 anni.
Pagina 12
6
5
4
3
2
1
0
35
40
45
50
55
60
65
70
La rappresentazione grafica ci lascia intuire la possibilità di una relazione inversa
tra le variabili.
Analizzare graficamente i risultati è una pratica utile, prima di procedere
all’analisi, perché consente di individuare outliers (punti molto scostati dai
rimanenti) ed influence points (punti che da soli influenzano la direzione della
retta.
E’ corretto verificare l’esattezza di questi dati, ma non eliminarli per le loro
caratteristiche.
Pagina 13
Pagina 14
Agli elementi di calcolo per le formula semplificate che abbiamo utilizzato per una
singola varriabile, SOMMA(x) e SOMMA.Q(x) diviene necessaria la somma dei
prodotti. E’ conveniente generare la colonna dei prodotti xy e calcolarne la
sommatoria.
Pagina 15
xy −∑ ∑
COD(x, y ) ∑
n
=
=
(
)
DEV x
( x)
∑x − ∑
xi
i
b1
i
2
2
i
=
yi
=
i
n
− 77.642
= −0.085
912.25
b0 = y - b1x =
=
47.39
597
− − 0.085 ⋅
= 8.183
12
12
Pagina 16
6
5
4
3
2
1
0
35
40
45
50
55
60
65
70
La retta stimata è effettivamente indicativa di una relazione inversa. La
rappresentazione della retta è effettuata correttamente solo entro i limiti di valori
di x presenti nella regressione.
Pagina 17
∑ x∑ y
∑ (xy ) −
n
=
=
2
(
x
)
∑ x 2 − ∑n
2
SS(b1 ) =
=
[COD(x, y )]2
DEV (x )
[ −77.6425] 2
= 6.608
912.25
La devianza dovuta alla regressione si calcola a partire dagli stessi termini.
Pagina 18
ANOVA applicata alla regressione
Fonte di
variazione
SS
g.l.
MS
Regressione
6.608
1
MS(b1)
Residuo
Per
differenza
n-2
MS(e)
TOTALE
11.739
n-1
Pagina 19
ANOVA applicata alla regressione
Fonte di
variazione
SS
g.l.
MS
Regressione
6.608
1
6.608
Residuo
5.131
10
0.513
TOTALE
11.739
11
Pagina 20
ANOVA applicata alla regressione
Il rapporto:
F=
MS(b1 )
MS(e )
segue la distribuzione F con 1 ed (n-2) gradi di libertà
Pagina 21
ANOVA applicata alla regressione
Fonte di
variazione
SS
g.l.
MS
Regressione
6.608
1
6.608
Residuo
5.131
10
0.513
TOTALE
11.739
11
F=12.87
Il valore di F consente di rifiutare l’ipotesi nulla ad un livello di significatività di
0.0049
Pagina 22
Pagina 23
Intervallo di confidenza del
coefficiente angolare
L'errore standard del coefficiente angolare è:
sb1 =
MS(e)
SS(x)
Per cui il suo intervallo di confidenza è:
b1 ± tα ⋅ sb1
Pagina 24
b1 ± tα ⋅ sb1 = −0.085 ± 2.228 ⋅ 0.0237 = −0.032 ÷ −0.137
Pagina 25
Intervallo di confidenza
della stima di y
L'errore standard di
ŷ
è:
SS(e) 1 ( x i − x)2
s yi =
⋅ 1+ +
(n - 2) n SS(x)
Per cui il suo intervallo di confidenza è:
yˆ i ± tα ⋅ sy
i
Pagina 26
Pagina 27
Coefficiente di determinazione
La quota di variazione della Y attribuibile alla associazione
lineare con la x è valutata come:
r2 =
SS(b1 )
SS(y )
Questo rapporto, riferito come coefficiente di determinazione, varia da
0 ad 1:
- è 0 quando tra le variabili non c'è associazione lineare
- è 1 quando tutta la variazione della y è determinata dalla relazione
lineare con la x.
Pagina 28
Analisi della covarianza
• L’analisi della covarianza (ANCOVA) è
adatta all’analisi di dati in cui la variabile
oggetto di studio è influenzata da cause
sistematiche, ed associata ad una
covariata per la quale sia difficile
formare gruppi omogenei
Pagina 29
Analisi della covarianza
yy
yy
yy
xx
xx
xx
Pagina 30
L’esempio riporta i dati di lavoratori dell’industria del candmio, rispettivamente
esposti da più di 10 anni, esposti da 10 anni, e non esposti.
Pagina 31
Abbiamo già visto come le misure di sintesi, somme, somme dei quadrati e
somme dei prodotti, contengano tutta l’informazione che ci sarà necessaria.
Pagina 32
∑ ∑
xy −
∑
COD(x, y )
n
=
=
DEV (x )
( x)
∑x − ∑
xi
i
bcom
i
2
2
i
i
yi
==
− 183.623
= −0.0195
9392.123
n
Il beta comune (cioè il coefficiente di regressione che tiene conto di tutti i dati,
trascurando la loro divisione in gruppi) si calcola a partire dalle somme delle
devianze e delle codevianze dei tre gruppi.
Pagina 33
F=
MSparallelismo
MSresidua entro gruppi
• Consente di rifiutare l’ipotesi di parallelismo tra i
gruppi.
• Se il test non è significativo i dati non mostrano
eterogeneità dovuta a mancato parallelismo, e si può
rappresentare la relazione tra X e Y con il coefficiente
di regressione comune
• Se non si rifiuta l’ipotesi di parallelismo, può essere
condotta l’analisi della covarianza
Pagina 34
Un problema dell’analisi della covarianza è che alcuni software, anche piuttosto
avanzati, quali STATA o SAS, non hanno un programma specifico per eseguirlo,
ma richiedono l’uso di artifici di calcolo.
Nell’esempio STATA: l’assenza di interazione è indicativa di parallelismo.
Pagina 35
Il termine può quindi venire rimosso dall’analisi. Non risulta alcuna differenza tra i
gruppi; le differenze sono tutte spiegate dall’età.
Pagina 36
Variabile
Esposti >
10 anni
Esposti <
10 anni
Non
esposti
Età
49.8±9.1
37.8±9.2
39.8±12
CV
3.94±1.03
4.47±0.68 4.46±0.69
CV “aggiustata”
3.77
4.52
4.48
y i* = y i − b1c (x i − x)
L’ANCOVA consente il calcolo delle medie “aggiustate”, cioè di quelle che
sarebbero state le medie delle y se il valore delle x fosse stato uguale in tutti i
gruppi, e pari al valore di x medio. Il cacolo è molto semplice, anche quando il
software a disposizione non lo effettui (sono denominate anche LS means)
Pagina 37
Un uso improprio della correlazione
Strumento 2
700
600
500
400
300
200
100
0
0
200
400
600
800
Strumento 1
Viene spesso utilizzata in modo improprio la correlazione per definire la
concordanza di due metodi o due strumenti di misura.
La correlazione significa la presenza di dipendenza tra le misure, ma è difficile
immaginare che due misure della stessa unità sperimentale siano indipendenti!
Pagina 38
Una presentazione alternativa
80
80
60
60
Differenza tra
tra le
le due
due misure
misure
Differenza
40
40
20
20
00
-20
-20
00
200
200
400
400
600
600
800
800
-40
-40
-60
-60
-80
-80
-100
-100
PEFR
PEFR me
medio
dio
Il metodo più utilizzato è il grafico di Brandt e Altman: se una delle due misure
rappresenta uno standard consolidato, va in ascissa, altrimenti ci si mette la
media delle due misure. In ordinata la corrispondente differenza tra le due
misure. Non è associato un test inferenziale.
Pagina 39
Misure di concordanza per dati
qualitativi
OSSERVATORE
B
OSSERVATORE
A
Efficienza
conservata
Mediamente
ridotta
Severamente
ridotta
Totale
Efficienza
conservata
225
3
12
240
Mediamente
ridotta
15
12
3
30
Severamente
ridotta
0
0
30
30
240
15
45
300
Totale
Il problema della concordanza si pone anche per valutazioni di tipo qualitativo.
Vediamo questo esempio immaginario. I numeri sono frequenze assolute.
Pagina 40
Misure di concordanza per dati
qualitativi
OSSERVATORE
B
OSSERVATORE
A
Efficienza
conservata
Efficienza
conservata
Mediamente
ridotta
Severamente
ridotta
225
Mediamente
ridotta
240
12
30
Severamente
ridotta
Totale
240
Concordanza osservata:
Totale
15
30
30
45
300
f0 = ∑i =1 fii = 225 + 12 + 30 = 267
k
Pagina 41
Misure di concordanza per dati
qualitativi
OSSERVATORE
B
OSSERVATORE
A
Efficienza
conservata
Efficienza
conservata
Mediamente
ridotta
Severamente
ridotta
225 (192)
Mediamente
ridotta
240
12 (1.5)
30
Severamente
ridotta
Totale
240
Concordanza dovuta al caso:
Totale
15
30 (4.5)
30
45
300
fe = ∑i =1 fi. ⋅ f.i = 192 + 1.5 + 4.5 = 198
k
La concordanza dovuta al caso è stimata dal valore atteso (come al solito, totale
di riga per totale di colonna divisio gran totale)
Pagina 42
Statistica k di Cohen
k=
fo − fe 267 − 198 69
=
=
= 0.676
N - fe 300 − 198 102
Concordanza completa:
k=1
Eccellente concordanza:
k>0.75
Scarsa concordanza:
k<0.40
Pagina 43
Statistica k di Cohen
k
se(k)
E’ distribuita come una deviata gaussiana standardizzata,
quando N>100
Pagina 44
Statistica k di Cohen
se(k) =
fe
198
198
=
=
= 0.08
N ⋅ (N − fe )
300 ⋅ (300 − 198)
30600
k
0.676
=
= 8.45
se(k) 0.08
ha distribuzione gaussiana
Pagina 45