Esercitazione

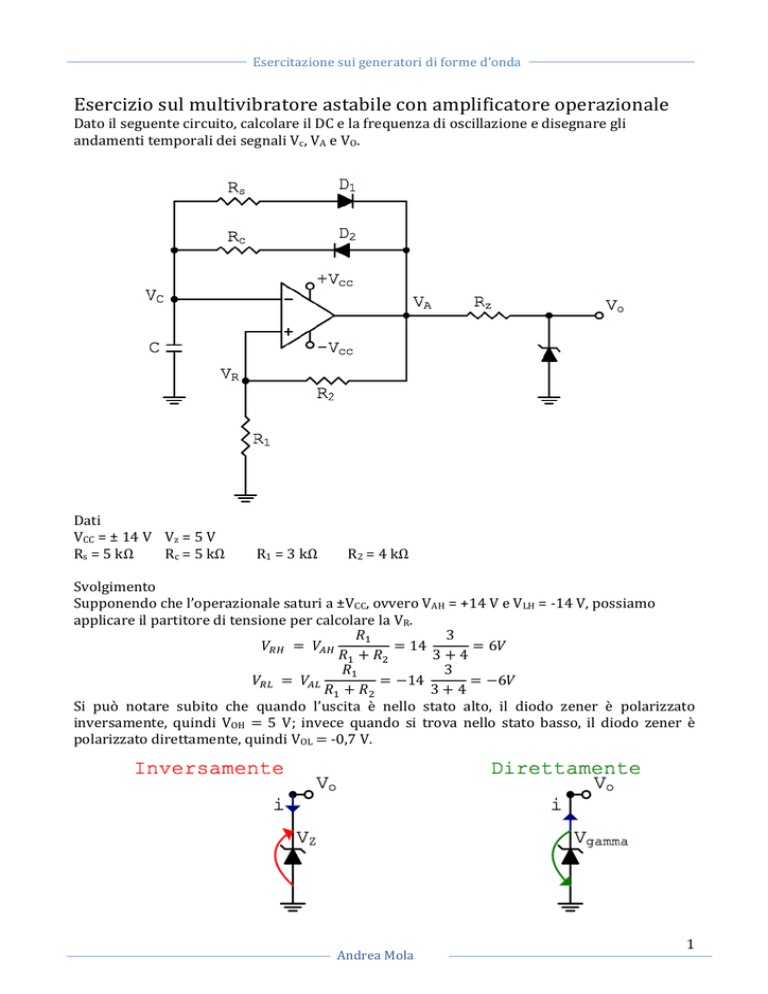
 Esercitazione sui generatori di forme d’onda Esercizio sul multivibratore astabile con amplificatore operazionale Dato il seguente circuito, calcolare il DC e la frequenza di oscillazione e disegnare gli andamenti temporali dei segnali Vc, VA e VO. Dati VCC = ± 14 V Vz = 5 V Rs = 5 kΩ Rc = 5 kΩ R1 = 3 kΩ R2 = 4 kΩ Svolgimento Supponendo che l’operazionale saturi a ±VCC, ovvero VAH = +14 V e VLH = -­‐14 V, possiamo applicare il partitore di tensione per calcolare la VR. 𝑅!
3
𝑉!" = 𝑉!"
= 14 = 6𝑉 𝑅! + 𝑅!
3+4
𝑅!
3
𝑉!" = 𝑉!"
= −14 = −6𝑉 𝑅! + 𝑅!
3+4
Si può notare subito che quando l’uscita è nello stato alto, il diodo zener è polarizzato inversamente, quindi VOH = 5 V; invece quando si trova nello stato basso, il diodo zener è polarizzato direttamente, quindi VOL = -­‐0,7 V. Andrea Mola 1 Esercitazione sui generatori di forme d’onda Analizziamo il funzionamento a partire dalla situazione con condensatore C scarico, ovvero VAL-­‐-­‐>VAH. Inizialmente avrò VC = VRL = -­‐6 V, in questo istante inizia la fase di carica del condensatore attraverso la sola resistenza RC, siccome nel ramo dove è presente RS c’è un diodo polarizzato inversamente che si comporta come un circuito aperto. Quindi, Viniziale = VRL = -­‐6 V ed il condensatore vorrebbe tendere al potenziale in uscita dall’amplificatore operazionale, ovvero Vfinale = VAH – 0,7 V = 13,3 V, ma logicamente (per la proprietà degli amplificatori operazionali) il valore massimo che potrà raggiungere sarà uguale al potenziale sul morsetto positivo, ovvero VC(TA) = VRH = 6 V. Il tempo di carica del condensatore è determinato da τC = RC C = 2 ms. Ora ci rimane solo da calcolare il TA: 𝑉!"#$%& − 𝑉!"!#!$%&
𝑇! = 𝜏! ln
= 1,94 𝑚𝑠 𝑉!"#$%& − 𝑉! (𝑇! )
Ora il condensatore C è carico, ossia VC = VRH = 6 V e iniziamo il processo di scarica VAH-­‐-­‐>VAL. In questo caso sarà il diodo D2 a comportarsi come un circuito aperto, quindi il nostro condensatore C si scarica solo sulla resistenza RS, con un tempo pari a τS = RS C = 2 ms. Quindi, Andrea Mola 2 Esercitazione sui generatori di forme d’onda Viniziale = VRH = 6 V ed il condensatore vorrebbe tendere al Vfinale = VAL – (-­‐0,7 V) = -­‐13,3 V, ma come prima il valore massimo che potrà raggiungere sarà VC(TB) = VRL = -­‐6 V. Ora ci rimane solo da calcolare il TB: 𝑉!"#$%& − 𝑉!"!#!$%&
𝑇! = 𝜏! ln
= 0,49 𝑚𝑠 𝑉!"#$%& − 𝑉! (𝑇! )
Dopo esserci calcolati i tempi in cui il segnale d’uscita VO rimangono alti e bassi, possiamo calcolarci il periodo totale dell’onda T = TA + TB = 2,43 ms Il cui duty cicle è: 𝑇!
𝐷𝐶 = 100 ≈ 80% 𝑇
con frequenza pari a 1
𝑓 = = 410 𝐻𝑧 𝑇
Andrea Mola 3 Esercitazione sui generatori di forme d’onda Esercizio sul multivibratore monostabile con amplificatore operazionale Dato il seguente circuito, dimensionare R2, R1, R e C e disegnare gli andamenti temporali dei segnali Vc, VA e VO. Dati VCC = ±10 V VR = ±3 V Vz = 5 V T = 5 ms Svolgimento Si può notare subito che quando l’uscita è nello stato alto, il diodo zener è polarizzato inversamente, quindi VOH = 5 V; invece quando si trova nello stato basso, il diodo zener è polarizzato direttamente, quindi VOL = -­‐0,7 V. Supponendo che l’operazionale saturi a ±VCC, ovvero VA = ±10 V, possiamo calcolare le resistenze R1 e R2 applicando il partitore di tensione e ribaltando la formula. 𝑅!
𝑉! 𝑅!
3
𝑉! = 𝑉!
⇒
= = 𝑅! + 𝑅!
𝑉!
𝑅! + 𝑅! 10
Fissando R1 (o R2), posso calcolare R2 (o R1), R1 = 3 KΩ e dai calcoli si ottiene R2 = 7 KΩ. Ora, come sappiamo la durata dell’impulso T è pari alla formula inversa della tensione Vc(T). 𝑉!"#$%& − 𝑉!"!#!$%&
𝑇 = 𝜏 ln
𝑉!"#$%& − 𝑉! (𝑇)
con τ che si riferisce al tempo di carica nel caso di multivibratore monostabile a livello basso ( tempo di scarica nel caso di livello alto), in questo caso la τ è uguale sia per la carica sia per la scarica. Andrea Mola 4 Esercitazione sui generatori di forme d’onda τ = RC Viniziale = -­‐0,7 V Vfinale = VAH = 10 V VC(T) = VRH = 3 V sempre fissando R (o C) posso trovare C (o R) 𝑇
5 𝑚
𝑅𝐶 =
=
= 11,78 𝑚𝑠 10 + 0,7
𝑉!" − (−0,7)
ln
ln 𝑉 − 𝑉
10 − 3
!"
!"
Posto C = 1µF, si ottiene R = 11,7 KΩ Esercizio sugli oscillatori Dato il seguente circuito, calcolare o la frequenza fO o R e C. Inizio riconoscendo i rispettivi blocchi A e H: Andrea Mola 5 Esercitazione sui generatori di forme d’onda Blocco A: Il primo amplificatore operazionale è in configurazione non invertente, quindi 1
𝑍!
1
𝑗𝜔𝐶
𝑉!! = 1 +
𝑉! = 1 +
𝑉! = 1 +
𝑉 𝑍!
𝑅
𝑗𝜔𝑅𝐶 !
Invece, il secondo amplificatore operazionali è in configurazione invertente, quindi 1
𝑍!
1
𝑗𝜔𝐶
𝑉! = −
𝑉!! = −
𝑉!! = −
𝑉 𝑍!
𝑅
𝑗𝜔𝑅𝐶 !!
mettendo a sistema le due equazioni, risulta 𝑍!
𝑍!
1
1
𝑉! = −
1+
𝑉! = −
1+
𝑉 𝑍!
𝑍!
𝑗𝜔𝑅𝐶
𝑗𝜔𝑅𝐶 !
Dove, 𝑉!
1
1
1
1 + 𝑗𝜔𝑅𝐶
𝐴 𝑗𝜔 =
= −
1+
= −
𝑉!
𝑗𝜔𝑅𝐶
𝑗𝜔𝑅𝐶
𝑗𝜔𝑅𝐶
𝑗𝜔𝑅𝐶
Blocco H: Per il calcolo del blocco H sfrutto la regola del partitore di tensione 1
1
𝑍!
1
𝑗𝜔𝐶
𝑗𝜔𝐶
𝑉! =
𝑉! =
𝑉! =
𝑉! =
𝑉! 1
1 + 𝑗𝜔𝑅𝐶
𝑍! + 𝑍!
1
+
𝑗𝜔𝑅𝐶
𝑗𝜔𝐶 + 𝑅
𝑗𝜔𝐶
Dove, 𝑉!
1
𝐻 𝑗𝜔 =
=
𝑉! 1 + 𝑗𝜔𝑅𝐶
Ora posso ricavarmi l’espressione del guadagno d’anello: 1
1 + 𝑗𝜔𝑅𝐶
1
1 !
1 !
𝐴𝐻 𝑗𝜔 = −
=−
=
𝑗𝜔𝑅𝐶
𝑗𝜔𝑅𝐶
1 + 𝑗𝜔𝑅𝐶
𝑗𝜔𝑅𝐶
𝜔𝑅𝐶
Calcolo il modulo, essendo composto da sola parte reale coincide con l’espressione stessa 𝐴𝐻 𝑗𝜔 = 𝐴𝐻(𝑗𝜔) Andrea Mola 6 Esercitazione sui generatori di forme d’onda Calcolo la fase ∡!" = 𝑎𝑟𝑐𝑡𝑔
0
1
𝜔 ! 𝑅! 𝐶 !
= 𝑎𝑟𝑐𝑡𝑔 0 = 0 Dopo aver calcolato modulo e fase posso applicare le condizioni di Barkhausen, noto subito che la fase è già 0 quindi è sempre verificata, mi rimane solo da applicare la prima condizione. 1
|𝐴𝐻 𝑗𝜔 | = ! ! ! = 1 𝜔 𝑅 𝐶
1
𝜔=
𝑅𝐶
Andrea Mola 7