Moti piani (moti in due dimensioni)
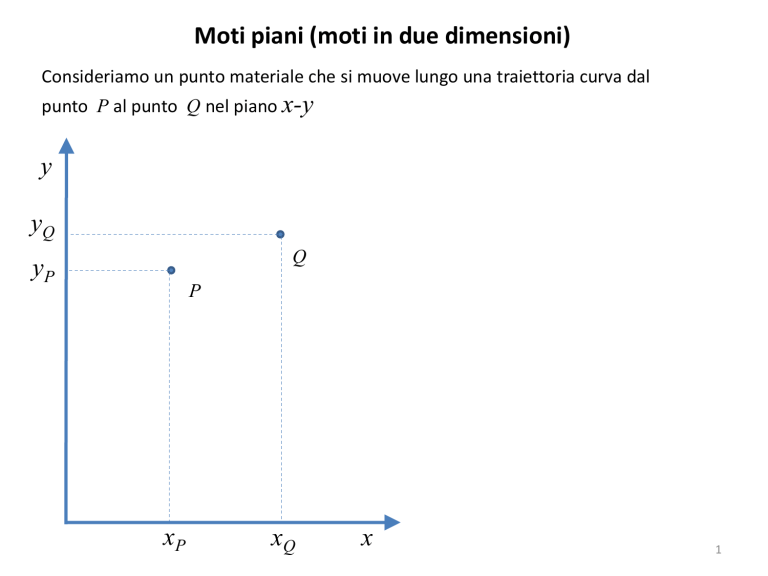
Consideriamo un punto materiale che si muove lungo una traiettoria curva dal
punto P al punto Q nel piano x-y
y
yQ
Q
yP
P
xP
xQ
x
1
Consideriamo un punto materiale che si muove lungo una traiettoria curva dal
punto P al punto Q nel piano x-y
y
yQ
Q
yP
P
xP
xQ
x
2
La posizione iniziale del punto materiale è individuata dal vettore
s così definito:
s = x + y = xP i + yP j
y
yQ
Q
y
P
s
x
xQ
x
3
La posizione finale del punto materiale è individuata dal vettore risultante dalla somma
vettoriale
s + Δs
Pertanto la velocità media del nostro punto
materiale durante sarà Δt :
y
v
yQ
Δs
y
=
Δs / Δt
e la direzione e il verso di questo vettore
Q
saranno quelli del vettore Δs
P
Applicando il solito processo al limite come
abbiamo fatto ne caso unidimensionale:
s + Δs
v = lim ( Δs/Δt ) = ds/dt
Si, ma in pratica come si calcola
la derivata di un vettore ?
x
xQ
x
4
E’ facile rendersi conto che mentre il punto materiale si muove lungo la traiettoria curva,
e cioè mentre il vettore s cambia direzione e modulo, le sue proiezioni sugli assi x e y
si muovono di moto rettilineo (ma non necessariamente uniforme).
Le velocità delle proiezioni, e cioè i vettori vx e vy
altro non sono che le componenti ortogonali del
y
vettore velocità v
yQ
Q
yP
vx = dx/dt
P
vy = dy/dt
E così siamo in grado di calcolare la derivata del
vettore velocità:
v = vx + vy
xP
xQ
x
5
Quando un punto materiale si muove lungo una linea retta, il suo vettore velocità
può avere qualsiasi modulo, ma è sempre diretto lungo la retta. Al contrario, quando
un punto materiale si muove in un piano, il vettore velocità può avere anche qualsiasi
direzione. E poiché la velocità lungo la curva è a somma vettoriale delle velocità
componenti lungo gli assi x e y, il vettore velocità risulta sempre tangente alla curva in
ciascun punto del moto.
y
vy
v
vx
x
6
In modo del tutto analogo possiamo scomporre il vettore accelerazione nelle
sue componenti x e y e in sostanza l’accelerazione di un punto materiale
che si muove in un piano lungo una traiettoria curva si ricava come somma
vettoriale delle accelerazioni componenti.
a = ax + ay
y
v
ay
a = dvx/dt + dvy/dt
a
ax
x
7
Quindi in sostanza, le stesse equazioni del moto che abbiamo applicato al caso
unidimensionale (riducibile in sostanza ad una trattazione scalare) sono applicabili al caso
bidimensionale (trattazione vettoriale), applicandole alle componenti del vettore.
Un caso interessante che possiamo trattare subito quindi è il caso di un moto in un piano
con accelerazione costante, di cui abbiamo già trattato il caso unidimensionale.
Avevamo visto che nel caso unidimensionale l’equazione del moto per a = costante era:
x(t) = x0 + v0 t + ½ at2
Dovendo essere ax e
a y, costanti (il vettore a si mantiene immutato nel tempo)
avremo per le due componenti del moto x e y :
x(t) = x0 + v0x t + ½ ax t2
y(t) = y0 + v0y t + ½ ay t2
s(t) = s0 + v0 t + ½ a t2
8
Moto di un proiettile
E questa infallibile equazione purtroppo è quella che viene utilizzata nei bombardamenti!
9
Moto circolare uniforme
Consideriamo adesso il caso di un punto che si muove di moto circolare uniforme:
Intendiamo il moto lungo una circonferenza di raggio r con velocità costante in modulo.
E’ ovvio che, sebbene il vettore velocità
v sia costante in modulo, esso cambia con
continuità in direzione. Esiste quindi un vettore accelerazione a che vogliamo calcolare
10
Piazziamo la nostra orbita circolare all’origine di un sistema di assi cartesiani , consideriamo
due istanti t1 e t2 in cui il punto si trova in posizioni simmetriche rispetto all’asse
definiamo con θ l’angolo fra i due vettori posizione agli istanti t1 e t2
y,e
Poiché ad ogni istante il vettore velocità è tangente alla circonferenza, e cioè risulta
ortogonale al raggio, risulta che l’angolo fra i due vettori v1 e
v2
θ
v1
y
θ
v2
v1
v2
Risulta quindi che questi due triangoli sono simili
(triangoli isosceli con lo stesso angolo al vertice)
Δv
Corda
x
r
θ
r
θ
v2
θ
v1
r
è=
11
Δv
Corda
r
θ
r
θ
v
v
Trattandosi di triangoli simili, i lati corrispondenti saranno proporzionali:
Corda / r
= Δv / v
Considerando un processo al limite in cui
θ
«Corda»
0
si ha:
v dt
Da cui risulta:
Δv / v = v Δt / r
Δv / Δt = v2 / r
a = lim (Δv / Δt)
Accelerazione centripeta:
= v2 / r
a = v2 / r
12
Sistemi di riferimento inerziali e moti relativi
Abbiamo introdotto varie grandezze fisiche fondamentali, la posizione di un punto
materiale, la sua velocità, l’accelerazione, abbiamo introdotto anche il formalismo
vettoriale, etc… e lo abbiamo fatto utilizzando liberamente un sistema di riferimento,
cioè un sistema di coordinate, tipicamente un sistema di assi cartesiani X-Y.
Adesso vale la pena di approfondire un po’ questa questione dei sistemi di riferimento.
Supponiamo di essere a bordo di un treno che si muove con velocità costante v lungo un
tratto rettilineo: il treno cioè si muove di moto rettilineo uniforme. Come in figura:
Velocità v = costante
13
Siamo seduti e abbiamo in mano una palla
da tennis. Vorremmo lanciarla al nostro vicino
di posto, imprimendole quindi una velocità
ortogonale a quella del treno.
v = 200 km/h
Cioè vorremmo fare una cosa così
14
Ma siamo sicuri che mentre la palla si muove
da sinistra verso destra, il treno che si muove
ad alta velocità non le «scappa sotto»
v = 200 km/h
E magari succede una cosa cosi ?
COSA NE PENSATE ?
15
Si osserva che se il treno è in moto rettilineo uniforme, e cioè NON è soggetto
ad alcuna accelerazione, non c’è nessun esperimento che possiamo fare a bordo
che ci dia informazioni sulla velocità del treno.
E infatti, l’unica informazione che abbiamo sul fatto che il treno è in moto, ci viene
dal panorama che osserviamo dai finestrini. Se li chiudiamo, noi a tutti gli effetti
NON possiamo affermare se il treno è fermo o è in moto.
Tutti gli esperimenti che faremo a bordo del treno, e che riferiremo rispetto ad
un sistema di riferimento ad esso solidale, daranno gli stessi risultati, sia che il treno
sia fermo che se è in moto rettilineo uniforme.
Un sistema di riferimento del genere si chiama
Sistema Inerziale
16
Un osservatore a bordo del treno osserverà che:
La pallina da tennis si muove lungo la direzione trasversale di moto accelerato
mentre possiede velocità zero lungo la direzione longitudinale del treno
Allo stesso tempo, un osservatore a terra fuori dal treno che ne osserva il moto
longitudinale, misurerà invece una velocità della pallina da tennis pari a quella del treno
In sostanza: i due osservatori NON concordano sulla velocità longitudinale della pallina
17
E riguardo al moto trasversale della pallina, quello che da
dentro risulta accelerato, cosa si osserverà da fuori ?
Si osserva esattamente lo stesso moto accelerato !
Quindi: due osservatori situati in due sistemi inerziali,
concordano sulla misura delle accelerazioni ma NON sulla
misura delle velocità.
18
Cinematica in una o più dimensioni:
riassunto generale
19
Abbiamo iniziato definendo le grandezze fisiche
fondamentali per trattare il moto in una dimensione:
Posizione
Spostamento: cambiamento di posizione
Velocità: rapidità con cui cambia la posizione
Accelerazione: rapidità con cui cambia la velocità
20
Abbiamo visto che si tratta di grandezze vettoriali, anche se nel caso di moto in
una dimensione possiamo trattare il problema adottando il formalismo scalare.
Abbiamo preso dimestichezza con il problema della risoluzione temporale di un
dato fenomeno fisico:
Per esempio: poiché lo spostamento è definito some la variazione di posizione
in un dato intervallo di tempo, la variazione di posizione durante l’intervallo Δt
di un punto materiale che si muove di un moto «bizzarro» può non essere esaustiva.
O
Δr
Δt
x
Tempo t
21
Ci siamo resi conto che «campionando» il nostro fenomeno fisico (in questo
caso il moto rettilineo di un punto materiale) con un intervallo di tempo relativamente
lungo, perdiamo dettagli che potrebbero essere importanti.
E infatti, applicando a questo caso la definizione di velocità, abbiamo stabilito che
la formula:
v = Δr / Δt
deve essere intesa come velocità media, grandezza fisica a volte utile, ma a volte
meno utile. Per esempio nel caso seguente:
O
Δr = 0
x
Risulterebbe:
v = Δr / Δt = 0
Δt
Tempo t
22
Ci siamo quindi resi conto della opportunità di campionare il fenomeno con una maggiore
risoluzione temporale, cioè con intervallo di tempo Δt sempre più piccoli, fino a pervenire a
una rappresentazione grafica «continua» della posizione x(t) in funzione del tempo:
x
x
Δt→0
Tempo t
Tempo t
23
Per ogni istante t abbiamo definito la velocità istantanea v(t) come il valor limite a cui
tende il rapporto Δr / Δt quando Δt tende a zero:
v = lim ( Δr/Δt ) m / s
Δt→0
x=vt
x
x
Δt→0
Tempo t
In ogni punto, la velocità
istantanea v(t) è il
coefficiente angolare della
retta tangente la curva x(t)
Tempo t
24
Essendo in grado di ricavare una serie «fitta» di punti per la velocità istantanea
v(t),
siamo stati in grado di farne una interpolazione grafica, e ci siamo resi conto che a questo
punto eravamo in grado di applicare le stesso processo a limite (Δt 0) per ricavare
l’accelerazione istantanea, che in ogni punto è il coefficiente angolare della retta tangente
alla funzione velocità v(t) così come la velocità istantanea era il coefficiente angolare
della retta tangente alla funzione spostamento x(t).
A questo proposito abbiamo visto un esempio abbastanza semplice: una particella che
parte da un punto P localizzato a 1m dall’origine e si sposta verso il punto Q localizzato a 5
m dall’origine e quindi torna indietro al punto R a 2 m dall’origine.
0
P
R
1
2
Q
3
4
5
6
7
8
9
x
25
6 m
Abbiamo definito un sistema di assi cartesiani per x e t.
Lo spostamento in questo sistema di assi sarà descritto da una curva così.
x
3
4
5
Q
1
2
R
P
t
1
2
3
4
sec
Abbiamo calcolato la velocità istantanea
elevato di punti
vi (ti) in numero di
punti sufficientemente
x
Q
R
P
t
1
2
3
4
sec
4 m/s
A questo punto abbiamo definito un sistema di assi cartesiani per vx e t, e abbiamo
Riportato i valori delle velocità istantanee calcolate nei vari punti e abbiamo operato
una interpolazione grafica
vx
P
S
Q
-4
0
W
R
-8
t
1
2
3
4
sec
vx
-4
0
4 m/s
La linea curva che abbiamo individuato nel piano (vx , t) altro non è che la rappresentazione
grafica della velocita del punto materiale in funzione del tempo vx (t).
-8
t
1
2
3
4
sec
Di questa funzione vx(t) potremo calcolare l’accelerazione istantanea punto
= dv /dt
è la pendenza della retta tangente in ogni punto
vx
-4
0
4 m/s
ricordando che a
-8
t
1
2
3
4
sec
Abbiamo anche visto che nel caso unidimensionale, l’equazione del moto di un punto
materiale che si muove a partire da un punto inziale x0, con una velocità iniziale pari
a v0 e con una accelerazione a costante è la seguente:
x(t) = x0 + v0 t + ½ at2
E abbiamo visto alcuni esempi in cui a = g = −9,8 m/s2
31
Poi siamo passati dal caso unidimensionale al caso bidimensionale (moto in un piano)
e ci siamo resi conto che in questo caso l’uso del formalismo vettoriale non è opzionale
ma risulta obbligatorio. Questo in quanto non esiste una direzione unica, e la direzione
del moto va quindi definita dalle stesse grandezze in gioco. Infatti, in un piano
x-y ,
un punto materiale può manifestare il suo moto in una qualunque direzione.
In particolare, un punto che si muova lungo una linea curva, cambia continuamente direzione.
Tuttavia, ci siamo resi conto che il moto delle proiezioni del punto lungo le componenti
x-y è ovviamente
sempre un moto unidimensionale.
32
Mentre il punto materiale si muove lungo la traiettoria curva, le sue proiezioni sugli assi x e y
si muovono di moto rettilineo (ma non necessariamente uniforme).
y
Quindi: tutto ciò che abbiamo imparato sulle
yQ
Q
yP
equazioni del moto in una dimensione può essere
tranquillamente applicato alle componenti lungo
P
gli assi x e y delle varie grandezze fisiche:
xP
xQ
x
y
vx
vy
ax
ay
x
33
Poi, a proposito di moti in un piano (x-y) abbiamo definito un particolare moto,
il cosiddetto moto circolare uniforme. Abbiamo detto che per moto circolare uniforme
intendiamo il moto lungo una circonferenza di raggio r con velocità costante in modulo
E abbiamo scoperto che l’accelerazione che provoca il continuo cambiamento di velocità
(non in modulo ma in direzione e verso) è costante in modulo, è sempre diretta verso
il centro della circonferenza, e vale:
a = v2 / r
(accelerazione centripeta)
34












