Selezione stabilizzatrice per alcune
mutazioni cromosomiche
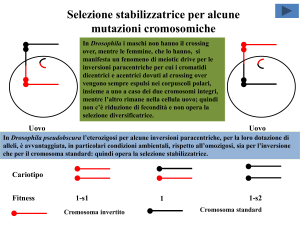
In Drosophila i maschi non hanno il crossing
over, mentre le femmine, che lo hanno, si
manifesta un fenomeno di meiotic drive per le
inversioni paracentriche per cui i cromatidi
dicentrici e acentrici dovuti al crossing over
vengono sempre espulsi nei corpuscoli polari,
insieme a uno a caso dei due cromosomi integri,
mentre l’altro rimane nella cellula uovo; quindi
non c’è riduzione di fecondità e non opera la
selezione diversificatrice.
Uovo
Uovo
In Drosophila pseudobscura l’eterozigosi per alcune inversioni paracentriche, per la loro dotazione di
alleli, è avvantaggiata, in particolari condizioni ambientali, rispetto all’omozigosi, sia per l’inversione
che per il cromosoma standard: quindi opera la selezione stabilizzatrice.
Cariotipo
Fitness
1-s1
Cromosoma invertito
1
1-s2
Cromosoma standard
Il meiotic drive attenua gli effetti negativi della
selezione diversificatrice subito dopo la comparsa
di mutazioni cromosomiche sottodominanti
Il meiotic drive a favore del cromosoma mutato, per cui i cromatidi del cromosoma standard
vengono in prevalenza espulsi nei corpuscoli polari, insieme a un cromatidio del cromosoma
mutato, mentre l’altro cromatidio del cromosoma mutato rimane nella cellula uovo, determina
un abbassamento del valore di equilibrio instabile p^=0,5 che può raggiungere lo 0 e una
conseguente riduzione in valore assoluto del Dp negativo e un aumento di quello positivo.
p=0
p=1
Dp=0
p=0,5
Uovo
Cromosoma mutato
Cromosoma standard
Il vantaggio per l’omozigote attenua gli effetti
negativi della selezione diversificatrice subito dopo la
comparsa di mutazioni cromosomiche sottodominanti
Il vantaggio selettivo del cromosoma mutato in omozigosi rispetto al cromosoma standard in
omozigosi, determina un abbassamento del valore di equilibrio instabile p^=0,5 e una
conseguente riduzione in valore assoluto del Dp negativo e un aumento di quello positivo.
p=0
p=1
Dp=0
p=0,5
s1>s2
Cariotipo
Fitness
1
Cromosoma mutato
1-s1
1-s2
Cromosoma standard
La deriva genetica
Quando una popolazione è molto grande (oltre le migliaia di individui) può essere
assimilata a una popolazione infinitamente grande: in assenza di altri fattori, le
frequenze degli alleli rimangono costanti con il passare delle generazioni
Più piccola è una popolazione, più è probabile che, per caso, le frequenze degli alleli
cambino ad ogni generazione: questo fenomeno è chiamato deriva genetica
Le probabilità delle frequenze alleliche alla generazione successiva hanno una
distribuzione binomiale (coefficienti delle potenze di un binomio); la variazione della
frequenza allelica tra 2 generazioni può essere sia un aumento che una diminuzione; le
variazioni piccole, in valore assoluto, sono più probabili di quelle grandi
La deriva genetica porta alla
fissazione di un allele e
all’eliminazione degli altri; più
piccola è la popolazione, più rapido
è il processo
Un allele neutrale appena sorto per
mutazione in una popolazione di N
individui ha una frequenza iniziale 1/2N,
una probabilità 1/2N di essere fissato e
(2N-1)/2N di essere eliminato
Esempi di cambiamenti casuali delle frequenze alleliche per deriva genetica a
partire da p=0,5 fino alla fissazione o all’eliminazione dell’allele azzurro scuro
probabilità di variazione delle frequenze alleliche da una
generazione all’altra per deriva genetica
La probabilità che un allele con frequenza pi nella generazione i in una popolazione di
n/2 individui diploidi assuma alla generazione i+1 la frequenza pi+1 = k/n è la seguente:
n
k
pik(1-p)n-k
in cui
n
=
n!/k!(n-k)!
k
In una popolazione di 3 individui bisessuati- uno A1A1, uno A1A2 e uno A2A2 –
p=q=0,5=1/2 se si estraggono casualmente i gameti che portano gli alleli A1 e A2, si
avranno nella generazione successiva, sempre di 3 individui, le seguenti frequenze
alleliche p di A1con le seguenti probabilità:
p=1/6
p=1/3
p=1/2
p=2/3
p=5/6
p=1
p=0
frequenza
probabilità
1/64
6/64
15/64
20/64
15/64
6/64
1/64
Mentre il valore di Dp è, per ogni valore di pi, univocamente determinato per segno e per
valore, se agiscono come fattori evolutivi la selezione, la mutazione o la migrazione, c’è una
distribuzione stocastica di valori, sia in aumento che in diminuzione, se il fattore evolutivo è
la deriva genetica.
La deriva genetica può portare alla
fissazione di alleli neutrali comparsi per
mutazione.
In una popolazione di 3 individui bisessuati (N=3), ciascuno con 2
“serbatoi” di gameti (n=2N=6), quando nella generazione i compare un
allele mutato neutrale (giallo) è sempre in eterozigosi e la sua frequenza è
p=1/2N=1/6, mentre l’altro allele (verde) ha frequenza q=(2N-1)/2N=5/6.
La probabilità generica
che nella generazione i+1
p=k/n è la seguente:
La probabilità che nella
generazione i+1
p=q=3/6=0,5 è la seguente:
n
k
6
3
(1/6)k(5/6)n-k
(1/6)3(5/6)3
= 0,05
Integrando tutte le possibili sequenze di generazioni che, attraverso la
prevalenza di incrementi del valore di p con il passare delle generazioni,
porta alla fissazione del nuovo allele (p=1), la probabilità complessiva della
sua fissazione è pari a1/6.
La deriva genetica può portare alla
fissazione di mutazioni cromosomiche
sottodominanti comparse per mutazione.
In una popolazione della stessa numerosità (N=3, n=2N=6),
quando nella generazione i compare una mutazione cromosomica
sottodominante (rosso) la sua frequenza è p=1/2N=1/6, mentre il
cromosoma standard (blu) ha frequenza q=(2N-1)/2N=5/6.
La mutazione compare sempre in eterozigosi; la
riduzione di fecondità negli eterozigoti, produce una
diminuzion nel numero dei gameti: nel modello
presentato si perde la metà dei gameti (s=0,5).
La probabilità generica
che nella generazione i+1
p=k/n è la seguente:
n
k
(1/10)k(9/10)n-k
La probabilità che nella generazione i+1
p=q=3/6=0,5 – cioè il valore al di sopra del quale
la mutazione cromosomica sottodominante
diviene avvantaggiata - è la seguente:
6
3
(1/10)3(9/10)3 = 0,015
Anche se non è possibile una stima analitica della probabilità di fissazione di
una mutazione cromosomica sottodominante dopo la sua comparsa per
mutazione, tale probabilità, pur più piccola rispetto a quella relativa ad alleli
neutrali, non è irrisoria per popolazioni molto piccole e/o bassi valori di s.
Sintesi sugli effetti dei fattori evolutivi
Mutazione
Migrazione
Deriva genetica
Selezione diversificatrice
Selezione stabilizzatrice
Selezione direzionale svantaggiosa
Selezione direzionale vantaggiosa
0
1
p
Fattore evolutivo
Selezione direzionale vantaggiosa
Selezione direzionale svantaggiosa
Selezione stabilizzatrice
Selezione diversificatrice
Deriva genetica
Migrazione
Mutazione
Valore di equilibrio stabile per p verso cui la
selezione stabilizzatrice fa convergere p
Valore di equilibrio instabile per p da cui la
selezione diversificatrice fa divergere p
Effetto sulla variabilità Effetto sulla variabilità
entro le popolazioni
tra le popolazioni
+
+
+
+
+
-
L’inincrocio preferenziale
L’inincrocio preferenziale è una delle modalità di incrocio diverse dalla panmissia
Se, in una popolazione con 2 alleli (A1 e A2) per il gene A, si incrociano tra loro gli
individui con lo stesso genotipo (omozigoti A1A1 fra loro, omozigoti A2A2 fra
loro, eterozigoti A1A2 fra loro, ad ogni generazione si riduce la frequenza degli
eterozigoti.
A1A1
A2A2
Generazione i
Generazione i+1
A1A2
Generazione i+2
Le frequenze degli omzigoti (f(A1A1) ed f(A2A2) sono più alte di quelle attese in base
alla 2° legge di Hardy Weinberg, quella degli eterozigoti (f(A1A2)) è più bassa; questo
allontanamento dall’equilibrio procede sempre di più con il passare delle generazioni.
f(A1A1)>p2; f(A2A2)>q2; f(A1A2)<2pq
Nel caso illustrato (p=q=0,5; autofecondazione), alla generazione i+n
f(A1A1)=f(A2A2)=(1-1 /2n)/2; f(A1A2)=1/2n
Per calcolare p e q, anche in assenza di panmissia, ci si basa sulle frequenze
genotipiche reali: p=f(A1A1)+0,5f(A1A2); q=f(A2A2)+0,5f(A1A2)
L’inincrocio riduce gli effetti della selezione
diversificatrice dopo la comparsa di mutazioni
cromosomiche sottodominanti
A1A1
A2A2
A1A2
Popolazione panmittica
f(A1A1)=p2; f(A2A2)=q2;
p=0
p=1
Dp=0
p=0,5
Popolazione con inincrocio
f(A1A1)>p2; f(A2A2)>q2;
L’inincrocio produce una riduzione della
frequenza degli eterozigoti rispetto a una
popolazione panmittica; quindi si riduce la
frazione della popolazione che subisce una
selezione negativa; ne deriva una riduzione in
valore assoluto del Dp negativo e positivo.
Mutazioni cromosomiche
sottodominanti e migrazione
Cromosomi
omologhi
m = tasso di migrazione (costante)
mc = tasso critico di migrazione
Popolazioni molto grandi di grandezza confrontabile
Popolazione monomorfa per
il cromosoma mutato
Popolazione monomorfa per
il cromosoma standard
m< mc: le due popolazioni conservano
stabilmente ciascuna il proprio cromosoma
m> mc: le due popolazion, attraverso un
equilibrio instabile…
…divengono entrambe monomorfe per
il cromosoma standard……
…o per il cromosoma mutato……
Popolazioni molto grandi di grandezza molto diversa
m< mc: la popolazione piccola conserva
stabilmente il cromosoma mutato
m> mc: la popolazione piccola diviene
monomorfa per il cromosoma standard
mc = s/4 per popolazioni di pari grandezza
mc = s/(8+s) per popolazioni di grandezza diversa
Le mutazioni cromosomiche sottodominanti hanno
una distribuzione politipica in metapopolazioni
Deme monomorfo per il
cromosoma mutato
Deme monomorfo per il
cromosoma standard
Deme transitoriamente
polimorfo
Migrazione tra i
demi con m< mc
Migrazione tra i
demi con m> mc
Immigrazione
con m> mc
Come risultato delle fluttuazioni del tasso di migrazione, il numero dei demi monomorfi per il
cromosoma mutato può casualmente aumentare (espansione del cromosoma mutato) o diminuire