7-Cerenkov

Effetto Cherenkov - 1
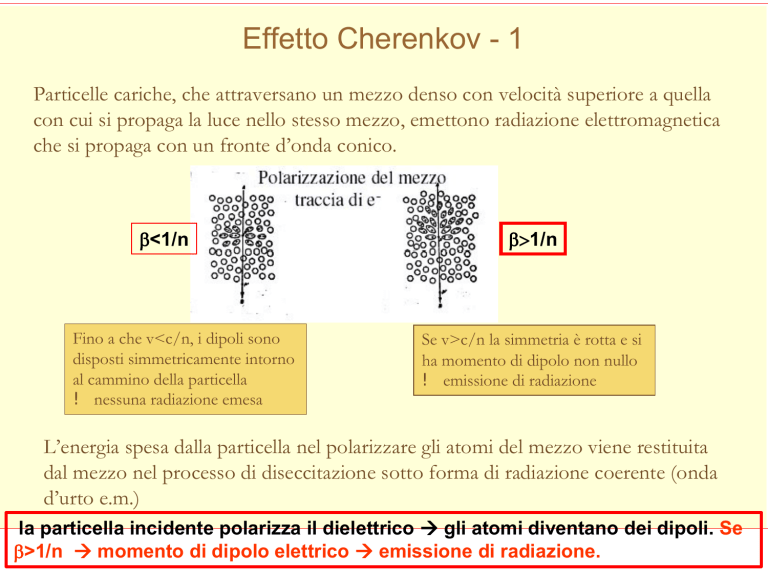
Particelle cariche, che attraversano un mezzo denso con velocità superiore a quella
con cui si propaga la luce nello stesso mezzo, emettono radiazione elettromagnetica
che si propaga con un fronte d’onda conico.
b<1/n
Fino a che v<c/n, i dipoli sono
disposti simmetricamente intorno
al cammino della particella
! nessuna radiazione emesa
b>1/n
Se v>c/n la simmetria è rotta e si
ha momento di dipolo non nullo
! emissione di radiazione
L’energia spesa dalla particella nel polarizzare gli atomi del mezzo viene restituita
dal mezzo nel processo di diseccitazione sotto forma di radiazione coerente (onda
d’urto e.m.)
la particella incidente polarizza il dielettrico  gli atomi diventano dei dipoli. Se
b>1/n
 momento di dipolo elettrico  emissione
di radiazione.
Fisica Nucleare e Subnucleare II, 2007-8
19
Lezioni 6 e 7 seconda parte
RICH: SuperKamiokande
M. Sozzi
Lab. Fisica Interaz. Fondamentali
Effetto Čerenkov (5)
Luce Cerenkov in reattore nucleare
Anelli Cerenkov a SuperKamiokande
M. Sozzi
Lab. Fisica Interaz. Fondamentali
Effetto Cherenkov - 5
Nel disegno di rivelatori di luce Cherenkov è opportuno calcolare il numero di
fotoni emessi per unità di cammino percorso (x [cm]) per una particella di carica
ze per unità di energia o di lunghezza d’onda:
d 2N
z 2# &
1 )
d 2 N 2 z 2#
=
=
(1
+ oppure
2 2
d² dx
c ¢ % n (² )
d, dx
,2
&
1 )
(1
+
2 2
¢ % n (, )
Trascurando la dispersione nel mezzo (considerando cioè n indipendente da ¢ )
ed integrando su un opportuno intervallo di lunghezza d'onda
¢
dN
1
2
= 2² z # )1
,
2 2
dx
( % n ( &) +
&2
&1
¢ 1
d&
2
2
= 2² z # sin . C )
2
&
( &1
Integrando nell'intervallo di ¢ tipico dei
fotomoltiplicatori bialcali (350< ¢ <550 nm)
otteniamo
1
,
&2 +
dN
= 475 z 2 sin 2 ² C fotoni/cm
dx
Il numero di fotoni prodotti dipende da n: n grande % pochi fotoni !
La luce Cerenkov e' prodotta massimamente per piccoli ¢ , nell’ UV.
Fisica Nucleare e Subnucleare II, 2007-8
!
Lezioni 6 e 7 seconda parte
23
Spettro di fotoni Cherenkov
per 300nm< ¢ < 650nm
Sensibilità (Quantum
efficiency) di un PMT bialcali
Contatori basati sull'effetto Cherenkov
I contatori basati sull'Effetto Cherenkov normalmente vengono utilizzati per misurare
la velocità ² delle particelle cariche (ad esempio negli esperimenti agli
acceleratori, su pallone atmosferico o nello spazio). Se dal rivelatore Cherenkov
otteniamo la velocità della particella (v= ² c) e da un'altra parte dell'apparato (ad
esempio dalla misura di deflessione in campo magnetico) ne otteniamo l'impulso
(p = m v) combinando le informazioni possiamo determinarne la massa m (e
quindi identificare il tipo di particella).
COMPONENTI PRINCIPALI:
1 Radiatore: mezzo che produce la luce all’ attraversamento di particelle cariche di
opportuna velocità di lunghezza L
2 Raccolta di luce
3 Fotorivelatore
Ricordiamo che l'effetto Cherenkov è a soglia: solo particelle con velocità superiore al
valore definito dall’ indice di rifrazione danno un segnale per emissione di luce
Cherenkov
Fisica Nucleare e Subnucleare II, 2007-8
Lezioni 6 e 7 seconda parte
25
Telescopi Air Cherenkov
Le particelle cariche generate in uno "Sciame Esteso nell'Atmosfera" generano fotoni Cerenkov
• Il numero dei fotoni visibili è proporzionale alla energia iniziale
• La luce di fondo del cielo notturno definisce l’energia di soglia di rivelazione. Le osservazioni
vanno eseguite durante le notti serene e senza luna.
•
Fisica Nucleare e Subnucleare II, 2007-8
Lezioni 6 e 7 seconda parte
28
THE SURFACE DETECTOR ARRAY
Surface Detector (SD): 1600 water Cherenkov
tanks, 100% duty cycle
GPS antenna
Electronics
FE, 40 MHz FADC
3 PMTs
Batteries
12 t of purified water
Comms antenna
Solar panel
Effetto Cherenkov in mare/ghiaccio per rivelare
neutrini astrofisici di altissima energia
Il telescopio consisterà di ~5000
rivelatori di fotoni posizionati a
grande profondità
Profondità: 3500m
neutrino
Distanza dalla costa: 80 km
AGN
neutrino
Picture from ANTARES
Schema di principio dei Telescopi Cherenkov per neutrini
In mare: NEMO-ANTARES
Al Polo Sud nel
ghiaccio:
AMANDA-ICECUBE
Fisica Nucleare e Subnucleare II, 2007-8
30
Riassunto lezione 5-8
Radiazione di transizione
La radiazione di transizione è emessa quando una particella carica attraversa un
mezzo con un indice di rifrazione discontinuo, e.g. alla superfice di separazione fra il
vuoto ed un dielettrico
.
medium
vacuum
Una visione semplicistica
electron
Rivelatori di Particelle
16
Radiazione di transizione
 L’energia irraggiata ad ogni superfice di separazione e’:
1
W   p
3
N ee2
p 
 0 me
solo e± di alta energia
emettono TR.
Identificatione of e±
W 
 plasma

 frequency
N ph 

  p  20eV (plastic radiators)

W
1
 

137
 Il numero di fotoni emessi per superfice di separazione e’ piccolo:
Rivelatori di Particelle
17
 I raggi X sono emessi a piccolo angolo:
 1

 Spettro di emissione della radiazione di transizione (TR):
1
   p
( p  frequenza di plasma )
4
 I radiatori devono essere a basso Z
Bisogna evitare di riassorbire I fotoni emessi (vedi in seguito effetto fotoelettrico
proporzionale a Z5).
 Lo spessore dei radiatori deve essere ≥ della lunghezza di
formazione D.
c
D
p
Rivelatori di Particelle
18
TRD
Transition Radiation Detector
ö
dE a æ w P21 + w P2 2 + 2w 2 / g 2
w 2 / g 2 + w P21
÷÷
= çç
log
2
2
2
2
2
2
dw p è
w P1 - w P 2
w / g + wP2
ø
E=
2agw P1
3
(w P 2 << w P1 )
Intrerfacce multiple
Rivelatore a gas pesante
(Xe) per rivelare fotoni X
M. Sozzi
Lab. Fisica Interaz. Fondamentali