Lezione 7
Effetto Cerenkov
Per una trattazione classica dell’effetto Cerenkov
consultare Jackson : Classical Electrodynamics cap 13
e paragrafi 13.4 e 13.5
Rivelatori di Particelle
1
Lezione 7
Effetto Cerenkov
La radiazione Cerenkov e’ emessa ogniqualvolta una particella carica
attraversa un mezzo (dielettrico) con velocita’ bc=v>c/n, dove v e’ la velocita’
della particella e n l’indice di rifrazione del mezzo.
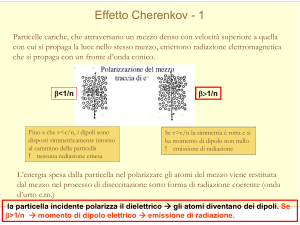
Intuitivamente: la particella incidente polarizza il dielettrico gli atomi
diventano dei dipoli. Se b>1/n momento di dipolo elettrico emissione di
radiazione.
b>1/n
b<1/n
Rivelatori di Particelle
2
Lezione 7
Effetto Cerenkov
L’ angolo di emissione qc puo’ essere interpretato qualitativamente come
un’onda d’urto come succede per una barca od un aereo supersonico.
llight=(c/n)t
wave
front
q
lpart=bct
1
cosq C
nb
with n n(l ) 1
qC
Esiste una velocita’ di soglia bs = 1/n qc ~ 0
Esiste un angolo massimo qmax= arcos(1/n)
La cos(q) =1/bn e’ valida solo per un radiatore infinito, e’ comunque una
buona approssimazione ogniqualvolta il radiatore e’ lungo L>>l essendo l la
lunghezza d’onda della luce emessa
Rivelatori di Particelle
3
Lezione 7
Effetto Cerenkov
Numero di fotoni emessi per unita’ di
lunghezza e intervallo unitario di
lunghezza d’onda. Osserviamo che
decresce al crescere della l
dN/dl
l
d 2 N 2z 2
1 2z 2 2
1
sin q C
2
2 2
2
dxdl
l b n
l
d 2N
1
2
dxdl l
c
hc
with l
E
d 2N
const.
dxdE
dN/dE
Il numero di fotoni emessi per unita’ di
Lunghezza non dipende dalla frequenza
Rivelatori di Particelle
4
Lezione 7
Effetto Cerenkov
dE
1
2
d
z 1 2 2
dx
c b n
L’ energia persa per radiazione Cerenkov cresce con b. Comunque
anche con b 1 è molto piccola.
Molto piu’ piccola di quella persa per collisione (Bethe Block), al
massimo 1% .
qmax (b=1)
air
1.000283 1.36
isobutane 1.00127 2.89
water
1.33
41.2
quartz
1.46
46.7
medium
n
Rivelatori di Particelle
Nph (eV-1 cm-1)
0.208
0.941
160.8
196.4
5
Lezione 7
Effetto Cerenkov
1)
Esiste una soglia per emissione di luce Cerenkov
2)
La luce e’ emessa ad un angolo particolare
Facile utilizzare l’effetto Cerenkov per identificare le particelle.
Con 1) posso sfruttare la soglia Cerenkov a soglia.
Con 2) misurare l’angolo DISC, RICH etc.
La luce emessa e rivelabile e’ poca.
Consideriamo un radiatore spesso 1 cm un angolo qc = 30o ed un E = 1 eV ed una particella di carica1.
N ph
dN
z 2
sin 2 c
dEdx c
370 sin 2 c L E 370 0.25 92.5
Considerando inoltre che l’efficienza quantica di un fotomoltiplicatore e’ ~20%
Npe=18 fluttuazioni alla Poisson
Rivelatori di Particelle
6
Lezione 7
Effetto Cerenkov
L’ indice di rifrazione dipende dalla frequenza n=n(E) e dn/dE≠ 0
→
errore cromatico
s c
1
1 dn
sn
sE
n tg
n tg dE
sE e’ connesso all’ intervallo E considerato.
dN/dE
Assumendo distribuzione piatta
sE= E/(12)1/2
L’ errore cromatico puo’ essere ridotto riducendo E e quindi il numero di
Fotoni emessi o con correzioni ottiche complicate
Rivelatori di Particelle
7
Lezione 7
Radiazione di transizione
Per una trattazione (qualitativa) della radiazione di
transizione consultare Jackson : Classical
Electrodynamics cap 14 paragrafo 9.
Un trattamento relativistico e’ esposto in: G.Garibian,
Sov. Phys. JETP63 (1958) 1079
Rivelatori di Particelle
8
Lezione 7
Radiazione di transizione
La radiazione di transizione e’ stata predetta da Ginzburg
e Franck nel 1946
La radiazione di transizione è emessa quando una particella carica
attraversa un mezzo con un indice di rifrazione discontinuo, e.g. alla
superfice di separazione fra il vuoto ed un dielettrico.
medium
vacuum
Una visione semplicistica
electron
Rivelatori di Particelle
9
Lezione 7
Radiazione di transizione
Si puo’ ricavare che:
L’energia irraggiata ad ogni superfice di separazione e’:
1
W p
3
solo e± di alta energia
emettono TR.
Identificatione of e±
W
plasma
p 20eV (plastic radiators)
frequency
Il numero di fotoni emessi per superfice di separazione e’ piccolo:
N ee2
p
0 me
N ph
W
1
137
Servono molte superfici di separazione molti fogli (plastica) separati da strati di gas (aria)
Rivelatori di Particelle
10
Lezione 7
Radiazione di transizione
Inoltre:
I raggi X sono emessi a piccolo angolo:
1
I raggi X sono vicini alla traccia della particella.
Spettro di emissione della radiazione di transizione (TR):
1
( p frequenza di plasma )
Energia tipica: p
4
• Simulated emission
spectrum of a CH2 foil
stack
Rivelatori di Particelle
11
Lezione 7
Radiazione di transizione
I radiatori devono essere a basso Z
Bisogna evitare di riassorbire I fotoni emessi (vedi in seguito effetto fotoelettrico
proporzionale a Z5).
Lo spessore dei radiatori deve essere ≥ della lunghezza di formazione D.
D
c
p
Per materiale tipo plastica p ~ 30x1015 s-1 e se ~ 1000
D ~ 10 mm.
Rivelatori di Particelle
12