Effetto Cherenkov

Effetto Cherenkov - 1
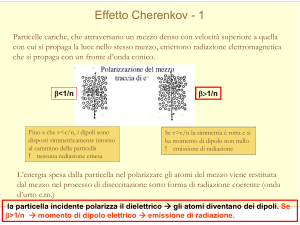
Particelle cariche, che attraversano un mezzo denso con velocità superiore a quella
con cui si propaga la luce nello stesso mezzo, emettono radiazione elettromagnetica
che si propaga con un fronte d’onda conico.
Fino a che v<c/n, i dipoli sono
disposti simmetricamente intorno
al cammino della particella
! nessuna radiazione emesa
Se v>c/n la simmetria è rotta e si
ha momento di dipolo non nullo
! emissione di radiazione
L’energia spesa dalla particella nel polarizzare gli atomi del mezzo viene restituita
dal mezzo nel processo di diseccitazione sotto forma di radiazione coerente (onda
d’urto e.m.)
Fisica Nucleare e Subnucleare II, 2007-8
Lezioni 6 e 7 seconda parte
19
Effetto Cherenkov - 2
La radiazione Cherenkov è emessa poiché la particella carica polarizza gli atomi
lungo la sua traccia così che essi diventano dipoli elettrici. La variazione nel tempo
della carica di dipolo porta all’emissione di radiazione EM
Prevista dalla teoria di Maxwell, l’esistenza di questa radiazione fu provata sperimentalmente
dal fisico russo Cherenkov nel 1934. Frank & Tamm calcolarono lo spettro della radiazione e
la relazione tra angolo di emissione e indice di rifrazione (Cherenkov, Frank e Tamm Premio Nobel 1958)
Mezzo dielettrico caratterizzato da:
Velocità della luce in un mezzo:
Velocità di una particella carica:
n = indice di rifrazione
c/n (c = velocità della luce nel vuoto)
V = "c
Il contributo della radiazione Cherenkov alla perdita di energia è piccolo
confrontato con quello dovuto a ionizzazione e eccitazione (~1/1000)
Fisica Nucleare e Subnucleare II, 2007-8
Lezioni 6 e 7 seconda parte
20
Effetto Cherenkov - 3
L’angolo tra i fotoni Cherenkov emesi e la traccia della particella carica
può essere calcolato con semplici considerazioni geometriche:
C
on
t
o
f
e
$C
A
particella
AB = t " c
percorso del µ nel tempo t
AC = t c/n
propagazione del fotone
prodotto in A per t=0
B
AC = AB cos $C
% cos $C=(1/"n) ! 1 % " " 1/n
Considerando particelle con "=1
nell'atmosfera
n~1.00029
In acqua di mare n~1.335
$~ 1.3o
$~ 42o
Molto meno fotoni (~ 200 – 250 #/cm ) che nel caso di scintillazione ~ 1/100
Fisica Nucleare e Subnucleare II, 2007-8
Lezioni 6 e 7 seconda parte
21
Effetto Cherenkov - 4
Si ha emissione di radiazione Cherenkov solo se
" >1/n
Effetto a soglia
cos $Cth = 1/"th n = 1
$Cth = 0
Soglie di rivelazione in acqua (n=1.335)
e± 0.768 MeV
µ± 158.7 MeV
&± 209.7 MeV
L’angolo Cherenkov cresce fino a raggiungere un massimo per "=1
Fisica Nucleare e Subnucleare II, 2007-8
Lezioni 6 e 7 seconda parte
22
Effetto Cherenkov - 5
Nel disegno di rivelatori di luce Cherenkov è opportuno calcolare il numero di
fotoni emessi per unità di cammino percorso (x [cm]) per una particella di carica
ze per unità di energia o di lunghezza d’onda:
d 2N
z 2# &
1 )
d 2 N 2-z 2# &
1 )
=
=
(1$ 2 2
+ oppure
(1$ 2 2 +
2
d"dx
c ' % n (" ) *
d,dx
, ' % n ( ,) *
Trascurando la dispersione nel mezzo (considerando cioè n indipendente da ')
ed integrando su un opportuno intervallo di lunghezza d'onda
'1 1*
'
dN
1 * &2 d&
2
2
2
= 2" z #)1$ 2 2 , - & 2 = 2" z # sin .C ) $ ,
dx
( % n ( &) + 1 &
( &1 &2 +
!
!
Integrando nell'intervallo di ' tipico dei
fotomoltiplicatori bialcali (350< '<550 nm)
otteniamo
dN
= 475 z 2 sin 2 "C fotoni/cm
dx
Il numero di fotoni prodotti dipende da n: n grande % pochi fotoni !
La luce Cerenkov e' prodotta massimamente per piccoli ', nell’ UV.
Fisica Nucleare e Subnucleare II, 2007-8
!
Lezioni 6 e 7 seconda parte
23
Spettro di fotoni Cherenkov
per 300nm< ' < 650nm
Fisica Nucleare e Subnucleare II, 2007-8
Sensibilità (Quantum
efficiency) di un PMT bialcali
Lezioni 6 e 7 seconda parte
24
Contatori basati sull'effetto Cherenkov
I contatori basati sull'Effetto Cherenkov normalmente vengono utilizzati per misurare
la velocità " delle particelle cariche (ad esempio negli esperimenti agli
acceleratori, su pallone atmosferico o nello spazio). Se dal rivelatore Cherenkov
otteniamo la velocità della particella (v= " c) e da un'altra parte dell'apparato (ad
esempio dalla misura di deflessione in campo magnetico) ne otteniamo l'impulso
(p = m v) combinando le informazioni possiamo determinarne la massa m (e
quindi identificare il tipo di particella).
COMPONENTI PRINCIPALI:
1 Radiatore: mezzo che produce la luce all’ attraversamento di particelle cariche di
opportuna velocità di lunghezza L
2 Raccolta di luce
3 Fotorivelatore
Ricordiamo che l'effetto Cherenkov è a soglia: solo particelle con velocità superiore al
valore definito dall’ indice di rifrazione danno un segnale per emissione di luce
Cherenkov
Fisica Nucleare e Subnucleare II, 2007-8
Lezioni 6 e 7 seconda parte
25
Contatori Cherenkov Differenziali
Ricordiamo che cos $C = 1/" n l'angolo di emissione della luce
dipende da " !!! Se la direzione della particella in esame è nota è
possibile selezionare particelle particelle di un determinato tipo:
realizzare cioè un contatore differenziale (selezionando sul momento
e/o sulla massa della particella). La geometria del rivelatore infatti può
definire un intervallo angolare preciso per accettare la luce Cherenkov
emessa
Fisica Nucleare e Subnucleare II, 2007-8
Lezioni 6 e 7 seconda parte
26
Produzione di luce Cherenkov in aria
A livello del mare l’indice di rifrazione dell’aria e’ n=1.00029.
Per una particella relativistica con "=0,9999 si ha produzione di luce Cherenkov, l’angolo di
propagazione della luce e’ dato da cos($Cherenkov) = 1/ (" n) ==> $Cherenkov ~23 mrad ~ 1.3°
La condizione di soglia per l’effetto Cherenkov (cos($Cherenkov) !1 ) comporta per elettroni e
muoni le condizioni:
elettroni Ee " 21 MeV
Energia di soglia per produzione di luce Cherenkov in aria <
muoni
Eµ " 4.4 GeV
Il massimo sviluppo dello sciame (quindi il massimo di produzione della luce Cherenkov) si ha
a ~ 10 km di altezza.
Cio’ implica che l’area illuminata al suolo ha forma circolare/ellittica (dipende dall’inclinazione
del RC primario) ed ha raggio~ 10000*0.023 = 230m.
La superficie illuminata ha quindi dimensione 1.6 * 105 m2. Parimenti possiamo dire che un
osservatore (uno strumento) al suolo puo’ ricevere luce da un punto qualsiasi di una superficie
di 1.6 * 105 m2 posta a 10 km di altezza.
Si puo’ calcolare facilmente il n. di fotoni Cherenkov emessi in funzione della lunghezza
d’onda. Per la radiazione “visibile” (350 < ' < 500 nm) ci aspettiamo, in uno sciame E.M.
iniziato da 1 fotone da 1 TeV, circa N# ~ 8.2·103 fotoni/', cio’ comporta al suolo un flusso di
fotoni pari a 30-50 fotoni/m2 in un’area compresa entro 100m dall’asse dello sciame.
Fisica Nucleare e Subnucleare II, 2007-8
Lezioni 6 e 7 seconda parte
27
Telescopi Air Cherenkov
Le particelle cariche generate in uno "Sciame Esteso nell'Atmosfera" generano fotoni Cerenkov
• Il numero dei fotoni visibili è proporzionale alla energia iniziale
• La luce di fondo del cielo notturno definisce l’energia di soglia di rivelazione. Le osservazioni
vanno eseguite durante le notti serene e senza luna.
•
Fisica Nucleare e Subnucleare II, 2007-8
Lezioni 6 e 7 seconda parte
28
Effetto Cherenkov in mare/ghiaccio per rivelare
neutrini astrofisici di altissima energia
Il telescopio consisterà di ~5000
rivelatori di fotoni posizionati a
grande profondità
Profondità: 3500m
neutrino
Distanza dalla costa: 80 km
AGN
neutrino
Fisica Nucleare e Subnucleare II, 2007-8
Lezioni 6 e 7 seconda parte
Picture from ANTARES
29
Schema di principio dei Telescopi Cherenkov per neutrini
In mare: NEMO-ANTARES
Al Polo Sud nel
ghiaccio:
AMANDA-ICECUBE
Fisica Nucleare e Subnucleare II, 2007-8
Lezioni 6 e 7 seconda parte
30