proc corr

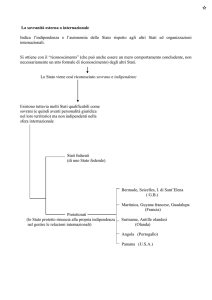
Test Statistici
Metodi Quantitativi per Economia,
Finanza e Management
Esercitazione n°5
Lavoro di gruppo
• Attendere la validazione del questionario e procedere
alla somministrazione dello stesso
• Argomenti da trattare nel lavoro di gruppo:
– Analisi univariata
– Analisi bivariata
– Test statistici
– Analisi fattoriale
– Regressione lineare utilizzando come regressori i
fattori
Test per lo studio dell’associazione
tra variabili
• Nella teoria dei test, il ricercatore fornisce ipotesi riguardo la
distribuzione
della
popolazione;
tali
ipotesi
sono
parametriche se riguardano il valore di uno o più parametri
della popolazione conoscendone la distribuzione a meno dei
parametri stessi; non parametriche se prescindono dalla
conoscenza della distribuzione della popolazione.
• Obiettivo dei test: come decidere se accettare o rifiutare
un’ipotesi statistica alla luce di un risultato campionario.
Esistono due ipotesi:
– H0 l’ipotesi nulla, cioè l’ipotesi che deve essere verificata
– H1 l’ipotesi alternativa la quale rappresenta, di fatto, l’ipotesi che
il ricercatore sta cercando di dimostrare.
Test per lo studio dell’associazione
tra variabili
• Si può incorrere in due tipologie di errore:
Possibili Risultati Verifica di Ipotesi
Stato di Natura
Legenda:
Risultato
(Probabilità)
Decisione
H0 Vera
Non
Rifiutare
H0
No errore
(1 - a )
Rifiutare
H0
Errore
Primo Tipo
(a)
H0 Falsa
Errore
Secondo Tipo
(β)
No Errore
(1-β)
Test per lo studio dell’associazione
tra variabili
• Errore di Primo Tipo
– Rifiutare un’ipotesi nulla vera
– Considerato un tipo di errore molto serio
La probabilità dell’errore di primo tipo è a
• Chiamato livello si significatività del test
• Fissato a priori dal ricercatore (i valori comuni sono 0.01, 0.05, 0.10)
• Errore di Secondo Tipo
– Non rifiutare un’ipotesi nulla falsa
La probabilità dell’errore di secondo tipo è β
• (1 – β) è definito come la potenza del test
Potenza = 1 – β = probabilità che un’ipotesi nulla falsa venga rifiutata
Lettura di un test statistico (1)
Esempio:
H0: b1= b2 = ....=bk = 0
1) Ipotesi
H1: almeno un bi≠0
2) Statistica test
3) p-value
Statistica F
Rappresenta la probabilità di
commettere l’errore di prima specie.
Può essere interpretato come la
probabilità che H0 sia “vera” in base al
valore osservato della statistica test
Lettura di un test statistico (2)
Fissato un livello di significatività a:
Se p-value piccolo (< a)
RIFIUTO H0
Altrimenti (>= a)
ACCETTO H0
Il p-value è il più piccolo valore di a per il quale H0 può essere rifiutata
PROC FREQ - Descrizione
La PROC FREQ permette di
• calcolare le distribuzioni di frequenza univariate
per variabili qualitative e quantitative discrete
• creare tabelle di contingenza a due o più
dimensioni per variabili qualitative e quantitative
discrete
• calcolare indici di dipendenza relativi a tabelle di
contingenza
Test chi-quadro – Indipendenza
statistica
• Si applica alle tabelle di contingenza a due
dimensioni
• Per testare l’hp di indipendenza statistica tra le
due variabili della tabella (ossia, la distribuzione di
X non è influenzata da Y e viceversa)
• Si calcola con la PROC FREQ (opzione CHISQ)
PROC FREQ – Sintassi generale
Calcolo dell’indice chi-quadro
proc freq data= dataset option(s);
tables variabile1 * variabile2 /option(s);
run;
OPTIONS:
• noprint non mostra i risultati nella finestra di output
• /missing considera anche i missing nel calcolo delle frequenze
• /chisq calcola l’indice chi-quadro e altre misure di
associazione basate sul chi-quadro
Esempio n°1- Test chi-quadro –
Indipendenza statistica
C’è indipendenza statistica tra le variabili sesso del
rispondente (SESSO) e possesso del computer
(COMPUTER)?
proc freq data=corso.telefonia;
table sesso * computer /chisq;
run;
Esempio n°1- Test chi-quadro –
Indipendenza statistica
Le frequenze della variabile COMPUTER subordinata a SESSO:
sesso=F
Cosa sono le frequenze
subordinate?
Frequency
Table of sesso by computer
Percent sesso(sesso) computer(computer)
Row Pct
0
1
16
84
Col Pct
F
6.78
35.59
16
84
28.57
46.67
40
96
M
16.95
40.68
29.41
70.59
71.43
53.33
56
180
Total
23.73
76.27
computer
computer
Percent
Frequency
Cumulative
Percent
16
100
29.41
70.59
Cumulative
Frequency
40
136
Cumulative
Percent
29.41
100
16
84
0
1
Total
sesso=M
100
42.37
computer
136
57.63
0
1
236
100
16
84
Cumulative
Frequency
16
100
computer
Percent
Frequency
40
96
Le frequenze della variabile di SESSO subordinata a COMPUTER:
computer = 0
sesso
sesso
Frequency
Percent
16
40
F
M
28.57
71.43
Cumulative
Frequency
16
56
Cumulative
Percent
28.57
100
Cumulative
Frequency
84
180
Cumulative
Percent
46.67
100
computer = 1
sesso
sesso
F
M
Frequency
Percent
84
96
46.67
53.33
Esempio n°1- Test chi-quadro –
Indipendenza statistica
Le frequenze subordinate (di SESSO subordinata a
COMPUTER e viceversa) sono diversedenota influenza di
ognuna delle due variabili sulla distribuzione dell’altra
(=dipendenza statistica)
Frequency
Table of sesso by computer
Percent sesso(sesso) computer(computer)
Row Pct
0
1
16
84
Col Pct
F
6.78
35.59
16
84
28.57
46.67
40
96
M
16.95
40.68
29.41
70.59
71.43
53.33
56
180
Total
23.73
76.27
Total
100
42.37
136
57.63
236
100
Esempio n°1- Test chi-quadro –
Indipendenza statistica
Possiamo concludere che le due variabili sono
statisticamente dipendenti?
Si considera la distribuzione χ², con un numero di gradi di libertà
pari a (k-1)(h-1), dove k è il numero di righe e h il numero di
colonne della tabella di contingenza. Qui:
H0 : indipendenza statistica tra X e Y
H1 : dipendenza statistica tra X e Y
Il p-value del test chi-quadro è basso (<0.05) rifiuto l’hp
nulla di indipendenza statistica  le due variabili sono
statisticamente dipendenti
Statistic
Chi-Square
Likelihood Ratio Chi-Square
Continuity Adj. Chi-Square
Mantel-Haenszel Chi-Square
Phi Coefficient
Contingency Coefficient
Cramer's V
DF
1
1
1
1
Value
5.7275
5.9139
5.0104
5.7032
-0.1558
0.1539
-0.1558
Prob
0.0167
0.015
0.0252
0.0169
Esempio n°2 - Test chi-quadro –
Indipendenza statistica
C’è indipendenza statistica tra le variabili SESSO e
MARCA?
proc freq data=corso.telefonia;
table sesso * marca /chisq;
run;
Esempio n°2 - Test chi-quadro –
Indipendenza statistica
Attenzione: molte celle con frequenze congiunte
assolute molto bassetest non molto affidabile
Frequency
Percent
Row Pct
sesso
Col Pct
F
Altro
M
Total
2
0.85
2
33.33
4
1.69
2.94
66.67
6
2.54
Lg
8
3.39
8
61.54
5
2.12
3.68
38.46
13
5.51
Motorola
19
8.05
19
36.54
33
13.98
24.26
63.46
52
22.03
Table of sesso by marca
marca
Nek
Nokia PalmOne Samsung Siemens
2
0.85
2
50
2
0.85
1.47
50
4
1.69
45
19.07
45
43.69
58
24.58
42.65
56.31
103
43.64
1
0.42
1
100
0
0
0
0
1
0.42
15
6.36
15
37.5
25
10.59
18.38
62.5
40
16.95
1
0.42
1
20
4
1.69
2.94
80
5
2.12
Total
Sony
Ericsson
7
2.97
7
58.33
5
2.12
3.68
41.67
12
5.08
100
42.37
136
57.63
236
100
Esempio n°2 - Test chi-quadro –
Indipendenza statistica
Il p-value del test chi-quadro è alto accetto l’hp di
indipendenza statistica  le due variabili sono
statisticamente indipendenti
Statistic
Chi-Square
Likelihood Ratio ChiSquare
Mantel-Haenszel ChiSquare
Phi Coefficient
Contingency Coefficient
DF
Value
8 7.0754
8 7.5018
Prob
0.5285
0.4836
1
0.9191
0.0103
0.1731
0.1706
0.1731
Cramer's V
WARNING: 44% of the cells have expected counts
less
than 5. Chi-Square may not be a valid test.
Test t – Indipendenza lineare
• Si applica a variabili quantitative
• Per testare l’hp di indipendenza lineare tra due
variabili (ossia, il coefficiente di correlazione lineare
tra X e Y è nullo)
• Si calcola con la PROC CORR
PROC CORR - Descrizione
La PROC CORR permette di
• calcolare la correlazione tra due o più variabili
quantitative
PROC CORR – Sintassi generale
Correlazione tra due o più variabili
proc corr data= dataset;
var variabile1 variabile2 … variabilen;
run;
PROC CORR - Esempio
Correlazione tra il numero medio di ore di
utilizzo del telefono cellulare e del fisso al
giorno.
proc corr data=corso.telefonia;
var cell_h fisso_h;
run;
Output PROC CORR - Esempio
20
c
e
15
l
l
_
10
h
5
1
2
3
f i sso_h
Coefficiente di correlazione
lineare ρ(X,Y): è un indice
relativo, assume valori
compresi tra -1 e 1. Se ρ >0
(ρ <0) la relazione tra X e Y
è lineare positiva (negativa),
se ρ =0 non c’è relazione
lineare.
4
5
PROC CORR - Esempio
Correlazione tra la durata media delle chiamate effettuate
[durata_chiamate_e] e:
• durata media delle chiamate ricevute
[durata_chiamate_r]
• numero medio di ore di utilizzo del telefono cellulare al giorno
[cell_h]
• numero medio di ore di utilizzo del telefono fisso al giorno
[fisso_h]
proc corr data=corso.telefonia;
var durata_chiamate_e durata_chiamate_r
cell_h fisso_h;
run;
Output PROC CORR - Esempio
d
80
u
r
a
60
t
a
_
40
c
h
i
20
a
m
0
0
20
40
60
d u r a t a _ c h i a ma t e _ e
80
Esempio n°1 - Test t –
Indipendenza lineare
C’è indipendenza lineare tra il numero medio ore
utilizzo cellulare al giorno(CELL_H ) e il numero
medio ore utilizzo telefono fisso al giorno
(FISSO_H)?
proc corr data=corso.telefonia;
var cell_h fisso_h;
run;
Esempio n°1 - Test t –
Indipendenza lineare
Il p-value del test t è basso rifiuto l’hp di
indipendenza lineare  esiste una relazione lineare tra
le due variabili, anche se non molto forte (il coefficiente
di correlazione lineare è non nullo ma ha valore non
molto elevato)
Esempio n°2 - Test t –
Indipendenza lineare
C’è indipendenza lineare tra il numero medio ore
utilizzo telefono fisso (FISSO_H ) e il numero
medio di email inviate al giorno (EMAIL_H)?
proc corr data=corso.telefonia;
var fisso_h email_h;
run;
Esempio n°2 - Test t –
Indipendenza lineare
Il p-value del test t è alto accetto l’hp di indipendenza
lineare  non esiste una relazione lineare tra le due
variabili
Test F – Indipendenza in media
• test per indagare la relazione esistente tra una variabile quantitativa Y e
una variabile qualitativa X, confrontando le distribuzioni di Y condizionate ai
valori assunti dalla variabile X
• la metodologia consiste nel verificare la significatività delle differenze tra le
medie aritmetiche della variabile continua dei gruppi di osservazioni
generati dalle modalità assunte dalla variabile qualitativa
(ANOVA : ANalysis Of Variance)
• il confronto tra le medie avviene tramite il test F, basato sulla
scomposizione della varianza
H0: μ1 = μ2 = … = μk (le medie sono tutte uguali tra loro )
H1: le μi non sono tutte uguali (esistono almeno due medie diverse tra loro)
Test F – Indipendenza in media
Devianza Totale
somma dei quadrati degli scarti di ogni
valore dalla media generale
Devianza tra i gruppi
somma dei quadrati degli scarti di ogni
media di gruppo dalla media generale
Devianza interna ai gruppi (o
entro i gruppi )
somma degli scarti al quadrato di ogni
valore dalla media del suo gruppo
gdl = n-1
(n = num. dati)
gdl = p-1
(p= num. gruppi)
gdl = n-p
Varianza tra
Varianza nei
(o entro)
F= VarTRA/ VarNEI
Significatività del test p-value :
- se il p-value del test F è basso (<α) le differenze riscontrate tra
le medie sono significativerifiuto l’ipotesi nullaposso
affermare l’esistenza di una relazione tra la variabile Y e la
variabile X.
PROC ANOVA – Sintassi generale
Sia Y una variabile quantitativa e X una
variabile qualitativa
PROC ANOVA DATA=dataset;
CLASS X;
MODEL Y=X;
MEANS X;
RUN;
Esempio (1/2)
C’è relazione tra la soddisfazione del cliente
(SODDISFAZIONE_GLOBALE) e l’operatore
telefonico da lui scelto (OPERATORE)?
PROC ANOVA DATA =corso.telefonia;
CLASS operatore;
MODEL soddisfazione_globale=operatore;
MEANS operatore;
RUN;
Esempio (2/2)
Output proc anova:
Source
Tra
Nei (Entro)
DF
Sum of Squares
Varianza
Mean Square F Value Pr > F
Model
3
8.9317803
2.9772601
Error
231
427.8086453
1.8519855
Corrected Total
234
436.7404255
R-Square
eta quadro
Devianza
Coeff Var
0.020451
Level of
operatore
Tim
Tre
Vodafone
Wind
1.61 0.1884
Root MSE
20.9571
N
55
12
153
15
soddisfazione_globale
Mean
1.360877
6.493617
soddisfazione_globale
Mean
Std Dev
6.16363636
1.33004645
6.41666667
1.31137217
6.62745098
1.29209313
6.4
2.06328448
Il p-value del test F è alto (>α)accetto l’hp nulla di indipendenza in media
non esiste una relazione di dipendenza in media tra le due variabili
Esercizi
1. Testare se le variabili area geografica e sesso
del data set DENTI sono statisticamente
indipendenti
2. Testare l’ipotesi di indipendenza lineare tra le
variabili consumo di dentifrici della marca A e
numero di contatti pubblicitari totali del data
set DENTI
3. Testare l’ipotesi di indipendenza in media tra
la variabile consumo di dentifrici della marca
A e area geografica e confrontarla con quella
tra consumo di dentifrici della marca A e
dimensione della città di residenza.