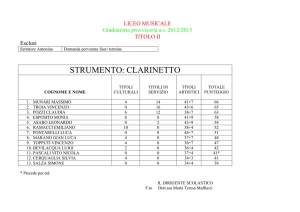
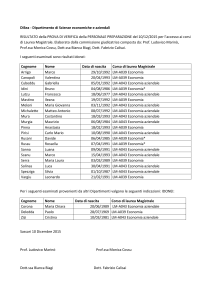
Presentazione 12.1
Algebra relazionale
Informatica Generale (Prof. Luca A. Ludovico)
Linguaggi di interrogazione per db relazionali
• Tipologia:
– Dichiarativi: specificano le proprietà del risultato
("che cosa")
– Procedurali: specificano le modalità di generazione
del risultato ("come")
• Rappresentanti più significativi:
– Algebra relazionale: procedurale
– SQL (Structured Query Language): dichiarativo
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Algebra relazionale
• Si basa su un insieme di operatori
–
–
–
definiti su relazioni
che producono relazioni
che possono essere composti
• Le relazioni sono insiemi.
• I risultati dell’applicazione di operatori su relazioni
(insiemi) debbono essere relazioni (insiemi).
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Operatori dell’algebra relazionale
• L'algebra relazionale ha 6 operatori di base e diversi
operatori derivati, che possono cioè essere definiti
come combinazione di operatori primitivi.
• Operatori fondamentali (di base):
1.
2.
3.
4.
5.
6.
operatori
operatori
operatori
operatori
operatori
operatori
binari di Unione
binari di Differenza
binari di Prodotto cartesiano
unari di Selezione
unari di Proiezione
unari di Ridenominazione
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Operatori dell’algebra relazionale
• I sei operatori precedenti sono fondamentali, perché
nessuno di essi può essere omesso senza perdere in
espressività.
• Operatori derivati (da quelli di base):
1.
2.
3.
operatore insiemistico binario di Intersezione
operatore di Join in varie forme (Theta-Join, Natural-Join, etc.)
operatore di Divisione
• Nel seguito indichiamo con r(X) la relazione r definita
sullo schema X. X è un insieme di attributi.
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Unione (teoria degli insiemi)
• Nella teoria degli insiemi, l'unione di due insiemi A e
B è data dall'insieme formato da tutti gli elementi
che appartengono all'insieme A o all'insieme B o a
entrambi.
• L'unione è una operazione binaria. Nell'algebra
booleana corrisponde all'operatore OR; in logica,
corrisponde alla disgiunzione.
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Unione (relazioni)
• Vincolo: avere tuple omogenee cioè definite sugli
stessi attributi.
• L'unione di due relazioni r1(X) e r2(X) definite sullo
stesso insieme di attributi X è indicata con
r1(X) r2(X).
• Il risultato è una relazione ancora su X contenente le
tuple che appartengono a r1 oppure a r2 oppure a
entrambe, senza ripetizioni delle eventuali tuple
ripetute.
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Unione
Solisti
Direttori
Nome
Cognome
Nome
Cognome
Uto
Ughi
Riccardo
Muti
Severino
Gazzelloni
Riccardo
Chailly
Salvatore
Accardo
Giuseppe
Sinopoli
Daniele
Gatti
Artisti = Solisti Direttori
Nome
Cognome
Riccardo
Muti
Riccardo
Chailly
Giuseppe
Sinopoli
Daniele
Gatti
Uto
Ughi
Severino
Gazzelloni
Salvatore
Accardo
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Intersezione (teoria degli insiemi)
• Nella teoria degli insiemi, l'intersezione di due
insiemi A e B è data dall'insieme formato da tutti gli
elementi che appartengono sia all'insieme A che
all'insieme B contemporaneamente.
• L'intersezione è una operazione binaria. Nell'Algebra
Booleana corrisponde all'operatore AND e, in logica,
alla congiunzione.
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Intersezione (relazioni)
• Vincolo: avere tuple omogenee cioè definite sugli
stessi attributi.
• L’intersezione di due relazioni r1(X) e r2(X) definite
sullo stesso insieme di attributi X è indicata con
r1(X) r2(X).
• Il risultato è una relazione ancora su X contenente
solo le tuple che appartengono sia a r1(X) sia a r2(X).
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Intersezione
Cantanti
Nome
Direttori
Cognome
Nome
Cognome
Luciano
Pavarotti
Riccardo
Muti
Josè
Carreras
Placido
Domingo
Placido
Domingo
Daniel
Harding
Daniele
Gatti
Cantanti Direttori
Nome
Placido
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Cognome
Domingo
Differenza (teoria degli insiemi)
• Nella teoria degli insiemi, dati due insiemi A e B, il
complemento di A rispetto a B (o l'insieme differenza
B – A), è formato dai soli elementi di B che non
appartengono ad A. Formalmente:
B – A = B / A = {x B x A}
• Si noti che l'insieme differenza B - A è un
sottoinsieme dell'insieme B.
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Differenza (relazioni)
• Vincolo: avere tuple omogenee cioè definite sugli
stessi attributi.
• Il complemento di r1(X) e r2(X) è indicato come
r2(X) − r1(X).
• Il risultato è una relazione su X contenente tutte le
tuple che appartengono a r2(X) e non appartengono a
r1(X).
• Si osservi che il secondo operando, r1(X), non è
necessariamente un sottoinsieme di r2(X).
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Differenza
Direttori in attività
Nome
Direttori italiani
Cognome
Nome
Cognome
Riccardo
Muti
Antonino
Votto
Daniel
Harding
Arturo
Toscanini
Claudio
Abbado
Giuseppe
Sinopoli
Daniel
Barenboim
Claudio
Abbado
Simon
Rattle
Daniele
Gatti
James
Levine
Riccardo
Muti
Daniele
Gatti
Direttori in attività - Direttori italiani
Nome
Cognome
Daniel
Harding
Daniel
Barenboim
Simon
Rattle
James
Levine
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Problema sugli insiemi
• Alle volte, alcune operazioni insiemistiche sarebbero
sensate ma sono rese impossibili dal fatto che gli
attributi presentano nomi differenti.
– Esempio: dati di locandina di Carmen
Autori
Cognome
Interpreti
Qualifica
Cognome
Ruolo
Bizet
compositore
Barenboim
direttore
Meilhac
librettista
Rachvelishvili
Carmen, mezzosoprano
Halévy
librettista
Kaufmann
Don José, tenore
Autori Interpreti ?
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Ridenominazione
• L'operatore unario di ridenominazione modifica lo
schema di una relazione, cambiando i nomi di uno o
più attributi.
• Utile per ottenere delle tuple omogenee quando non
lo sono (pur se il campo semantico della query lo è).
• Ciò che cambia sono i nomi degli attributi, mentre i
valori rimangono inalterati e vengono associati ai
nuovi attributi.
• Sintassi:
REN nuovo attrib. vecchio attrib. (operando)
r nuovo attrib. vecchio attrib. (operando)
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Ridenominazione
• Si “modifica lo schema” lasciando inalterata l'istanza
Autori
Interpreti
Cognome
Qualifica
Cognome
Ruolo
Bizet
compositore
Barenboim
direttore
Meilhac
librettista
Rachvelishvili
Carmen, mezzosoprano
Halévy
librettista
Kaufmann
Don José, tenore
REN
Qualifica Ruolo
(Interpreti)
Cognome
Schemi omogenei
Qualifica
Barenboim
direttore
Rachvelishvili
Carmen, mezzosoprano
Kaufmann
Don José, tenore
Ora è possibile calcolare Autori REN Qualifica Ruolo (Interpreti)
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Selezione
• È un operatore unario che restituisce come risultato
una relazione.
• Sintassi:
SEL condizione (operando)
s condizione (operando)
ove condizione è un’espressione booleana
• Semantica: produce un risultato che
– ha lo stesso schema dell'operando
– contiene un sottoinsieme delle ennuple dell'operando
– contiene solo le ennuple che soddisfano una data condizione,
complessa a piacere
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Esempi di selezione
Selezionare tutti gli studenti di nome “Paola”:
s NOME = “Paola” (studente)
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Esempi di selezione
Selezionare tutti gli studenti in cui l’istanza dell’attributo CITTA’ è
“Torino” o “Roma” e l’istanza dell’attributo C-DIP è diversa da “Log”
SEL ((CITTA= “Torino” OR CITTA= “Roma”) AND (NOT(C-DIP=“Log”))) (studente)
s((CITTA= “Torino” CITTA= “Roma”) C-DIP=“Log”))) (studente)
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Proiezione
• È un operatore unario che restituisce come risultato
una relazione.
• Sintassi:
PROJ lista attributi (operando)
p lista attributi (operando)
ove lista attributi è un sottoinsieme dello schema X.
• Semantica: produce un risultato che
– ha parte degli attributi dell'operando, ossia tutti quelli
elencati in lista attributi
– contiene ennuple cui contribuiscono tutte le ennuple
dell'operando
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Esempi di proiezione
Restituire una tabella avente come schema gli attributi NOME e
C-DIP e come istanza la restrizione delle tuple sugli attributi NOME
e C-DIP
p NOME, C-DIP (studente)
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Esempi di proiezione
Restituire una tabella avente come schema l’attributo C-DIP e come
istanza la restrizione delle tuple sull’attributo C-DIP
p C-DIP (studente)
Supponendo di fare un’operazione di proiezione solo sull’attributo C-DIP
della relazione studente, si verrebbero a creare dei duplicati, delle tuple
ripetute (ci sono infatti due studenti nel corso d’informatica).
Nei linguaggi formali la proiezione elimina automaticamente i duplicati.
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Cardinalità delle proiezioni
• Una proiezione:
– contiene al più tante ennuple quante l'operando
– può contenerne di meno, a causa di eliminazione di
duplicati
• Se X, insieme degli attributi su cui si effettua la
proiezione, è una superchiave di R, allora PROJX(R)
contiene esattamente tante ennuple quante R.
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Selezione e proiezione
• Sono due operatori "ortogonali“
– selezione: decomposizione orizzontale
– proiezione: decomposizione verticale
Proiezione
Selezione
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Esercizi
• Quali studenti (identificati dal solo nome) sono iscritti
al diploma di informatica?
• Quali studenti di Logistica (identificati dalla
matricola) non sono di Milano?
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Soluzioni
• Quali studenti (identificati dal solo nome) sono iscritti
al diploma di informatica?
p
Nome
sC-DIP=“Inf” (STUDENTE)
Nome
Carlo
Paola
• Quali studenti di Logistica non sono di Milano?
p
Matr
sC-DIP=“Log” ((Città=“Milano”))(STUDENTE)
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Matr
702
Esercizio
• Estrarre la matricola degli studenti che hanno preso
almeno un voto superiore a 28 e non sono mai scesi
sotto il 25.
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Soluzione
• Vengono sottratti a tutti gli studenti (identificati dalla
sola matricola) che hanno preso un voto maggiore o
uguale a 28 tutti quelli che hanno preso un voto
inferiore a 25.
pMatr sVoto>=28 (ESAME) - pMatr sVoto<25 (ESAME)
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Estrazione di informazioni dalle relazioni
• Combinando selezione e proiezione, è possibile
estrarre interessanti informazioni da una relazione.
• Non è ancora possibile però correlare informazioni
presenti in relazioni diverse.
• Il join è l'operatore dell'algebra relazionale che
permette di correlare dati in relazioni diverse.
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Prodotto cartesiano
• Il prodotto cartesiano di due relazioni R e S, indicato
con R x S, è una tabella (priva di nome) avente come
schema gli attributi di R e S e come istanza tutte le
possibili coppie di tuple di R e S.
Cantanti
Rappresentazioni
Nome
Cognome
Opera
Teatro
Luciano
Pavarotti
Tosca
Scala
Josè
Carreras
Aida
Metropolitan
Cantanti X Rappresentazioni
Nome
Cognome
Opera
Teatro
Luciano
Pavarotti
Tosca
Scala
Luciano
Pavarotti
Aida
Metropolitan
Josè
Carreras
Tosca
Scala
Josè
Carreras
Aida
Metropolitan
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Join
• Join è un operatore derivato dell’algebra relazionale,
e più precisamente si tratta di una particolare
selezione fatta sulla relazione ottenuta da un prodotto
cartesiano.
• Più formalmente ciò che produce il join è una tabella
(priva di nome) avente per schema la concatenazione
degli schemi di origine e per istanza le tuple ottenute
concatenando quelle tuple dei due schemi che
soddisfano un predicato.
• Sintassi: A JOIN
predicato
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
B oppure A predicato B
Join
• La sintassi del predicato di join è un’espressione
congiuntiva (ossia un AND) di predicati semplici:
ATTR1 op ATTR2
ove ATTR1 appartiene a TAB1, ATTR2 appartiene a
TAB2 e op è un operatore di confronto.
• Il join può essere classificato in due diversi tipi:
– equi-join: consente soli confronti di uguaglianza. Il predicato
va specificato.
– join naturale: equi-join di tutti gli attributi omonimi. Si
omette il predicato e si elimina la colonna ripetuta.
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Esempio di join
• Equi-join: STUDENTE STUDENTE.Matr = ESAME.Matr ESAME
è equivalente alla seguente espressione
s STUDENTE.Matr = ESAME.Matr (STUDENTE X ESAME)
• Join naturale: STUDENTE ESAME
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Esempio di join naturale
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Join completo, incompleto e vuoto
• Se tutte le tuple delle relazioni chiamate in causa
partecipano al join, si parla di join completo.
• Se alcune tuple dell’una o dell’altra relazione non vi
partecipano, si parla di join incompleto.
• Se il join non riesce a relazionare alcuna tupla della
prima relazione con alcun’altra della seconda
relazione, si parla di join vuoto.
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Join esterno
• Nel caso di join incompleto o vuoto, alcune ennuple
possono non contribuire al risultato in quanto la
colonna su cui opera il join non ha una controparte
nell’altra relazione.
• Il join esterno estende, con valori nulli, le ennuple
che verrebbero tagliate fuori da un join (interno).
Esiste in tre versioni:
– sinistro (JOINleft): mantiene tutte le ennuple del primo
operando, estendendole con valori nulli, se necessario
– destro (JOINright): ... del secondo operando ...
– completo (JOINfull): ... di entrambi gli operandi ...
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Osservazioni sulla cardinalità del join
• Siano R1(A,B), R2(B,C) due relazioni con alcuni
attributi in comune, identificati come insieme B.
• In generale, il join di R1 e R2 contiene un numero di
ennuple compreso fra zero ed il prodotto di |R1| e
|R2|: 0 ≤ |R1 JOIN R2| ≤ |R1| × |R2|
• Se il join coinvolge una chiave di R2 (ovvero, B è
chiave in R2), allora il numero di ennuple è compreso
fra zero e |R1|: 0 ≤ |R1 JOIN R2| ≤ |R1|
• Se il join coinvolge una chiave di R2 (ovvero, B è
chiave in R2) ed esiste un vincolo di integrità
referenziale fra B (in R1) e R2, allora il numero di
ennuple è pari a |R1|: |R1 JOIN R2| = |R1|
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Esercizio
• Estrarre il nome degli studenti che non hanno mai
preso meno di 28.
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Soluzione
• Nell’ultima parte della soluzione vengono trovate tutte le
matricole degli studenti che hanno preso un voto minore di 28.
• Queste matricole vengono sottratte alle matricole di tutti gli
studenti che hanno sostenuto esami. Rimangono quindi le
matricole degli studenti che non hanno mai preso un voto minore
di 28.
• Per trovare il nome di queste matricole viene fatto un join con la
tabella STUDENTE.
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Esercizio
• Estrarre il nome degli studenti che hanno sostenuto
“informatica” e “matematica” lo stesso giorno.
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1
Soluzione
•
•
•
•
Viene inizialmente fatto un join (seconda riga) tra la tabella ESAME e le tuple
della tabella CORSO che hanno come istanza dell’attributo Titolo la parola
“informatica”. Facendo cosi si ottiene una tabella che contiene tutti gli studenti
che hanno fatto l’esame di informatica (oltre a tutti gli attributi di ESAME e
CORSO).
Nell’ultima riga viene creata analogamente una tabella che contiene gli studenti
che hanno fatto matematica. Ne vengono proiettati gli attributi Matr e Data e
vengono ridenominati in MatrMat e DataMat. La relazione così ottenuta (formata
dai due attributi MatrMat, DataMat) viene posta in join con la tabella degli
studenti di informatica.
Viene posta la condizione di join: Matr = MatrMat e Data = DataMat in modo da
ottenere solo quegli studenti che hanno dato entrambi gli esami e nella stessa
data.
Il nome di questi studenti è però contenuto nella tabella STUDENTI, e quindi
viene fatto un ulteriore join (la prima riga) proprio con la tabella STUDENTI, per
ottenere i nomi degli studenti in questione.
Informatica Generale (Prof. Luca A. Ludovico)
Presentazione 12.1