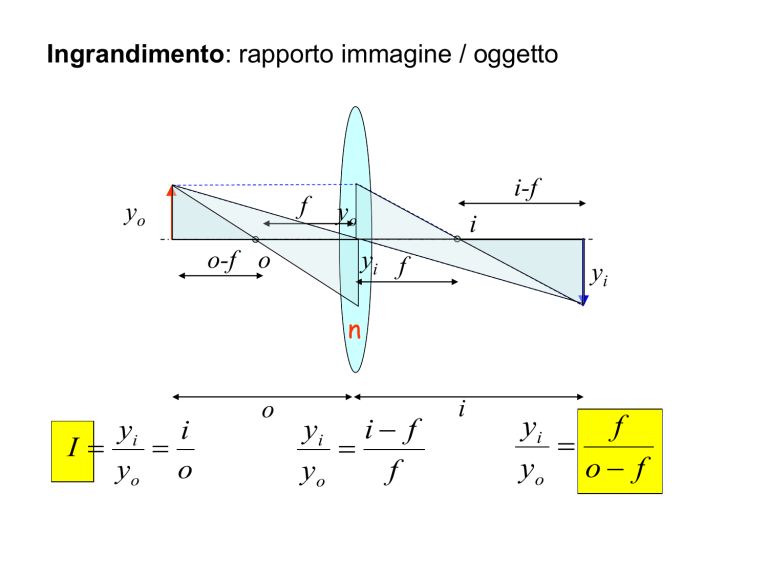
Ingrandimento: rapporto immagine / oggetto
f
yo
o-f o
i-f
yo
i
yi f
yi
n
yi
i
I
yo o
o
yi i f
yo
f
i
yi
f
yo o f
f
per o>f I
o f
I>1
vicino a f o-f ~ 0 I molto grande
Quindi, per ingrandire conviene mettersi poco prima del fuoco
per o > 2f
Ma attenzione…
2f
f
f
o-f > f
I<1
Se (per o>f) uso una lente più forte (fuoco minore),
per l’oggetto nella stessa posizione…
oggetto
1 1 1
o i f
immagine
fuoco
f
n
o
i
i si fa più vicina al fuoco e… l’immagine è più piccola
Se avvicino “troppo” (o
<f
1 1 1
o i f
=oltre il fuoco) …
immagine
…i
oggetto
< 0 = immagine virtuale
immagine
fuoco
f
n
i
o
i
Immagine virtuale
1 1 1
o i f
Se uso una lente più forte
(fuoco minore, ma sempre o<f) …
i si fa più lontana e … l’immagine è più grande
immagine
oggetto
fuoco
f
n
o
i
f
I
per o < f I < -1
o f
Se l’oggetto tende a zero I tende a -1
Se l’oggetto tende a f I tende a
-∞
Immagine all’infinito
n
Nota bene: ingrandimento negativo vuol dire solo immagine non capovolta
Lente d’ingrandimento: Ingrandimento angolare (o visuale)
tg yo / f d
I
tg
yo / d
f
yo
d 25 cm
Microscopio
l’immagine della prima lente (obiettivo) è l’oggetto della seconda (oculare) posto nel fuoco
Oculare
Obiettivo
Lunghezza di camera
D = i - fob
yo
fob
foc
yi yo'
fob
foc
∞
i f ob d
tg yo' / f oc yi d
Dd
I
I ob I oc
tg
yo / d
yo f oc
f ob f oc f ob f oc
Cioè: l’ingrandimento (angolare) di un microscopio è
il prodotto di quello dell’obiettivo e dell’oculare
(d 25 cm)
o ( f i)
Se i è fissa, allora lente (obiettivo) più forte …
i f
i f
30
oggetto
immagine
fuoco
n
o
25
20
f
o( f 6)
i
o ( f 20 )
15
10
…ingrandimento maggiore, ma …
… oggetto più vicino
1 1 1 i f
o f i i f
5
0
0
1
2
3
f
Ingrandimenti
maggiori
4
5
f
Oggetto prima del fuoco
Oggetto nel fuoco fasci paralleli
’ >
f minore
’
maggiore ingrandimento
&
angoli maggiori
Problema….
aberrazioni
minore
risoluzione
Qui stiamo uscendo
dall’ottica geometrica
Apertura Numerica
NA= n · sin
n
maggiore
risoluzione
Profondità
di campo
Contrasto
diaframma
diffrazione
minore
risoluzione
Profondità di campo
NA maggiore profondità di campo minore
Microscopi ottici
alti ingrandimenti NA grandi campioni piatti
Microscopi elettronici
gli NA usati sono molto piccoli (per evitare le
aberrazioni) quindi la profondità di campo è
estremamente elevata
Profondità di fuoco
profondità di campo riportata sul piano immagine
= Profondità di campo x (ingrandimento)2
Contrasto
Per vedere qualcosa in una immagine dobbiamo avere contrasto (C)
fra aree adiacenti del campione:
C
I s Ib
I
Ib
Ib
L’occhio umano non riesce ad apprezzare differenze di intensità
inferiori al 5-10% (utilità di acquisire immagini digitali da elaborare)
___________________________________________________
Due effetti del diaframma sul contrasto:
•Elimina dettagli (bordi sfumati) ( = peggioramento risoluzione)
•Elimina fondo diffuso
intensità
intensità
Is
Ib
Is
Ib
distanza
distanza
Strategie costruttive
Microscopia Ottica
Microscopia Elettronica
Possibilità di correzioni aberrazioni
Difficoltà correzione aberrazioni
Diaframmi solo
per il contrasto
Compromesso con
la risoluzione
Angoli grandi
piccola
profondità
di campo
Massima risoluzione consentita dalla
lunghezze d’onda
Diaframmi solo per contrasto
compromesso con la risoluzione
Diaframmi
grande
profondità
di campo
Perdita di risoluzione
Ma le piccolissime lunghezze d’onda
consentono comunque grandi
risoluzioni
Diffrazione da una fenditura
(piccola, cioè non sia d>>λ )
d sinθ
Sorgente
puntiforme
all’infinito
d
θ
θ
se qui d sinθ=λ
θ
qui è λ/2
Interferenza distruttiva
Primo minimo a sin θ1 = λ/d
Immagine
della
sorgente
Se la fenditura è circolare
2θ1 rappresenta il
diametro angolare dell’immagine
di un punto luminoso all’infinito data da
un sistema ottico (esente da
aberrazioni) con diametro di apertura d
sin 1 1.22
d
2θ1
Il risultato è indipendente dalla posizione della lente.
Non cambia neanche se il diaframma si trova dopo la lente.
Comunque sia prodotta la limitazione del fascio, se alla formazione
dell’immagine reale concorre un fascio che ha larghezza finita in
corrispondenza dell’obiettivo, l’immagine di un punto è una figura di
diffrazione di questo tipo.
•
Una lente di dimensione finita si comporta come un diaframma (non fa
passare luce per angoli maggiori della sua dimensione)
Airy disk
Potere risolutivo R
Il primo minimo della
curva blu è esattamente
sul massimo della curva
rossa
criterio di Rayleigh
la minima distanza tra i centri
dei dischi di diffrazione di due
punti affinchè questi siano
distinguibili è uguale al loro
raggio
Il potere risolutivo (o
separatore) R è l’inverso
dell’angolo minimo sotto il quale
due punti immagine devono
apparire all’obiettivo affinché
essi siano distinguibili
R ~ d/(1.22 λ)
Vogliamo passare dal piano immagine a quello oggetto.
Se P’Q’ è la distanza minima tra i due punti immagine,
quanto sono distanti P e Q?
Qual è cioè la distanza minima risolvibile rmin.
Differenza di
cammino
1.22λ
B
Q
rmin
θ1 1.22λ/d
P
P’
Q’
A
Distanza minima risolvibile rmin
B
Se prevediamo che il mezzo in cui
viaggiano i raggi non sia l’aria
(lenti ottiche a immersione)
al posto di λ dobbiamo mettere λ/n
n indice di rifrazione del mezzo tra
l’oggetto e la lente
Q
rmin 0.61
n sin
P
Apertura Numerica (NA)
AQ – BQ ~ 1.22 λ
2 PQ sin ~ 1.22 λ
rmin = PQ ~ 1.22 λ/2sin
A
Attenzione: spesso, soprattutto in
microscopia elettronica, si parla
genericamente di risoluzione o
anche di potere risolutore per indicare
la minima distanza risolvibile












