FORMULARIO: disequazioni irrazionali

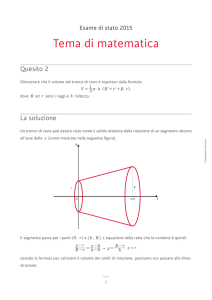
FORMULARIO: disequazioni irrazionali
le soluzioni si ottengono imponendo e
risolvendo i due sistemi
le soluzioni si ottengono imponendo e
risolvendo il sistema
FORMULARIO: logaritmi
» definizione:
» cambiamento di base:
,
,
» proprietà:
,
,
,
,
Triangoli
» Calcolo dell'area:
formula di Erone
» Lunghezza delle mediane:
,,
» Teorema della mediana:
» Bisettrici:
,,
» Teorema della bisettrice dell'angolo interno:
» Teorema della bisettrice dell'angolo esterno:
(se i segmenti esistono)
» Raggio della circonferenza circoscritta:
,
,
,
» Raggio della circonferenza inscritta:
2p=a+b+c
,
,
,
,
» Altezze:
,
» Teorema dei seni (o di Eulero)
In un triangolo è costante il rapporto tra la misura di un lato e il seno dell'angolo opposto:
» Teorema della corda
In un triangolo il rapporto tra la misura di un lato e il seno dell'angolo opposto è uguale al diametro
della circonferenza circoscritta:
= 2r
» Teorema del coseno (o di Carnot)
In un triangolo il quadrato di un lato è uguale alla somma dei quadrati degli altri due diminuita del
prodotto di questi due lati per il coseno dell'angolo fra essi compreso:
,
,
,
,
» Formule di Briggs:
,
,
.
» Teorema di Pitagora:
In un triangolo rettangolo il quadrato costruito sull'ipotenusa è equivalente alla somma dei quadrati
costruiti sui due cateti.
» Primo teorema di Euclide:
In un triangolo rettangolo il quadrato costruito su un cateto è equivalente al rettangolo che ha per
dimensioni la sua proiezione sull'ipotenusa e l'ipotenusa stessa.
;
» Secondo teorema di Euclide:
In un triangolo rettangolo l'altezza è media proporzionale tra le proiezioni dei due cateti
sull'ipotenusa.
» Proprietà della mediana:
» Calcolo dell'area:
,
» Misura dell'altezza noti i lati:
» 1° teorema sui triangoli rettangoli:
In un triangolo rettangolo la misura di un cateto è uguale al prodotto dell'ipotenusa per il seno
dell'angolo opposto o per il coseno dell'angolo adiacente
,
» 2° teorema sui triangoli rettangoli:
In un triangolo rettangolo la misura di un cateto è uguale al prodotto dell'altro cateto per la tangente
dell'angolo opposto o per la cotangente dell'angolo adiacente
,
Cerchio
LEGENDA
Lunghezza della circonferenza:
Raggio = r
Area del cerchio:
Lunghezza dell'arco:
Area del settore circolare:
Area del semicerchio:
Area del quadrante:
Area della corona circolare:
Area del segmento circolare: si trova
come differenza fra l'area di un settore
e l'area di un triangolo.
» Teorema della corda: (vedi anche il
terorema dei seni)
dove α è uno qualsiasi degli angoli alla
circonferenza inscritti nell'arco
maggiore AB .
» Calcolo dell’area quadrilatero
Qui sopra puoi sperimentare il Teorema della corda,
variando l'ampiezza dell'angolo α
Solidi
Le figure geometriche solide possono essere suddivise in due gruppi:
quelli la cui superficie è formata da soli poligoni detti poliedri, e quelli la cui superficie è curva
detti solidi rotondi.
Un poliedro è un solido limitato da più poligoni posti su piani diversi e tali che ogni lato è
comune a due soli di essi.
Tra le facce gli spigoli e i vertici di un poligono sussiste la relazione di Eulero: f + v = s + 2
I poliedri possono essere suddivisi in poliedri regolari, prismi e piramidi, come è raffigurato
nello schema.
Un poliedro si dice regolare se tutte le sue facce sono poligoni regolari uguali fra loro e tutti i
diedri e gli angoloidi sono uguali fra loro.
I poliedri regolari che si possono costruire sono 5, noti anche come solidi platonici.
poliedro
Pol.
regolare
N° N°
fac vert
ce
ici
N°
spigo
li
N° spig.
vertice
Tetraedro
triangolo
4
4
6
3
Cubo o
Esaedro
quadrato
6
8
12
3
triangolo
8
6
12
4
Dodecaedro pentagono 12
20
30
3
Icosaedro
12
30
5
Ottaedro
triangolo
20
LEGENDA
= altezza
= spigolo
= diagonale
= Area della superficie totale
= Volume
altezza
diagonal
e
Area della
superficie
Volume
Prisma
diagonale
superficie laterale
superficie totale
prisma retto
parallelepipedo retto
parallelepipedo rettangolo
cubo
Prismi
Il prisma è un poliedro limitato da due poligoni uguali e paralleli (basi) e da tanti
parallelogrammi (facce laterali) quanti sono i lati del poligono di base.
prisma obliquo: se tutte le facce laterali sono parallelogrammi e l’altezza non
coincide con uno degli spigoli
prisma retto: se tutte le facce laterali sono perpendicolari alle basi e l’altezza
coincide con uno degli spigoli
prisma regolare: se è retto e le basi sono poligoni regolari (le facce laterali sono
rettangoli uguali fra loro).
Prismi particolari
Parallelepipedo
Un parallelepipedo è un prisma le cui basi sono dei parallelogrammi.
Un parallelepipedo può essere:
retto: se tutte le sue facce sono perpendicolari alle basi (le facce sono dei rettangoli e
le basi dei parallelogrammi)
rettangolo: se è retto e le sue basi sono dei rettangoli (tutte e sei le facce sono
rettangoli uguali e paralleli a due a due)
Cubo
Il cubo è un parallelepipedo rettangolo con le tre dimensioni uguali tra loro.
Il cubo è un poliedro regolare limitato da sei facce quadrate (esaedro).
superficie laterale
piramide qualsiasi
piramide retta
tronco di piramide
superficie totale
Volume
volume
Piramide
La piramide è un poliedro limitato da un poligono qualsiasi e da tanti triangoli quanti sono i lati di questo poligono, aventi tutti
un vertice in comune.
LEGENDA
V vertice
ABCDEF base (poligono di base)
VAB faccia laterale (triangolo)
VH altezza (distanza tra il vertice e la base)
VM apotema
H piede dell’altezza
VB spigolo laterale
AB spigolo di base
Una piramide si dice retta se il poligono di base è circoscrittibile a una circonferenza e il piede
dell’altezza coincide con il centro di questa circonferenza.
L’apotema di una piramide retta è l’altezza di una delle sue facce.
Una piramide si dice regolare se è retta ed il poligono di base è un poligono regolare.
Tronco di piramide
Tagliando una piramide con un piano parallelo alla base si ottengono due solidi: uno è ancora
una piramide , l’altro è un tronco di piramide. I due poligoni che lo delimitano costituiscono
le basi del tronco di piramide, e le facce laterali sono dei trapezi. La distanza tra le basi è
l’altezza del solido.
Un tronco di piramide si dice retto se è stato ottenuto da una piramide retta.
Un tronco di piramide si dice regolare se è stato ottenuto da una piramide regolare.
Le facce laterali di un tronco di piramide regolare sono tutti trapezi isosceli congruenti.
L’altezza di uno qualsiasi di questi trapezi è l’apotema del tronco di piramide.
Solidi di rotazione
Sono solidi ottenuti dalla rotazione di una figura piana intorno ad una retta (asse di rotazione).
superficie laterale
superficie totale
volume
Cilindro
Cono
Tronco di cono
superficie sferica
Sfera
Cilindro
Il cilindro è un solido ottenuto dalla rotazione completa di un rettangolo intorno ad un
suo lato.
Cilindro equilatero
È un cilindro in cui l’altezza è lunga quanto il diametro della base.
L’area della superficie laterale di un cilindro si ottiene moltiplicando la lunghezza della
circonferenza di base per la misura dell’altezza:
L’area della superficie totale di un cilindro si ottiene sommando la superficie laterale e
l’area delle due basi:
Il volume di un cilindro si ottiene moltiplicando l’area di base per la misura dell’altezza:
Cono
Il cono è un solido ottenuto dalla rotazione di un triangolo intorno ad un suo cateto.
Cono equilatero
È un cono in cui l’apotema è lungo quanto il diametro della base.
L’area della superficie laterale di un cono si ottiene moltiplicando la lunghezza della
circonferenza di base per la misura dell’apotema e dividendo tale prodotto per due:
L’area della superficie totale di un cono si ottiene sommando la superficie laterale e
l’area della base:
Proprietà. Il cono è equivalente a un terzo di un cilindro avente base ed altezza
congruenti rispettivamente alla base e all’altezza del cono.
Il volume di un cono si ottiene moltiplicando l’area di base per la misura dell’altezza e
dividendo tale prodotto per tre:
volume
Tronco di cono
Consideriamo un cono e tagliamolo con un piano parallelo al piano della base: otteniamo
due figure, una è ancora un cono, l’altra è un tronco di cono.
Il tronco di cono è un solido attenuto dalla rotazione di un trapezio rettangolo attorno al
lato perpendicolare alle basi.
Proprietà. La superficie laterale di un tronco di cono è equivalente a un trapezio avente
per basi le due circonferenze di base del tronco e per altezza il suo apotema.
L’area della superficie laterale di un tronco di cono si ottiene moltiplicando la somma
delle misure delle lunghezze delle due circonferenze di base per la misura dell’apotema e
dividendo tale prodotto per due:
L’area della superficie totale di un cono si ottiene sommando la superficie laterale e
l’area delle due basi:
Proprietà. Per il principio di Cavalieri, un tronco di cono e un tronco di piramide aventi
basi equivalenti e altezze congruenti sono equivalenti.
Il volume di un cono si ottiene moltiplicando ,l’area di una base più l’altra base + la
radice quadrata del prodotto delle due basi, per la misura dell’altezza e dividendo tale
prodotto per tre:
Sfera e superficie sferica
La sfera è un solido ottenuto dalla rotazione completa di un semicerchio attorno al
proprio diametro, il raggio e il centro del semicerchio sono il raggio e il centro della sfera.
La superficie sferica è l’insieme di tutti e solo i punti dello spazio che hanno la stessa
distanza da un punto interno detto centro.
Proprietà. La superficie sferica è equivalente alla superficie laterale del cilindro equilatero
circoscritto ad essa.
L’area della superficie sferica si ottiene moltiplicando per quattro l’area del suo cerchio
massimo:
Proprietà. Una sfera è equivalente a un cono avente per altezza il raggio della sfera e per
raggio di base il diametro della sfera.
Il volume della sfera si ottiene moltiplicando
per il cubo del suo raggio: