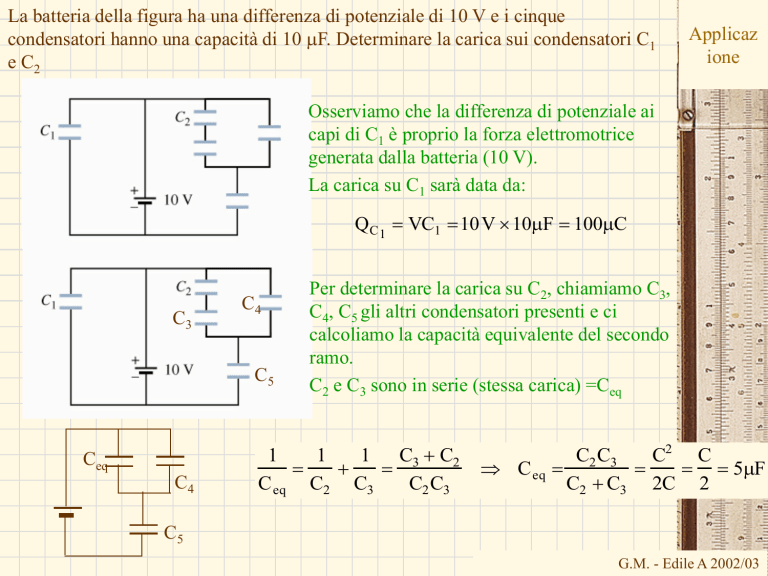
La batteria della figura ha una differenza di potenziale di 10 V e i cinque
condensatori hanno una capacità di 10 mF. Determinare la carica sui condensatori C1
e C2
Applicaz
ione
Osserviamo che la differenza di potenziale ai
capi di C1 è proprio la forza elettromotrice
generata dalla batteria (10 V).
La carica su C1 sarà data da:
QC 1 VC1 10V 10mF 100mC
C3
C4
C5
Ceq
C4
Per determinare la carica su C2, chiamiamo C3,
C4, C5 gli altri condensatori presenti e ci
calcoliamo la capacità equivalente del secondo
ramo.
C2 e C3 sono in serie (stessa carica) =Ceq
1
1
1 C3 C2
C eq C2 C3
C2 C3
C eq
C2 C3
C2 C
5mF
C2 C3 2C 2
C5
G.M. - Edile A 2002/03
La batteria della figura ha una differenza di potenziale di 10 V e i cinque
condensatori hanno una capacità di 10 mF. Determinare la carica sui condensatori C1
e C2
Ceq
C4
C5
Ceq e C4 sono in parallelo (stessa differenza di potenziale ai
loro capi) =C’eq
C' eq C eq C 4 5mF 10mF 15mF
C’eq e C5 sono in serie (stessa carica) =C’’eq
C"eq
C’eq
C' eq C5
C' eq C 5
La carica su C’’eq
C5
Applicaz
ione
15 10
mF 6mF
25
QC"eq VC"eq 10V 6mF 60mC
Questa è anche la carica su C’eq e C5 perché sono in serie.
QC5 60mC
La tensione ai capi di C’eq è data da:
C’’eq
La carica su C4
VC' eq
Q
60mC
4V
C' eq 15mF
QC 4 VC' eq C4 4V 10mF 40mC
La carica su Ceq e quindi su C2
QCeq QC2 VC' eq Ceq G.M.
4V -Edile
5mFA2002/03
20mC
Un condensatori a piatti piani paralleli di area A viene riempito con due dielettrici
come mostrato in figura.
Si dimostri che la capacità è data dall’espressione
A)
B)
C o
Applicaz
ione
A r1 r 2
d 2
A
C 2 o r1 r 2
d r1 r2
Prima di passare alla soluzione del
problema guardiamo più da vicino
il comportamento dei dielettrici in
un campo magnetico.
G.M. - Edile A 2002/03
I dielettrici
•
•
•
•
In contrapposizione ai conduttori, i
dielettrici non hanno cariche capaci
di muoversi su tutto il volume da
essi occupati.
Ciononostante anche i dielettrici
sono costituiti da atomi e da
molecole
quindi da particelle come elettroni e
protoni che trasportano carica
elettrica.
Queste particelle nei dielettrici sono
obbligati a mantenere delle
posizioni fisse: possono solo
oscillare rispetto alla loro posizione
di equilibrio
•
In ogni caso i dielettrici, essendo
costituiti da oggetti che trasportano
cariche elettriche, subiscono
l’influenza del campo elettrico
•
Si distinguono in
– Dielettrici polari
– Dielettrici non polari
G.M. - Edile A 2002/03
Dielettrici polari
•
Tipica molecola polare quella dell’acqua
– Nella figura precedente sono disegnate due molecole di
acqua
• La sfera rosa rappresenta l’ossigeno (negativo)
• Quella avio l’idrogeno (positivo)
• Sono mostrati i legami tra l’idrogeno e l’ossigeno e quello
tra l’ossigeno di un molecola e l’idrogeno dell’altra (legame
molecolare)
•
•
•
•
Il centro di “carica” della carica negativa non coincide
con quello della carica positiva
Una molecola polare posta in un campo elettrico tende
ad orientarsi in accordo al campo elettrico applicato
Gli urti tra le molecole, dovuti all’agitazione termica,
disturbano l’allineamento.
L’allineamento sarà comunque tanto maggiore quanto
maggiore è il campo elettrico
G.M. - Edile A 2002/03
Dielettrici non polari
Nei dielettrici non polari il centro di “carica” della carica positiva coincide, in
assenza di campo elettrico, con quello della carica negativa, fig. a).
La presenza del campo elettrico tenderà a spostare gli elettroni dell’atomo da una
parte e il nucleo dall’altra. I due centri di “carica” non saranno più coincidenti (fig.
b)
G.M. - Edile A 2002/03
Riduzione del campo elettrico per effetto
del dielettrico
•
•
•
Consideriamo un condensatore piano inizialmente
nel vuoto, fig a
Introduciamo poi un dielettrico, fig b:esso si
polarizza
L’effetto della diversa localizzazione delle cariche
positive e negative in ciascuna atomo o molecola
– Si compensa all’interno del dielettrico
– Crea delle distribuzioni di carica sulle superficie del
dielettrico
• di segno opposto rispetta alla carica distribuita sulle
armatore del condensatore nel vuoto
• Il cui effetto è quello di far diminuire il campo
elettrico all’interno del dielettrico rispetto al valore
del campo elettrico nel vuoto
•
Si definisce costante dielettrica relativa il rapporto
tra il campo elettrico nel vuoto e quello in
presenza di dielettrico a parità di carica sulle
armature
E
Eo
r
A
C
r o
Per il condensatore piano
d
G.M. - Edile A 2002/03
G.M. - Edile A 2002/03
Un condensatori a piatti piani paralleli di area A viene riempito con due dielettrici
come mostrato in figura.
Si dimostri che la capacità è data dall’espressione
Applicaz
ione
Il caso A può essere considerato come due condensatori piani in parallelo di armatura
di area A/2, spessore d, e costanti dielettriche relative r1 ed r2.
C1 r1 o
A
C 2 r 2 o
A
2
d
2
Ceq C1 C2 o
A
2
d
r1 r2
d
G.M. - Edile A 2002/03
Un condensatori a piatti piani paralleli di area A viene riempito con due dielettrici
come mostrato in figura.
Applicaz
ione
Nel caso B, tenendo conto che, sulla base della simmetria del dispositivo, si deduce
che le superficie equipotenziali sono delle superfici parallele alle armature.
Pertanto la superficie di separazione tra i due dielettrici è equipotenziale e può essere
sostituita da una sottile lastra metallica.
Ne segue che l’intero condensatore può essere considerato come due condensatori
piani in serie aventi armatura di area A, spessore d/2, e costanti dielettriche relative
A
A
A
r1 ed r2.
C1 r1 o d
r1 o d r2 o d
C1C2
A
r1 r 2
2
2
2
C
eq
od
A
A
A
C1 C2
2 r1 r2
C
2
r2 o d
2
r1 o d
2
r2 o d
2
G.M. - Edile A 2002/03
Una corrente di 5 A scorre in una resistenza di 10 W per 4.0 min.
Quanti a) coulomb e quanti b) elettroni passano attraverso una qualsiasi sezione
trasversale della resistenza in questo intervallo di tempo?
•
•
•
•
Dalla definizione di corrente elettrica
Dove dq è la carica che attraversa una sezione del
conduttore nell’intervallo di tempo dt
si ottiene cheLa carica Q che attraversa una particolare
seziona del conduttore
Per i costante
t
t
Q
0
i
Q
Applicaz
ione
dq
dt
t
t
0
0
dq idt
idt i dt it 0 it
t
0
t 4min 4 60s 240s
Q it 5A 240s 1200C
•
•
Ogni elettroni ha una carica di 1.60x10-19C
Il numero n di elettroni transitati in 4 min attraverso
una sezione del conduttore sarà
n
Q
1200
21
7.5
10
elettroni
19
e 1.60 10
G.M. - Edile A 2002/03
Una corrente di 5 A scorre in una resistenza di 10 W per 4.0 min.
Qual è la caduta di potenziale ai capi della resistenza?
Qual è l’energia dissipata, in kWh, nella resistenza per effetto joule in 4 min?
Applicaz
ione
V Ri 10W 5A 50V
•
Per la legge di Ohm
•
La potenza dissipata per effetto joule è
P Ri 10W 25A 250W
•
L’energia dissipata in 4 min è
E Pt 250W 240s 60kJ
•
Un kWh è l’energia sviluppata da una potenza di 1kW in
un’ora (3600 s) 1kWh=3600kJ
•
Esprimendo l’energia dissipata sulla resistenza in 4
min in kWh si ottiene
2
E 60kJ 60
2
kWh
0.0167kWh
3600
G.M. - Edile A 2002/03
Un filo di nichlecromo (una lega di nichel-cromo-ferro comunemente usata per le
resistenze da riscaldamento) è lungo 1.0 m ed ha una sezione di area pari ad 1.0
mm2.
Esso è percorso da una corrente di 4.0 A quando viene applicata una differenza di
potenziale di 2.0 V ai suoi capi. Si calcoli la conducibilità s del materiale.
•
Calcoliamo la resistenza attraverso la legge di Ohm
•
La resistenza è legata alla geometria del conduttore e
alla sua conducibilità dalla relazione
– In cui r è la resistività del materiale
– e s la sua conducibilità (s1/r
•
La conducibilità s sarà data da:
s
R
Applicaz
ione
ddp V 2.0V
0.50W
i
i 4.0A
R r
S
1
sS
1
1.0m
6 1 1
6
2 2 10 W m
R S 0.50W 1.0 10 m
G.M. - Edile A 2002/03
Resistività di alcuni materiali
a) lega appositamente
progettata per avere bassi
valori di a
b) silicio drogato con atomi
di fosforo fino ad ottenere
una densità di portatori di
1023 m-3
c) silicio drogato con atomi
di aluminio fino ad ottenere
una densità di portatori di
1023 m-3
G.M. - Edile A 2002/03
Una comune lampadina per lampeggiatore viene alimentata, in condizioni operative
da una tensione di 2.9 V e una corrente 0.30 A. Se la resistenza del filamento alla
temperatura ambiente (20°C) è pari a 1.1 W, qual è la temperatura del filamento
quando la lampadina viene accesa? Il filamento è fatto di tungsteno.
r ro 1 aT To
•
La resistività di un materiale varia in accordo alla legge
•
Dove a è il coefficiente termico della resistività per il
R r
tungsteno a=4.5x10-3 K-1
S
Se la geometria del filamento resta costa costante con la
temperatura, allora anche la resistenza del filamento
varia con la stessa legge
R R o 1 aT To
•
•
Dove R è la resistenza alla temperatura T ed Ro è la
resistenza alla temperatura ambiente To.
•
•
la resistenza alla temperatura ambiente Ro è 1.1 W
La resistenza alla temperatura T sarà:
•
La temperatura di esercizio del filamento sarà:
T
R
Applicaz
ione
V
2.9V
9.67W
i 0.30A
R Ro
9.67W 1.1W
To
3 1 20C 1.731 20 1750C
R oa
1.1W 4.5 10 K
G.M. - Edile A 2002/03
Una stufa elettrica della potenza di 1250 W viene costruita per essere alimentata alla
tensione di 220 V
a) quale sarà la corrente nella stufa?
b) qual è la resistenza della spira riscaldante
a) quanta energia termica viene prodotta in un’ora dalla stufa?
•
P Vi
La potenza dissipata quando una corrente i attraversa
una ddp pari a V è data da
i
•
•
P 1250W
5.68A
V
220V
Attraverso la legge di Ohm ricaviamo la resistenza della
spira riscaldante
V Ri
R
L’energia termica prodotta in un’ora dalla stufa la
otteniamo dalla definizione di potenza
P
E
t
Applicaz
ione
V 220V
38.7W
i 5.68A
E Pt 1250W 3600s 4.5x10 J 1.25kWh
6
G.M. - Edile A 2002/03
Qual è la resistenza equivalente della rete illustrata?
Qual è la corrente in ciascuna resistenza?
Si ponga R1=100 W, R2=R3=50W, R4=75W, fem=6.0V
•
Applicaz
ione
Ai capi di R2, R3 e R4 c’è la stessa differenza di
potenziale
– queste resistenze sono in parallelo
•
La resistenza equivalente sarà
1
1
1
1
R R R 2 R4 R 3R 4
3 4
R R2 R3 R4
R 2R 3R 4
R
•
R2 R3 R4
50 50 75
18.75W
R 3R 4 R 2R 4 R 2R 3 50 75 50 75 50 50
La corrente in R1
i1
fem
6.0
0.050A
R1 R 100 18.75
i R 0.050 18.75
i2 i3 1
0.019A
R2
50
i4
i1R 0.050 18.75
0.013A
R4
75
G.M. - Edile A 2002/03












